奇异摄动系统的周期振荡
2022-07-14沈建和
赵 亮,沈建和
(1.福建师范大学数学与统计学院,福建 福州 350117;2.广西财经学院信息与统计学院,广西 南宁 530003)
两尺度奇异摄动系统的标准形式如下:
(1)
其中x∈Rn和y∈Rm为状态变量,0<ε≪1为摄动参数,λ∈Rl为分支参数,f和g关于其变量充分光滑.引入快尺度t=τ/ε后,可得慢系统(1)对应的快系统,
(2)
显然,当ε≠0时,系统(1)和(2)拓扑等价.在式(1)和式(2)中令ε=0,可分别得退化系统
(3)
和层系统
(4)
其中称
Cλ={(x,y,λ)|f(x,y,λ,0)=0}
为临界流形,它是层系统(4)的所有平衡点的集合.
Fenichel几何奇异摄动理论[1](简称GSPT)是研究奇异摄动系统的主要工具之一,其基本思想是:首先进行快慢分离,获得维数较低的层系统(快-极限系统)和退化系统(慢-极限系统);然后通过分析层系统和退化系统的动力学来获得整个奇异摄动系统(1)/(2)的动力学.然而,GSPT的前提是临界流形的法向双曲性.在法向非双曲点附近,GSPT不再适用.根据奇异摄动问题的流经过法向非双曲点附近时的分支行为,在通有情况下非双曲点可分为鸭点和跳跃点. 鸭点和跳跃点的存在,是奇异摄动系统产生奇异闭轨的必要条件.奇异闭轨经扰动可产生张弛振荡(含鸭型).张弛振荡的产生,通常与鸭爆炸紧密相关. 鸭爆炸是指在某临界参数的指数小范围内,由Hopf分支产生小振幅极限环经鸭环和最大鸭迅速过渡到张弛振荡的连续分支过程[2-4].至今,关于奇异摄动系统周期振荡的研究已有许多工作.
关于平面奇异摄动系统的周期振荡和鸭爆炸现象,Zhang等[5]研究了带Holling-III功能反应函数的Leslie-Gower奇异摄动捕食-食饵系统,用GSPT和鸭理论证明了张弛振荡、鸭环和同宿环的存在性以及鸭爆炸现象;通过计算慢散度积分,证明了系统鸭环的环性最多为2.Ai等[6]利用Poincaré-Bendixson定理和entry-exit函数,证明了张弛振荡的存在性、全局唯一性和轨道稳定性.Chen等[7]研究了一类具有Sigmoid功能反应函数的捕食-食饵系统,借助GSPT和定性理论,证明了系统连续出现两次鸭爆炸的现象.Chen等[8]研究了Tyson-Hong-Thron-Novak模型,利用GSPT给出了鸭爆炸、张弛振荡以及同异宿轨的存在性.更多的工作可见文[9-18].
关于三维及以上奇异摄动系统的周期振荡,至今亦有一些工作.Liu等[19]研究了两个捕食者竞争一个食饵的三维奇异摄动系统,通过建立适当的Poincaré映射,证明了三维相空间中稳定张弛振荡的存在性.Shen等[20]研究了一类具有演化效应的四维奇异摄动捕食-食饵模型,借助GSPT和entry-exit函数,证明了四维相空间中张弛振荡的存在性.Hsu等[21]通过对entry-exit函数的新的推广,给出了一般高维奇异摄动系统有关张弛振荡存在性和稳定性的判据.Sewalt等[22]研究了一类水-植被相互耦合的奇异摄动生态模型,结合GSPT和Melnikov方法,证明了四维相空间中脉冲周期轨道的存在性.
实际上,关于奇异摄动系统的周期振荡,除了张弛振荡之外,三维及以上相空间还可以存在诸如混合模式振荡(Mixed-mode Oscillations,MMOs) 等更为复杂的周期振动形式.MMOs是奇异摄动系统中小振幅振动(SAOs)和大振幅振动(LAOs)交替的一种复杂的周期振荡,它只能存在于三维及以上的奇异摄动系统,即系统(1)中的维数满足n+m≥3.至今,有关两尺度奇异摄动系统的MMOs,已有许多的工作,可见文[23-32].
以上所提的工作,均只涉及两尺度奇异摄动系统. 三尺度动力系统,只能存在于三维及以上的相空间. 三尺度三维奇异摄动系统的一般形式如下,
(5)
这里x,y,z∈R为3个(尺度分离的)状态变量,0<ε,δ≪1是系统的2个摄动参数,λ∈Rl为分支参数.
双摄动参数ε,δ的存在,一方面,它们带来了更多的不同层级的尺度分离,一定程度上方便了问题的处理;但另一方面,ε,δ的相对量级,将直接影响到系统(5)的分支动力学.例如:先固定δ,视ε为扰动参数,此时可认为ε=o(δ),从而系统(5)可以看作是含1个快变量和2个慢变量的奇异摄动系统;若固定ε,而视δ为扰动参数,即δ=o(ε),此时系统(5)可以看作是含有2个快变量1个慢变量的奇异摄动系统.对于含1个快变量和2个慢变量的奇异摄动系统,其局部小振幅振荡(SAOs)可由折曲线上的折结点引起,此时的折曲线和折结点的强稳定方向会形成一个奇异漏斗,折结点附近的最大鸭解会围绕弱鸭解振动;对于含2个快变量和1个慢变量的奇异摄动系统,其局部小振幅振荡(SAOs)可经时延Hopf分支产生.因此,对于三尺度奇异摄动系统(5),当ε,δ同时趋于零时,上述两种极限动力学将叠加,从而引起更为退化的问题,是一种更为困难的情形.更多关于三尺度奇异摄动系统MMOs的工作,可见文[33-39].
本文主要介绍奇异摄动系统的周期振荡及其分支问题.论文结构安排如下:第二节主要介绍三尺度奇异摄动系统(5)产生小振幅振荡和MMOs的分支机制;第三节以一个具体的食物链三尺度奇异摄动模型为例,分析引起小振幅振荡的原因.
1 三尺度三维奇异摄动系统的周期振荡
1.1 MMOs的折结点机制
先固定δ,并视ε为摄动参数,即ε=o(δ),此时系统(5)可看作是含1个快变量和2个慢变量的三维奇异摄动系统.作时间尺度变换τ=εt,得到慢系统
(6)

(7)
和退化系统
(8)
其中,二维的临界流形为
M={ (x,y,z)∈R3:f(x,y,z)=0 }.
假设临界流形M上具有如下非退化的折曲线,
Mf={ (x,y,z)∈R3:fx(x,y,z)=0,fxx(x,y,z)≠ 0 },
那么,折曲线将临界流形分为法向吸引和法向排斥两部分,分别记为
Ma=M∩{ (x,y,z)∈R3:fx(x,y,z)<0 },
Mr=M∩{ (x,y,z)∈R3:fx(x,y,z)>0 }.
退化系统(8)为微分代数系统,其限制在临界流形M上的动力学方程为
(9)
显然,系统(9)在折曲线Mf处具有奇性.将其正则化,可得正则系统
(10)
根据文[35],正则系统(10)有两类奇点:一类称为普通奇点Eo,一类称为折奇点Ef,分别定义为
Eo={(x,y,z)∈M:fyg+δfzh=0,h=0}
和
Ef={(x,y,z)∈M:fyg+δfzh=0,fx=0}.
显然,普通奇点既是正则系统(10)的奇点,也是奇性系统(9)和整个系统(6)的奇点(需要假设fy≠0);而折奇点是正则系统(10)的奇点,但不一定是奇性系统(9)和整个系统(6)的奇点.
假设p∈Ef,记λ1和λ2是系统(10)的雅可比矩阵在点p的特征值,则
(1)若λ1,λ2是实数,λ1λ2>0,则p是系统(10)的折结点;
(2)若λ1,λ2是实数,λ1λ2<0,则p是系统(10)的折鞍点;
(3)若λ1,λ2是复数,则p是系统(10)的折焦点.
若p∈Ef是系统(10)的折结点,那么系统(5)的轨线经过折结点附近会产生小振幅振荡(SAOs),其原理是因为折曲线和折结点的强稳定方向会形成一个奇异漏斗,进入奇异漏斗的强鸭解会围绕弱鸭解产生旋转,从而产生SAOs,如图1.

图1 由折结点导致的局部小振幅振荡示意图Fig.1 Schematic of local small amplitude oscillation generated by folded node

QCHD={q|(x,y,z)∈R3:fx=0,f= 0,g=0},
不难发现
|p-q|=O(δ).
1.2 MMOs的时延Hopf分支机制

(11)

(12)
和退化系统
(13)
其一维的临界流形为
S={ (x,y,z):f(x,y,z)=0,g(x,y,z)=0}.
实际上,上述定义之S,恰好为M上的一条曲线,称之为超慢临界曲线.
层系统(12)可视为单参数平面系统(z为参数),即
(14)
超慢流形S上的所有点,均为系统(14)/(12)的平衡点.若ε充分小,那么超慢流形S上满足
H={h|(x,y,z)∈S:fx+εgy=0,ε(fxgy-fygx)>0}
的点,称为时延Hopf分支的点,记为DHB. DHB点把一维的超慢流形S分成吸引和排斥部分,分别记为Sa和Sr.
在DHB点处,由于在系统(14)的线性化矩阵的特征值是一对纯虚根,轨线围绕着慢流旋转,从而产生SAOs,如图2.因此,时延Hopf分支是具有2快变量和1慢变量的奇异摄动系统产生SAOs的一种机制;它与具有1个快变量和2个慢变量的奇异摄动系统产生SAOs的奇异Hopf分支不同,时延Hopf分支与整个系统的平衡点无关,而奇异Hopf 分支是由落在折曲线上的系统的平衡点产生的,与整个系统的平衡点有关.

图2 由时延Hopf分支导致的局部小振幅振荡示意图Fig.2 Schematic of local small amplitude oscillation generated by delayed Hopf bifurcation
关于时延Hopf分支的延迟的大小,可用entry-exit函数来刻画. 假设(x0,y0,z0)∈Sa,λ=λ(z)是系统(12)/(14) 雅可比矩阵在点(x0,y0,z0) 处的特征值,φ(z0)是时延Hopf分支逃离时的z坐标,由如下entry-exit函数来控制:

这里,Reλ(z)表示λ(z)的实部.

|DHB-QCHD|=O(ε).
1.3 当0<δ=O(ε)≪1时引起小振幅振荡的CDH机制

图3 系统(5)的局部小振幅振荡示意图Fig.3 Schematic of local small amplitude oscillation of system (5)
2 一类三尺度食物链模型的周期振荡
考虑如下三尺度食物链模型
(15)
其中x,y和z分别表示食饵、捕食者和顶级捕食者的种群密度,x和y之间的捕食与被捕食关系为Lotka-Volterra型,y和z之间的捕食与被捕食关系是Leslie-Gower型的相互作用,r2z2表示顶级捕食者的交配频率与种群z的雄性和雌性的数量成正比,m<0表示弱Allee效应,0<ε,δ≪1为双摄动参数.
系统(15)是一类具有3个时间尺度的食物链模型(三维奇异摄动系统),其中相对地说,x是快变量,y是慢变量,z是超慢变量.
(1)若固定δ,视ε为摄动参数,即当ε=o(δ)时,系统(15)的临界流形是二维的,即
M={(x,y,z)∈R3|x=0}∪{(x,y,z)∈R3|y=
其中,M1为平面,M2为曲面,其上的一维折曲线为
M1和M2上分别有直线
S1={(y,z)∈R2|y=0},
以及直线和曲线
S2={(x,z)∈R2|x=K}∪{(x,z)∈R2|z=
实际上,S1和S2即为超慢临界曲线.
系统(15)位于折曲线Fc上的折奇点为

经过计算,系统(15)的正平衡点x坐标为
(2) 若固定ε,视δ为摄动参数,即当δ=o(ε)时,层系统为
(16)
系统(16)可视为单参数平面系统(z为参数),即
(17)
其超慢临界曲线为
沿着S22,系统(17)的雅可比矩阵为
于是可得
显然,当
有TrJ=0.而
detJ=εxy(O(ε)+a1b1)>0.
因此,发现系统(15)混合模式振荡(MMOs)中的小振幅振荡是由时延Hopf分支引起,如图4所示.图4a和b分别显示系统(17)有1个和2个正平衡点的情形.正平衡点的个数和位置,如图4所示,将对系统的动力学产生很大的影响.具体的详细分类和过程,略.
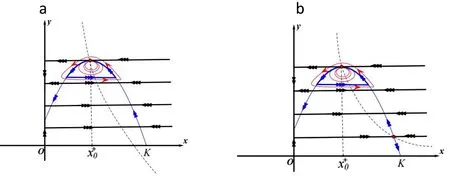
图4 系统15由时延Hopf 分支引起的局部小振幅振荡示意图Fig.4 Local small amplitude oscillation of system 15 generated by delayed Hopf bifurcation
