基于ARIMA模型和K-means聚类分析的动态规划算法
2022-07-14徐建闽首艳芳
徐建闽,臧 鹏,首艳芳
(1. 华南理工大学 土木与交通学院,广东 广州 510640; 2. 华南理工大学 广州现代产业技术研究院, 广东 广州 510640)
0 引 言
寻找最短路径是智能交通系统最重要的功能之一。无论是否处在疫情环境中,环境是否剧烈变化,实时自动化的信息采集方式均能保证信息采集的准确性、安全性和清洁性[1-2],所以研究基于浮动车数据的最短路径算法具有深远的意义。
近年来,寻找最短路径的主要方法通常分为两类,即受干扰的最短路径寻找和不受干扰的最短路径寻找,采用的方法有:权重图匹配法[3]、自适应路径寻找[4-6]和马尔科夫决策模型[7]。而基于浮动车数据的算法多选择权重图匹配法。权重图匹配法是根据多种参数,如道路距离、等级等设置权重,以求排除不可能的候选路段,从而降低了地图匹配算法的计算复杂度。然而,权重的确定具有很强的主观性,同时计算出来的最短路径不一定是最优解,所以研究排除干扰、耗时短且获得最优解的算法是现今研究的趋势。
建立基于ARIMA模型和K-means聚类分析的动态规划算法,并利用滴滴出行数据在成都市的二环区域内进行了测试,最后通过实验结果表明,新的算法以较低的计算量提供了高质量的时间解。
1 理论方法
1.1 ARIMA模型
时间序列模型可以通过把时间序列数据按照曲线拟合和参数估计的方法来建立数学模型的一种理论和方法,是参数化模型处理动态随机数据的一种实用方法,可以预测未来。差分整合移动平均自回归(ARIMA)模型经常运用在交通环境中且预测效果良好[8-9]。ARIMA模型由3部分组成。
1.1.1 自回归过程
Xt=α1Xt-1+α2Xt-2+…+αiXt-i+…+αpXt-p+βt
(1)
式中:αi为预测模型参数;Xt-i(i=1,…,p)为前p期数据;βt为随机扰动项。
由于ARIMA模型预测轨迹旅行时间的精度受到数据缺失的影响较大,且信号灯对交叉口上、下游道路的作用高于交叉口上游或下游道路的作用,所以采用路段中点取样法,即采样点为路段中点,预测路段的旅行时间并与实际的旅行时间对比后将其组合来预测轨迹旅行时间。组合的方法能够填补缺失数据,同时减少信号灯及突发事故的影响,使预测效果有所改善。
第i期轨迹旅行时间的计算公式为:
(2)
式中:xt-i,mn,lk为同期组合轨迹的路段旅行时间;n、m分别为路段起点的经度、纬度;l、k分别为路段终点的经度、纬度;x′t-i,mn,lk为同期路段旅行时间的预测值为式(3):
(3)
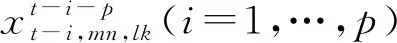
为进一步减小采样时出现的区域性截断和载体过少导致数据缺失等问题,采用如下处理规则:第i期的旅行时间xt-i通过前一段时间内的旅行时间样本数据进行计算,若数据充足,则采用所有数据取平均值的方法;若数据缺失,则用已知的前期数据做线性推导。计算公式为:
(4)
式中:Si,p为第i期的轨迹旅行时间的采样数据,共有A个;Si′和Si″为i期前i′时刻和i″时刻的2个能采集到的旅行时间数据,数据充足的标准为Q个。
1.1.2 差分过程
差分过程处理非线性、非平稳的序列数据,并将非线性、非平稳的序列数据转化为平稳的数据。式(5)为一阶差分变形,能够转化为ARMA模型。同时,差分过程可以提高预测精度。
ΔXt=Xt-Xt-1
(5)
1.1.3 移动平均过程
移动平均过程是研究随机扰动项的序列相关性。式(6)是q阶的移动平均过程:
βt=δt-θ1δt-1-θ2δt-2-…-θqδt-q
(6)
ARIMA模型可以较为精准的预测轨迹的旅行时间,但是无法找到区域内最短路径,所以建立基于ARIMA模型的动态规划模型来实现目标。
1.2 基于ARIMA模型的动态规划模型
建立基于ARIMA模型的动态规划模型,目标函数为:
(7)
但是,随着道路网规模的扩大,访问状态会增加,动态规划函数往往面临维数灾难和运算过慢的问题,所以简化为:
(8)
式中:x′mn, lk为每段路段的ARIMA模型的预测值,其公式为:
(9)
1.3 基于ARIMA模型和K-means聚类分析的动态规划算法
动态规划算法的挑战之一是在为特定的状态做出决策时,确保探索和利用策略之间的平衡。只使用探索策略可能会导致选择似乎最优值的决策而陷入局部最优。另一方面,仅采取利用策略可能会导致随机访问每个状态,这会大大增加计算时间和较差的估计值。
在文献中,一些技术,如状态约简技术[10]和随机前瞻算法[11-12]被用来解决以上问题。K-means 聚类分析[13]的起源是信号处理的一种向量量化方法,目的是把r个点划分到s个聚类中,使得每个点都属于离它最近的均值(即聚类中心)对应的聚类中,以此作为聚类的标准。为集群耗时相似的路径,从而避开耗时长的区域选择耗时较短的路径,减少查询状态的范围,提高运算速度。将K-means的特征值作为路段的预测平均速度。
同时,为保证预测精度,建立基于ARIMA模型和K-means聚类分析的动态规划算法(DPBAK),具体步骤为:
步骤1输入每段路的每期实际的旅行时间xt-i,mn, lk,路段的长度Smn, lk,聚类个数s。
步骤2用ARIMA模型预测xmn, lk。
步骤3K-means聚类分析将各个路段的按特征值分为s类,并从DLng和DLat集合中剔除不符合要求的路段集合。
步骤4用Dijkstra算法求解最短路径。
步骤5输出T。
这种基于浮动车数据的组合算法的优点在于:①采样时间短,可以减小每一阶段的期望计算;②可以随时计算未来的最短旅行时间,且越接近目的地越可靠;③快速计算不同位置的最优值;④不会受外界干扰而引起大的波动。
1.4 对比算法
对于无法获得最优解的大型实例,笔者使用H.SHUAI等[12]提出的分段线性函数改进的近似动态规划(ADPED)进行基准测试,其得到的近似最优解非常接近全局最优解。
2 实验及实验结果
2.1 数据来源
笔者的研究数据来源于滴滴出行“盖亚”数据开放计划(网址:https:∥gaia.didichuxing.com)的2016年10月成都市二环区域65 km2的快专车平台的订单司机轨迹数据。选择2016年10月28日的数据,轨迹点的采集间隔是2~4 s,起点和终点分别是双桥社区西南1门和蓝谷公寓西南门(S-L),如图1。为简化运算,将区域中的单行道等特殊车道剔除。
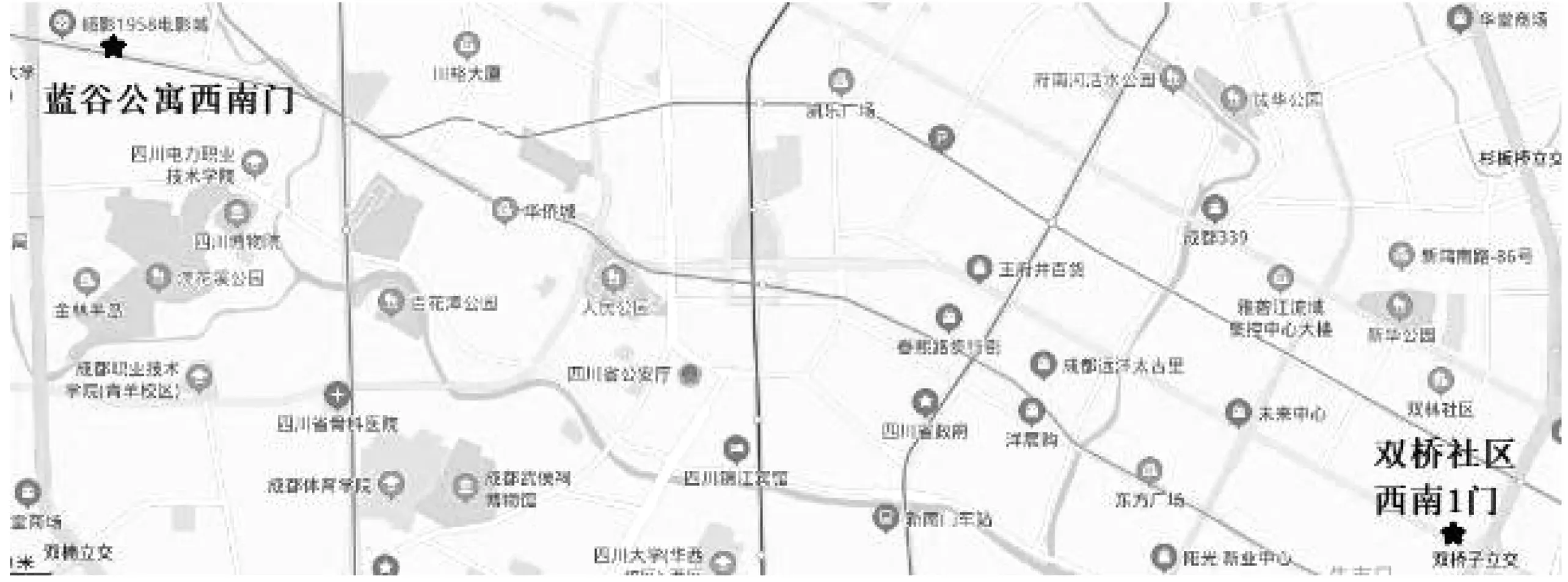
图1 双桥社区西南1门和蓝谷公寓西南门地图
2.2 运算环境
笔者提出的算法用python语言实现,所有的实验均在个人电脑上进行,具体配置为Intel Core i5 2.2 GHz处理器和4.00 GB内存。
2.3 评价指标
为评价算法的预测性能,选择绝对百分误差(MAPE)计算预测值与实际值的偏差,其计算公式为:
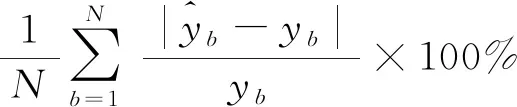
(10)
2.4 实验结果
根据交通拥堵指数的5个级别,令k=5。算法从DLng和DLat集合中逐步剔除旅行时间由高到低的集合,如图2,DPBAK-1是DPBAK算法剔除的速率集合[0,25.6],DPBAK-2是DPBAK算法剔除的速率集合[0,38.12],以此类推。实验结果如图3~图6,如表1。
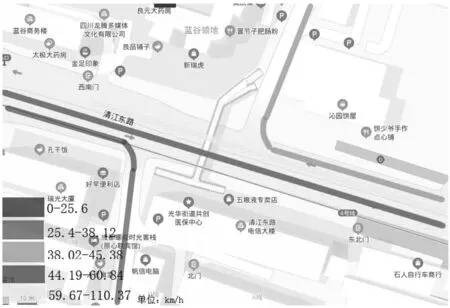
图2 DPBAK算法在21:15部分聚类集合
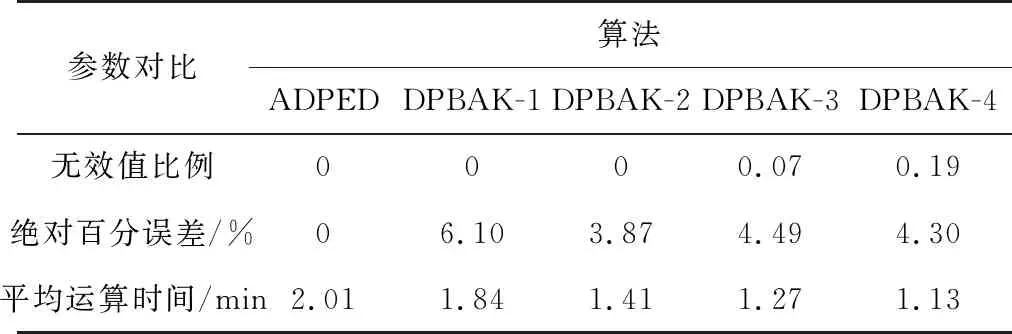
表1 DPBAK与ADPED 对比
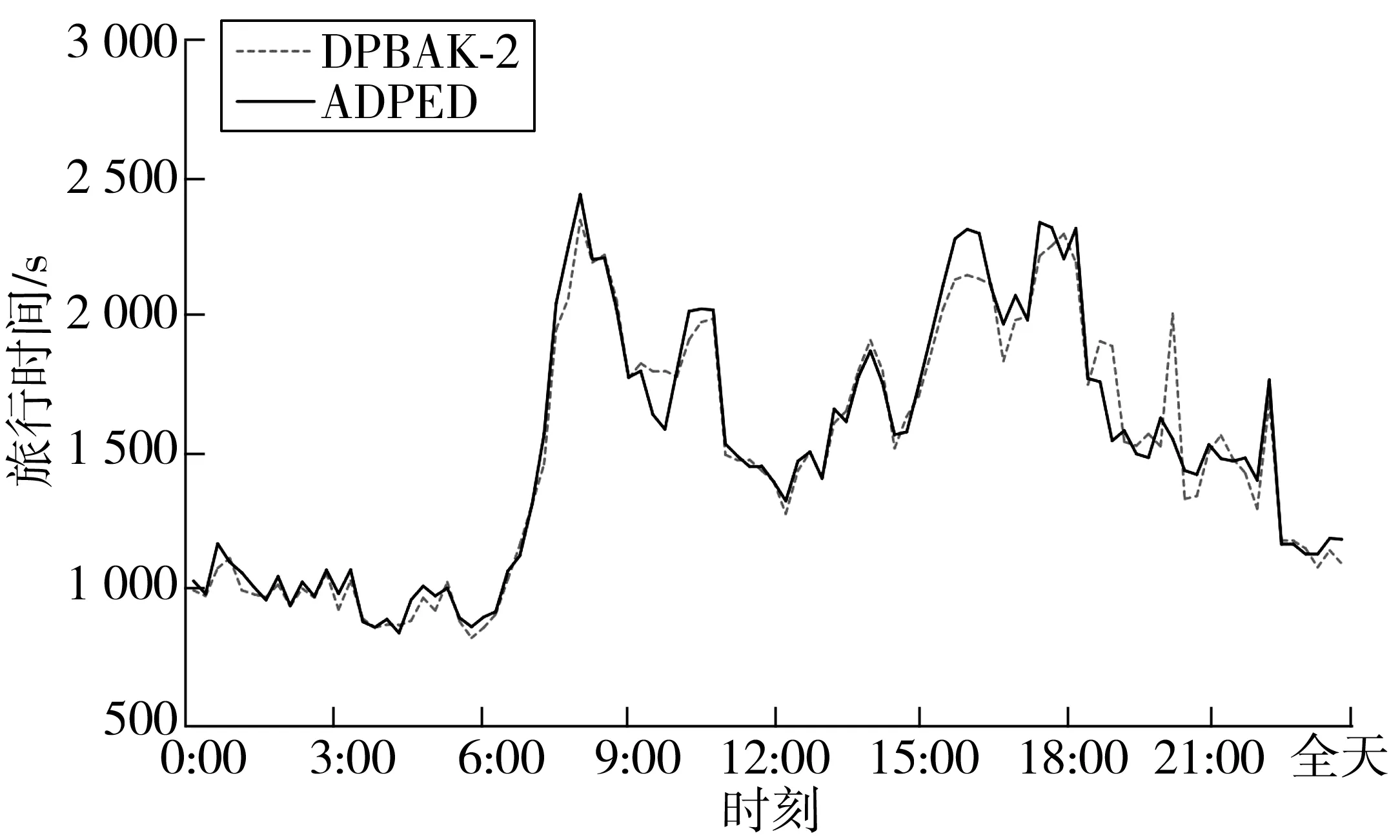
图3 DPBAK- 1与ADPED对比
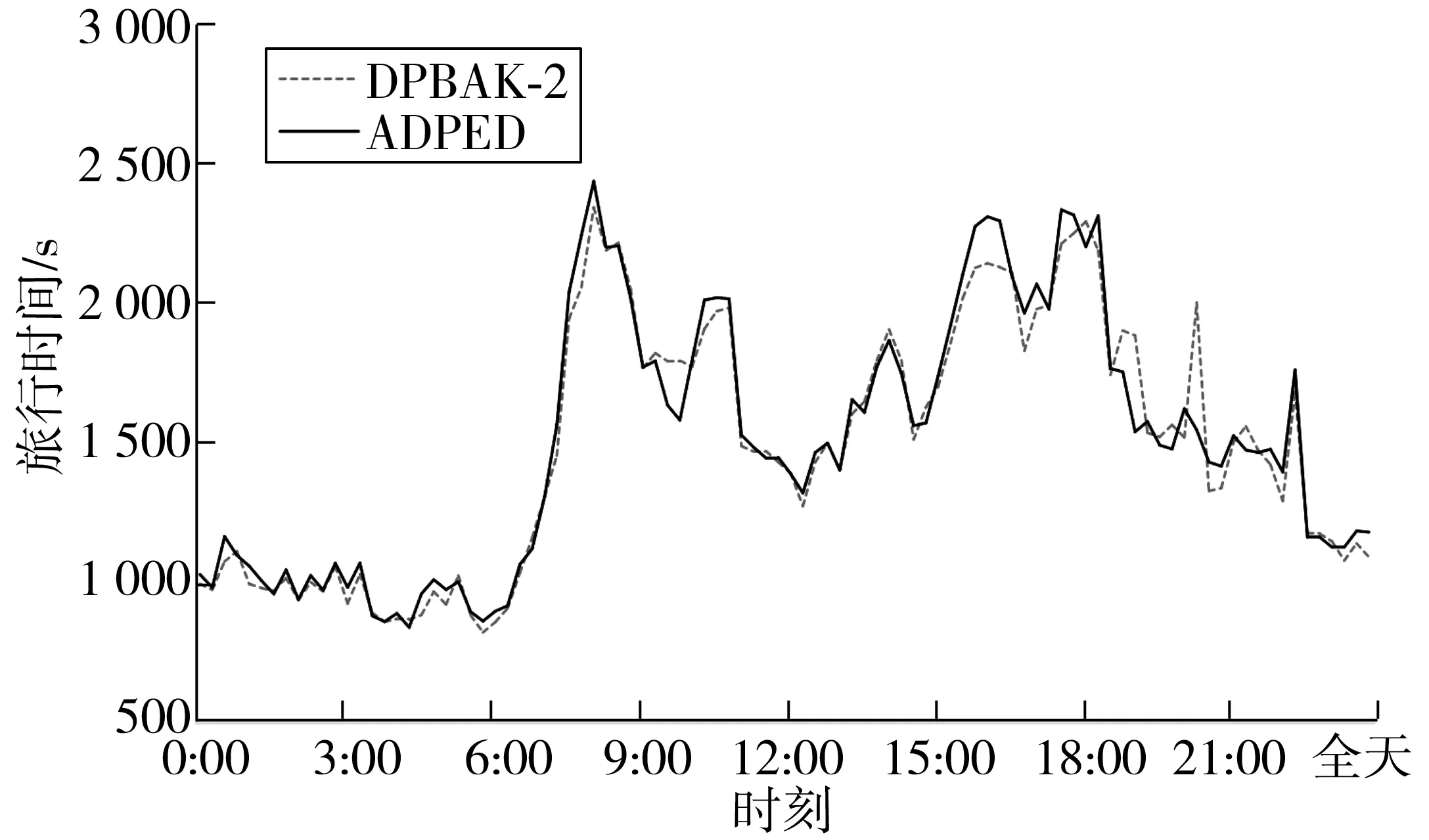
图4 DPBAK-2与ADPED对比
实验结果表明:算法较快运算出贴近最优解的结果。与ADPED 相比,算法运算时间均低于2.010 min,平均百分误差低于6.5%,无效值比率小于20%。这说明剔除拥堵或者说是速度较慢的路段集合,在一定范围内可以提高运算效率和准确率。随着对于集合剔除数量的增加,运算时间明显降低,平均误差值明显减小。但是值得注意的是,运算时间的变化率和平均误差在剔除最大的2个集合后不会明显增加,平均误差甚至会略有增加,表1中DPBAK-3、DPBAK-2、DPBAK-4的平均误差分别为4.49%、3.87%和4.3%,运算时间分别为1.271 min(-36.8%)、1.413 min(-29.7%)和1.130 min(-43.8%)。这说明剔除过多的集合会减少查询状态,提高运算速度,但是剔除过多会导致两种情况:绕路严重,增加旅行时间;或是无法得到可行解。从图3~图6及表1来看,算法与近似最优解波动较为贴合。这证明了算法有效性。同时,剔除较多的集合后,无效值和MAPE异常值明显出现在日间。这可能与日间的车速波动较大有关。随着剔除的集合增加,无效值比例和MAPE异常值数量明显增加。这也佐证了“剔除过多的集合会减少查询状态,提高运算速度,但是剔除过多会导致绕路严重增加旅行时间”的论点。
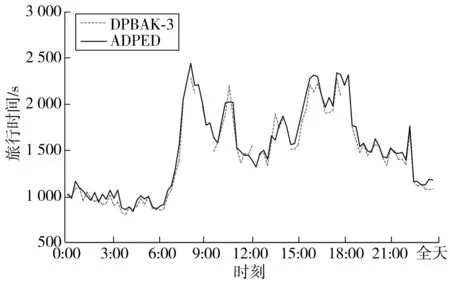
图5 DPBAK-3与ADPED对比
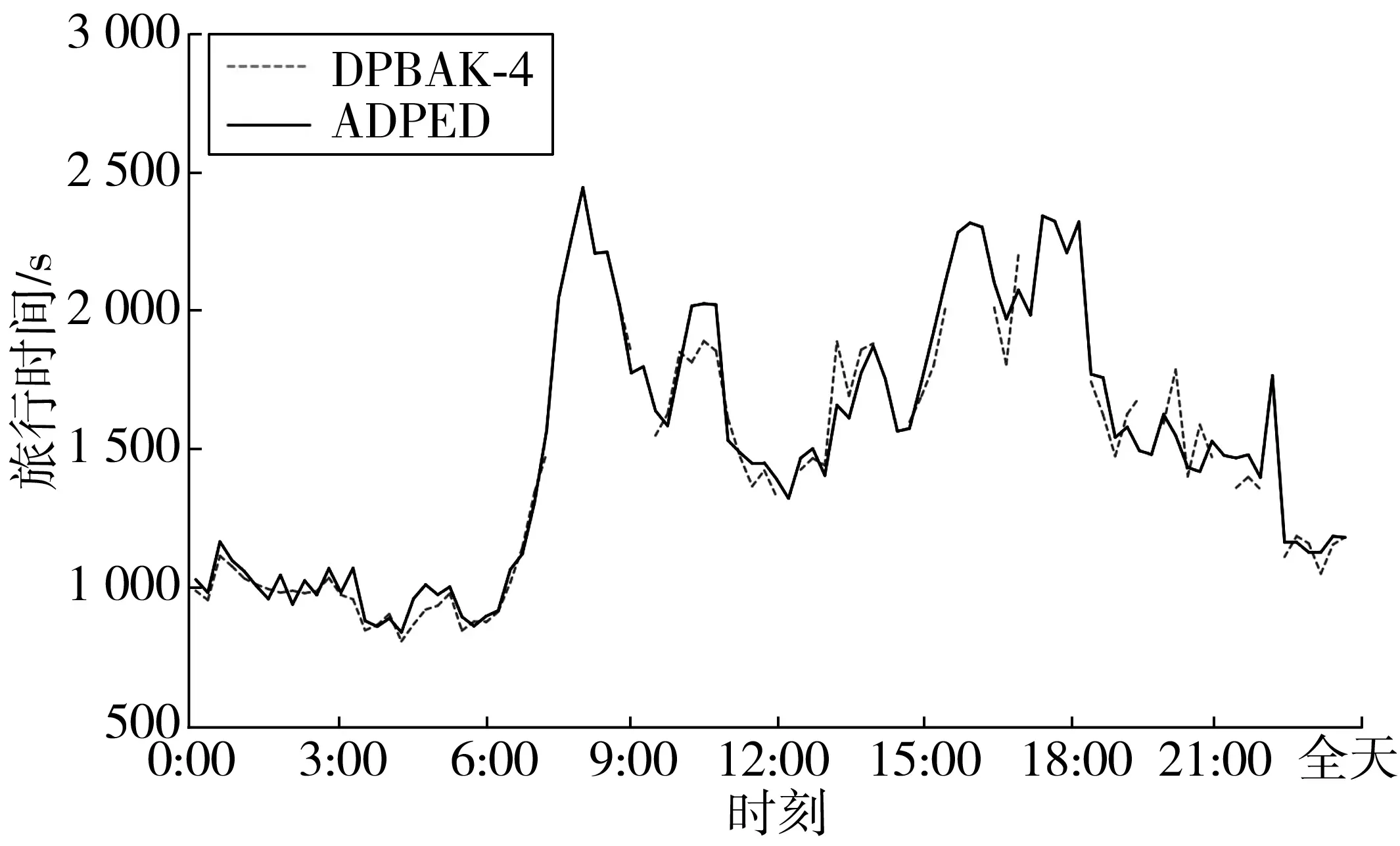
图6 DPBAK-4-与ADPED对比
3 结 论
建立了基于ARIMA和K-means聚类分析的动态规划算法来预测最短路径,并通过实验得到以下结论:
1)提出了新的最短路径算法且算法能较快运算出贴近最优解的解。
2)剔除拥堵或速度较慢的路段集合,在一定范围内可以提高算法的运算效率(+8.2%到+43.8%)和降低误差(3.81%到6.10%)。
3)剔除过多的集合会使算法性能提升,但剔除过多会导致得不到最优解,甚至是得不到解的情况发生。
4)与ADPED 相比,算法运算时间均低于2.010 min,平均绝对百分误差低于6.5%,无效值比率小于20%。
