虚拟荷载法在钢-混凝土组合梁计算中的应用
2022-07-14李雪峰陆元春
李雪峰,陆元春,周 良
(上海市城市建设设计研究总院(集团)有限公司,上海 200125)
0 引 言
钢-混凝土组合梁能充分发挥钢材和混凝土各自材料的特性,被大量应用于桥梁结构中[1-2]。不过,由于所用材料的特性不同,钢-混凝土组合梁的受力变得更加复杂。与混凝土梁相比,钢-混凝土组合梁在的收缩、徐变、材料温差等作用下均产生截面次应力[3-4]。若将混凝土收缩、徐变及材料温差对梁产生的附加作用等效为作用于截面内随时间变化的预加力,并将混凝土及钢梁视作变形协调的脱离体,则可便捷求解截面内因收缩、徐变、材料温差等作用产生的次应力。利用有限元软件对组合梁进行分析,可获得组合梁在各种作用下的结构应力[5],再用解析法进行补充[6-7]。
我国1989年颁布的TBJ 24—89《铁路结合梁设计规定》给出了简支梁温差应力的计算式;最后规定收缩引起的截面应力可等效为温度降低引起的应力,因而可采用温差应力式计算。然而,郑纬奇等[8]研究发现TBJ 24—89《铁路结合梁设计规定》给出的收缩应力计算偏于不足。
笔者依托国家标准GB 50917—2013《钢-混凝土组合桥梁设计规范》的编制工作,推导了基于虚拟荷载法的简支组合梁截面温差应力增量计算式;结合考虑徐变影响的有效弹性模量法,推导了基于虚拟荷载法的简支组合梁截面收缩应力增量计算式;并以某一45 m跨径工字钢-混凝土组合梁为例,分别采用虚拟荷载法、ANSYS有限元法及TBJ 24—89《铁路结合梁设计规定》推荐的计算式计算了组合梁的温差应力及收缩应力,并进行了对比分析。研究结果验证了虚拟荷载法应力计算式的准确性。
1 虚拟荷载法介绍
虚拟荷载法的基本指导思想是:将钢梁和混凝土梁之间由于收缩、徐变及材料温差等作用产生的相对变形按规则等效为虚拟荷载,则组合梁在收缩、徐变及材料温差作用下的应力增量与施加对应虚拟荷载后的应力增量相等。
由于钢-混凝土组合梁包含2种特性不同的材料,为了方便计算,根据等效换算原理,即保持换算前后单元面积承受的合力相等且应变相等,按照式(1)、式(2)将混凝土等效换算为钢材:
(1)
(2)
式中:n0为钢材与混凝土的弹性模量之比;Es为钢材的弹性模量;Ec为混凝土的弹性模量;A0为换算截面面积;Ac、As分别为混凝土桥面板截面、钢梁截面面积。
2 温差应力
2.1 虚拟荷载法计算式
假定钢梁与混凝土梁之间存在温差ΔT℃,且混凝土的温度低于钢梁的,混凝土线膨胀系数为αT。采用虚拟荷载法求解钢-混凝土组合梁温差应力过程如图1。

图1 虚拟荷载法求解钢-混凝土组合梁温差应力计算过程示意
1)假定钢梁与混凝土桥面板之间无连接,混凝土桥面板在温差作用下自由变形,则两者之间的温度伸长量之差ΔL=LαTΔT,相应的应变量εT=-αTΔT。此时,钢梁中应力和应变均为0。
2)实际工程中,在钢梁与混凝土桥面板之间设有抗剪连接件,它可阻止两者发生相对滑移。为了补偿由于温差产生的相对滑移应变,需在混凝土桥面板形心轴位置施加一个虚拟荷载P,使混凝土桥面板均匀受拉,拉应变ε=αTΔT。此时,混凝土桥面板和钢梁的变形一致,虚拟荷载P=-AcEcαTΔT,组合梁内混凝土桥面板应力σT,c1、钢梁应力σT,s1分别如式(3)、式(4):
σT,c1=-EcαTΔT
(3)
σT,s1= 0
(4)
3)恢复钢梁与混凝土桥面板间的连接,此时钢梁与混凝土桥面板的应变相同,因此,恢复连接并不会使组合梁中应力发生变化。
4)为了抵消施加的虚拟荷载P,需要在混凝土桥面板形心轴位置反向施加P0=AcEcαTΔT,因而,组合梁截面处于偏心受压状态。此时,组合梁内混凝土桥面板应力σT,c2、钢梁应力σT,s2分别如式(5)、式(6):
(5)
(6)
式中:y0为混凝土桥面板形心至换算截面形心的距离;yc、ys分别为混凝土桥面板、钢梁上某点至换算截面形心的距离;I0为换算截面惯性矩。
5)将以上各步的应力、应变进行叠加即为最终状态。此时,组合梁的外力合力为0,符合变形协调条件和内力平衡条件。最终,组合梁内混凝土桥面板、钢梁温差应力σT,c、σT,s分别如式(7)、式(8):
σT,c=σT,c1+σT,c2=
(7)
(8)
2.2 TBJ 24—89《铁路结合梁设计规定》计算式
根据TBJ 24—89《铁路结合梁设计规定》,钢-混凝土组合梁由于材料温差引起的混凝土桥面板应力σT,c、钢梁应力σT,s分别按照式(9)、式(10)计算:
(9)
(10)
式中:d为混凝土桥面板的截面重心至钢梁截面重心间的距离;n为计算温度变化影响时钢与混凝土的弹性模量比;Ic、Is分别为混凝土板与钢梁截面惯性矩。
3 收缩应力
3.1 虚拟荷载法计算式
在计算组合梁由于混凝土收缩效应产生的应力时,应考虑徐变的影响。参考欧洲规范Eurocode4:DesignofCompositeSteelandConcreteStructures[9],GB 50917—2013《钢-混凝土组合桥梁设计规范》给出了考虑徐变对组合梁影响的有效弹性模量Ecsφ,即调整后的混凝土弹性模量,按式(11)计算:
(11)
式中:ψL为根据荷载类型确定的徐变因子,永久作用时ψL=1.1,混凝土收缩作用时ψL=0.55,用于调整内力的强迫位移作用时ψL=1.5;φ(t,t0)为加载龄期t0、计算龄期t的混凝土徐变系数;其他符号同前。
采用虚拟荷载法计算组合梁收缩应力时,需先将收缩变形换算为作用于混凝土桥面板形心的虚拟荷载。因此,考虑徐变效应的混凝土桥面板收缩变形等效虚拟荷载按式(12)计算:
P0=EcsφAcεsh(t,τ)
(12)
εsh(t,τ)=εsh,c0β(t,τ)
(13)
式中:εsh(t,τ)、β(t,τ)分别为混凝土桥面板与钢梁结合龄期为τ、计算龄期为t的混凝土收缩应变值、收缩折减系数;εsh,c0为混凝土名义收缩系数。
考虑徐变效应的混凝土桥面板应力σsh,c、钢梁应力σsh,s分别按式(14)、式(15)计算:
(14)
(15)
式中:n0,L、A0,L、I0,L分别为考虑混凝土有效弹性模量的钢材与混凝土的换算弹性模量之比、换算截面面积、换算截面惯性矩。
3.2 TBJ 24—89《铁路结合梁设计规定》计算式
现行TBJ 24—89《铁路结合梁设计规定》的组合梁收缩应力计算式是基于混凝土板与钢梁曲率协调与结合面变形协调的弹性力学理论得出的,详见相应条文,在此不予赘述。
4 验证分析
参考工程实际中常用的组合梁截面形式,笔者以一个45 m跨径工字简支钢-混凝土组合梁为例来验证虚拟荷载法的有效性,桥梁截面形式如图2[10]。混凝土桥面板采用C40混凝土,钢梁采用16Mn钢。采用虚拟荷载法、TBJ 24—89《铁路结合梁设计规定》推荐方法进行应力计算,再用ANSYS有限元软件模拟该结构在温差、收缩作用下的截面应力,并对3种方法计算的结果进行了对比分析。
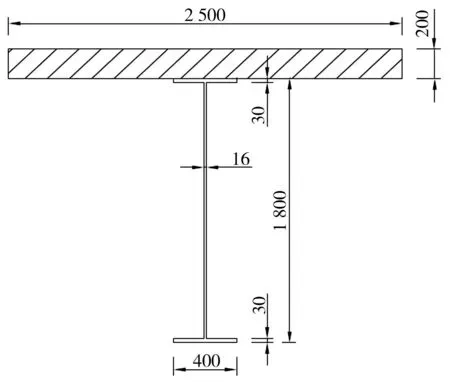
图2 钢-混凝土组合梁截面
4.1 温差应力
当混凝土桥面板与钢梁温差ΔT=15 ℃(混凝土桥面板温度低于钢梁温度)时,分别采用虚拟荷载法〔式(7)~式(8)〕、ANSYS有限元法、TBJ 24—89《铁路结合梁设计规定》〔式(9)~式(10)〕计算组合梁的温差应力σT;统计了TBJ 24—89《铁路结合梁设计规定》及虚拟荷载法计算结果与有ANSYS限元法计算结果的相对误差绝对值|δ|,见表1。

表1 钢-混凝土组合梁温差应力及相对误差的计算结果
从表1可以看出:虚拟荷载法、TBJ 24—89《铁路结合梁设计规定》计算的组合梁截面温差应力相对误差绝对值最大分别为1.605%、3.081%,比较而言,虚拟荷载法计算的组合梁截面温差应力值更准确。
4.2 收缩应力
4.2.1 收缩应变计算
1)虚拟荷载法计算
假定桥面板与钢梁结合时刻混凝土的龄期为7 天,桥梁所处环境的年平均相对湿度为40%~70%[11]。算例中各参数根据GB 50917—2013《钢-混凝土组合桥梁设计规范》取值:εsh,c0=0.529×10-3,β(t,τ) = 0.95,φ(t,t0) = 2.99,ψL=0.55,Ec=3.25×104MPa,Es=20.5×104MPa,Ac=2 500×200=500 000 mm2,计算得:
εsh(t,τ)=εsh,c0×β(t,τ)=0.529×10-3×0.95=
0.503×10-3
P0=EcsφAcεsh(t,τ)=1.23×104×2 500×200×0.503×10-3=3 093 450(N)
2)TBJ 24—89《铁路结合梁设计规定》计算
TBJ 24—89《铁路结合梁设计规定》将由于混凝土收缩引起的截面内力等效为由混凝土板均匀降温15 ℃引起的截面内力,此时混凝土收缩应变εsh,c=15×1×10-5=0.150×10-3。
4.2.2 收缩应力计算
表2为分别采用虚拟荷载法与TBJ 24—89《铁路结合梁设计规定》计算的钢-混凝土组合梁的收缩应力σsh值。

表2 钢-混凝土组合梁收缩应力计算结果
从表2中可以看出:
1)2种方法计算的简支组合梁截面各验算部位的收缩应力相差较大,虚拟荷载法计算的大约是TBJ 24—89《铁路结合梁设计规定》计算的3倍。
2)虚拟荷载法采用的弹性模量比n1=16.762,与TBJ 24—89《铁路结合梁设计规定》的取值15相差不大,表明混凝土弹性模量取值不是导致收缩应力相差较大的原因。
3)虚拟荷载法计算的混凝土收缩应变为0.503×10-3,而TBJ 24—89《铁路结合梁设计规定》等效的混凝土收缩应变为0.150×10-3。可见,造成收缩应力差别较大的原因是TBJ 24—89《铁路结合梁设计规定》对收缩应变估计不足。
4)TBJ 24—89《铁路结合梁设计规定》采用折减混凝土弹性模量的方法考虑了徐变对钢-混凝土组合梁受力的影响,但其仅仅根据混凝土强度等级给出了不同的弹性模量比取值,未考虑混凝土龄期对徐变的影响;《铁路结合梁设计规定》将收缩应变的计算等效为混凝土的温度变化,根据混凝土的灌注方式不同取不同的等效温度,未考虑混凝土与钢梁结合龄期对收缩的影响;《铁路结合梁设计规定》未根据年平均相对湿度来选取收缩值,最终导致混凝土收缩应变取值不足。
5 结 论
推导了用虚拟荷载法计算钢-混凝土组合梁在收缩、徐变及材料温差作用下截面应力增量的计算公式;选择了一个45 m跨径工字钢-混凝土组合梁进行验算,对比分析了虚拟荷载法、TBJ 24—89《铁路结合梁设计规定》、ANSYS有限元法3种方法的计算结果。研究得到以下主要结论:
1)虚拟荷载法可以用于计算钢-混凝土组合梁中由混凝土徐变、收缩,及材料温差等引起的截面应力增量,计算结果与有限元计算结果吻合较好。
2)与TBJ 24—89《铁路结合梁设计规定》的计算方法相比,虚拟荷载法可以考虑更多的因素,同时其求解思路还可以应用于连续梁中。
3)TBJ 24—89《铁路结合梁设计规定》对收缩应变估计不足,应引起业内的重视。
