织物透气性计算方法的探究
2022-07-14冯华峰王刚强张建立王灏洁
冯华峰,刘 晨,王刚强,张建立,王灏洁
(1.浙江理工大学科技与艺术学院 纺织服装学院,浙江 上虞 312369; 2.余姚永坚自控设备有限公司,浙江 余姚 315400; 3.浙江灏宇科技有限公司,浙江 绍兴 312300)
随着经济社会的不断发展,人们对着装的舒适性有了更高的要求。透气性是评价服装舒适性的一个重要指标,研究服装的透气性对纺织品的生产和使用具有指导意义。
神经网络研究法和公式拟合推算法常用于织物透气性的研究。神经网络研究法即通过构建合适的人工网络模型对要分析的影响因子进行层层拟合推演,其中基于PPR神经网络[1]的数学模型被认为具有很好的拟合效果,可分析和预测具有相同特性的某类织物的透气性。但该算法只可选取特定的影响因子作为输入层数据,而不同类型织物的影响因子有所差异,所以其适应范围存在局限性。公式拟合推算法适用范围则较广且简单方便。其先根据模型假设织物经纬纱在制造过程中形成的间隙为矩形,然后将矩阵式排列的矩形按照平行管束来模拟,运用流体力学理论中的哈根-泊肃叶(Hagen-Poiseuille)定律来模拟织物理论透气性[2-3],并结合织物结构参数拟合得出拟合公式,通过SPSS软件进行回归分析[4-5]。回归分析中高阶曲线的拟合模型适应性不强,一般采用线性拟合分析。
本文选取16种不同材质的织物作为样本,测试其透气率,首先把经纬交织的孔隙按照近似矩形来计算,再根据Hagen-Poiseuille定律计算其结构参数中经、纬纱线密度,经、纬纱表观直径,得到该织物的等速当量直径和流量当量直径;利用MatLab软件中的曲线拟合工具对得到的不同拟合模型进行比对分析[6],择优选取最佳的拟合方法;对不同织物的透气率数据进行拟合推演,从而计算该数学模型的残差方差和以及均方根误差,将其控制在最小值。进而实现对部分织物透气性的预测,为织物的生产和使用给出指导意见。
1 织物透气性
织物两侧存在气压差,空气通过织物的孔隙从高压侧向低压侧透过的性能即为织物透气性,常用于分析实际工程问题[7-8]。空气能够透过织物的主要原因有2个,一是通过织物中经纬纱线交织形成的孔隙,二是通过纱线内纤维结构中本身存在的孔隙,其中前者占绝大因素,因此本文只考虑纱线交织后留下的孔隙。通过Y511B型织物密度镜(温州大荣纺织仪器有限公司)可以直观地看到织物中的间隙孔都是从一边贯通到面料的另一边,当气体流经面料间隙孔时,其形状由小变大,间隙孔横截面呈现出类似喇叭形状的螺旋状态,当气体流过该形状的截面时产生涡流,形成流体上常讲的紊流运动[9]。因此该过程可近似于流体通过多孔物体,可用平行管束的理论模型来模拟分析织物的透气过程,即织物透气性用流体力学理论中的Hagen-Poiseuille定律来计算。
首先提出假设,把织物在织造过程中由于经纬纱线交织产生的间隙孔设定为矩形,其分布按矩阵式排列,且孔径大小一致,按照流体力学理论模型,间隙孔可用流体中等速当量直径dh和流量当量直径dL2种方法来表示。根据其适应性得出织物在透气过程中出现层流及紊流时可以用等速当量模型来表达,在紊流过渡区用流量当量模型来表达。
1.1 等速当量直径
根据流体力学模型,其等速当量直径[10]dh(mm)为:
(1)
式中:a、b分别为矩形风管的边长,mm。
将织物的经、纬向密度分别记作Pj、Pw( 根/(10 cm));将织物经纱和纬纱的表观直径记作dj、dw(mm),代入式(1)得到式(2):
(2)
1.2 流量当量直径
根据流体力学模型,其流量当量直径dL(mm)为:
(3)
式中:a、b分别为矩形风管的边长,mm。
同理可得:
2 织物透气性的测定
2.1 设备仪器与织物样品
设备仪器:Y511B型织物密度镜(温州大荣纺织仪器有限公司);YG141型织物厚度仪YG002型纤维分析仪(泉州市美邦仪器有限公司);KES-F8-AP1型织物透气性测试仪(加多技术有限公司)。
织物样品:选取16种比较常见的纺织品面料,为避免每次实验对织物的影响,将每种面料分成4组,第1组用于厚度测量,裁剪成30 cm×30 cm;第2组用于纱线密度的测量;第3组用于测量纱线的表观直径;第4组用于织物透气性测试。
2.2 织物参数的测量方法
织物密度:参照GB/T 4668—1995《机织物密度的测定》,用织物密度镜观察10 cm以内织物经纬纱交织中2个方向的纱线根数,计作经纱线密度Pj、纬纱线密度Pw。
织物厚度:参照GB/T 3820—1997《纺织品和纺织制品厚度的测定》,将30 cm×30 cm的试样放置于织物厚度仪的圆盘上,刻度调零后,按下开始按钮,压脚自动压下,待指针稳定后读取刻度,对每块试样的厚度分别进行10次测量,每次取不同的平整部位,最后取织物厚度平均值L(mm)。
织物纱线表观直径:采用纤维分析仪获取织物经纬交织的单元结构图片,运用软件Scope image选项中的测量工具,在同一根经线或者纬线中选取10个有效的测量位置进行直径测量,然后计算该数据的算术平均值,得到织物经、纬纱线的表观直径dj、dw(mm)[12]。
织物透气性:参照GB/T 5453—1997《纺织品 织物透气性的测试》,采用织物透气性测量仪测试,对试样织物在压降为100 Pa下进行10次有效测量,求取算术平均值。
等速当量直径dh根据式(2)计算得到,流量当量直径dL根据式(4)计算得到,织物样品各结构参数测量值见表1。
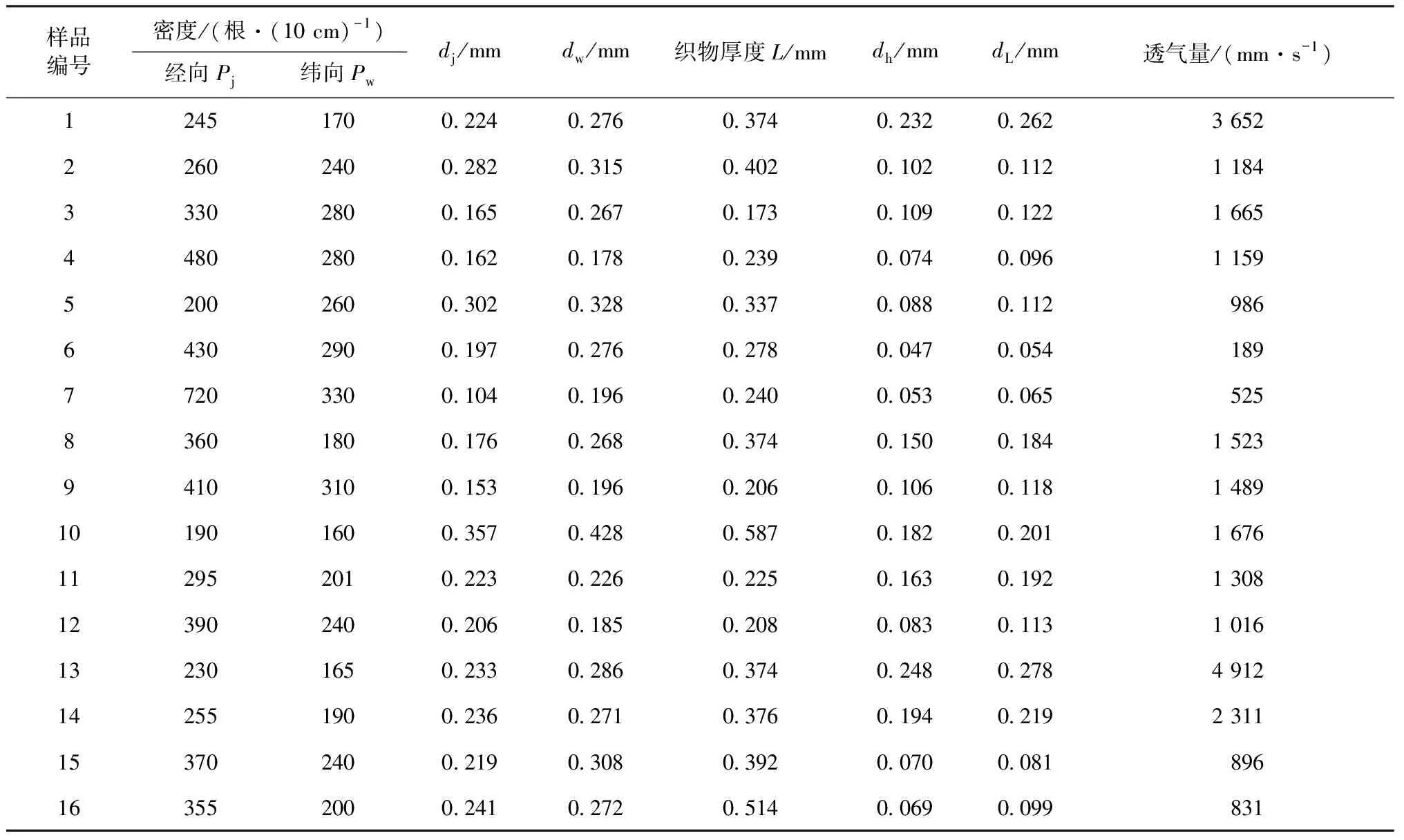
表1 织物样品各结构参数测量值Tab.1 Measured values of fabric structure parameters
3 基于MatLab的曲线拟合
3.1 拟合效果的评价及比较
曲线拟合效果常通过拟合误差与曲线形状作为拟合算法的评估参数。以此为标准,在MatLab的常用工具箱中,选取相应参数进行拟合效果的评定,所选参数如下:
SSE:输入与输出误差的平方和。此统计量可反映拟合值的偏差,越接近0值表示拟合输出与输入匹配度越高。
R-square:多重测定系数。其数值在0~1之间变化,如果数据越接近1,则表示所拟合的曲线因变量与模型中的输出值越相关。
Adjust R-square:自由度调整测定系数。越接近1表示模型匹配度越高。
RMSE:拟合数据与输入数据差分值的均方根误差。越接近0表示拟合输出与输入匹配度越高。
利用2.2所测量的等速当量直径dh与透气性2组数据,在MatLab的工具箱中分别选用7种数据拟合方法,统计数据拟合后输出的评估参数,即SSE、R-square、Adjust R-square、RMSE,结果如表2所示。
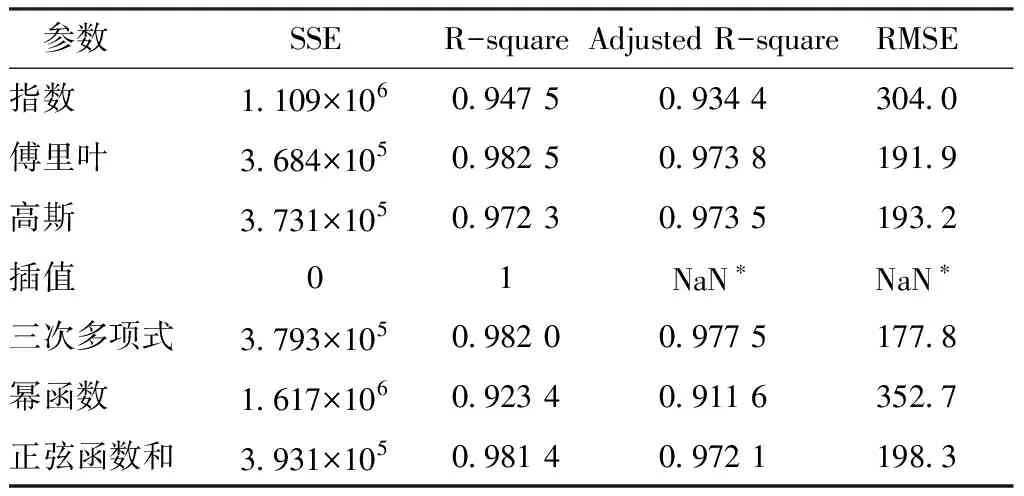
表2 各类拟合方法的评定参数比较Tab.2 Evaluation parameter ratio of various fitting methods
从表2可以看出,误差的平方和(SSE)普遍较大,选择用多重测定系数(R-square)为第一评价指标。由于插值模型出现不合理参数,因此暂定傅里叶级数拟合、三次多项式拟合和正弦函数之和拟合的3种方法最为优越,但三者评价指数比较接近,因此需要通过流量当量直径dL与实际透气率之间的拟合情况再一次比较上述3种模型的评估参数,从而确定其中最优的一种模型,使该模型能最大程度地满足2种孔隙直径的计算方法。
利用2.2节所测量的流量当量直径dL与透气率2组数据,在MatLab的工具箱中分别选用傅里叶级数拟合、三次多项式拟合和正弦函数之和这3种优选的数据拟合方法,并统计数据拟合后输出的评估参数,结果如表3所示。
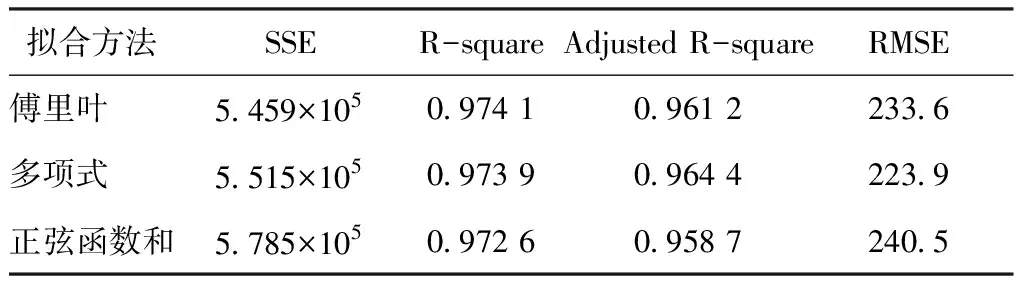
表3 3种优选方法的参数对比Tab.3 Parameter comparison of three optimization methods
根据表3中4个评估参数值,同理可得傅里叶级数和多项式拟合这2种数学模型的拟合性能更优。
3.2 2种数学模型的对比
多项式数学模型其原理是构造一个简单的函数,在某个有效区域内对有限个采样点的函数值去逼近一个复杂或者未知的函数。为了更好地避免实验引起的一些误差,可以采用最小二乘法来获得一个光滑的曲线,观察获得数据的变化规律。根据实验所测量的数据,令y为织物透气率,x为等速当量直径,组成观测量{(xi,yi),i=0,1,…,n},然后构建一个m(m≤n)次的多项式,如式(5)所示。
P(x)=a1xm+a2xm-1+…+amx+am+1
(5)
式中:a为待定系数;x为等速当量直径,mm;m为多项式的最高次幂;P为织物透气率的逼近值。
傅里叶级数的意义在于对某个未知的函数按一定的形式进行分解,从而用正弦函数的几种组合形式来正确表达,而微分运算的本质正是正弦基函数,因此求解线性微分方程可以用常数的代数来获取,其计算如式(6)所示。
(6)
式中:T为一个周期;n为周期数;a为余弦的幅度;b为正弦的幅度;x为等速当量直径,mm;P为织物透气率的逼近值。
利用2种数学模型对所测量的数据进行拟合,其误差值为δi=P(xi)-yi,设定φ0,φ1,...,φm使其在有效区间内不存在线性相关,使测量数据的误差平方和最小,其计算如(7)式所示。
(7)
式中:δ为误差值;φ为选定的函数;P为织物透气率的逼近值;y为织物透气率。
3.3 拟合计算
在3.1中用不同模型进行了2组评价参数比较,可以看出等速当量直径与流量当量直径作为数据输入偏差很小,因此尝试将实验所测量的织物的等速当量直径dh与织物透气率Q作为数据输入,绘制彼此之间的散点分布情况,再利用MatLab中的三次多项式拟合,三次多项式拟合曲线如图1所示。
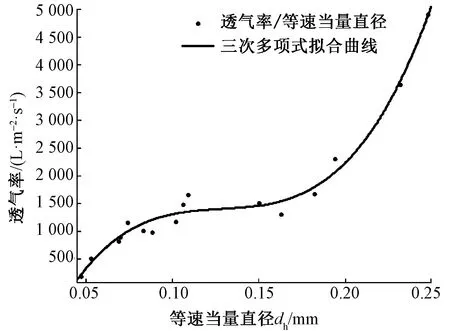
图1 三次多项式拟合曲线Fig.1 Fitting cubic polynomial curve
所得三次多项式数学模型如下:
(8)
该模型评估参数SSE为3.793×105;R-square为0.982 0;Adjusted R-square为0.977 5;RMSE为177.8。
同理,根据散点分布情况,利用MatLab对数据进行傅里叶级数拟合,展开式n取值从2至5进行,且当n大于等于6时,模型已不成立,然后比较各项式的评价参数,最终得到当n=2时所呈现的拟合曲线最为光滑,误差平方和SSE最小,如图2所示。

图2 傅里叶级数拟合曲线Fig.2 Fourier series fitting curve
傅里叶级数数学模型如下:

(9)
该模型评估参数SSE为3.684×105;R-square为
0.982 5;Adjusted R-square为0.973 8;RMSE为191.9。
散点的分布在图1、2上差异非常小,通过对实验数据中的等速当量直径dh和透气率之间的散点分布图拟合分析,可以清楚地看到其变化规律:当孔径值在0.11 mm以下时,织物的透气率随孔径的增大缓慢增加;当孔径在0.11~0.16 mm之间时,透气率随孔径的增大无明显变化;而当孔径值超过0.16 mm并不断增大时,透气率也迅速增大。
4 模型检验
重新选取5块不同织物(记为面料A~E)分别进行透气率的测定,然后根据拟合所得的2种数学模型进行织物的透气率预测,再参照(2)式和(4)式计算织物间隙孔直径dh和dL,分别代入式(8)(9)计算其透气率,以验证2种模型的正确性及可行性,5种验证织物的结构参数及测量值见表4。

表4 5种验证织物的结构参数及测量值Tab.4 Structural parameters and measured values of five kinds of verification fabrics
将2种模型预测的计算值与实测值进行相关性分析,验证所得的预测值是否准确可靠。结果表明三次多项式模型的相关系数为0.982 0,其误差范围在4.02%~10.25%,平均误差为7.40%;而傅里叶级数模型的相关系数为0.982 5,其误差范围在2.60%~11.21%,平均误差为7.06%,即傅里叶级数的二次展开模型相对更优。
5 结 论
对16种常见织物的结构参数和透气性进行实际测量,基于MatLab中的曲线模型对数据进行拟合分析,分别用不同的数学模型对实验数据进行比对分析,以输入与输出误差的平方和(SSE)、多重测定系数(R-square)、自由度调整测定系数(Adjusted R-square)和均方根误差(RMSE)为模型的评价依据,同时利用5种织物进行验证分析。最终确定傅里叶级数的二次展开模型为最佳,该模型计算值与实测值之间相关系数均达到0.98以上,预测误差范围为2.60%~11.21%,平均误差为7.06%。
傅里叶级数模型可用于分析织物透气性、纱线线密度及表观直径之间的函数关系,该方法有一定的可行性,可为面料的生产和使用提供参考。
