基于RFPA2D岩石渗流剪切破坏过程研究

胡 斌，彭锐波，崔 凯

(1.武汉科技大学 资源与环境工程学院，武汉430081；2.冶金矿产资源高效利用与造块湖北省重点实验室，武汉430081)

滑坡是我国最常见的地质灾害之一。顺向岩质边坡在降雨不良工况下，坡体结构浸水软化，抗剪强度持续降低，沿软弱结构层面发生滑动，从而引发滑坡等地质灾害[1]，故研究岩石在剪切荷载和降雨渗流耦合作用下的破坏过程具有重要的工程应用和实践意义[2]。

剪切荷载和降雨渗流作用是岩质边坡岩体发生节理贯通破坏失稳的主要诱因，已成为岩石力学领域研究的热点课题。芮勇勤等[3]模拟了岩石剪切试验，并分析了岩石从变形到破裂直至失稳的全过程；彭守建等[4-5]开展了渗透水压作用下完整砂岩剪切-渗流耦合特征试验，结果表明，在恒定渗透压条件下，抗剪强度与法向应力成正比关系，而法向和剪切位移与法向应力成反比关系；曹成[6]以浅埋深下的砂岩为研究对象，开展不同法向应力和渗透压作用下的单裂隙剪切-渗流耦合试验，结果表明，剪切过程的渗透系数会随隙宽的增大而大幅提升，但会随法向应力的增大而减小；刘才华等[7]研究了岩体在剪切荷载下的渗流特性，并对裂隙剪缩阶段过流能力的变化进行探讨，结果表明，裂隙渗透性随剪应力的增大而降低，且剪应力与渗透系数有较为明显的线性关系；唐春安等[8]、杨天鸿等[9]对孔隙水压作用下岩石加载破坏过程进行数值模拟，结果表明，孔隙水压力的梯度大小对岩石裂纹的萌生和扩展有明显影响；周辉等[10]研究了不规则锯齿形结构面在不同剪切速率及不同法向压力作用下的声发射参数特征，结果表明，试验过程的累计撞击曲线可以分为三个阶段，且能量率曲线和撞击率曲线与剪切速率成正相关关系；许江等[11]开展了不同法向应力下煤岩剪切试验；杨洁[12]开展结构面剪切渗流试验，结果表明，水力梯度与流量间为非线性关系；李鹏等[13]开展了软弱结构面在不同含水率下的剪切试验，分析了不同含水率影响下软弱结构面的剪切机制。

RFPA2D常用于模拟岩石的渐进破坏过程，特点在于可模拟岩石材料典型的非均质性，其良好的模拟效果得到了众多学者的青睐。吴钰等[14]运用RFPA2D研究了含裂隙岩石受压条件下不同倾角单、双裂隙岩样的力学性能和裂纹萌生、扩展及其破坏模式；付斌等[15]利用RFPA2D研究了不同围压、不同组合倾角条件下煤岩组合体的破坏过程，结果表明，组合体的强度与组合倾角成反比关系；刘俊杰等[16]采用RFPA模拟了采场覆岩应力场的重新分布规律，再现了采动区覆岩裂纹萌生、扩展和贯通的全过程；闫月龙等[17]运用RFPA开展了节理不同位置、方向和迹长对于岩石单轴抗压强度影响的数值模拟试验，结果表明，试件裂纹尖端到受压面距离与抗压强度值有近似线性关系。

综上所述，尽管目前在渗流剪切试验性研究方面取得了丰硕成果，但针对砂岩渗流剪切破坏过程的数值模拟仍有不足，尤其是采用数值声发射手段探讨渗流剪切下砂岩内部裂纹开裂、扩展过程仍有待进一步研究。因此本文采用RFPA2D软件开展砂岩在渗流剪切作用下破坏过程的数值试验，进行渗流剪切特性分析，从应力分布、剪切力、法向位移和声发射等方面多维度剖析砂岩渗流剪切破坏过程，得到砂岩渗流剪切破坏规律，以期为岩质边坡的防护治理提供一定的数值参考。

1 模型建立与参数选择

数值模型宽高比为1∶2，形状如图1所示，尺寸为75 mm×150 mm，总计120×240=28 800个微元，并在模型两侧中部预先分别切出33 mm的水平诱导裂纹[2]。荷载施加方式为：上部施加2 MPa的恒定法向荷载；右侧边下半区域采用位移控制剪力加载，每步0.002 mm；渗流孔底部施加2 MPa恒定渗透压，两侧渗透压设置为0 MPa(模拟现实渗流孔中水头压力为0的情况)，数值试验共加载400步。RFPA系统设定岩石的力学性质(微元的变形及强度性质)服从韦伯分布Öc(m，μ)，其中，m为形状参数(一般岩石的m取值为2～4)，反映模型力学性质的均质程度，m值愈大，表示岩石的性质越均匀；μ为反映岩石材料平均性质的参数。

图1 数值分析模型Fig.1 Numerical analysis model

RFPA2D软件计算所需的细观抗压强度值与宏观抗压强度值、细观弹性模量值与宏观弹性模量值计算式如式(1)和式(2)[8]，计算得其宏观力学参数与细观力学参数间转换关系见表1。

表1 力学参数宏细观转换表Table 1 Macro and mesoscopic conversion table of mechanical parameters

(1)

(2)

其中：E宏观为岩石宏观弹性模量；E细观为模型细观弹性模量；f宏观为岩石宏观抗压强度；f细观为模型细观抗压强度；m为均质度。

数值模拟所需物理力学参数参考岩质边坡物理力学参数[18]，取宏观抗压强度为40 MPa、宏观弹性模量为30 GPa，根据模型的尺寸，m取值为2。通过表1计算出细观抗压强度与弹性模量以及其他力学参数，如表2所示。

表2 数值模拟力学参数表Table 2 Numerical simulation mechanical parameters table

2 砂岩剪切-渗流耦合特性分析

2.1 应力分布

图2是数值模型在剪应力作用下破裂过程的应力分布图，数值模拟结果表明，模型宏观剪切裂纹带是由诸多微裂纹组成，由图2可知，微裂纹虽出现在剪切带上，但其萌生的起因为拉伸应力破坏。由图2a可知，在加载初期，法向应力高于剪切荷载，在模型中心区域形成一个椭圆形的低应力区，此区域周边各微元相继出现相变；随着剪应力的增加，模型中部区域应力场发生偏转(图2b)，沿两个预制裂纹中心区域的应力逐渐升高，各微元相变开始从预制裂纹端部相向发展，且在模型中部(加载初期的低应力区域)出现一个相变集中的区域；随着持续加载，该区域各微元力学性质弱化，模型中部的承载能力降低，并产生大量以剪切性为主的微裂纹(图2c)，大量的裂纹最终沿预制剪切面贯通，模型出现宏观裂纹。由于模型中各微元的非均质性，整个宏观裂纹呈现锯齿状，模拟结果与室内试验得到的粗糙剪切面保持一致。

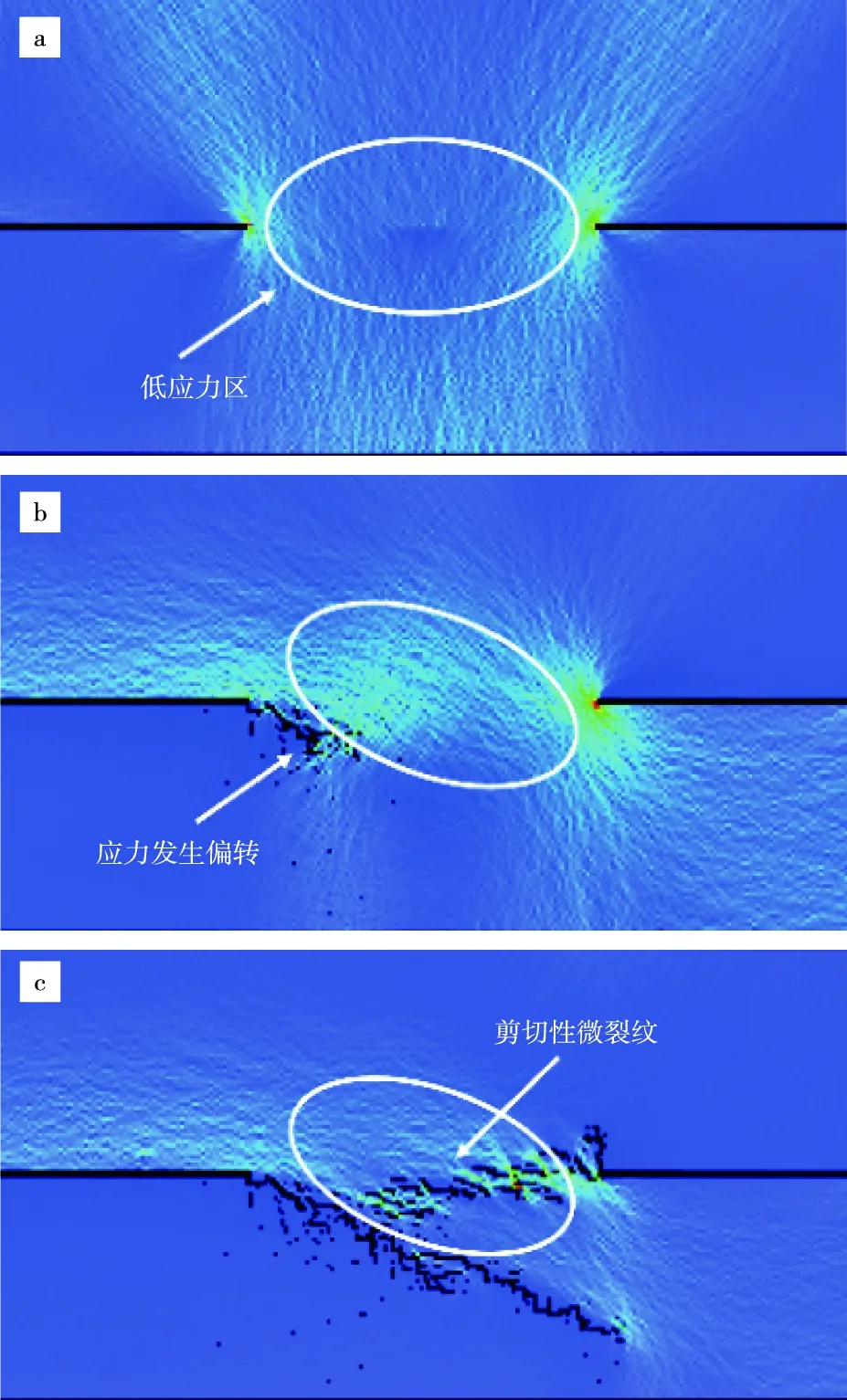
图2 渗流剪切破坏过程应力分布图Fig.2 Stress distribution diagram of seepage shear failure process

2.2 剪切应力-应变曲线

剪切应力-应变曲线如图3所示，可将试样模型的变形破坏过程分为四个阶段：稳定变形阶段、亚稳定变形阶段、失稳前兆阶段(又称极限稳定阶段)和失稳破坏阶段。加载伊始，剪应力随时间缓慢增大，剪切应力-应变曲线表现为线弹性增长(OA段)，此阶段内部微元被压密；剪切荷载持续增加，微裂纹在模型中并非完全对称(模型的尺寸是对称的)，而在模型左侧的中部区域发展较快，表现出明显的应变局部化现象，右侧亦然，剪切应力-应变曲线呈现偏离性的趋势(AB段)；荷载继续增加，微裂纹加剧明显，应力-应变曲线进一步偏离(BC段)；当剪应力超过其屈服强度，内部出现大量微裂纹，此时剪应力达到峰值点C(数值模拟第165步)，模型内部结构性遭到破坏，剪切主裂纹在预制剪切面处迅速贯通，剪应力骤降(CD段)；随着剪应变的增大，模型在残余变形阶段产生一个次级微破裂高潮(D点)，导致破裂面的抗剪强度再次降低，微裂纹的数量因应力跌落而骤减，由于剪切面的表面不规则，剪切滑动时存在摩擦力，即残余变形强度，此时模型仍具有一定的抗剪能力[19]。

图3 剪切应力-应变曲线Fig.3 Shear stress-shear strain curve

2.3 法向变形-加载步曲线

法向应力为2.0 MPa条件下，模型的法向变形-时间曲线如图4所示，在进行剪切-渗流耦合数值模拟时，由于在建模过程中约束了模型的边界，其侧面的变形可忽略不计，即ε2=ε3=0，所以，在剪切过程中，模型限定只发生法向变形ε1，以法向应力来反映剪胀和剪缩现象。如图4(a)所示，加载初始阶段，法向应变几乎没有变化，近似水平，剪缩现象不明显；进入稳定变形阶段，法向应变开始“正向增大”，这是由于模型下部区域受剪应力作用产生相对滑动，沿趋势剪切面滑动时需克服微元间的摩擦阻力而发生挤压错动，产生法向正位移，由剪缩演变为剪胀。随各微元间持续挤压错动，剪胀效应愈加明显，法向变形持续正向增大，至此进入非稳定破裂发展阶段，法向变形不稳定，直至数值模型发生剪切失稳破坏，模型失稳破坏后法向变形骤减，这是由于剪切面的不规则性造成的。

数值模型的法向变形-时间曲线局部放大(0～50步)如图4(b)所示，加载初期，法向变形“负向变大”，在M1达到最大负变形，由于在数值试验初期，法向应力对内部微元影响更大，模型试样逐渐被压实压密，导致裂隙闭合，表现为剪缩效应；进入稳定变形阶段，此时剪切应力较法向应力对模型内部微元影响更大，出现剪胀现象，法向变形持续正向增大，在M2点处回归法向应变为0的状态，之后，剪胀现象更加明显，法向变形持续正向增大，直至模型被剪切破坏。

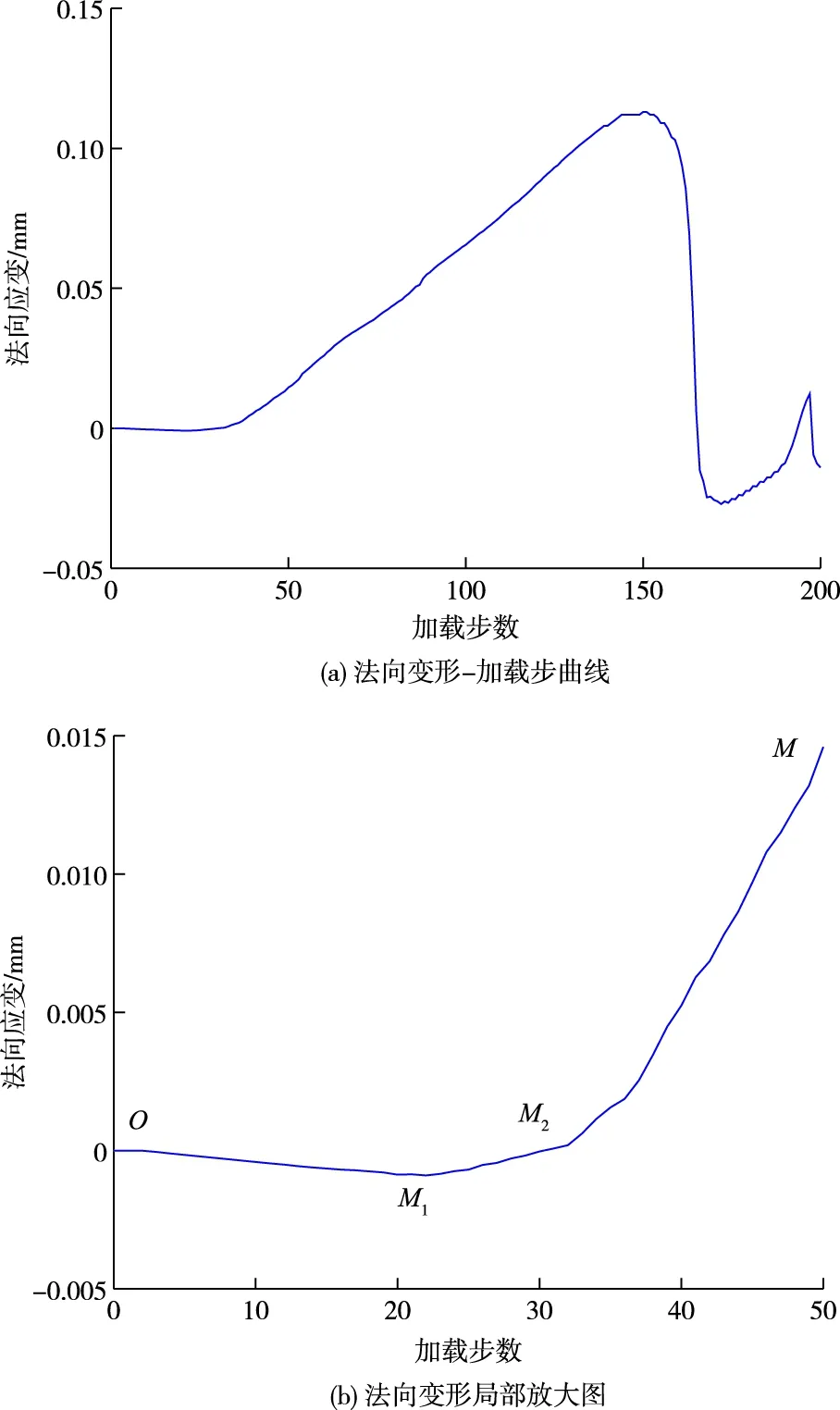
图4 法向变形-时间曲线Fig.4 Normal deformation-time curves

2.4 破裂面位移应力特征

破坏瞬间(第165步)模型中心垂线上(建模时垂向共120个网格微元)的应力曲线见图5。在破坏阶段，随着荷载的增加，预制剪切破裂面附近微元处于应变局部化阶段，模型中部产生剧烈的应力波动，由图5可以看到，中心垂线上正应力随深度的加深逐渐增大，并在69网格深度时达到最大，与数值模拟应力破坏图的裂纹位置一致(图2c)，且此处剪应力为中心垂线上的最大剪应力，表明此处局部微裂纹贯通形成剪切破裂面—滑动面。

图5 破坏瞬间模型中心垂线应力分布曲线Fig.5 Stress distribution curves of the vertical line of the model center at the moment of failure

3 声发射特性分析

3.1 裂纹扩展与声发射活动的时空演化

综合分析裂纹扩展图和声发射图(表3)可知，在第30加载步之前，模型微元保持稳定变形，在第30加载步时，模型左侧诱导裂纹端部微元出现微量拉伸性破坏，同时伴随极少声发射事件的产生(红色圆圈代表当前步拉伸性破坏引起的声发射情况，黄色圆圈代表当前步剪切性破坏引起的声发射情况)，此时右侧诱导裂纹端部出现应力集中的现象，但并无微元破坏及声发射事件产生；第30步到第73步，模型沿着拉伸微破坏方向继续产生少量拉伸性和剪切性微裂纹，此阶段对应声发射图中黄色圆圈多于红色圆圈，说明此阶段剪切性微裂纹数量多于拉伸性微裂纹数量，到73步时微裂纹方向与预制剪切面成22°夹角，此时在右侧诱导裂纹端部出现少量剪切性破坏引起的声发射事件，表明模型微元逐渐开始发展剪切性微裂纹；第73步到147步，模型沿着右侧诱导裂纹端部出现少量断断续续的剪切性微裂纹，此时出现宏观裂纹的雏形，对应声发射图中出现少量剪切性破坏引起的声发射事件，同时，声发射事件数的轨迹也可以预测宏观裂纹的走向；第147步到165步，上一阶段出现的剪切性微裂纹逐渐汇合，并与左侧诱导裂纹端部延伸出来的微裂纹相接，两条微裂纹逐渐扩展演化为显裂纹，此阶段声发射活动骤增，对应声发射图中沿裂纹汇合轨迹出现大量声发射事件，两条显裂纹持续扩展并交汇贯通，形成宏观破裂面。

表3 裂纹扩展与声发射活动对照表Table 3 Comparison table of crack growth and acoustic emission activity

(续)

由上述分析可得，模型的声发射活动在显裂纹出现之前有异常的汇聚现象；第1到第73步，声发射事件由拉伸性微裂纹和剪切性微裂纹共同作用产生，第73到165步，声发射事件则主要由剪切性微裂纹萌生扩展产生。

3.2 声发射特征参数曲线分析

图6所示为RFPA2D模拟下砂岩渗流剪切声发射特征参数(AE能量、AE累计能量和AE累计事件数)随加载步变化的演化图。由图6可得，在160步之前，声发射能量平静地维持在一个低水平，AE累计事件与AE累计能量也小幅缓慢上升，这是由于模型内部在此阶段不断产生少量微裂纹；之后AE能量较之前骤增，AE累计事件与AE累计能量也出现异常陡增现象，这是由于模型中分布的微裂纹汇合连通，形成宏观破裂面。图6中的声发射特征参数显示，AE累计事件曲线先于AE累计能量曲线出现异常增大现象，之后达到剪应力峰值，模型开始发生失稳破坏，故可将前者异常增大的时间点作为模型破坏前兆的时间点。

图6 砂岩声发射能量、声发射累积能量、累计声发射事件与加载步数关系图Fig.6 The relationship between sandstone acoustic emission energy，accumulated acoustic emission energy，accumulated acoustic emission events and the number of loading steps

4 结论

1)通过砂岩渗流剪切数值模拟，发现其变形与破坏过程存在“稳定变形”、“亚稳定变形”、“失稳前兆”以及“失稳破坏”4个基本阶段。

2)加载初期，模型的中心区域形成一个椭圆形的低应力区，持续加载，低应力区发生偏转，左侧诱导裂纹端部开始产生局部剪切性微裂纹与拉伸性微裂纹，此后，伴随预制裂纹区域应力升高，右侧诱导裂纹端部逐渐产生大量局部剪切性微裂纹，在165加载步后，拉伸性裂隙与剪切性裂隙汇合形成贯通破裂面。

3)砂岩的声发射活动贯穿整个渗流剪切破坏过程，整体表现为在峰值剪应力前，声发射特征参数水平较低，AE能量较弱，AE累计能量与AE累计事件数曲线缓慢上升，而在剪应力峰值后各项声发射特征参数骤增。研究表明，声发射信号能较好地反映砂岩渗流剪切过程中的裂纹扩展规律。