低模量合成纤维对混凝土基本徐变的影响

2022-07-13李天伦吴永根吴豪祥

空军工程大学学报 2022年3期

李天伦，吴永根，吴豪祥

(1.空军工程大学航空工程学院，西安，710038；2.中国人民解放军94831部队，福建武夷山，354300)

徐变是混凝土自身固有的性能，徐变会引起预应力混凝土结构的预应力损失、长期变形和内力重分布的显著增加，对安全性和耐久性造成严重影响[1-2]，其自发现以来就引起了人们的高度重视。

在混凝土中掺入适量的纤维能够很好地提升混凝土的使用性能，提高混凝土的强度，纤维混凝土作为一种新型复合材料已经广泛应用于道路、桥梁、隧道和建筑等[3-4]。关于纤维混凝土徐变的研究最早主要针对钢纤维，1989年Chern等对钢纤维对混凝土徐变的影响进行了试验，试验结果表明，随着纤维体积掺量的增加，徐变有所降低[5]。近年来，随着高性能合成纤维混凝土的发展，徐变相关研究逐渐增多。于俊超等研究了钢纤维和聚丙烯纤维混凝土的徐变特点，认为聚丙烯粗纤维只能改善混凝土的延性，无法抑制混凝土的徐变[6]。王玉清等测试了不同掺量聚乙烯醇纤维的混凝土徐变，测试数据表明，聚乙烯醇纤维体积含量在0.5%～2.0%范围时，纤维混凝土的徐变均大于普通混凝土，且徐变随纤维掺量的增大呈现两头大中间小的趋势[7]。已有研究表明，高模量纤维对混凝土的桥接作用比较明显，可以提高混凝土开裂后的韧性和抗冲击性能，并已被证明能够有效地减小混凝土的徐变[8]。目前已有较多模型可用于预测混凝土的徐变效应，如CEB-FIP模型[9]、GL-2000模型[10]、ACI-209模型[11]、GL-2000改进模型和B3模型[12]等。除此之外，Zhang则基于cox的剪滞理论，提出了在普通混凝土基本徐变基础上乘以纤维填充因子作为纤维混凝土徐变的预测公式，但该表达式只适用于高模量纤维混凝土，并不能满足低模量纤维混凝土[13]。虽然目前已有较多模型可对混凝土徐变进行预测，但由于各模型考虑因素不同，使上述模型之间存在较大区别，其对混凝土徐变计算适用性仍需进一步探讨。

可以看出，针对合成纤维混凝土徐变的研究，目前还处于起始阶段，试验数据不够充分，也没有完整的理论，尤其是对于低模量合成纤维对混凝土徐变性能的影响仍缺乏研究。为此，本文选取清华大学生产的低模量合成纤维，研究了不同掺量低模量合成纤维对混凝土基本徐变的影响，并将试验结果与混凝土徐变预测模型计算结果进行了比较，希望能为低模量合成纤维混凝土徐变预测模型的应用提供参考。

1 材料与试验

1.1 材料

普通混凝土的配合比见表1，编号为F0。其中，水泥为42.5级普通硅酸盐水泥；粗集料为石灰石，采用5～10 mm、10～20 mm和20～40 mm 3个级配，按照1∶3∶6的质量比进行配制；细集料为河砂，细度模数为2.7；水为普通自来水。在普通混凝土中分别掺入0.8 kg/m3、1.2 kg/m3和1.6 kg/m3的纤维即可得到相对应的纤维混凝土，工作性能试验结果见表2，编号分别为F8、F12和F16。

表1 普通混凝土配合比单位：kg/m3

表2 混凝土试件工作性能试验结果单位：s

本文选取的低模量合成纤维为清华大学国家“863”研究项目中的新型高性能合成纤维见图1，纤维的具体性能指标见表3。

图1 新型高性能合成纤维

表3 低模量合成纤维技术指标

1.2 试验方法

1.2.1 力学实验

参照《水工混凝土试验规程》[14]，成型3组150 mm×150 mm×150 mm的立方体试样，24 h脱模后移入标准养护室，达到28 d龄期后测量其抗压强度。

1.2.2 徐变试验

参照《水工混凝土试验规程》[14]，每个配合比制作3个徐变试样和2个补偿试样，试样规格为Ф150 mm×450 mm。混凝土试样浇筑振捣完成后，24 h进行脱模，并用紫铜皮密封以达到绝湿状态，充气法检查密封性后移入(20±2)℃的徐变室。徐变仪器为弹簧式压缩徐变仪，加荷龄期为28 d，加载荷载为对应龄期同尺寸试件轴心抗压强度的 40%。量测设备为DI-25型差动式电阻应变计，加荷设备为油压千斤顶，在加载后第1 d、7 d、30 d和90 d各调荷一次。

采用徐变度、徐变系数以及单位应力下的总压缩应变来评价混凝土的徐变性能。其中，徐变度是指单位应力下的徐变变形，为徐变应变与持荷应力之比；徐变系数是指在恒应力作用下，试件某一时刻的徐变变形与其加载时刻的瞬时弹性变形的比值；单位应力下的总压缩应变是指单位应力下的徐变变形与弹性变形之和，按式(1)[11]计算。

εc′=(1/Ec)+Cc

(1)

式中：εc＇为单位应力下的总压缩应变，10-6；1/Ec为单位应力下的弹性变形，10-6；Cc为徐变度，10-6/MPa。

2 试验结果分析

2.1 纤维掺量对混凝土力学性能的影响

F0、F8、F12和F16试样28 d的立方体抗压强度分别为42.61 MPa、42.82 MPa、43.50 MPa和42.25 MPa，可以看出立方体抗压强度呈现先增大后减小的变化趋势，F12的立方体抗压强度最大，F16的立方体抗压强度较F0略有下降，但影响幅度均在2%以内，说明该种纤维的掺入对混凝土28 d的立方体抗压强度影响较小。

根据立方体抗压强度与轴心抗压强度的关系，换算系数取为0.53，各组混凝土试件轴心抗压强度和加载荷载如表4所示。F0、F8、F12和F16的弹性模量分别为41.0 GPa、41.9 GPa、43.5 GPa和37.9 GPa，虽然也呈现先增大后减小的变化趋势，但影响幅度均不超过8%，掺入纤维的混凝土试样弹性模量与空白混凝土偏差较小。

表4 28 d轴心抗压强度和加载荷载单位：MPa

2.2 纤维掺量对混凝土徐变的影响

徐变度、徐变系数以及单位应力下的总压缩应变随时间变化的曲线，见图2～4。

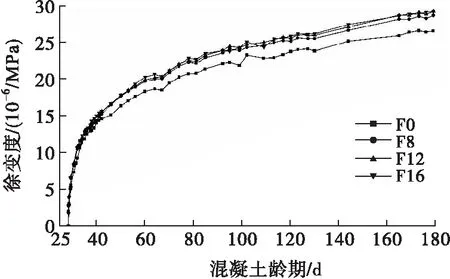
图2 徐变度

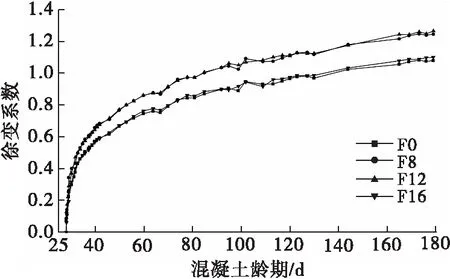
图3 徐变系数

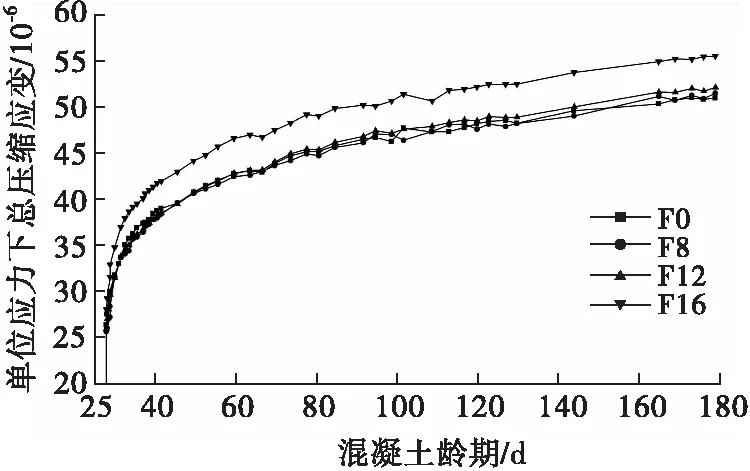
图4 单位应力下的总压缩应变

由图2可以看出，随着龄期的增长，混凝土的徐变逐渐增大，呈现出前期快后期慢的增长趋势，这是因为混凝土承受荷载时，水泥浆体的徐变与加荷应力成正比，早期徐变发展较快，而后骨料会阻碍水泥浆体的流动，加载应力逐渐转移到由骨料来承受，导致徐变速率逐渐减小[15]。F8、F12和F16的最终徐变度相比于F0分别增加了7.9%、10.1%和10.0%，表明低模量合成纤维的掺入增大了混凝土的徐变变形，主要原因是纤维的掺入增加了混凝土内部缺陷，加载状态又造成凝胶吸附水和层间水迁移和渗出，延缓混凝土的水化[16]。低模量合成纤维不能像钢纤维一样抵抗混凝土的变形，从而增大了混凝土徐变。但在试验纤维掺量范围内，由于在加荷的往复过程中由纤维引起的部分孔隙被压实，导致F12和F16的徐变差距不大。

由图3可以看出，F8、F12和F16的徐变系数相比于F0分别增大了15.3%、17.2%和1.9%，在徐变度差异不大的情况下，说明F16和F8、F12的弹性变形差异明显，F8和F12的弹性变形较F0分别减小了15×10-6、19×10-6，F16的弹性变形较F0却增大了5×10-6，主要原因是合成纤维在混凝土中形成了较好的三维搭接结构，改善了微观结构，提高了混凝土的韧性，但是过大的掺量导致纤维的重叠交织，对混凝土界面的弱化作用增强，增大了混凝土被“压密”的可能性，对于混凝土基体而言是一种不容忽视的缺陷[15]。

由图4可以看出，F8、F12和F16单位应力下的总压缩应变相比于F0分别增加了1.1%、2.3%和8.9%，其相对大小关系与图2有明显差异，其原因在于徐变系数是以“除”的形式引入弹性变形，而单位应力下的总压缩应变则是以“加”的形式引入弹性变形。F8、F12和F0的变化曲线基本重合，表明掺量在0.8～1.2 kg/m3范围的低模量合成纤维虽然能提高混凝土的抗压承载能力，但无法提高混凝土抵抗长期压力变形的能力，而1.6 kg/m3的纤维掺量明显降低了混凝土抵抗长期压力变形的能力。

纤维对混凝土基本徐变的影响主要体现在两个方面，一是对混凝土内部结构的影响；二是发挥混凝土内部变形的“阻挡”作用。纤维的掺入会增大混凝土的内部孔隙率[17]，增加混凝土内部的“多害孔”[18-19]，这些较大孔隙对混凝土基本徐变的影响随时间变化呈现两种作用，一是在加荷过程中孔隙增多给孔壁两侧C-S-H的滑移提供了更多的可能，同时会产生更多的初始微裂缝和缺陷，微裂缝会引起混凝土内部湿度的不平衡，导致毛细孔周围的水分向毛细孔移动，进而引起周围的水泥浆体干燥收缩，增大混凝土变形，而缺陷则会降低混凝土抵抗变形的能力；二是随着水泥的进一步水化，混凝土中的孔隙逐渐变小，当缩小到毛细孔大小后，水泥的继续水化便会引起混凝土进一步的收缩变形[20]。因此，在同等应力水平下，该种低模量合成纤维的掺入增大了混凝土的徐变。

3 徐变预测模型对纤维混凝土徐变的适用性

针对混凝土徐变的预测模型较多，使用广泛的有双幂函数模型、幂函数模型、对数函数模型和指数函数模型[21]，针对混凝土基本徐变的主要有CEB-FIP模型和GL-2000模型。本文将测试结果与上述模型拟合结果进行对比，其中，双幂函数模型采用ACI-209R模型，对数函数模型采用CEB-FIP模型，GL-2000模型公式乘以修正系数m。拟合结果见表5，拟合曲线见图5～8。

表5 徐变系数拟合曲线相关参数

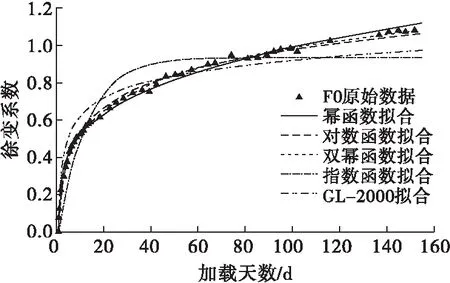
图5 F0徐变系数拟合图

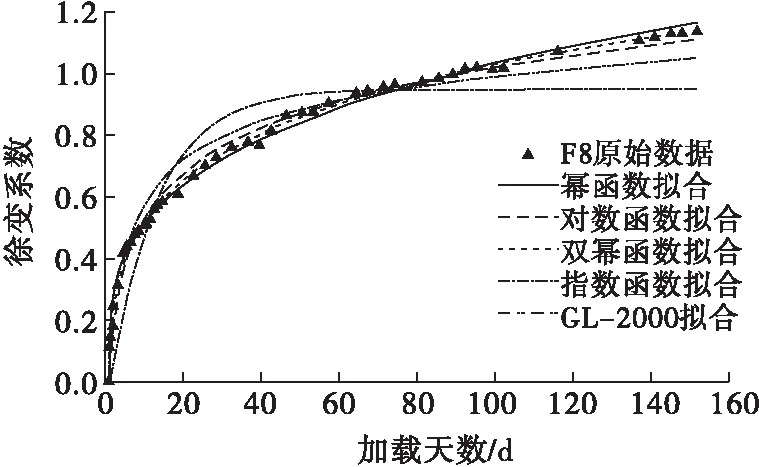
图6 F8徐变系数拟合图

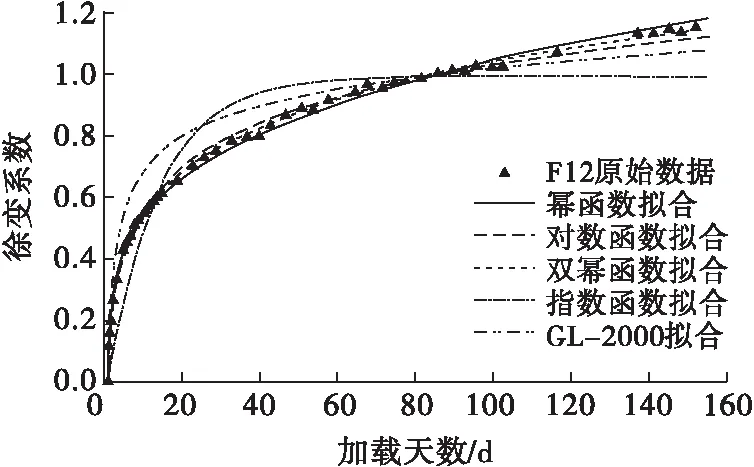
图7 F12徐变系数拟合图

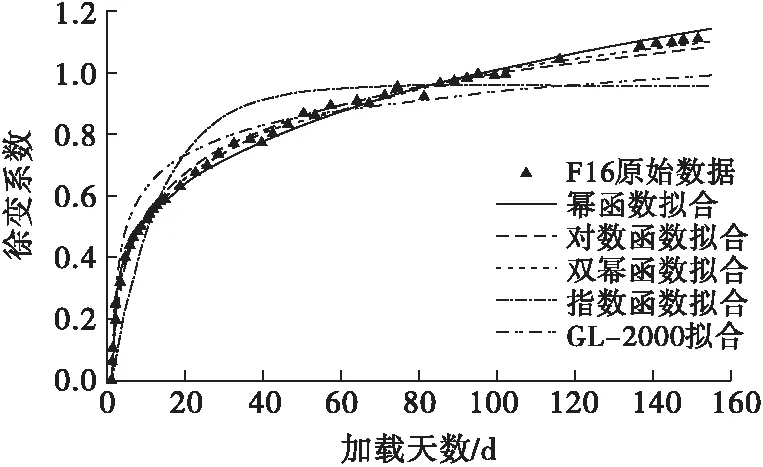
图8 F16徐变系数拟合图

由拟合曲线可以看出，对于混凝土前180 d龄期的徐变，双幂函数的拟合效果最好，R2均大于0.997；对数函数和幂函数也有较好的拟合效果，R2均大于0.990，但对数函数后期曲线有低于实际曲线的趋势，而幂函数后期曲线则有高于实际曲线的趋势；指数函数的拟合效果最差，不适宜作为预测函数。GL-2000模型拟合后R2均大于0.92，拟合效果也不错。根据拟合结果，本文对ACI-209R、CEB-FIP和GL-2000这3个模型的适用性进行进一步分析。

ACI-209R模型公式中，参数a为最终徐变系数，应在1.30～4.15范围内；参数b和c是从试验中获得的拟合数据，应分别在6～30 d和0.40～0.80范围内。虽然该公式主要针对混凝土的总徐变即基本徐变和干燥徐变之和，但根据拟合效果，其在基本徐变数据拟合上仍有很好的效果，且回归参数值均在合理范围内，因此认为ACI-209R可以作为低模量合成纤维混凝土徐变的预测模型。由于其相关参数无法根据材料性能和环境等进行计算，需要通过短期测试数据进行回归。本文分别利用前14 d(16组)、前60 d(26组)和前100 d(38组)数据进行回归，结果表明，F0、F8、F12和F16后续徐变系数的最大相对误差均在7%以内，预测效果很好。

CEB-FIP模型公式按式(2)[13]计算。

(2)

式中：φbc为时间增长函数；fcm为混凝土28 d龄期的强度；t0,adj为调整后的龄期。

同样，分别利用前14 d(16组)、前60 d(26组)和前100 d(38组)数据进行回归，结果表明，F0、F8、F12和F16后续基本徐变度的最大相对误差分别为17%、12%、9%和6%。

对于GL-2000模型公式，当修正系数m=1(即采用原公式)时，能够直接计算混凝土的徐变系数，但60 d后的徐变系数，F0、F8、F12和F16的最大相对误差分别为11%、12%、13%和12%。可以看出，GL-2000直接预测混凝土的徐变系数有较大的误差，即使采用前100 d(38组)数据进行回归，其后续徐变系数最大相对误差仍达到了15%，因此认为GL-2000模型不适合用于低模量合成纤维混凝土徐变的预测。