多层速度格子Boltzmann 方法进展及展望

杨 鲲，单肖文

(1. 南方科技大学 前沿与交叉科学研究院，深圳 518055；2. 南方科技大学 工学院 力学与航空航天系，深圳 518055)

0 引 言

诞生于格子气自动机[1]的格子Boltzmann 方法（LBM），与传统直接求解宏观量的计算流体力学（CFD）方法相比，由于避开了Navier-Stokes 方程非线性项的处理，且没有求解压力泊松方程这一繁重过程，使得LBM 具有程序编制简单、并行计算效率高的优点[2]，在湍流、多相流、多孔介质流动及渗流、颗粒流、微流动、气动声学等领域的模拟中得到了广泛应用[3-6]。早期的LBM 离散模型都是基于半经验理论推导，其约束条件往往局限于满足质量和动量守恒方程，并以低马赫数假设为基础，能量方程无法正确还原，使得LBM 方法只适用于等温低速弱可压流动成为了较普遍的观点[2，7]。

随着航空航天科技发展，高速流动的数值模拟在飞行器设计验证中起到越来越重要的作用[8]，CFD 领域涌现了多种可压缩流动的处理格式与方法，例如黎曼问题求解器和TVD 格式[9]、用于高精度激波捕捉的WENO 格式[10]，以及计算激波-湍流相互作用的Compact-WENO 混合格式[11]；这些数值方法在理论研究和工程应用领域都取得了可观的成果[12-13]。不可否认的是，尽管传统CFD 方法已经过了多年的发展和完善，在具体问题中要同时准确解析流动小尺度结构和激波间断，实现模拟方法的精度、耗散、稳定性和计算效率等因素的最佳平衡，仍然存在着诸多挑战[14]。另一方面，工程传热流动问题中，高效换热器普遍具有形状复杂的管腔结构，处理复杂几何边界、并兼顾精度和计算效率也对流动模拟方法提出了更高的要求。

LBM 源自于气体动理学理论，对气体运动描述的物理背景清晰，且在处理复杂几何外形、特别是多孔结构时具有独特优势，理论上LBM 在模拟可压缩流动和复杂结构的传热流动问题方面拥有巨大潜力。研究者们对传统LBM 模型进行了诸多改进，以期突破LBM 在计算可压缩流动和热力学流动时的局限性，其基本思想是增加LBM 离散模型的自由度和约束条件以还原能量守恒方程。改进方案大致分为两类，一类是额外增加一个能量（内能或总能）分布函数以满足能量方程约束[15-20]，称之为双分布函数模型。然而，根据气体动理学理论，气体的密度、动量和能量都是气体分子热运动的统计结果，其动力学状态也应当只需由单一的分布函数描述（对于单组分、单原子气体而言），因此引入能量的分布函数必然需要与密度分布函数进行耦合，该耦合关系带有一定的经验性，在增加复杂度的同时也对模型的广泛适用性带来了一定的限制。另一种方案是构造更高阶的单一平衡态分布函数，在平衡态分布函数中引入更多的待定系数，并使用更多的离散速度点，通过增加离散点数量（未知数个数）的方案来满足额外的能量方程约束，典型做法是在每个离散速度方向上使用2 个以上的速度大小模态，称之为多层速度模型。与双分布函数模型类似，多层速度模型在能量方程约束条件、分布函数的形式和离散速度点选取上也具有一定的经验性，自Qian[21]和Alexander 等[22]提出以来，出现了形式多样的方案且各有优缺点。

多层速度模型按平衡态分布函数展开式的构造方法主要分为三类：第一类遵循传统LBM 模型的思路，将Maxwell-Boltzmann 分布函数泰勒展开至更高阶数[23-26]。第二类由Shan 等[27]提出，他们发展了Grad[28-29]的早期工作思路，认为平衡态分布函数可由Hermite 多项式级数展开，只需要将展开级数保留足够的截断阶数，即可分别还原到Navier-Stokes 方程的质量、动量和能量方程，而密度、动量、能量等宏观统计量均可由Hermite 展开式的各阶系数组合表达，并在进一步的工作中阐明传统等温弱可压LBM是Hermite 多项式模型的低阶形态，且离散速度是五阶精度Gauss-Hermite 积分公式的积分点的事实[30]。第三类由Xu 等[31]提出，其基本思想是不预设平衡态分布函数的展开形式，而是将离散模型还原质量、动量和能量方程的约束条件视为平衡态分布函数离散点的线性代数方程组，直接求解方程组得出离散分布函数。

由于Maxwell-Boltzmann 分布函数的各阶Hermite多项式展开是确定的，Gauss-Hermite 积分公式的积分点也具有确定性，使得上述第二类基于Hermite 多项式构造的多层速度模型不依赖于经验而具有普适性。然而，由于该模型的数学基础理论较为晦涩，各部分细节的阐述散落于跨度接近20 年的多篇文献中，使得科研工作者对该模型进行深入理解存在一定的困难。为了弥补这个缺点，使读者连贯、系统地理解Hermite 多项式模型的构造原理和方法，同时也在与其他LBM 模型的对比中全面认识各类方案的优劣，我们对Hermite 多项式模型重新梳理归纳的同时，也一并列出了其他多层速度模型的构造思想，作为LBM 多层速度模型的一个简要总结性工作。

本文的各部分内容为：第1 节为Boltzmann 方程和LBM 的基础理论。由于多层速度模型起源于经典的等温弱可压LBM，且经典LBM 模型的很多思想在多层速度模型中仍然适用，故第2 节对等温弱可压LBM 进行简单介绍。第3 节介绍各类多层速度LBM模型（除Hermite 多项式模型以外）的基本思想。第4 节详细描述Hermite 多项式模型的理论和平衡态分布函数的具体形式，以及基于Gauss-Hermite 积分公式的离散速度模型及其构造方法。第5 节对LBM 和传统CFD 方法的结合进行了简要介绍，例如LBM 有限差分、LBM 有限体积和LBM 有限元方法。第6 节对现有的多层速度模型存在的问题进行总结，并提出未来需要完善和发展的方向。

1 Boltzmann-BGK 方程

由于无量纲化的Boltzmann-BGK 方程和平衡态分布函数分别与式（10）和式（11）形式上完全一致。因此

2 等温弱可压LBM 模型

等温弱可压LBM 模型是最早提出的LBM 模型，并在不可压流动计算中得到广泛应用。严格意义上，包括气体、液体在内的所有流体都具有可压缩性，例如液体的压缩性可用Tait 方程描述[34]。传统求解压力泊松方程的不可压流计算方法将导致无限大声速，也就是压力扰动的无限速度传播，这与物理事实是相悖的。采用弱可压方法计算“不可压流动”理论上更加接近物理本质。本节对等温弱可压LBM 模型进行简要陈述，这也将成为多层速度LBM 模型修正和拓展的基础。

2.1 速度空间离散模型

图1 等温弱可压流动LBM 的一维和二维离散速度模型Fig. 1 One- and two-dimensional discrete velocity models for isothermal weakly compressible flows

2.2 时间和空间离散

3 多层速度LBM 模型

从第2 节可以看到，等温弱可压流动LBM 模型，其离散速度在每个方向都只有一个值（分布函数信息只传播到相邻的网格点），因此称之为单层速度模型。推导该模型时，只约束了离散模型的质量、动量和动量输运量，故无法准确还原能量方程。受此启发，业内学者开始对离散模型施加能量相关（f(0)的ξ三阶以上矩）的约束条件，伴随而来的是更高阶的f(0)展开式和更多的离散速度点，其中普遍做法是在各离散速度方向上采用2 个以上的速度值（模态），因此这些模型称之为多层速度模型。本节对几类较为典型的多层速度模型进行简要陈述。

3.1 早期多层速度模型

图2 Qian 的二维离散速度模型[21]Fig. 2 Two-dimensional discrete velocity model of Qian[21]

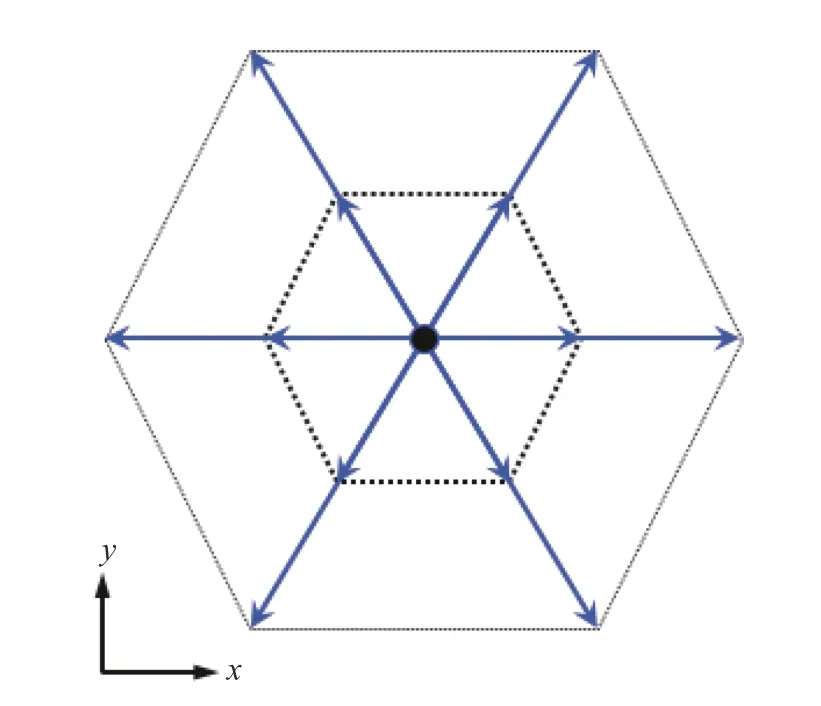
图3 Alexander 等[22]的二维离散速度模型Fig. 3 Two-dimensional discrete velocity model of Alexander et al[22]

3.2 Watari-Tsutahara 模型

3.3 比热可变模型

图4 Chen 等的二维多层速度模型[23]Fig. 4 Two-dimensional discrete velocity model of Chen et al.[23]

图5 Watari-Tsutahara 二维多层速度模型[24-25]Fig. 5 Two-dimensional discrete velocity model of Watari-Tsutahara[24-25]

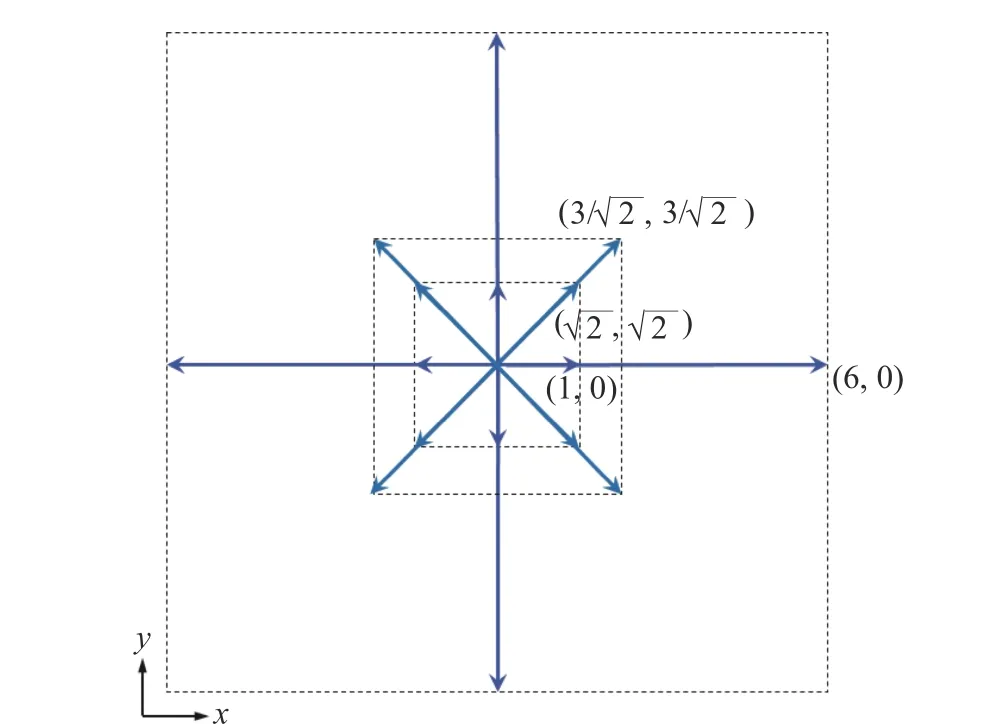
图6 Kataoka-Tsutahara[26]二维多层速度模型，图中的坐标代表离散速度点ξ a/cs在第一象限的坐标Fig. 6 Two-dimensional discrete velocity model of Kataoka-Tsutahara[26]. Coordinates represent the discrete velocities in the first quadrant

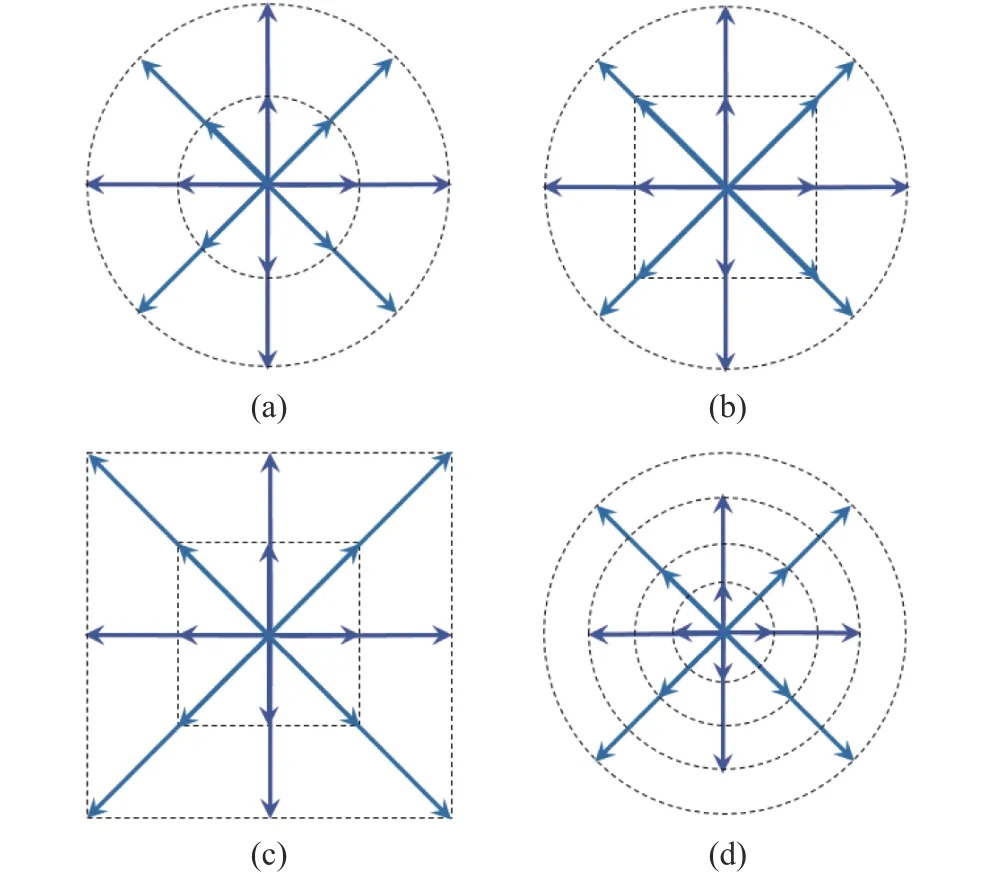
图7 离散Boltzmann 方法的几种二维离散速度模型[39]Fig. 7 Several two-dimensional discrete velocity models in DBM[39]

4 Hermite 多项式模型

4.1 速度空间展开

从第3 节的介绍可以看出，大部分多层速度模型还是沿袭了单层速度模型“预设平衡态分布函数离散形式—预设离散速度模型—待定系数法求解”的思路。这种思路可以针对每一类特定问题都构造相对优化的多层速度模型，但经验性较强，对于开始接触多层速度模型的学者而言，面对种类繁多的离散模型、平衡态分布函数形式和约束条件，如何选择最优方案往往无所适从；即便获得了对某一问题的优化组合，当流动参数改变后，计算结果不一定同样令人满意，无法保证模型的普适性。

Shan 等[27,30]在Grad[28-29]工作的基础上，发展了Hermite 多项式模型，该模型基于Hermite 多项式级数展开的数学性质，使平衡态分布函数的展开形式和离散速度模型都不再依赖于经验而具有确定性，且可以证明单层速度模型事实上是多层速度模型的低阶形态。这正是本节将详述的内容。

参照Grad 的定义，D维空间的n阶Hermite 多项式定义为n阶张量：

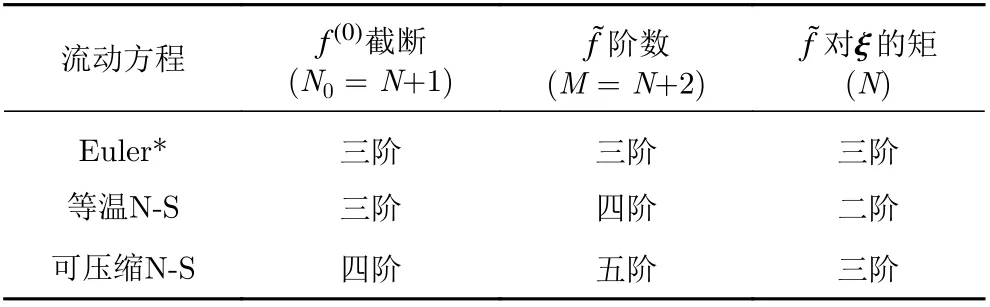
表1 不同流动分布函数的Hermite 截断式最低阶数Table 1 Lowest order of truncated Hermite distribution function for different types of flows

4.2 时间和空间离散

4.3 离散速度模型

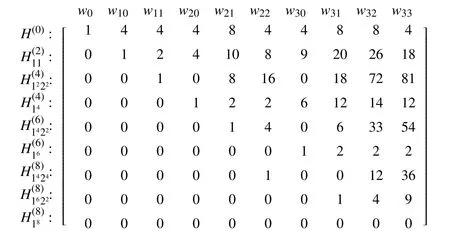
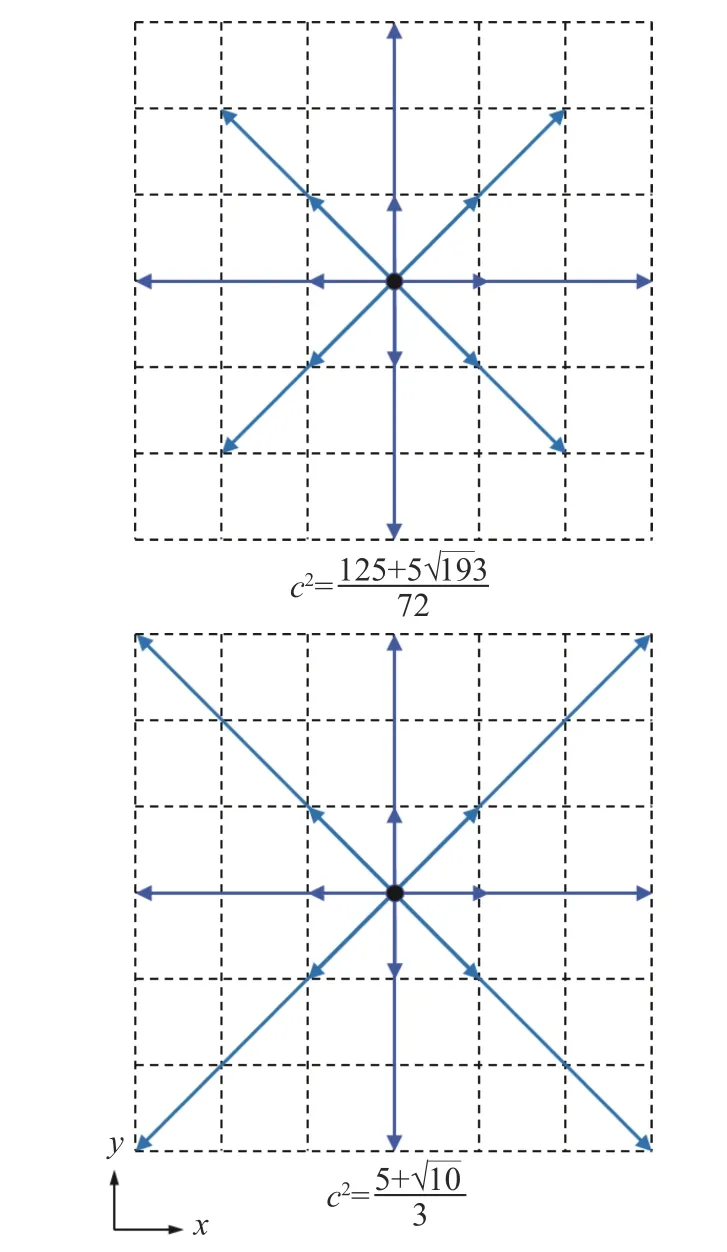
图8 2 种D2V17 离散速度模型Fig. 8 Two types of D2V17 discrete velocity models

在之前的讨论中，有一个重要的问题没有展开——如何获得具有K阶精度的数值积分公式（式点序列要保留表2 中列出的至少2 个8 积分点组，其总积分点数最少为 1+4×5+8×2=37。若保留表2中的前8 组积分点组与权重，则得出与Pillippi[51]相同的D2V37 模型，如图9 所示。

表2 二维积分公式的积分点与权重Table 2 Quadrature abscissas and weights of the 2D integral formula

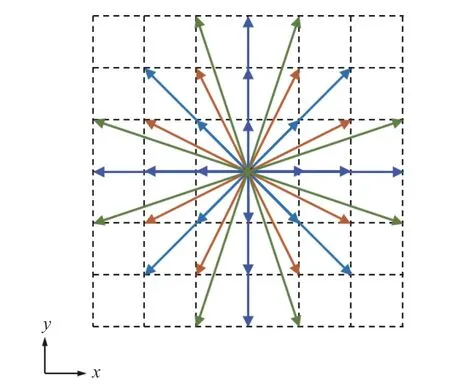
图9 D2V37 离散速度模型Fig. 9 D2V37 discrete velocity models

对于三维情况下的积分公式，也可以遵循同样的思路求解。相关的细节过程可参考文献[47]。

4.4 等温弱可压模型的推导

5 与传统CFD 方法的结合

经典的LBM 中时间和空间离散均为沿特征线积分（参考2.2 节和4.2 节），并设置归一化的 Δt=1，这极大简化了LBM 的计算程序。然而这种时空离散方法也带来了几个弊端：

1）由于 Δx为固定值，只能采用均匀正方形（体）网格。对于边界层流动计算而言，为了解析边界层内的流动而加密全计算域网格会极大增加计算量。在计算量和解析度之间取平衡的办法是使用局部加密网格，但是粗网格和细网格之间的插值会带来新误差[52]。

2）无法使用贴体网格。在倾斜方向边界，或者曲面边界上，需要同时使用笛卡尔网格和浸没边界法[53]，以锯齿形边界近似斜边界或者曲面边界。这种非贴体网格由于精度较低，且在对流扩散问题中易造成收敛性困难[54]和稳定性问题，往往需要与局部加密网格和多松弛时间模型（MRT）结合[55]。

3）计算稳定性。经验表明，经典LBM 方法在雷诺数较大时只能使用较小的物理时间步长才能获得稳定的数值解；当使用Zhou-He 非平衡态反弹边界条件[56]时稳定性问题更加突出，这对实际工程湍流的计算会形成较大的障碍。

由于传统CFD 方法可以使用边界层加密贴体网格，使用合适的时间与空间格式时，数值稳定性良好，将传统CFD 方法与LBM 结合成为了解决以上问题的一种思路。Reider 和Sterling[57]、Cao 等[58]将有限差分法与LBM 模型结合，提出了FDLBM 方法。FDLBM 的基本思路是将LBM 方程（式（104））视为关于各个离散分布函数fa的双曲型方程，通过有限差分法的时间离散格式，例如Euler 格式或者Runger-Kutta 格式，将 ∂fa/∂t离散化；并使用迎风型或中心型格式将对流项 ξa·∇fa进行空间离散[59]。在可压缩问题中，需要将多层速度模型和激波捕捉差分格式结合。Kataoka 和Tsutahara[26]在多层速度模型的基础上，使用二阶迎风格式离散对流项；Wang 等[60]将二阶TVD 和五阶WENO 格式[10]与Kataoka-Tsutahara多层速度模型结合使用；许爱国等[39]则使用了NND 格式[61]来处理对流项，并在一维和二维黎曼问题的计算中取得较为满意的结果。

使用隐式时间离散是传统CFD 方法中提高数值稳定性的常用方法，伴随而来的是需要迭代求解线型代数方程组，这往往使得计算量和实施难度显著增加。在FDLBM 中，Guo 和Zhao[62]使用了与经典LBM 类似的隐式时间处理办法，即类似于式（30）定义一个中间时刻的f¯a代入FDLBM 方程中，可将隐式方法转换为显式方法。Wang 等[60]沿用类似的思路，将隐式-显式Runger-Kutta 格式[63]引入FDLBM 并消除了隐式格式需要的迭代求解过程。

为了适应复杂几何构型和不规则形状网格的计算需求，Nannell 和Succi[64]、Benzi 等[65]将有限体积方法引入LBM，提出了FVLBM 方法。FVLBM 的基本思想是，将LBM 方程（式（104））对流场中任意一个控制体单元 Ω （边界为 ∂Ω ，此处 Ω不代表碰撞模型）进行体积分得到：

则式（123）可写为关于分布函数单元体平均量和单元面对流通量的方程。求解该方程的过程即与传统有限体积方法类似。Chen[66]和Peng 等[67]将FVLBM的理论和其在非均匀网格上的应用进行了完善。为了提高稳定性，Stiebler 等[68]使用迎风型格式重构单元面通量。Patil 和Lakshmisha[69]则将TVD 格式应用于单元面通量的重构。

随着计算流体力学有限元方法日趋成熟[70-71]，Lee 和Lin[72]、Shi 等[73]将有限元方法引入LBM，发展了 有 限 元LBM 方 法。近 年 来，MacMeccan 等[74]、Krüger 等[75]使用混合型有限元LBM 方法模拟了可变形颗粒流动并应用于生物流计算领域。由于主题和篇幅所限，此处不对有限元LBM 方法作进一步展开。有兴趣的读者可参阅有关文献了解相关细节。

6 总结与展望

LBM 多层速度模型起源于单层速度模型，在热流和可压缩流动应用需求下不断发展，经历了平衡态分布函数展开从二阶提高到四阶、离散速度模型从单层网格提高到2 层或者更多层网格、约束条件也逐步增多的过程。Hermite 多项式模型则提供了一个既理论又实用的判定框架：要想准确还原能量方程，平衡态分布函数必须展开到速度四阶量。Watari-Tsutahara预设的多层速度模型[24-25]与该结论殊途同归。Hermite 多项式模型也同时指出，离散速度模型事实上为相应阶数积分公式的积分点和权重，只需查表（或用程序包计算）找出这些积分点和权重，选出一组应用即可，而不是根据经验预设和优化。尽管Hermite 多项式模型给出了较为简洁和确定的形式，但是依照经验理论进行马赫展开或待定系数得到的其他多层速度模型，在特定范围和领域内仍具有一定的应用价值。

必须承认，相对于计算等温弱可压流动的经典单层速度模型而言，多层速度模型仍然是一种尚不成熟的模型，在很多方面仍然需要改进和完善。这主要在以下几个方面：

1）模型的误差、色散与耗散、稳定性分析。目前对单层速度模型的误差和稳定性分析已有不少工作，例如：Sterling 和Chen[76]对D2Q7（六边形模型）、D2Q9 和D3Q15 进行线性稳定性分析后得出 τ ＞0.5才能稳定的结论。Marie 等[77]对D3Q19 模型进行色散和耗散分析，并与低色散高阶差分格式进行了比较。Silva 等[78]和Bauer 等[79]对最常用的D3Q15、D3Q19和D3Q27 模型进行了截断误差分析，指出这三种模型都能在低马赫数下还原动量方程，但是动量输运项的高阶截断误差不同，这将导致在各向异性流动的计算中出现较大差别；在将平衡态分布函数展开式根据连续平衡态分布函数的二阶矩约束条件和D3Q19 速度模型进行系数修正后，能获得与D3Q27 模型相当的各向同性水平。

对多层速度模型而言，McNamara 等[80]对D3Q21模 型（D3Q15 加 上 (±2c,0,0)、 (0,±2c,0) 和 (0,0,±2c)这6 个离散点）进行了时间离散格式分析，指出使用Lax-Wendroff 时间格式将在高瑞利数下具有更好的稳定性。Wissocq 等[81]则对D2Q9 和D2V17 进行了模态和稳定性分析，指出D2V17 能准确解析线性等温Navier-Stokes 方程的3 个特征值模态，而D2Q9 则在这些模态的高波数上产生一定的误差。这一点与Hermite 多项式模型的结论是一致的，即只有使用七阶积分公式的积分点（即D2V17 模型）作为离散速度点才能准确还原动量方程；否则由于速度三阶量误差的存在而必须使用低马赫数假设。

值得注意的是，在Hermite 多项式模型框架下，经典D3Q15、D3Q19 和D3Q27 模型从积分精度角度来讲，并不存在差别，因为都具有五阶积分精度；从计算经济性原则来讲，应该选择积分点最少的D3Q15 模型。然而Silva 等[78]和Bauer 等[79]的工作提示我们，在选择离散模型时还需要考虑各向同性、截断误差等更多方面的因素，即计算最经济的模型不一定是最优的计算结果。Sieber 等[82]将Hermite 多项式模型与D2Q9 模型、Chen 等[23]的多层速度模型进行了线性稳定性分析对比，发现对等温弱可压流动而言，将平衡态分布函数展开到三阶Hermite 多项式级数，或使用D2V17、D2V37 模型都能显著提高稳定性；对于可压缩热流而言，使用四阶Hermite 展开的f(0)与D2V37 模型，稳定性都优于Chen 等[23]提出的多层速度模型。该结论在Hermite 多项式模型的理论框架下是易于被推断的。然而，对于完全还原了能量方程、且离散速度点数量最少的D2V37、D3V103 模型[47]而言，与同阶积分精度、但具有更多离散速度点的模型横向对比，例如D3V107 模型，是否也存在各项同性、稳定性、色散和耗散差异？这一方面需要在后续工作中展开详尽地理论分析；另一方面也需要大量的数值试验，例如方管Poiseuille 流动、旋转管道流、强可压缩流动、大温差热流等实际流动计算，来验证这些多层速度模型之间的性质差异。

2）边界条件。LBM 单层速度模型在经过多年发展后，其边界条件处理方法已经日趋完善，有关工作可谓汗牛充栋[33,36,83]，对于壁面反弹边界条件[56,84]、周期边界条件[85]、适用于流动出入口的无反射边界条件[86-87]以及其他类型的边界条件等都已有充分的研究工作，可满足绝大多数计算工况的需求。然而，当使用多层速度模型时，一方面由于离散速度点跨越多层网格，使得边界附近的内部结点与边界结点区分变得模糊；另一方面平衡态分布函数的形式也变得更为复杂，如何恰当处理边界条件成为了一个难点，相关的工作也屈指可数[83]。Malaspinas 等提出[88]，将边界节点的分布函数离散点按内部和边界分为已知量和未知量，将离散分布函数各阶矩的约束条件构成方程组，通过求解方程组构造一种“通用”的边界条件处理方法。他们在D2Q9 和D3Q19 模型中进行了测试，并指出该方法可适用于多层速度模型的边界条件（但没有后续验证）。Meng 和Zhang[89]提出了适用于多层速度模型的扩散-反弹边界条件格式，并应用到D2V16、D2V17、D2V37 和D3V121[45]这四种模型，对等温流动和热流进行了测试计算。Lee 等[90]将Hecht 和Harting 针对D3Q19 的非平衡态壁面反弹边界条件[91]，推广到了用多层速度模型计算等温弱可压流动的情况，并用D2V17 模型进行了验算。Klass等[92]进一步延续了Lee 等的工作，并将其应用到了弱可压热流中，使用D2V17 和D2V37 模型进行了验证，计算结果比Meng 和Zhang 的扩散-反弹边界条件表现更优。总体来看，针对多层速度模型的边界条件研究工作还处于起步阶段，且大部分局限于弱可压热流和Dirichlet 边界类型；对于压缩性较强的跨声速、超声速流动，以及流动出入口涉及的无反射边界条件，尚无相关工作涉足。将单层速度模型中的各类边界条件处理方法扩展到多层速度模型，并在各类流动中广泛验证测试，仍是今后需要较多投入的方向。

3）高性能算法。LBM 最大优势是计算速度和高度并行特性，然而它也有一个众所周知的缺点：由于需要存储数量众多的离散分布函数，对计算机内存的使用量比传统CFD 方法更多，因此有不少工作聚焦于如何改进算法，减少内存消耗并提高计算效率[93-95]。另外，正如上一节所述，经典的LBM（相对于FDLBM 和FVLBM 及其他混合方法而言）一般使用均匀网格，当涉及到边界层计算时，将LBM 与自适应局部加密网格（AMR）结合[96-98]是更加经济有效的方案。这些算法与目前流行的GPU 高性能计算相结合，能发挥LBM 的最大计算潜力[99-101]。然而，目前这些高性能算法都是集中应用在单层速度模型中。对于多层速度模型而言，特别是三维情况，准确模拟可压缩热流的最经济模型是D3V103，但其分布函数离散点的数量已经是D3Q27 的4 倍。这一方面使其内存占用问题更加突出；另一方面，在并行化和局部自适应加密网格时，不同块之间的界面数据交互量也更大，需要相当谨慎地处理。然而这些往往是工程实际应用中决定算法效率的制约因素。发展适用于多层速度模型的高性能算法，包括内存节约算法、高效率通信和AMR 方法、CPU+GPU 异构高效算法，并在各类复杂几何外形、复杂流动中广泛测试，应引起业内学者的广泛关注。

总体来说，LBM 模型，特别是多层速度模型，仍然需要诸多补充和完善才能成为一种可靠、高效的流体力学研究手段和应用技术。正如1998 年Chen 和Doolen[2]在文章结尾中提到，LBM 多相流和复杂反应系统模型主要集中于等温弱可压流问题，适应于可压缩热流的LBM 模型仍待开发。20 余年后的今天，这些方面虽然取得了一些进步，但是离可靠性要求还有不少差距。我们期望多层速度模型能够百花齐放，特别是具有较完备数学理论框架的Hermite 多项式模型，能在这些方面继续发展壮大并做出应有的贡献。

附录A