基于DSP的柴油机振动信号小波降噪实时性研究

应 铭，冯国胜 ，贾素梅 ，霍肖楠 ，马春庭

(1. 北京理工大学 机械与车辆学院，北京 100081；2. 石家庄铁道大学 机械工程学院，河北 石家庄 050043； 3. 石家庄铁道大学 河北省工程机械动力与传动控制重点实验室，河北 石家庄 050043； 4. 河北军涛科技有限公司，河北 石家庄 050000)

柴油机已广泛应用于工业、农业、交通运输业和国防建设事业，是为多种机械提供动力的核心构件．柴油机故障会造成经济损失和人员伤亡．传统故障诊断的过程一般为：采集数据、分析数据和检出故障．在实际应用中，分析数据的速度往往要慢于采集数据的速度．这导致了故障的发现存在一定滞后性，发动机在一定时间内带故障继续运行，且两次采集的数据之间存在间断，可能导致间歇性故障漏诊断．这种现象在需要高采样频率的诊断信号中尤为显著，采样频率越高，短时间内获得的数据量就越大，处理大量数据所需时间也越多．

柴油机缸盖振动信号包含丰富的状态信息[1-2]，且传感器安装容易、成本较低，是理想的监测信号来源．但柴油机缸盖振动的激励源较多，要获取其完整频谱，需在较高采样频率下采集[3-4]，且振动信号包含燃烧噪声、活塞敲击噪声、进/排气门落座噪声、喷油泵噪声和正时齿轮噪声等多种噪声[5]．噪声不仅会干扰缸内压力、燃烧状态等工作参数的提取[6-7]，也会影响故障的检出率[8]．

经验模态分解(EMD)和小波变换(WT)是处理非平稳信号的常用手段[9-10]．EMD缺乏严格的数学理论模型支持，各个固有模态函数(IMF)分量不正交，信号重构时易产生混叠模态[11]，且其在运算时间上不稳定，不适合在嵌入式平台上移植．小波变换已被广泛运用于分析具有瞬态、非稳态或时变特性的信号[11-12]．但传统小波变换实现算法的运算速度较慢，难以满足高采样频率下的实时降噪需求．提升小波也称为第二代小波，同时具有实时性强和原位运算的优点[13-14]，但以往对小波降噪实时性的评价依赖统计小波变换运算过程中乘法和加法的次数[15]，并未考虑工程应用中算法运行载体—数字信号处理器(DSP)的占用时间．影响了对小波降噪实时性评价的

准确性，使得评价结果不能真实反映工程应用情况．且小波降噪参数大多仅根据降噪效果进行选择，并未考虑实时性的影响．目前，从实时性角度对小波进行的研究较少，有必要构造高实时性的小波降噪系统进而提高检测仪器的诊断实时性．

笔者以工程应用中的算法载体DSP为研究对象，分析了小波算法的实时性评价方法及考虑实时性的小波参数优选方法，以期解决工程实践中实时小波降噪系统的构建问题．

1 小波变换概述

对一能量有限信号[16]f(t)，满足

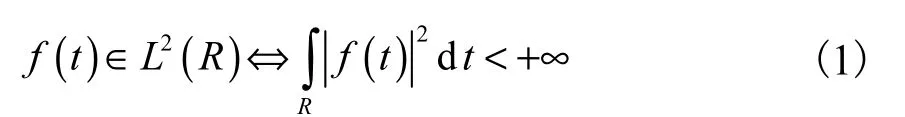
式中L2(R)为实数域中的平方可积空间．

记f(t)的傅里叶变换为Ψ(ω)，若Ψ(ω)满足容许性条件CΨ，即

则称Ψ(t)为一个基小波或母小波，将基小波Ψ(t )进行平移、伸缩可得到一个小波函数Ψa,b(t )，即

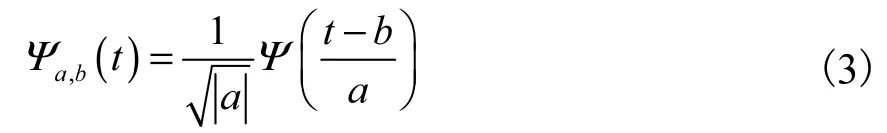
式中：a为尺度因子；b为平移因子．

则能量有限信号f(t)的连续小波变换(CWT)为

式中Ψ*为对Ψ的共轭运算．其逆变换定义为

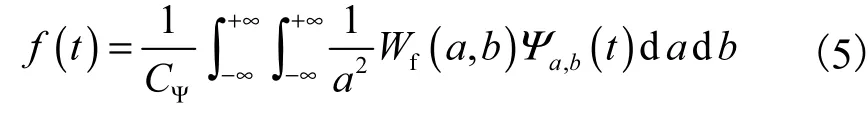
在实际应用中，所采集的信号都是离散化的，故需对连续小波进行离散化．对于小波函数(式(3))，假设a,b∈R，a＞0且a≠1，Ψ(t )满足容许性条件．将尺度因子a和平移因子b离散化，a以幂级数的形式离散化，b以均匀抽样的方式离散化．

离散化的小波函数为

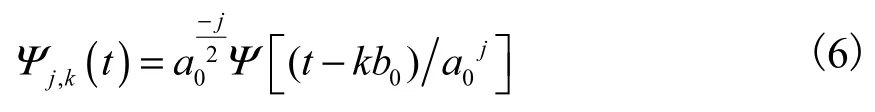
式中：j、k为整数；a0、b0为常数，且a0≠1．

则离散小波变换(DWT)定义为

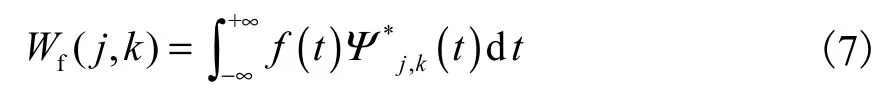
其逆变换定义为

式中c为与原始信号无关的常数．

2 小波变换指令周期模型

指令周期是指DSP取出并执行一条指令所需的时间，指令周期模型即算法执行总计所需的指令周期个数．小波变换包括取值、赋值、乘法和加法等指令，在DSP中这些指令耗时相等，则传统的忽略赋值和取值指令的统计方法不适合在DSP中使用．乘积累加运算(MAC)的定义为

式中：A、B和C为常数．

MAC包括取值、赋值、乘法和加法，基于硬件设计，DSP可在一个指令周期内完成一次MAC．

2.1 经典小波指令周期模型

经典小波的实现依赖于Mallat算法，该算法可分为延拓、卷积和下采样3个步骤[17]，有

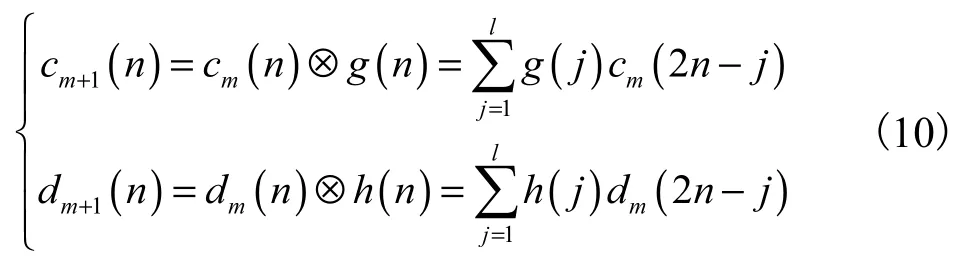
式中：n为小波变换序列点数；m为当前分解层数；cm和dm为第m层分解的近似系数和细节系数；g(j)和h(j)为低通和高通滤波器的第j个系数；l为滤波器长度．将式(10)改写为乘积累加形式，有

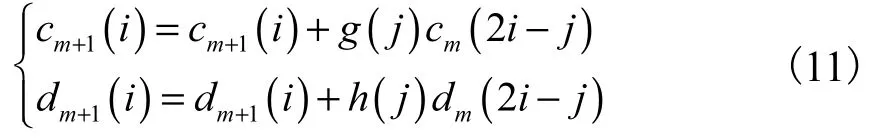
式中：i =1，2，3,…,n ；j=1,2,3,…,l．可知，使用Mallat算法对点数为n的序列进行小波变换需要(l·n)次MAC和(l2-l)次延拓赋值，故Mallat算法的指令周期模型为

2.2 提升小波指令周期模型

提升小波也称第二代小波，其保留了经典小波多分辨率的特性，提升小波的构建经过奇偶分裂、预测和更新3个步骤[18]，有

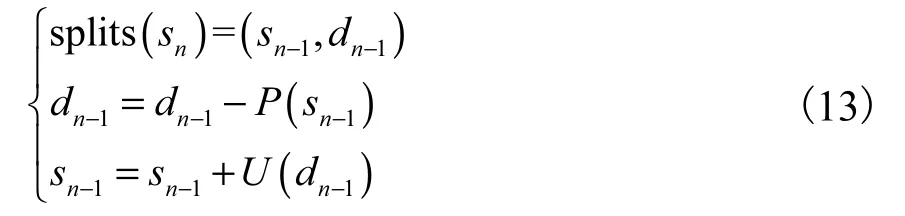
式中：splits(sn)表示将序列sn按位置奇偶分裂；dn-1为奇数序列；sn-1为偶数序列；P为预测算子；U为更新算子．将式(13)改写为乘积累加形式，有

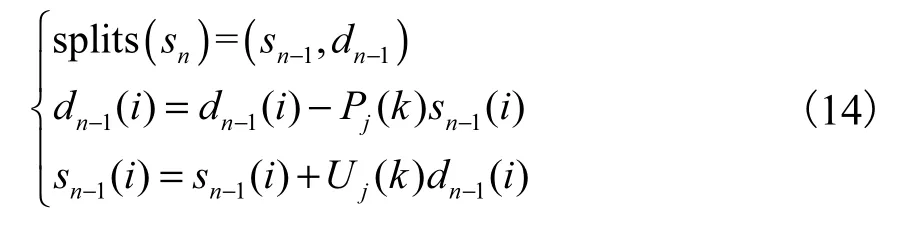
式中：i=1，2，3…，n/2；j=1，2，3…，p；k=1，2，3…，lj；Pj(k)和Uj(k)分别为预测、更新算子第j次预测、更新步骤的第k个系数；p为预测、更新步骤的次数；lj为预测、更新算子第j次预测、更新步骤的长度．可知，一次提升小波变换需要次的MAC．

2.2.1 原位运算提升小波指令周期模型

“搭脚手架”实践其实并不难，我们大部分家长只是没有这个意识。下面是几个我自己在教学中总结出来的主要核心点。

提升小波可以实现原位运算，原位运算是指仅使用原序列空间，不需其他辅助空间的运算过程．但原位运算可能导致运算速度降低．文献[19]给出了奇偶分裂的原位运算方法，该方法所需的最小指令周期为3n2/16．

则原位运算提升小波指令周期模型为

2.2.2 非原位运算提升小波指令周期模型

奇偶分裂非原位运算的快速实现方法是将原始信号的奇数、偶数序号放入辅助数组的前半部分和后半部分，非原位运算的奇偶分裂需要n条赋值指令．

则非原位运算提升小波指令周期模型为

2.3 多层小波变换指令周期模型

对于分解层数为q的多层小波变换，可近似认为每层变换的序列点数为上一层的一半，则q层小波变换的指令周期模型为

式中：q为小波分解总层数；T(21-k·n)为第k层分解时所用小波算法的指令周期模型．

将式(12)、(15)和(16)代入式(17)计算，可知，Mallat算法和非原位运算提升小波所需的指令周期与小波变换序列点数呈正相关；原位运算提升小波所需的指令周期与小波变换序列点数呈二次相关．在相同预测、更新算子下，当小波变换序列点数超过8时，原位运算提升小波所需的运算时间将超过非原位运算提升小波；若记为预测、更新算子的长度，则Mallat算法与非原位运算提升小波所需运算时间的长短取决于该小波基函数对应的滤波器与预测、更新算子的长度．

对于多层小波变换，Mallat算法和非原位运算提升小波第k层分解所需的指令周期为第(k-1)层的一半；原位运算提升小波第k层分解所需的指令周期为第(k-1)层的1/4．

3 柴油机缸盖振动信号的小波降噪

小波变换的分解层数、预测、更新算子和滤波器的长度对小波实时性有显著影响．笔者以CA4DF3-13E3型柴油机为对象研究柴油机实时监测系统中小波降噪的合适参数，表1为柴油机的主要技术参数．

表1 发动机主要技术参数 Tab.1 Engine specifications

图1为CA4DF3-13E3型柴油机缸盖振动加速度的测点位置．试验设置采样频率为25kHz，分别采集800、1000、1200、1400、1600、1800、2000和2300r/min空载工况下第1缸缸盖振动加速度，每次 采集5000点数据．图2为低、中和高速3种典型工况下缸盖振动的功率谱密度．

图1 测点位置Fig.1 Location of measuring point

小波分解层数会影响降噪效果与实时性．分解层数过多，会导致原始信号被过度降噪失去原有特征，且实时性较差；分解层数过少，会导致原始信号降噪不完全．柴油机缸盖振动信号能量主要集中在频段0～1.6kHz(图2)．一次小波分解会将原始信号等分为高、低两个频带，图3为根据功率谱密度计算 不同层数小波分解的低频能量相对总能量的占比．

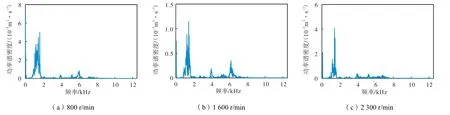
图2 功率谱密度Fig.2 Power spectral density

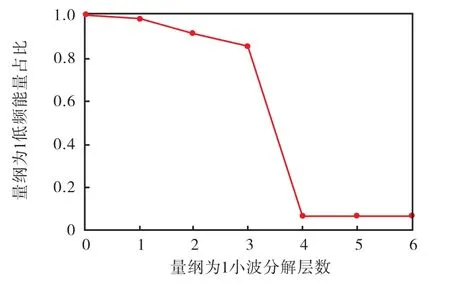
图3 频带能量比例Fig.3 Band energy ratio

低频能量占比在第4层小波分解时出现显著下降，说明振动信号的主体特征在第4层小波分解时被划归到需降噪的高频部分．为保留信号主要特征，防止过度降噪，选择小波分解层数为3层．

小波基函数决定了Mallat算法中滤波器的长度和提升小波中的预测、更新算子，合适的小波基函数应同时具有较好的降噪效果和较强的实时性．为对降噪效果进行评价，通常将信噪比作为评价降噪效果的主要指标，但信噪比的计算需以不含噪信号作为参考，而在缸盖振动测量过程中，不含噪信号是不可测的．因而可通过组合均方根误差和平滑度给出一种小波降噪复合评价指标[20]，均方根误差与平滑度呈负相关，在组合的过程中会出现一个极值，该极值表示去噪后信号保留的细节信息和逼近信息达到了最 佳比例，其对应的为寻找的最优小波基函数为

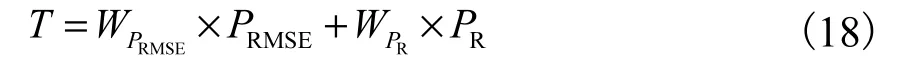
式中：PRMSE为归一化后的均方根误差；PR为归一化后的平滑度；WPRMSE和为通过变异系数定权法所确定的权值．T最小时表示降噪效果最优．变异系数定权法是指在评价指标体系中数值差异越大的指标，即越难实现的指标，因而要赋以更大的权值．权值的计算方法为

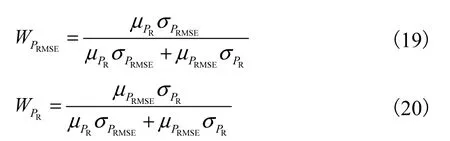
式中：σ和μ分别为求标准差操作与均值操作．

式(18)的评价指标仅对降噪效果进行评价，为综合评价小波基函数的降噪时间和降噪效果，利用变异系数定权法将降噪效果和降噪时间线性组合，进一步提出综合评价指标S，有

式中：PT和Pt为多工况下归一化的平均降噪效果和平均降噪时间；和为通过变异系数定权法确定的权值．由于小波基函数的降噪时间一般与降噪效果呈负相关，且两者均为最小时最优，故S存在极小值，该极值表示降噪效果和降噪时间达到了最佳比例，此时该小波基函数为综合最优．

若函数仅在有限的定义域范围内存在非零函数值，在该区间外的函数值全为0，称该函数在这个区间上紧支，具有该性质的小波称为紧支撑小波，只有紧支撑小波才可用于离散小波变换．正交小波具有去除各子带数据相关性的特性，且计算量相对非正交小波要小，更适合用于实时降噪．笔者筛选出工程应用中针对振动信号应用较为广泛的紧支撑正交小波基函数db1～db25、sym1～sym25、coif1～coif5与紧支撑双正交小波基函数bior1.1～bior6.8，图4为各小波基函数在多种工况下的平均降噪时间及平均降噪效果．

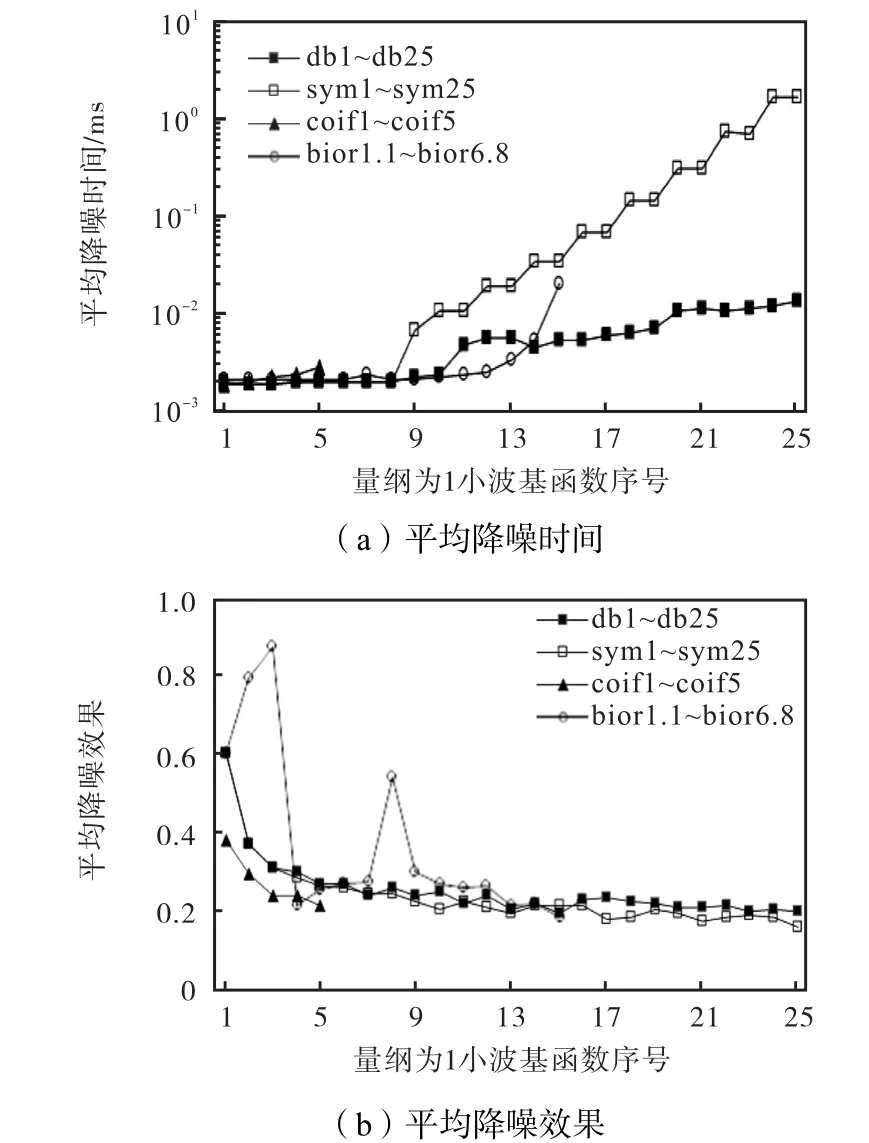
图4 不同小波基函数降噪时间与降噪效果Fig.4 Noise reduction time and noise reduction effect of different wavelet basis

图5为进一步计算得到小波基函数的综合评价指标S．小波基函数序号从左至右分别为db1～ db25、sym1～sym25、bior1.1～bior6.8和coif1～coif5．可知，S存在4处较小点，其中最小值出现在2号处，坐标为(53，0.029061)，其对应的小波基函数为bior2.2，故bior2.2为综合最优小波基函数．

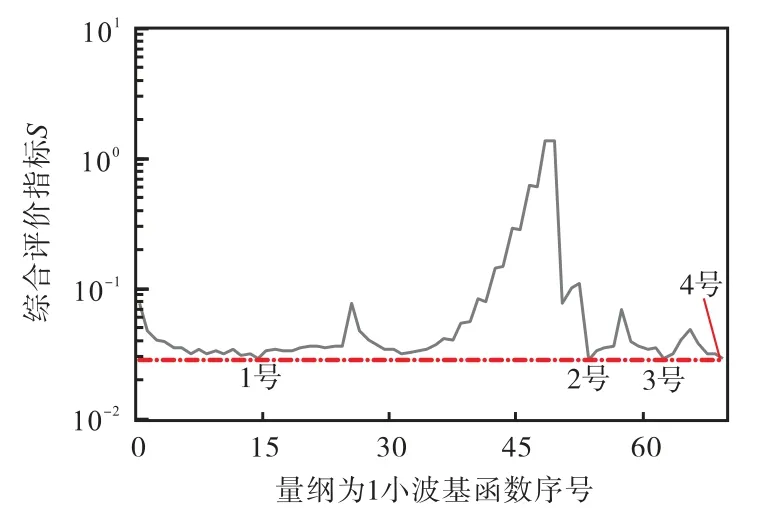
图5 不同小波基函数综合评价指标Fig.5 Comprehensive evaluation index of different wavelet basis

4 基于DSP的监测系统实时性试验

试验选用可提供150MIPS指令速度的32位数字信号处理器TMS320C28x作为信号处理的核心芯片．为了实时评价所选参数，定义实时性特征δ为

式中：ts为采样时间；ta为分析时间；δ越小，实时性越强，δ≤1时可实现实时处理．

试验设置采样频率为25kHz，选用3层小波分解和bior2.2小波基函数．通过算法相应的指令周期模型计算其实时性特征，并在TMS320C28x上通过试验获取了不同算法在不同采样点数下的实时性特征，如图6所示．

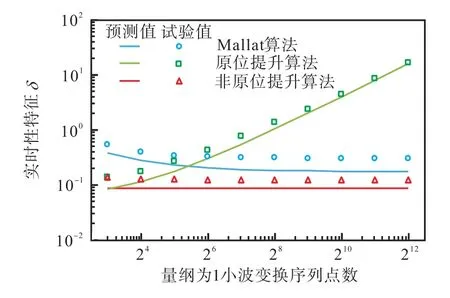
图6 不同小波实现算法的实时性对比Fig.6 Real-time comparison of different wavelet algorithms

可知，试验结果与建立的小波变换指令周期模型吻合较好．但试验所得的实时性特征值略高于指令周期模型预测值，这是由于在函数运行过程中存在临时变量建立、循环变量累加等原因，导致实时性变差．

不同的小波变换序列点数对实时性有较大影响．为获得较好的降噪效果，需合理确定小波变换序列点数，小波变换序列点数的统计特征应与被测信号整体的统计特征基本一致．柴油机缸盖振动信号随曲轴旋转呈周期性变化，一个完整旋转周期能较好地代表柴油机短时间内的运行状态．取怠速时曲轴旋转一周时间(0.075s)，则小波变换序列点数应大于0.075×25000＝1875．此时使用非原位运算提升小波的实时性最优且满足δ≤1，可以满足在25kHz采样频率下的实时降噪需求．

5 结 论

(1) 原位运算提升小波运行所需的时间随变换序列增加呈二次增长关系，非原位运算提升小波和Mallat算法运行所需时间随变换序列增加呈线性增长关系；当序列点数超过8时，非原位运算提升小波的实时性将优于原位运算提升小波．

(2) 指令周期模型能较好地拟合DSP中小波算法的实时性，但根据模型计算所得的实时性会稍强于实际运行时的实时性．

(3) 提供150MIPS指令速度时，选用3层小波分解和bior2.2小波基函数，小波实现算法选用非原位运算提升小波快于Mallat算法和原位运算提升小波，且使用非原位运算提升小波可满足25kHz采样频率下的实时降噪需求．