基于灰色马尔科夫模型的道路施工期交通量预测

2022-07-13周姜宇吕佳璐周慧娟李洋洁南通大学江苏南通226019

物流科技 2022年7期

毛霖，周姜宇，吕佳璐，周慧娟，李洋洁（南通大学，江苏南通 226019）

0 引言

道路施工对周边交通的影响较大，而其中交通量预测是道路建设项目可行性研究工作的重要组成部分，它不仅是分析建设项目的必要性和可行性的基础，同时也是确定道路建设项目技术等级、工程规模及经济评价的主要依据之一。

目前关于交通量预测和其他领域这方面的研究都已经取得一定的成果。潘丽等人用灰色马尔科夫模型预测上海铁路客通量，提高了精确度；宋晓震等人将灰色马尔科夫模型应用于我国煤炭消费量的预测中，降低了单一预测方法的波动性和随机性；崔毅等人用灰色马尔科夫模型预测青岛冷链物流的需求量，更具有实用性，为需求的预测提供了数据参考。

而在交通量的预测中，常用的预测方法为四阶段法、灰色预测模型法等。董冲磊等人采用四阶段法对交通量进行预测，但是该预测方法需要的数据量大、耗时长；邓志龙等人通过灰色系统预测短时交通流，但是不适用于随机波动性较大的交通流量。

针对以上的研究，本文对基于灰色系统预测和马尔科夫链预测的道路施工期交通量预测模型进行深入研究，以期为交通建设及管理部门实施不同施工阶段的交通组织设计提供决策支持。

1 灰色GM (1,1 )与马尔科夫预测模型

1.1 灰色GM (1,1 )预测模型

灰色GM 1,( )1 模型就是通过少量的、不具备完全性的信息或数据从而建立灰微分预测模型并做出预测，它的建模步骤如下所示：

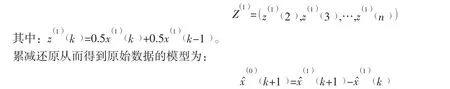
1.2 模型检验

1.3 马尔科夫转移矩阵

转移概率矩阵把概率矩阵用于马尔科夫链中相关的转移状态上，这时称这种概率矩阵为转移概率矩阵。其意义在于表现马尔科夫过程中事物由一种状态转变成另一状态的转移过程。若转移状态Р 用转移概率矩阵表示，则Р 即为转移概率矩阵，公式如下：

1.4 检验

相对误差检验：

2 应用实例

2.1 GM (1,1 )模型预测

建立施工路段的GM 1,( )1 模型，表1 为施工道路崇川路由西往东行驶车道从早7:00～9:30 每隔15 分钟的实地调查的交通量数据，运用Matlab 软件建立GM 1,( )1 模型。

表1 交通量数据表

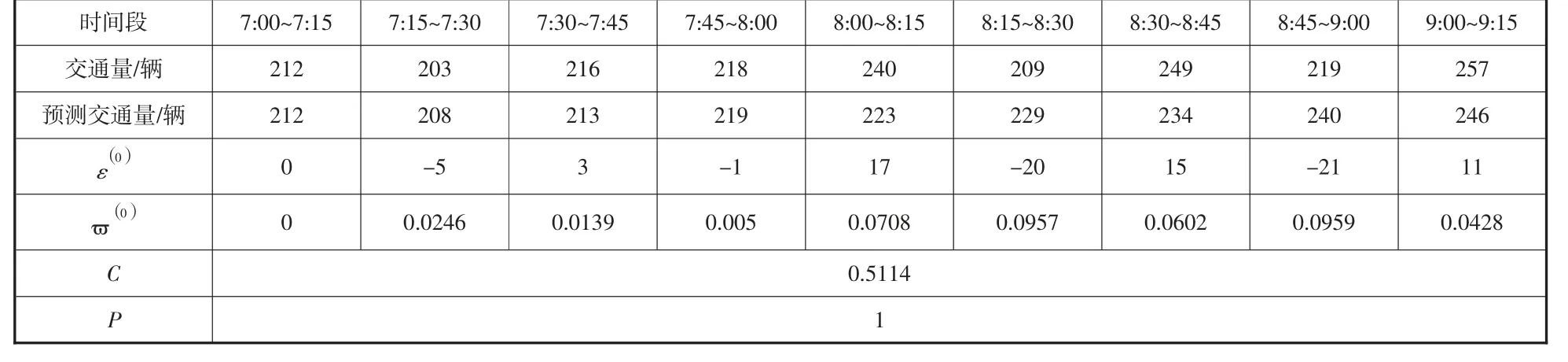
表2 各大指标对比

表3 灰色模型精度检验对照表

由预测出来的值对比发现，可知预测精度都属于比较好的状态，具有可信度。为了得到更精准的预测值，还要进行细化。预测的9:15～9:30 的交通量为246 辆。

2.2 建立残差绝对值序列的GM (1,1 )模型

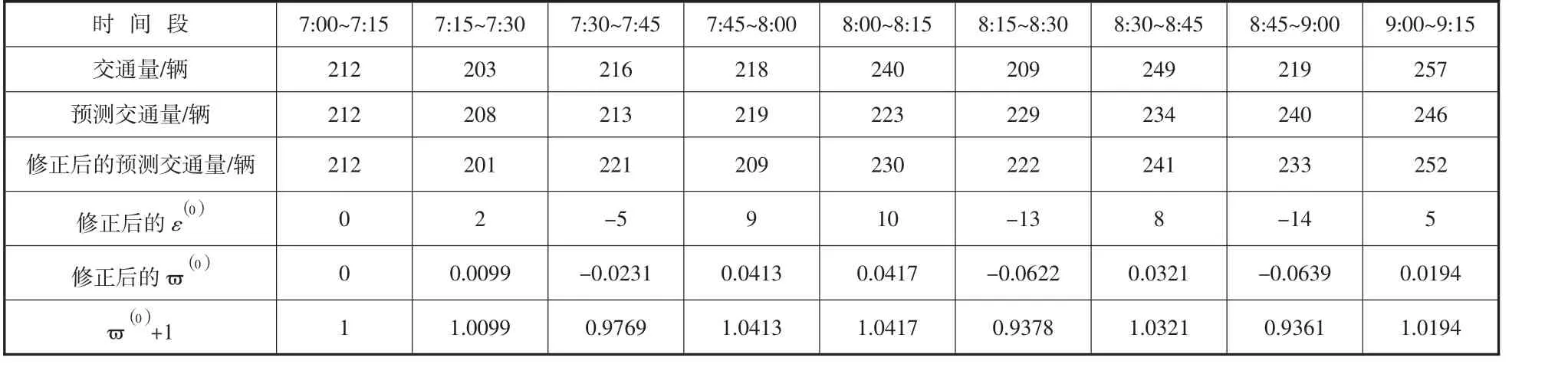
表4 传统GM (1,1 )与修正模型的预测值

表5 传统GM (1,1 )与修正模型精度对比

2.3 灰色马尔科夫优化

表6 相对误差和状态区间

2.4 构建状态转移矩阵

根据各时间段所在状态区间，由状态E转移到E出现的次数除以E的次数，得到相应的状态转移矩阵：

2.5 计算预测值

由状态转移矩阵及各时间段所处状态，可以求出崇川路9:15～9:30 交通量的马尔科夫预测值。选取与9:15～9:30 相隔时间最近的9:00～9:15, 8:45～9:00, 8:30～8:45 的实际交通量，分别对应1,2,3 步转移，同时，加入9:00～9:15, 8:45～9:00, 8:30～8:45 的初始状态，组成新的状态转移矩阵，计算各列向量之和，计算所得数值最大者即为9:15～9:30 对应的状态，如表7 所示。