高斯投影正反算与软件数据对比分析

雷云峰

摘 要：为了更好的利用国家坐标系和城市坐标系控制点成果，需要进行城市坐标系与国家坐标系之间的坐标换算，高斯投影正反算公式能很好解决不同投影带之间的坐标换算问题。通过一些数据对程序进行检验，结果能够实现正反算的互相转换，并且能够分别进行单点正反算和批量正反算。程序能够实现不同椭球的大地坐标和高斯平面坐标之间的相互转换。具有标准和非标准分带的转换功能。也通过与南方GPS数据处理软件中的坐标转换计算结果对比，结果精度达到要求。

关键词：高斯投影正反算;MFC框架;坐标转换

1、引言

高斯投影是正形投影的一种，具有投影长度比与方向无关，投影前后角度不变等优点，广泛应用于各种工程项目中。城市坐标系的中央子午线与国家坐标系相邻投影带的中央子午线存在一个差值，为了更好的利用国家坐标系和城市坐标系控制点成果，需要进行城市坐标系与国家坐标系之间的坐标换算，高斯投影正反算公式能很好解决不同投影带之间的坐标换算问题。

2、高斯投影正反算原理

2.1、高斯投影正算原理

高斯正算：由椭球面上的大地坐标求定高斯平面上相对应的平面坐标。正算原理中，对于子午线弧长的求法比较重要。

其中，X为子午线弧长;N为卯酉圈曲率半径;B为纬度（ 弧度制）;L为经差.

2.2、高斯投影反算原理

高斯反算是利用大地地理坐标系坐标（X，Y）来求其对应椭球坐标系（B，L）。

3、高斯投影正反算程序设计

3.1、MFC程序框架的建立及计算流程

在Visual C++程序中使用控件工具栏向对话框模板添加静态控件、编辑框控件和按钮控件，调整各个控件的大小和位置，设置各个控件的属性值，添加各项参数等设置。

3.2、MFC程序高斯正反算代码

（1）高斯正算代码

（2）高斯反算代码

3.3、MFC程序高斯正反算软件

4、高斯投影正反算数据成果比较

4.1、不同椭球下正反算结果比较

中央子午线：120°选择分带：3°

4.2、不同分带下所有数据结果比较

中央子午线：120°椭球：克拉索夫斯基椭球

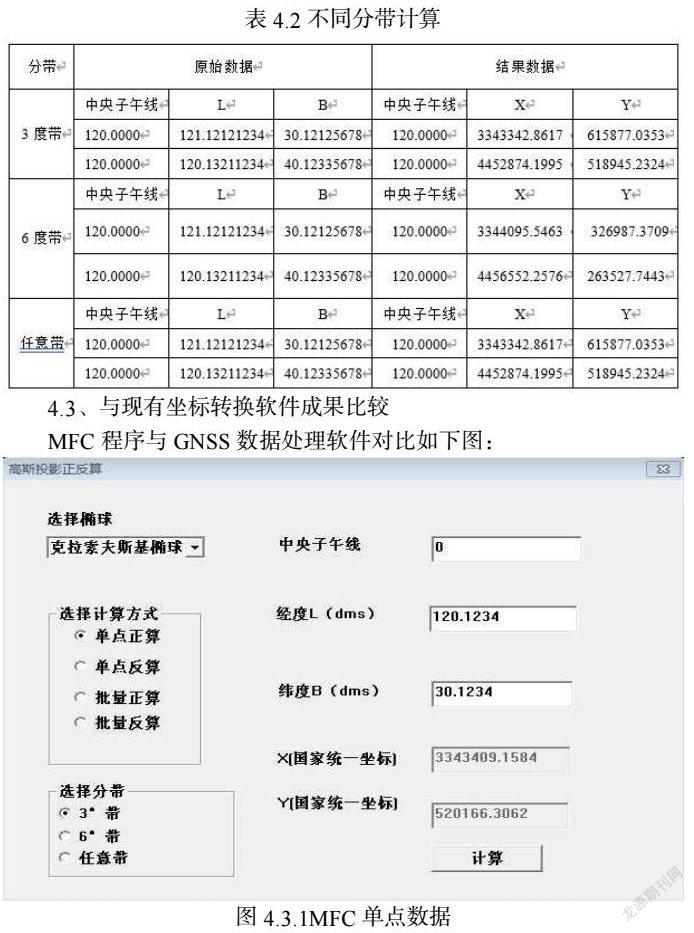
4.3、与现有坐标转换软件成果比较

MFC程序與GNSS数据处理软件对比如下图：

通过以上数据成果的比较可以看出本程序精度达到毫米后一位，通过与GNSS数据处理软件相比较得知，本程序达到精度要求。

5、结论

本文对于高斯投影正反算的算法，提到了直接应用与应用迭代法，可以看出应用迭代方法整个过程简洁、实用，精度上满足要求，迭代次数较少，运行速度较快，所以在高斯投影正反算中应用迭代的算法是很方便的。

MFC框架的构建是程序实现与否的重要环节，该框架是一个编写高效、更专业的工具，借助MFC应用程序框架可以更加方便地编写高斯投影正反算程序，在程序的编写过程中，借助建立好的MFC框架，使得整个程序更有条理性，更加方便地进行编写程序以及程序的调试。在程序的验证阶段，我随机选取了若干坐标进行了高斯正算，在正算完成后，又利用了正算结果进行了反算，通过验证发现高斯正算、反算结果一致，从而证明了高斯投影正反算程序的正确性与可靠性。

参考文献：

[1]车忠志，孙雪雁.MFC应用程序基本框架分析[J].农业网络信息，2010（09）：145-147

[2]陈正耀.高斯投影的计算与应用[J].北方交通，2013（04）：33-36