基于分形统计测度的动量组合投资策略优化研究
2022-07-12燕汝贞张菁洋
吴 栩,王 坤,燕汝贞,张菁洋
(成都理工大学 a.商学院;b.管理科学与工程博士后流动站,四川 成都 610059)
一、引 言
2022年,中国A股市场投资者突破2亿,市场机构化程度稳步提升,股票和基金投资已经成为不少家庭资产配置的重要组成部分。与此同时,伴随股票市场的不断发展和股票投资的蓬勃兴起,未来更多的投资者加入到股票和基金投资当中已是大势所趋。在A股市场开户数持续攀升和基金市场不断扩容的背景下,作为影响投资业绩的关键因素,投资策略受到了机构投资者和个人投资者的广泛关注。因此,研究投资策略自然意义重大。在研究投资策略时,尤其应该注重研究动量策略。动量策略是一种基于动量效应的趋势投资策略,通过做多前期表现好的资产、做空前期表现差的资产以获得超额收益,其存在性和有效性已在多个时期、不同国家和地区的资本市场及诸多资产类别中得到证实[1-5]。也正因如此,动量策略成为实务界最常用的投资策略,具有广阔的应用前景。中国股票市场起步晚、信息源单一、信息透明度低等诸多因素致使市场效率不高,这有利于动量策略发挥优势,研究发现中国大多数个人投资者和开放式基金皆采用动量投资策略[6-7]。可见,在众多投资策略中,研究动量策略尤其重要。
研究动量策略时,不应忽视权重分配方法。因为作为资产配置的重要内容,权重分配方法能够影响投资业绩[8-9]。然而,动量策略及其优化研究鲜少关注权重分配方法。传统动量策略采用累计超额收益率作为排序指标,且对赢者和输者组合进行简单的等权重处理[1]。Rachev等采用夏普比率、索提诺比率等多种风险调整后的收益率作为排序指标构建了风险调整动量策略,发现风险调整动量策略较传统动量策略能够获得更高更稳健的收益[10]。随后,Choi等相继采用在险价值、条件在险价值等作为排序指标构建风险调整动量策略,发现风险调整动量策略在全球股市、商品市场等不同市场中业绩表现均优于传统动量策略[11]。陆蓉等借助改进的偏度指标将股票划分为彩票型股票和非彩票型股票,研究发现在非彩票型股票样本中动量策略能够获得更好的业绩表现[12]。邓学斌等将换手率引入动量策略,发现低换手率的股票表现出更明显的动量效应[13]。可见,现有研究对于动量策略的优化大都集中于排序指标的优化和特定股票类型的选择,鲜少关注赢者和输者组合的等权重处理方法。同时,针对权重分配等问题,Markowitz所提出的投资组合模型早就给出了启示,该模型能够帮助投资者通过给予不同资产以最优权重,实现同等风险下收益最大化或同等收益下风险最小化,得到了学术界和实务界的广泛认可和应用[14-15]。因此,研究基于投资组合模型的动量策略考虑了权重分配方法,有利于进一步分散组合风险,实现策略的进一步优化,具有明确的实践意义和重要的理论价值。
研究基于投资组合模型的动量策略时,还必须以股票收益率的分形特征为约束。因为只有以金融市场的实际特征为约束,才能保证研究结论的可靠性和可用性[16-17]。诸多证据表明,股票收益率普遍具有分形特征,其尾部更是服从幂律分布[18-19]。进一步研究还指出股票收益率的分形特征具有必然性,只有分形理论才能做到股票收益和风险的准确测度,依靠其他方法很难得出可靠的结论[20-21]。因此,研究基于投资组合模型的动量策略时,要想保证结论的可靠性和可用性,就必须以股票收益率的分形特征为约束。此外,自分形市场理论创立至今,尽管涌现了众多成果,如魏宇和黄登仕建立了基于多标度分形谱两个主要参数的市场风险测度指标[22];吴栩等建立了基于分形理论的分形期望和分形方差两个统计测度,用以代替传统期望和方差测度股票的收益和风险,并将其成功应用于投资组合模型,构建了分形投资组合模型,但这些成果并没有与投资策略形成有效衔接,亟待突破[23-24]。以股票收益率的分形特征为约束,研究基于投资组合模型的动量策略,恰好将分形市场理论与投资策略结合起来,促进了分形市场和投资策略的衔接,扩展了现有研究成果,具有重要的理论价值。
综上所述,尽管现有研究对于动量策略进行了卓有成效的改进,但鲜少考虑权重分配方法和股票收益率的分形特征。基于此,本文以股票收益率的分形特征为约束,将投资组合模型纳入动量策略的研究框架。首先,借助多重分形去趋势波动分析法检验出股票收益率具有分形特征;其次,借助分形统计测度构建了分形收益风险比,并以此为排序指标构建了分形风险调整动量策略;再次,在分形风险调整动量策略的基础上,构建了带约束条件的分形投资组合模型,并利用该模型给赢者和输者组合分配最优权重以完成分形动量组合投资策略(FMP策略)的构建;最后,实证结果表明FMP策略的业绩表现明显优于风险调整动量策略、分形风险调整动量策略和传统动量策略,同时分形风险调整动量策略的业绩表现优于风险调整动量策略。
二、理论模型构建
(一)多重分形去趋势波动分析模型

(1)
步骤二:将时间序列划分为等长度且不重叠的子序列。由于时间序列一般都是无法整除的,为了不丢失尾部数据,从尾部进行重复划分并剔除多余部分。
步骤三:对每个子序列使用最小二乘法拟合趋势函数,拟合过程使用线性函数,拟合得到消除趋势的波动方程:
(2)
其中,pm(i)是采用最小二乘法拟合第m个子序列的线性趋势。
步骤四:计算q阶波动函数:
(3)
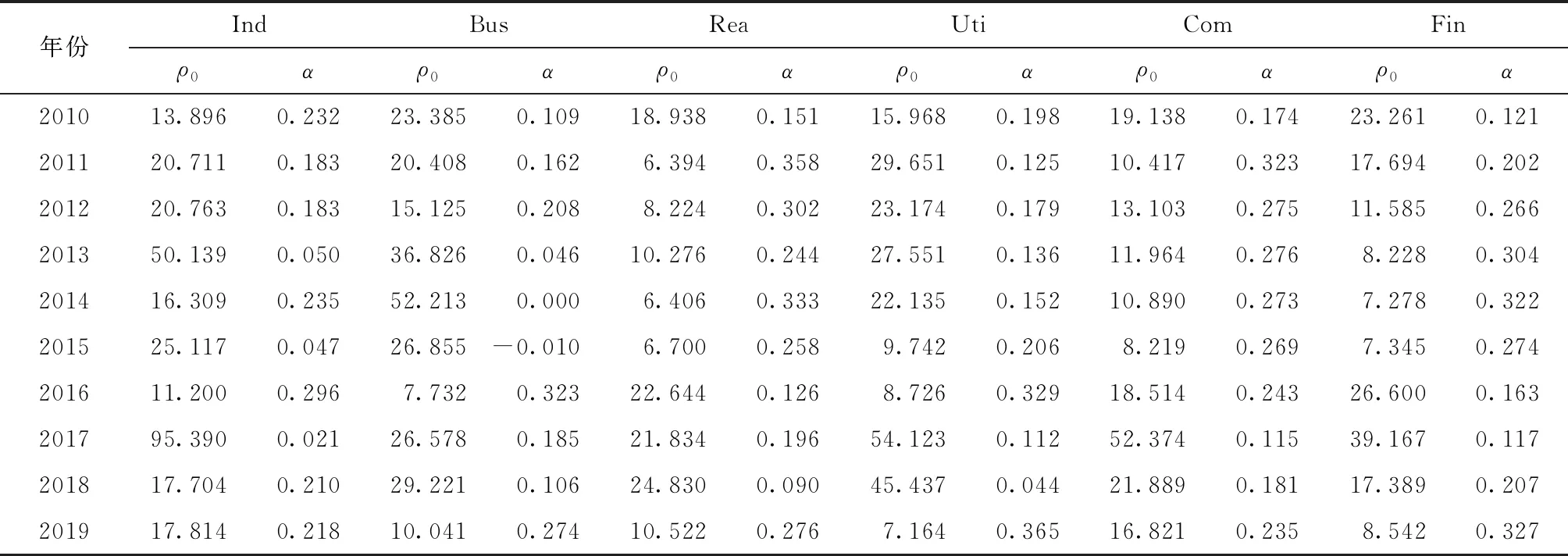
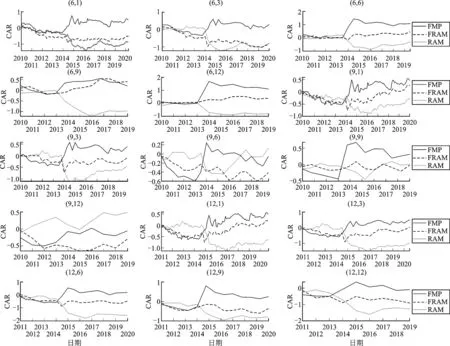
步骤五:计算q阶广义Hurst指数h(q)。若h(q)与q相关,则表明原时间序列具有多重分形特征。当0≤h(2)<0.5时,表明时间序列存在反持续性;当h(2)=0.5时,表明时间序列服从随机游走;当0.5 Δh=h(qmin)-h(qmax) (4) 根据MF-DFA模型,发现A股市场的股票收益率普遍具有多重分形特征,此时传统期望和方差难以准确测度股票的收益和风险[20-21]。在此基础上,采用吴栩等构建的分形期望和分形方差这两个分形统计测度作为量化股票收益和风险的测度指标[23]。假设存在一个随机变量X,密度函数为ρ(x),其中ρ0、α、c为大于0的常数,分形统计测度的构建方法见式(5): (5) 步骤一:根据反常积分的性质,随机变量X的传统期望E(X)和方差Var(X)可由式(6)表示。可知,当α<2时传统期望和方差将趋于无穷大,无法测度股票的收益和风险。 (6) 步骤二:当α<2时,随机变量X的期望可由式(7)表示。为简洁起见,不妨用数组〈(2-α)-1ρ0,2-α〉反映期望的变化过程,并将Ef(X)称为分形期望,计算为式(8)。同理,分形方差Varf(X)的计算为式(9)。 (7) Ef(X)=〈EX,eX〉=〈(2-α)-1ρ0,2-α〉 (8) (9) 步骤三:分形统计测度的计算法则可由式(10)和(11)表示,其中a、b、q为任意常数,X和Y表示密度函数为式(5)的随机变量。 (10) (11) 基于分形统计测度,首先构建了分形收益风险比,并将其作为排序指标构建了分形风险调整动量策略;其次,在分形风险调整动量策略的基础上,构建了带约束条件的分形投资组合模型,并利用该模型给赢者和输者组合分配最优权重,构建了分形动量组合投资策略(FMP策略)。 1.分形风险调整动量策略 (12) (13) 步骤二:对赢者和输者组合中的股票赋予相同权重,然后计算K期内赢者和输者组合的收益率。 (14) (15) 步骤三:计算K期内,动量策略的超额收益率。 (16) 2.分形投资组合模型 传统的动量策略,对赢者和输者组合进行等权重处理,但根据现代投资组合理论,通过对风险资产进行权重分配,可以在有效前沿上选择收益(风险)一定时,风险(收益)最小(大)的投资组合。因此,本文拟将投资组合模型纳入动量策略的研究框架,以求获得更好的业绩表现。同时考虑到股票收益率普遍具有分形特征,采用吴栩等构建的分形投资组合模型[23]。假设P为包含风险资产M和N的风险投资组合,F为无风险资产,模型的构建如式(17)~(19): (17) (18) (19) 3.FMP模型 基于分形风险调整动量策略和分形投资组合模型,下面利用分形投资组合模型对分形风险调整动量策略遴选的赢者和输者组合分配权重完成FMP模型的构建。同时值得注意的是,动量策略需要做多赢者组合和做空输者组合,即分形投资组合模型纳入动量策略时必须保证赢者组合所获得的权重为正和输者组合权重为负。因此,利用分形投资组合模型给赢者和输者组合分配权重时需要添加约束条件。具体过程为:将分形风险调整动量策略遴选的赢者和输者组合代入分形投资组合模型,同时附加约束条件,见式(20),计算得到赢者和输者组合对应的权重,最后利用式(21)计算得到FMP策略的超额收益率。其中,ωw表示赢者组合的权重,ωl表示输者组合的权重。 (20) (21) 上述理论分析表明FMP策略能够进一步提升动量策略的业绩表现,为检验理论分析结果的正确性,下面进行实证分析。本文数据采用上海证券交易所的六种行业指数的交易信息,即地产指数(Rea)、工业指数(Ind)、公用指数(Uti)、金融指数(Fin)、商业指数(Bus)、综合指数(Com),括号内为对应指数的简称,并以国债指数收益率为无风险收益率。样本期间为2010年1月至2020年10月,该期间包含了完整的市场行情,可以避免因时间过短而导致的实证结果对于现实的偏离。所有数据均来源于Wind数据库,数据基本特征如表1所示。 表1 六种行业指数收益率的描述性统计 表1给出了六种行业指数收益率序列的描述性统计。从表1可以看出,六种行业指数的收益率序列皆不服从正态分布,均具有明显的尖峰厚尾特征。图1为六种行业指数的收益率时序图,从图1可以看出,六种行业指数的收益率序列存在明显的波动聚集现象,印证了其收益率分布存在明显的尖峰厚尾特征。 图1 六种行业指数收益率时间序列图 利用MF-DFA模型对六种行业指数收益率序列的多重分形特征进行检验,结果如图2所示。其中,图2为阶数L=1和阶数L=2时,六种行业指数h(q)随q值变化的走势图。从图2可以看出,取L=2时广义Hurst指数不满足标度指数性质,所以应用L=1的MF-DFA模型进行分析。同时,从图2可以看出,h(q)不是常数,无论q值如何变化,h(q)总是随着q的改变而改变。除了金融指数,其他曲线在q∈[-2,2]区间内总是呈现平滑的非线性下降趋势,表示地产指数、工业指数、公用指数、商业指数、综合指数皆存在显著的多重分形特征。 图2 六种行业指数收益率的多重分形特征 表2给出了六种行业指数收益率的评价标度指数h(q)以及Δh的值。从表2可以看出,h(q)均大于0.5,说明收益率序列皆具有长记忆性;其次公用指数的Δh最大表明其多重分形程度最高,而金融指数的Δh最低表明其多重分形程度也是最低的。 表2 六种行业指数的h(q)以及Δh 表3 收益率序列密度函数的两个参数 为简洁起见,表3列出了2010—2019年每年的α、ρ0,同时表4给出了密度函数对应的拟合优度。从表4可以看出,60个回归方程拟合优度均高于0.9,表明收益率序列的密度函数确实为幂律分布。表3所示的密度函数的两个参数具有较高的可靠性,同时也佐证了将多重分形程度较低的金融指数假设为幂律分布的可靠性。 表4 密度函数的拟合优度 根据计算得到的密度函数α、ρ0的值,首先将其代入式(8)和(9)便可计算得到在时间段内股票的分形期望和分形方差,然后利用分形收益风险比作为排序指标构建分形风险调整动量策略,再次将分形期望和分形方差代入式(18)、(19)和(20)便不难得到数值形式的分形权重,最后将权重分配给分形风险调整动量策略遴选的赢者和输者组合完成FMP策略的构建。 为了检验FMP策略的有效性,对比分析了FMP策略、分形风险调整动量策略和风险调整动量策略的累计超额收益率(CAR),结果如图3所示。其中,排序期分别取6、9、12个月,持有期分别取1、3、6、9、12个月,共15个动量组合。之所以排序期没有取1、3个月是为了保证计算分形统计测度时所需样本量充足,确保回归结果的可靠性。图3中FRAM表示分形风险调整动量策略,RAM表示风险调整动量策略;(6,6)表示排序期为6个月,持有期为6个月的动量组合。根据图3,首先,对比分形风险调整动量策略和风险调整动量策略的业绩表现,发现73.33%的动量组合表现为分形风险调整动量策略优于风险调整动量策略;其次,对比FMP策略和分形风险调整动量策略的业绩表现,发现93.33%的动量组合表现为FMP策略优于分形风险调整动量策略;最后,对比三种策略的总体情况,发现80%的动量组合表现为FMP策略能够获得最佳业绩。因此,FMP策略无疑具有有效性。 图3 2010—2020年三种动量策略累计收益率对比 同时,为了进一步检验FMP策略的有效性,本文还比较了FMP策略和传统动量策略的业绩表现,结果如表5所示。表5给出了15个动量组合中FMP策略和传统动量策略的月平均超额收益率。从表5可以看出,在15个动量组合中,80%的动量组合表现为FMP策略优于传统动量策略;此外,FMP策略的月平均超额收益率的均值达到了0.31%,远高于传统动量策略。可见,FMP策略具有有效性。 表5 2010—2020年FMP和传统动量策略的月平均超额收益率 为检验上述结论是否具有稳健性,本文更换了样本,样本选择上海证券交易所六种行业指数,时间期间为2004年1月至2009年12月共6年时间,数据包括六种行业指数的交易数据。为验证FMP策略的稳健性,对比分析了FMP策略、分形风险调整动量策略和风险调整动量策略的累计超额收益率,结果如图4所示。从图4可以看出,在2004年1月至2009年12月期间,73.33%的动量组合表现为分形风险调整动量策略优于风险调整动量策略;15个动量组合全部表现为FMP策略优于分形风险调整动量策略;15个动量组合全部表现为FMP策略在3种策略中业绩最佳。同时,值得注意的是,与分形风险调整动量策略和风险调整动量策略不同,FMP策略总能获得正收益,这意味着,利用该策略能持续获得超额收益。因此,更换样本后,FMP策略依然具有有效性。 图4 2004—2009年三种动量策略累计收益率对比 同时,本文还比较了2004年1月至2009年12月期间FMP策略和传统动量策略的业绩表现,结果如表6所示。表6给出了15个动量组合中FMP策略和传统动量策略的月平均超额收益率。从表6可以看出,15个动量组合全部表现为FMP策略优于传统动量策略。此外,FMP策略的月平均超额收益率的均值达到了2.664%,依旧远高于传统动量策略。 表6 2004—2009年FMP和传统动量策略的月平均超额收益率 综上,分形风险调整动量策略表现优于风险调整动量策略,FMP策略表现优于分形风险调整动量策略、风险调整动量策略和传统动量策略。因此,实证结果表明,FMP策略不仅与理论部分相匹配,且具有有效性,有利于提升动量策略的业绩。 在A股市场开户数快速攀升和基金市场不断扩容的背景下,作为应用最为广泛的投资策略,动量策略受到了学术界和实务界的广泛关注,但鲜有学者考虑权重分配方法和股票收益率的分形特征。为此,本文以股票收益率的分形特征为约束将投资组合模型纳入动量策略的研究框架,构建了分形风险调整动量策略和分形动量组合投资策略(FMP策略),并利用回测检验对比分析了FMP策略、风险调整动量策略、分形风险调整动量策略和传统动量策略的业绩情况。研究结果表明:第一,A股市场的股票收益率普遍具有多重分形特征,其尾部近似服从幂律分布;第二,分形风险调整动量策略的业绩表现优于风险调整动量策略,说明分形统计测度优化了动量策略的排序指标;第三,FMP策略的业绩表现优于风险调整动量策略、分形风险调整动量策略和传统动量策略,说明优化权重分配方法能够进一步提升动量策略的业绩表现。因此,在股票收益率普遍具有分形特征,其尾部近似服从幂律分布的现实背景下,不仅可以通过优化排序指标,还可以通过优化权重分配方法提升动量策略的业绩表现。 综上,本文构建了一种以股票收益率的分形特征为约束基于投资组合模型的动量策略,促进了分形市场理论与投资实践的有效衔接,扩展了现有研究成果,具有一定的理论意义。此外,对于指导投资也具有重要的借鉴意义,我们可以通过优化排序指标和权重分配方法对动量策略进行双重优化,助力投资者提升业绩,顺应以人民为中心发展资本市场和提升投资者获得感等新时代要求。(二)分形统计测度的构建
(三)分形动量组合投资策略的构建
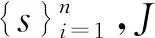




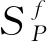
三、实证分析
(一)数据描述
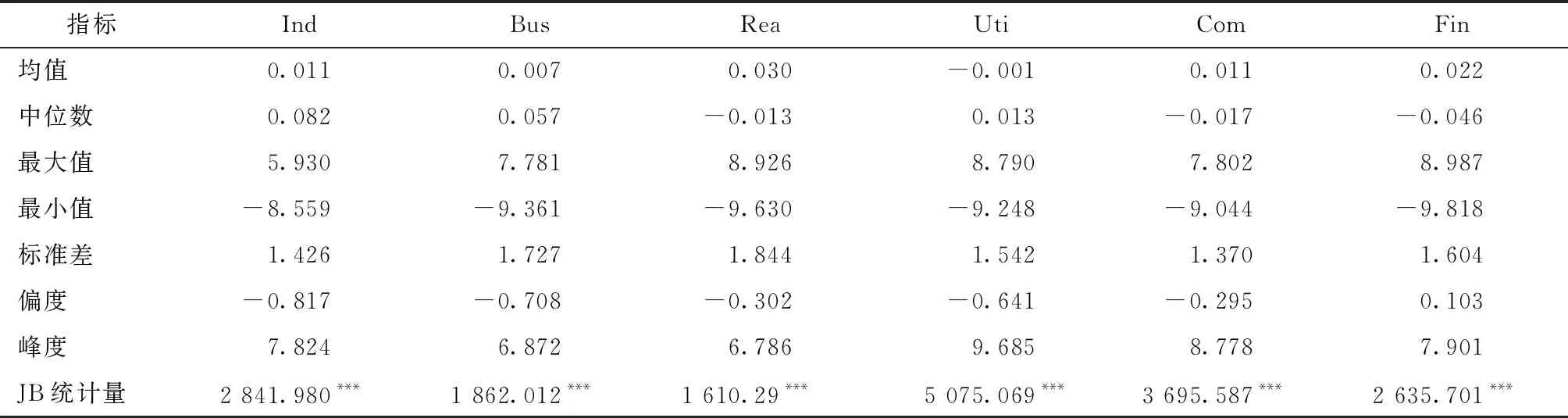

(二)股票收益率的非线性波动分析


(三)分形统计测度计算
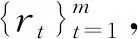

(四)FMP策略的有效性分析

(五)稳健性检验


四、结 论
