中国城市群经济韧性的地区差异、分布动态与空间收敛

杨桐彬,朱英明,姚启峰

(南京理工大学 a.经济管理学院;b.江苏产业集群决策咨询研究基地,江苏 南京 210094)

一、引 言

从均衡论视角看,区域经济韧性是指区域经济受到外部冲击后,恢复到原有发展水平的一种能力,或者能够吸收外部冲击,进而创造新的发展路径的能力。从演化论视角看,区域经济韧性是指区域能够不断调整自身经济、社会和政治结构以适应频繁发生的扰动冲击,最终实现区域经济长期发展的能力[1]。自2008年全球金融危机爆发以来,外部冲击对区域经济增长的影响一直是政府和学界关注的热点问题[2]。2020年突如其来的新冠肺炎疫情再次对全球经济造成严重影响[3]。纵观世界各国的发展进程,有的地区在经历经济危机、病毒传播、恐怖袭击等冲击后一蹶不振,有的地区却能克服各种自然和人为灾害带来的不利影响而持续发展,造成不同结果的本质原因便是区域经济韧性的差异[4]。

现有研究已然关注到行政区层面经济韧性的空间差异问题[5]。然而,经济韧性的空间差异同样可能体现在城市群层面。由于非核心城市通常面临高端人才引进困难、技术创新能力较弱、产业结构低端锁定等问题,严重制约经济韧性水平的提升,其与核心城市之间经济韧性的差距不断拉大。同时,城市群内部各城市之间人口等要素联系紧密,城市危机极易发生连锁效应与放大效应。此时,单个城市的应对能力显得尤为不足,迫切需要建立城市群联动机制,提升城市群风险抵抗能力。尤其是在中国努力构建以中心城市和城市群为主要空间载体的区域经济格局战略背景下,城市群空间网络关联的重要性日益显现,如何在城市网络体系中加强合作与互补,缩小城市间经济韧性差距,促进低水平城市尽快向高水平城市收敛,进而提升城市群整体的经济韧性,成为亟待解决的现实问题。

关于区域经济韧性的研究主要从概念定义、测算方法和影响因素等方面展开。从工程韧性到生态韧性,再到演化韧性,韧性思想实现了从追求稳定性均衡到探索适应性发展的跨越。当前主流观点是借助演化韧性思想,从动态适应性视角定义区域经济系统面对扰动冲击的抵抗能力。Simmie等认为韧性反映的区域经济适应过程是一种复杂的反馈、涌现与自组织并存的非线性动态过程,可以将区域经济演化过程分为重组、开发、维持和释放四个阶段[1]。Martin将区域经济韧性定义为区域经济系统通过对其产业、技术和制度等结构进行适应重组,减轻冲击造成的影响,维持系统继续发展或利用冲击实现系统更新的能力[6]。

在理论分析基础上,学者们开始尝试对区域经济韧性进行定量分析,而科学测算经济韧性成为定量研究的基础。现有方法主要包括指标体系法、关键变量法和函数分析法。Dinh等构建起包含人力、社会、自然、物质和金融资本存量、经济多样性以及服务中心可达性的指标体系,并采用主成分分析法生成经济韧性指数[7]。Bruneckiene等提出构建包含洞察能力、区域治理能力、知识和创新能力、学习能力、网络和合作能力以及基础设施能力等六个方面的指标体系对经济韧性进行评价[8]。刘晓星等利用117种金融指数测算金融市场系统性风险,使用151种宏观经济指标估计时变脉冲响应,采用风险吸收强度和吸收持续期定量测算宏观经济韧性[5]。

总体看来,指标体系法应用灵活、内涵丰富,可以从宏观经济、产业部门和社会治理等多角度测算符合各自国家和地区特征的经济韧性,具有广泛的应用前景,但无法避免指标选取合理性和可比性较弱的弊端。鉴于此,越来越多的学者采用产值和就业等关键指标的相对变动情况反映经济韧性。Martin等利用过去40年英国主要地区的就业数据,根据实际就业增长率与预期就业增长率的相对变化反映区域经济韧性[9]。Oprea等认为GDP能更好地反映冲击对经济的影响,而且失业率也依赖于GDP,因此将东欧各地区GDP增长率相对于欧洲27国GDP增长率的相对变化反映区域经济韧性[10]。

在肯定产出和就业是反映经济韧性的关键指标的基础上,部分学者开始尝试构建函数模型,利用估计系数度量区域经济韧性。Fingleton等采用英国12个地区1971—2010年的季度就业数据,构建似不相关回归模型测试英国地区就业工程韧性与四次衰退冲击的相关性[11]。Caro利用1992—2012年意大利的区域就业数据和非线性平滑转换自回归模型研究区域经济韧性,提出了一种区分工程韧性和生态韧性的测试方法[12]。Fingleton等基于Dixon-Thirlwal循环因果模型,利用静态凡登定律构建经济增长与就业之间的回归方程,并考虑空间与时间滞后的影响因素,进行GMM-SL-SAR-RE估计,得到真实经济条件与反事实无外部冲击情况的结果差异,以此度量经济韧性[13]。

Christopherson等较早从区域创新体系、生产性基础设施、支持性金融体系,以及多元化经济基础等方面系统探究区域经济韧性的影响因素[14]。此后,学者们主要从人力资本、产业结构、国家和区域政策等方面展开研究。Caro指出意大利南方地区的低经济韧性与该地区人力资本存量较低有关[12]。Brown等认为美国俄亥俄州产业结构多样化的地区在面对经济危机时表现出更强的韧性[15]。Kakderi等建议中央政府为稳定和复苏希腊西马其顿地区所作的努力都应辅之以区域一级的重点政策[16]。

虽然上述研究具有一定启示,但在研究方法、研究内容和研究尺度上仍有待进一步拓展。本文的边际贡献在于:第一,在研究方法上,采用动态空间面板模型、系统GMM和反事实等方法测算城市群经济韧性,科学利用产出和就业两个能够衡量地区经济衰退状况的最具信息量的指标;第二,在研究内容上,采用Dagum基尼系数、核密度估计和空间收敛模型等方法,揭示中国14个城市群经济韧性的地区差异、分布动态和空间收敛特征;第三,在研究领域上,突破行政区划的限制,将区域经济韧性研究置于城市群空间尺度。从理论层面看,本文对于城市群经济韧性的关注有助于城市网络理论与经济韧性理论的融合,推动城市网络韧性研究兴起;从实践层面看,本文对于经济韧性时空格局的关注有助于低韧性城市提高危机意识,推动城市群整体经济韧性进一步提升。

二、研究方法与数据

(一)经济韧性的测算方法

本文借鉴GMM-SL-SAR-RE函数分析法,结合中国城市群实际情况,构建动态空间面板模型,采用系统GMM估计参数,利用反事实法推算就业水平,进而测算城市群经济韧性[13]。具体过程如下:

首先,凡登定律(Verdoorn Law)指出劳动生产率增长与产出增长之间具有线性关系,据此可以利用凡登定律构建经济增长与就业之间的回归方程:

lnyit=α+βlnxit+μi+ηt+εit

(1)

其中,yit为城市i第t年的就业水平,利用单位从业人数与私营和个体从业人数之和表示;xit为城市i第t年的产出水平,利用GDP表示;α和β为待估参数,μi和ηt分别为个体和时间固定效应,εit是随机误差项。

然后,对式(1)进行扩展。由于就业水平具有较强的空间相关性,如果忽视其固有的空间溢出效应很可能得到偏误的实证结果,需要将就业水平的空间滞后项纳入模型,以控制空间相关性。此外,考虑到就业水平可能具有路径依赖特征,即时间滞后效应,需要将就业水平的滞后一期引入标准的静态空间面板模型。因此,本文构建动态空间面板滞后模型(SAR)和动态空间面板误差模型(SEM):

(2)

(3)

其中,ρ为空间相关系数,反映邻近城市的相关变量对本市的影响,wij为空间权重矩阵的元素,其余符号含义与上述一致。

进而,假设各市在危机期间与国家的产出增长率相同,利用全国平均产出增长率估计各市理论上的产出水平,根据式(2)和式(3)的参数估计结果推算出反事实就业水平。公式为:

(4)

(5)

(6)

其中,gNt+1为全国平均产出增长率,其余符号含义与上述一致。

最后,计算出各市的经济韧性。公式为:

(7)

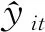
(二)地区差异的测算方法

本文使用Dagum基尼系数方法测算中国城市群经济韧性的地区差异。基本公式如下:

(8)

其中,yji(yhr)表示j(h)城市群内任意城市的经济韧性水平,μ是城市经济韧性水平的均值,n=214,k=14,nj(nh)是j(h)城市群内城市数量。在进行基尼系数分解时,先要依据经济韧性水平的均值对城市群进行排序,即μh≤…≤μj≤…≤μk。根据Dagum基尼系数分解策略,将基尼系数分解为三个部分:城市群内差异贡献Gw、城市群间差异贡献Gnb和超变密度贡献Gt,即G=Gw+Gnb+Gt。

(9)

(10)

(11)

(12)

(13)

(14)

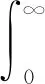
(15)

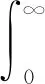
(16)

式(9)和式(10)分别表示j城市群内部的基尼系数Gjj和城市群内部差异贡献率Gw;式(11)和式(12)分别表示j和h城市群之间的基尼系数Gjh和城市群之间差异的贡献率Gnb;式(13)表示超变密度贡献率Gt。其中,pj=nj/n,sj=njμj/nμ,j=1,2,…,k。Djh为j和h城市群之间经济韧性水平的相对影响,具体为公式(14)。djh表示城市群之间经济韧性水平贡献率差值,即j和h城市群之间所有yji-yhr>0的样本值的加权平均,pjh表示超变一阶矩,即j和h城市群之间所有yhr-yji>0的样本值的加权平均,公式分别为式(15)和(16)。Fh(Fj)分别为h(j)城市群的累积密度分布函数。

(三)分布动态的研究方法

本文采用空间核密度估计方法展示中国城市群经济韧性的分布动态。传统核密度估计如式(17)和式(18),随机变量X的密度函数为f(x),N为观测值的个数,K(·)是核函数,Xi为独立同分布的观测值,x为均值,h为带宽。而空间核密度估计是在普通核密度估计的基础上加入时间和空间因素,对随机变量的概率密度进行估计,用连续密度曲线描述随机变量在时空条件下的分布形态,如式(19)和式(20)。f(x,y)是x和y的联合核密度函数,g(y|x)表示在x的条件下y的分布状态。

(17)

(18)

(19)

(20)

空间核密度估计可以从无条件核密度估计、空间静态核密度估计、空间动态核密度估计三个方面揭示中国城市群经济韧性的空间分布形态及其动态演进过程。具体而言,无条件核密度估计用于分析经济韧性从第t年至第t+3年的分布动态;空间静态核密度估计用于分析空间滞后条件下城市群内部经济韧性的相互影响;空间动态核密度估计则分析空间滞后条件下城市群内部其他城市第t年经济韧性对本市第t+3年经济韧性的影响。

(四)收敛性的检验方法

本文采用β收敛模型检验城市群经济韧性的收敛态势。β收敛是指经济韧性较低的城市具有较高的增长率,其与经济韧性较高的城市之间的差距逐渐缩小并最终达到一致的稳态水平。β收敛进一步分为β绝对收敛和β条件收敛。城市群内部要素流动频繁,经济联系密切,存在一定的空间依赖性,应将空间因素纳入收敛模型。因此,本文构建经济韧性β绝对收敛的空间滞后模型和空间误差模型:

(21)

(22)

β条件收敛的空间滞后模型和空间误差模型:

(23)

(24)

其中,Res表示经济韧性,ln(Resit/Resit-1)表示城市i第t年的经济韧性增长速度,μi和ηt分别为个体和时间固定效应,εit是随机误差项,α、β和δ为待估参数,β<0意味着收敛。ρ和λ为空间相关系数,反映邻近地区的相关变量对本地区的影响。wij为空间权重矩阵的元素。X为控制变量,本文选取人力资本(Hum)、技术进步(Tec)、环境规制(Env)、产业结构(Ind)、对外开放(Ope)作为控制变量。其中,利用普通高校在校生人数与年末总人口数之比表示人力资本水平;采用科学支出占财政支出比重作为技术进步的代理变量;使用工业SO2污染强度表征环境规制的反向指标;利用以赫芬达尔——赫希曼指数为基础的熵值法测度产业结构多样化程度[17];采用FDI与GDP的比值表示对外开放程度。

此外,具有相似特征的城市群之间的经济韧性差距同样可能呈现缩小的趋势,即存在俱乐部收敛。一体化发展是城市群内部实现互动合作的基础,而加强互动合作一方面可能带来危机的传递与扩散,另一方面可能增强单个城市的风险抵御能力,因此一体化程度对于城市群经济韧性收敛性的影响具有不确定性。基于上述经济韧性空间收敛模型,以及城市群一体化程度,对中国城市群经济韧性的俱乐部收敛状况进行检验。具体来说,本文借鉴宋迎昌和倪艳亭的研究结果,将城市群分为一体化程度较高、一般和较低三大俱乐部[18](1)一体化程度较高俱乐部包括:珠三角和长三角城市群;一体化程度一般俱乐部包括:京津冀、哈长、山东半岛和辽中南城市群;一体化程度较低俱乐部包括:成渝、武汉、长株潭、环鄱阳湖、中原、北部湾、粤闽浙沿海和关中城市群。。

(五)数据说明

本文研究对象为珠三角、长三角、京津冀、哈长、山东半岛、辽中南、成渝、武汉、长株潭、环鄱阳湖、中原、北部湾、粤闽浙沿海和关中14个城市群。基于数据可获性,选取14个城市群中的214个地级以上城市为研究样本,时间跨度为2008—2019年。城市群所辖城市根据中央和地方出台的城市群发展规划确定。GDP等指标根据价格指数调整为2001年为基期的实际值。个别缺失数值通过插值法补齐。除二氧化硫排放量指标以全市口径近似替代外,其余指标均为市辖区口径。数据来源于历年《中国城市统计年鉴》和各省市统计年鉴。

三、经济韧性测算

(一)空间面板模型的估计结果

在对空间面板模型进行参数估计之前,一方面需要对被解释变量就业水平的空间相关性予以检验,另一方面需要对空间滞后模型和空间误差模型这两个竞争性模型进行比选。

通常采用Moran指数判断变量是否存在空间相关性。Moran指数介于-1到1之间,大于0表示变量具有空间正相关性,小于0表示变量具有空间负相关性,等于0表示变量不存在空间相关性。本文采用逆标准地理距离空间权重矩阵检验就业水平的空间相关性。表1显示Moran指数在观测期内均显著为正,表明城市就业水平具有空间正相关性,同时也验证将空间因素纳入分析框架的必要性。

空间滞后模型和空间误差模型的比选工作通常由LM检验来完成,其判断标准为:LM统计量更显著的模型为更合意的模型,若两种模型的LM统计量具有相同的显著水平,那么就需要由稳健型LM统计量的显著性来确定模型的设定形式。由表2可知,针对空间滞后模型的LM检验值至少在5%的水平上显著,而针对空间误差模型的LM检验值并不显著,从而表明空间滞后模型要优于空间误差模型。

表2 经济韧性测算模型参数估计结果

将被解释变量的滞后项纳入实证模型易导致内生性问题,此时利用系统GMM估计动态空间面板模型往往较传统的极大似然估计更为有效。因此本文采用系统GMM对式(2)进行估计,结果如表2所示。就业水平的时间滞后项系数显著为正(β0=0.419 5,P=0.000),表明城市就业存在“循环累积”效应;产出对就业具有显著的正向影响(β1=0.142 0,P=0.008),符合凡登定律;就业水平的空间滞后项系数显著为正(ρ=0.392 0,P=0.000),表明城市之间就业水平具有正向空间溢出效应。进而利用式(4)和式(6)估计出反事实就业水平,最后利用式(7)计算出14个城市群214个城市2008—2019年的经济韧性。

(二)经济韧性的测算结果

横向对比14个城市群的经济韧性,结果如表3所示。一方面,2008—2019年的经济韧性均值排名反映出,珠三角等10个城市群经济韧性大于1,表明这些城市群实际就业水平超过了反事实就业水平,具有更强的经济韧性;而成渝等4个城市群的经济韧性小于1,表明受到国际金融危机冲击后,就业水平恢复较慢,经济韧性较弱。另一方面,整体看来,东部城市群(珠三角、辽中南、粤闽浙沿海和长三角)在前5名中占据4席,表现出更强的经济韧性。

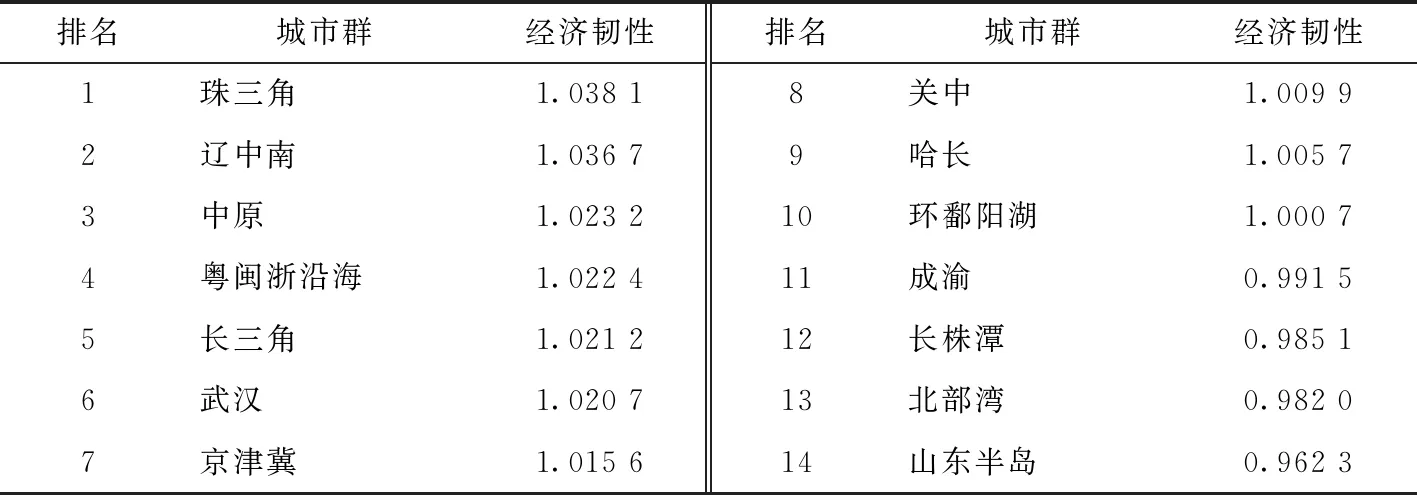
表3 2008—2019年14个城市群经济韧性均值排名

纵向对比2008—2019年经济韧性的变动趋势,结果如图1和表4所示。一方面,整体看来,中国城市群经济韧性变动趋势呈现N型特征,2008—2011年上升趋势明显,2011—2017年波动下降,2017—2019年再次回升。这表明中国中央政府于2008年适时出台应对国际金融危机的一揽子计划在短期内提高了城市群抵抗冲击的能力。但随着中国经济步入新常态,投资拉动经济复苏的能力减弱,导致城市群经济韧性有所下降。而“十三五”期间中国坚定实施扩大内需战略,发挥城市群要素配置效率优势和一体化市场潜力优势,促进城市群经济韧性再次回升。另一方面,观察14个城市群经济韧性的变动趋势可以发现,粤闽浙沿海、关中、成渝和山东半岛呈现N型特征;珠三角、中原、长三角和环鄱阳湖呈现倒U型特征;哈长呈现倒N型特征;武汉和长株潭呈现下降趋势;辽中南、京津冀和北部湾呈现上升趋势。

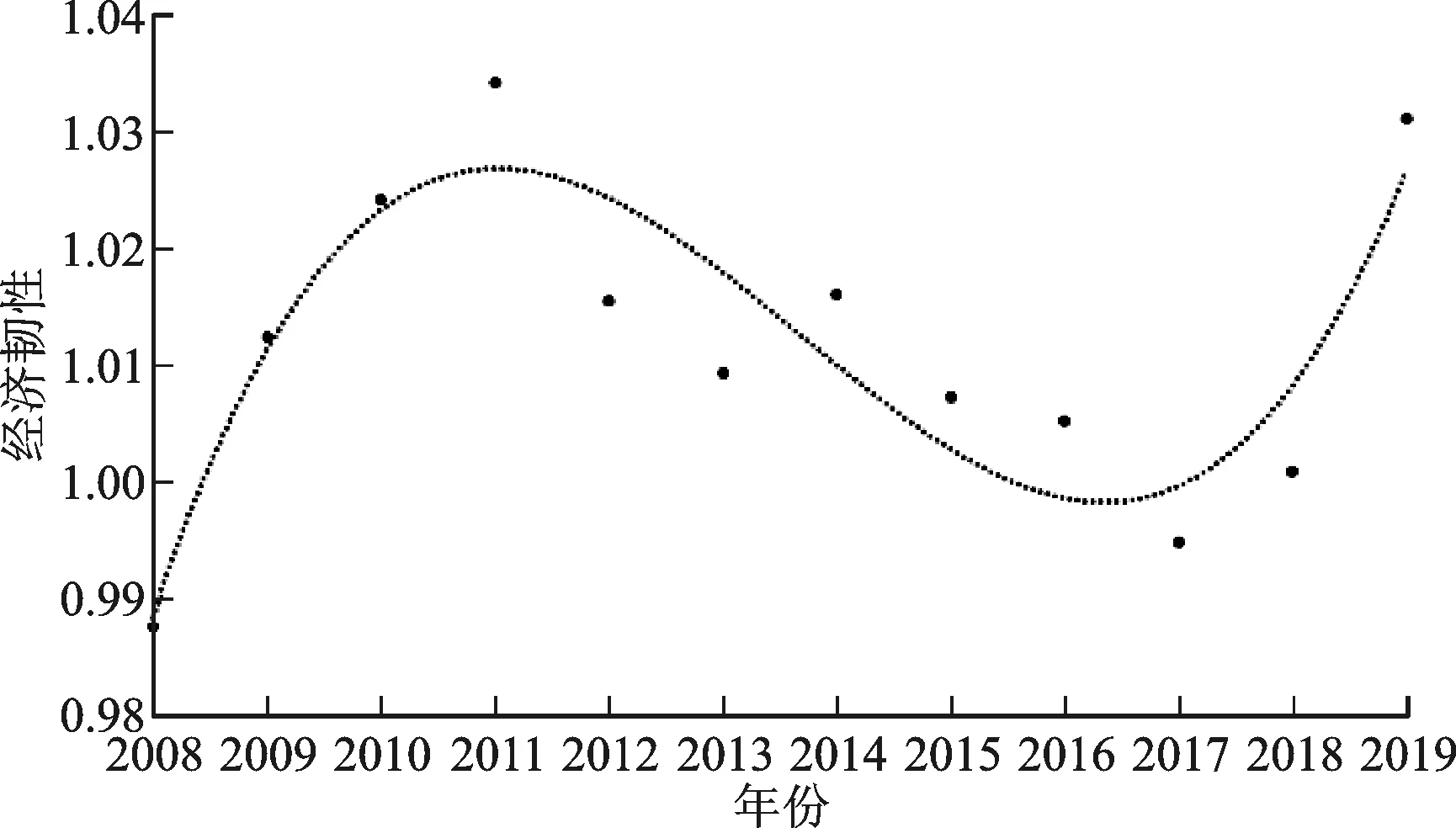
图1 2008—2019年城市群经济韧性变动趋势

表4 2008—2019年14个城市群经济韧性变动趋势

四、地区差异分析

(一)城市群内部经济韧性差异

表5报告了14个城市群内部经济韧性Dagum基尼系数的计算结果。横向对比城市群内部经济韧性的基尼系数可以发现,成渝、环鄱阳湖、长三角和北部湾的基尼系数较高,观测期内的均值分别达到0.103 0、0.091 8、0.083 2和0.080 6,表明经济韧性在城市群内部的不均衡现象明显。成渝、环鄱阳湖和北部湾经济韧性发展不均衡的主要原因是成都、南宁和南昌等核心城市的极化效应十分明显,而长三角主要原因是广义城市群(苏、浙、皖、沪41个城市)范围内边缘城市的长尾效应十分明显。珠三角和山东半岛的基尼系数则相对较低,分别为0.054 5和0.059 7,体现出省域范围内的城市群可能在经济韧性方面具有更小的差距。纵向对比城市群内部经济韧性的基尼系数可以发现,珠三角、中原、关中和北部湾的变动趋势呈现U型特征,粤闽浙沿海和环鄱阳湖呈现倒U型特征,长三角和山东半岛呈现倒N型特征,长株潭呈现N型特征,武汉、京津冀、哈长和成渝具有上升趋势,而辽中南具有下降趋势。其中,珠三角和辽中南在观测期内年均变动幅度最大,分别为0.079 7和-0.044 4。

(二)城市群之间经济韧性差异

表6报告了14个城市群之间经济韧性Dagum基尼系数的年度均值和变动幅度排名前十位和后十位情况。从年度均值方面看,成渝与其他城市群之间的经济韧性差距较大,在前十位中占据8席;而珠三角与其他城市群之间的经济韧性差距较小,在后十位中占据6席。结合表5可知,成渝和珠三角分别为经济韧性内部差距最大和最小的城市群,两个城市群内部所表现出的极化和均衡现象也间接影响了城市群之间的经济韧性差距。从变动幅度方面看,京津冀与其他城市群之间的经济韧性差距增幅较大,在前十位中占据8席;而北部湾与其他城市群之间的经济韧性差距降幅较大,在后十位中占据6席。结合表3和表4可知,京津冀相对富有韧性,而北部湾相对缺乏韧性,但两个城市群经济韧性都具有明显的上升趋势,因此表现出京津冀扩大领先优势,而北部湾缩小落后差距的现象。

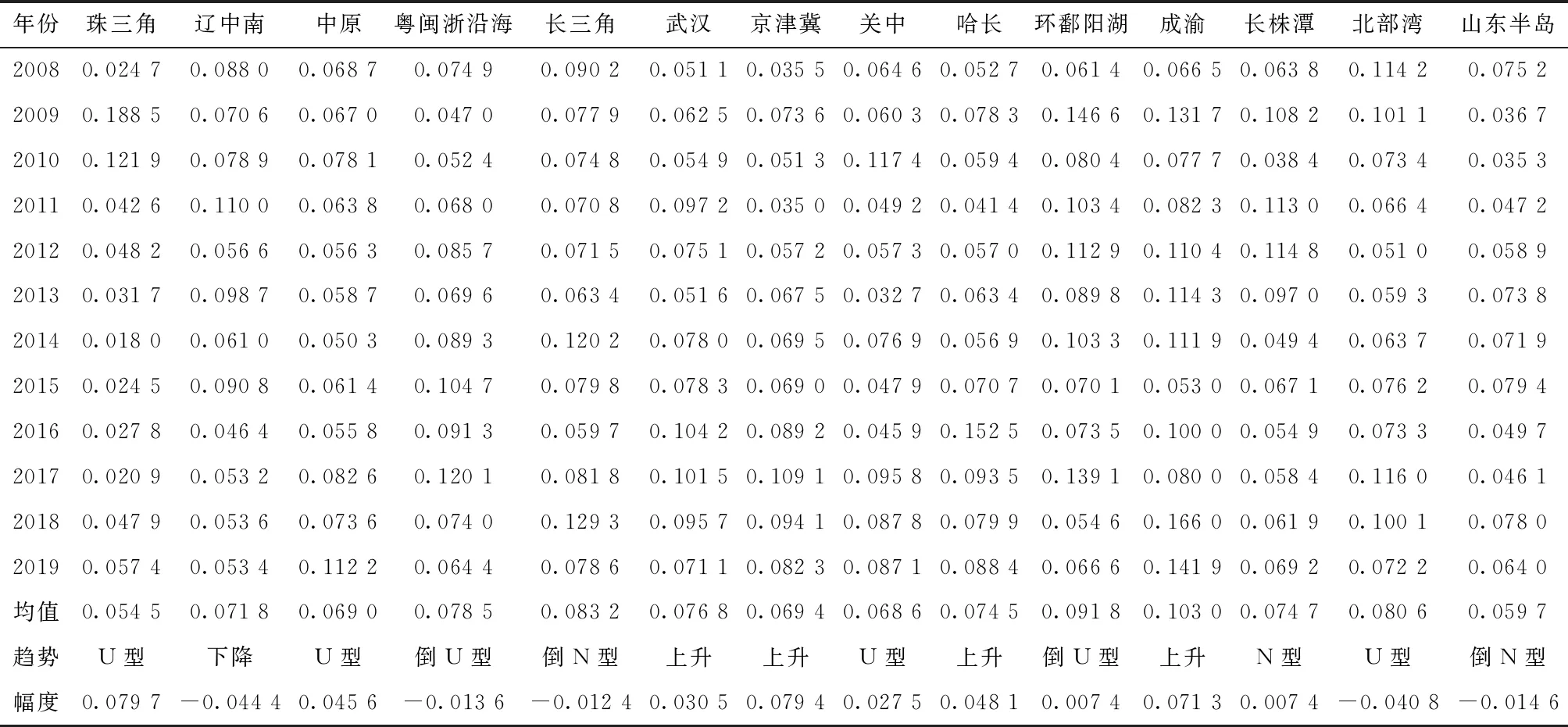
表5 2008—2019年14个城市群内部经济韧性基尼系数

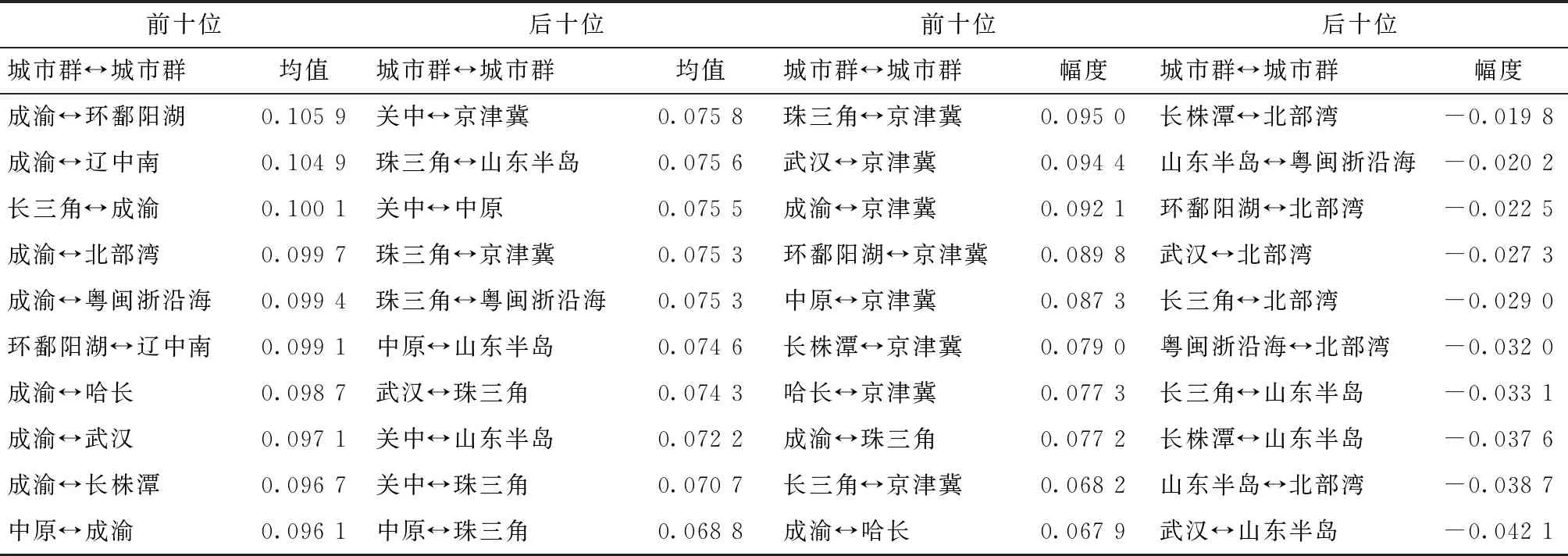
表6 2008—2019年14个城市群之间经济韧性基尼系数

(三)城市群经济韧性总体差异及其分解

表7报告了14个城市群总体Dagum基尼系数及其分解结果。总体上看,观测期内中国城市群经济韧性Dagum基尼系数呈现波动上升的趋势,年均增幅为0.019 1,表明城市群经济韧性差距有所扩大。从差异来源看,观测期内城市群内部、城市群之间和超变密度的贡献率的均值分别为9.011%、18.945%和72.044%,体现出城市群间交叉重叠部分对总体差距的影响十分明显。从差异分解的变动趋势方面看,城市群内部差异贡献率变动趋势相对平稳,年均增幅仅为0.003 4;城市群之间差异贡献率上升趋势明显,年均增幅达到0.073 2;而超变密度的贡献率下降趋势明显,年均降幅达到-0.019 2。可以发现,在超变密度对城市群经济韧性地区差距贡献率居于主导地位的同时,城市群之间经济韧性的差距扩大趋势不容忽视。

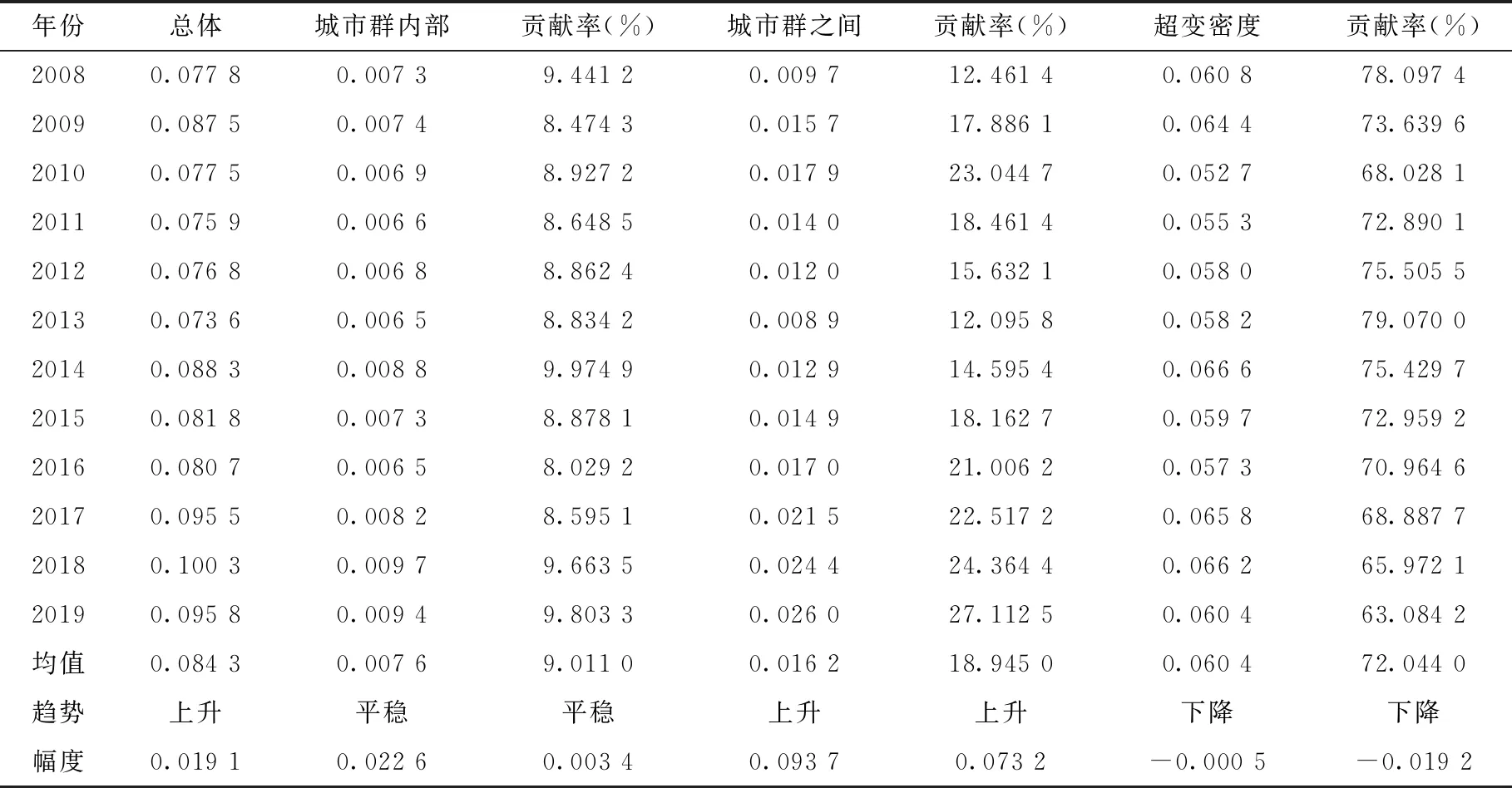
表7 中国城市群经济韧性基尼系数及其分解

五、分布动态分析

(一)无条件核密度估计

图2(a)和(b)展示了中国城市群经济韧性分布的无条件核密度和密度等高线。其中,X轴为第t年的经济韧性,Y轴为第t+3年的经济韧性,垂直于XY平面的Z轴为核密度,表示在XY平面内每一点的概率密度,平行于Y轴的线表示从X轴的点到Y轴上任一点的概率密度,描述了从第t年到第t+3年城市群经济韧性分布变化的转移概率。如果等高线集中分布于正45度对角线附近,说明第t+3年的经济韧性分布和第t年相一致;如果等高线集中分布于负45度对角线附近,说明经济韧性发生了转变,从第t年到第t+3年经济韧性水平高(低)的城市群转变为低(高)的城市群。观察图(b)可知,密度等高线集中于正45度对角线附近,说明从第t年到第t+3年中国城市群经济韧性的分布状态变化较小。同时也可以发现,等高线整体水平偏低,表明中国城市群经济韧性提升速度较慢。

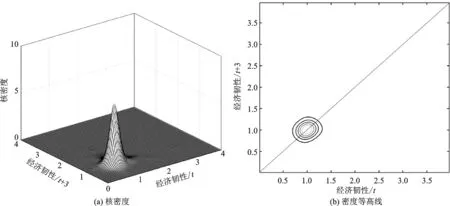
图2 经济韧性的无条件核密度和密度等高线

(二)空间静态核密度估计

图3(a)和(b)展示了中国城市群经济韧性分布的空间静态核密度和密度等高线。空间静态核密度估计可以进一步考察经济韧性分布状态的空间相关性。X轴为城市群内其他城市经济韧性,计算方法为:以本市与城市群内其他城市的逆标准地理距离为权重,加权平均其他城市的经济韧性;Y轴为本市经济韧性。如果经济韧性存在空间相关性,当表现为低—低、高—高集聚现象时,密度等高线会集中分布于正45度对角线附近;当表现为高—低集聚现象时,则密度等高线会集中分布于负45度对角线附近。观察图(b)可知,中国城市群经济韧性集中分布于正45度对角线附近,呈现低—低、高—高集聚的正向空间相关性。同时可以发现,等高线逐渐向45度对角线上方偏移,表明随着城市群内其他城市经济韧性的提高,空间溢出效应促进本市经济韧性趋于提高。

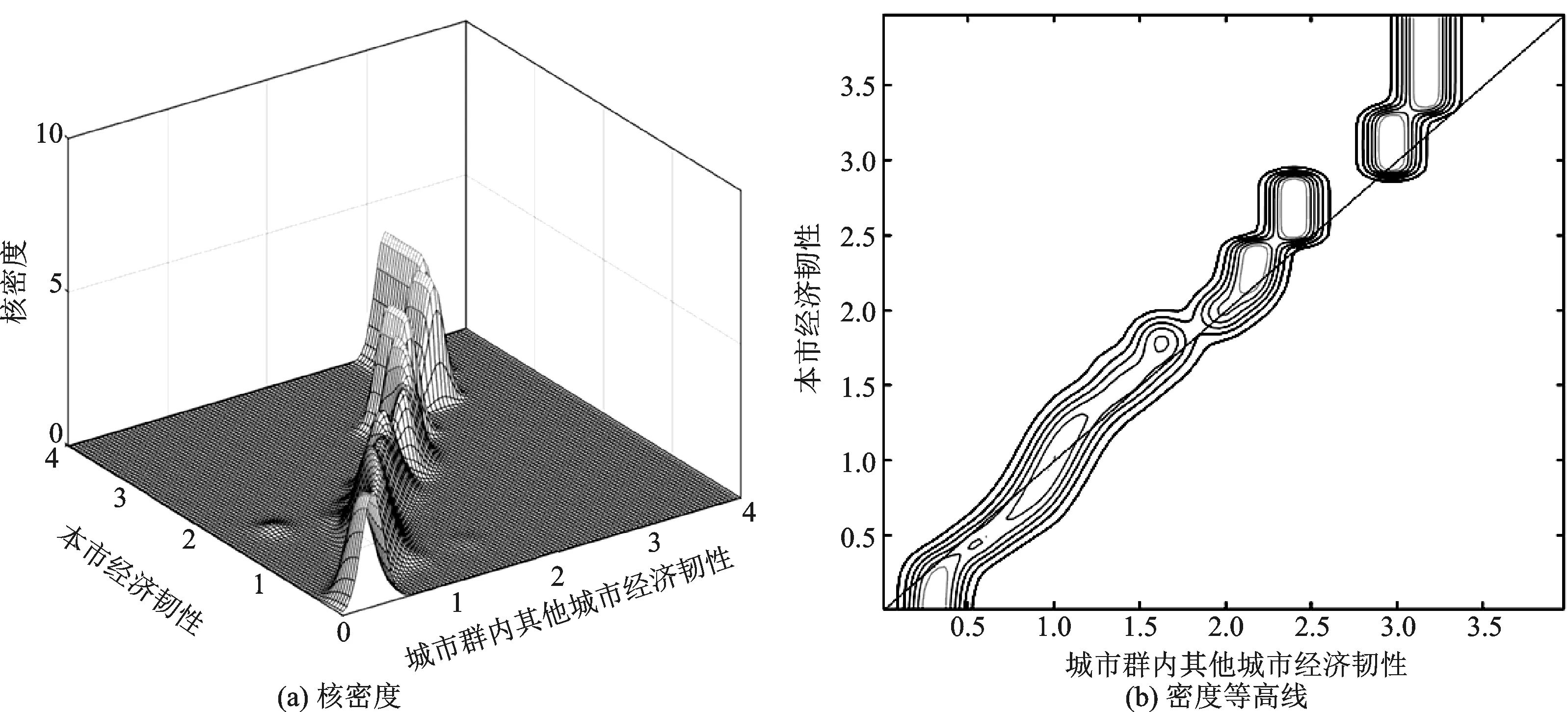
图3 经济韧性的空间静态核密度和密度等高线

(三)空间动态核密度估计

为进一步揭示中国城市群经济韧性是否具有空间动态效应,本文分别从总体以及14个城市群角度分析空间滞后条件下,第t年城市群内其他城市经济韧性对第t+3年本市经济韧性分布动态的影响,结果如图4所示(2)限于篇幅,仅报告了密度等高线的分布情况。。一方面,观察城市群总体密度等高线的分布情况。从形态上看,密度等高线呈现出平行于Y轴的特征,体现出第t年城市群内其他城市经济韧性对第t+3年本市经济韧性的影响并不明显;从波峰上看,密度等高线的核心处于正45度对角线上方,体现出经济韧性具有向高水平转变的趋势。另一方面,观察14个城市群密度等高线的分布情况。从形态上看,京津冀、关中、哈长、长株潭、北部湾和山东半岛的密度等高线大体分布于正45度对角线附近,表明本市与城市群其他城市的经济韧性呈现正向空间动态溢出效应;而辽中南、中原、粤闽浙沿海、长三角、环鄱阳湖和成渝的密度等高线具有向负45度对角线转向的趋势,表明当本市经济韧性发展到较高水平时,可能受到来自城市群内其他城市的负向空间动态溢出效应的影响。从波峰上看,中原、武汉和哈长经济韧性表现出单峰分布,且处于正45度对角线上方,体现出经济韧性具有向高水平转变的趋势。

图4 经济韧性空间动态核密度等高线

六、空间收敛分析

在对模型模型(21)～(24)进行参数估计之前,同样需要对被解释变量经济韧性增长速度的空间相关性予以检验,以及对SAR和SEM模型进行比选。Moran指数显示经济韧性增长速度具有空间正相关性,模型比选结果在表8～10中展示。

(一)β绝对收敛

表8报告了城市群总体和14个城市群经济韧性β绝对收敛检验结果。首先,总体而言,LM检验结果支持采用SEM模型,且λ显著为正,表明城市群内部相邻城市之间经济韧性的空间正向关联较强。经济韧性的收敛系数β显著为负,表明城市群经济韧性存在β绝对收敛趋势。其次,各城市群而言,LM检验结果支持珠三角、辽中南、中原、武汉、京津冀和环鄱阳湖采用SEM模型,长三角采用SAR模型,而其他城市群不适用空间面板模型。可以发现经济韧性水平较高的城市群内部空间关联性也较强,表明城市之间的互动合作有利于提升城市群整体经济韧性。14个城市群经济韧性的收敛系数β均显著为负,在人力资本、技术进步、环境规制、产业结构和对外开放等影响因素相似前提下,各城市群内部城市经济韧性均会向各自稳态水平收敛。最后,对比各城市群的收敛系数,可以发现珠三角的收敛系数最大(β=-1.344 5),而山东半岛的收敛系数最小(β=-0.958 1),意味着经济韧性水平最高的珠三角具有最快的收敛速度,而经济韧性水平最低的山东半岛具有最慢的收敛速度,体现出经济韧性较低的城市能否尽快追赶上经济韧性较高的城市,不仅影响了城市群整体的经济韧性水平,也影响了城市群之间的经济韧性差距。

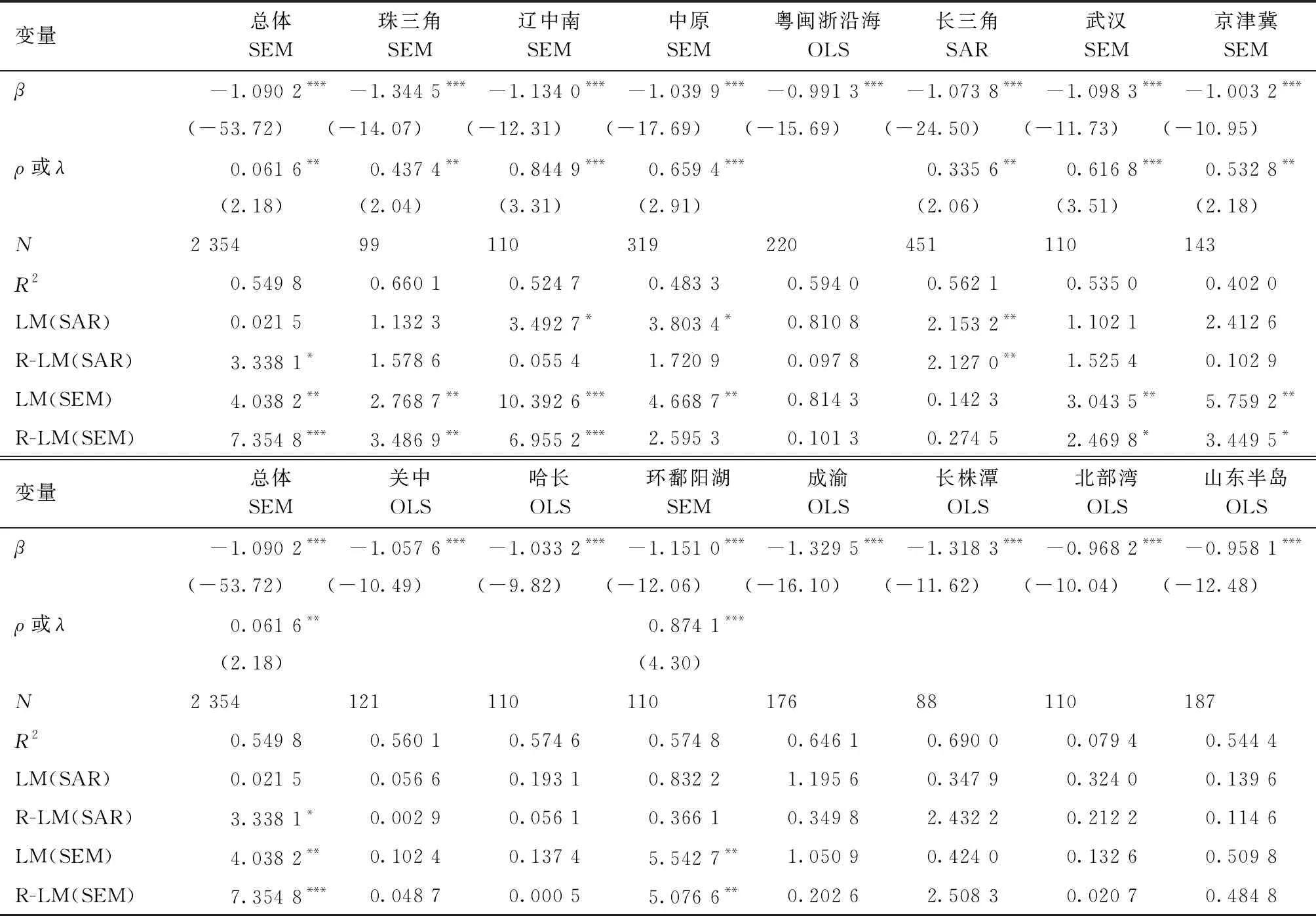
表8 城市群经济韧性的β绝对收敛检验

(二)β条件收敛

本部分考察城市群经济韧性在考虑一系列控制变量后的收敛趋势,结果如表9所示。城市群总体和14个城市群收敛系数β均显著为负,表明存在β条件收敛趋势,意味着在考虑了除初始值以外的其他异质性影响因素情况下,城市群经济韧性朝着各自稳态水平变化发展。从控制变量的表现看,城市群总体回归模型显示,人力资本、技术进步和产业结构对经济韧性增长速度具有显著的正向影响,而环境规制和对外开放的负向影响并不显著。人力资本和技术进步是一个地区在冲击后进行适应性动态调整的基础,劳动力素质越高、创新能力越强的城市群越能在冲击后的更迭期发展“新经济”部门。产业结构多样化有利于降低经济发展的不稳定性,同时分散冲击带来的风险,减少整体经济损失。对各城市群而言,控制变量对城市群经济韧性增长速度的影响具有异质性。例如,以反向指标环境污染强度表征的环境规制对中原和环鄱阳湖经济韧性增长速度的促进作用较为显著,启示其他城市群在可持续发展理念指导下提高环境质量,即使遭受危机冲击也有创造新的发展路径的环境基底。对外开放在粤闽浙沿海和长三角的负向影响更为显著,体现出对外依赖程度可能是城市群经济韧性差异的重要原因,东部地区城市群在引进外资方面存在区位优势,但也强化了其与国际市场的关联,国际金融危机等冲击将降低其经济韧性。

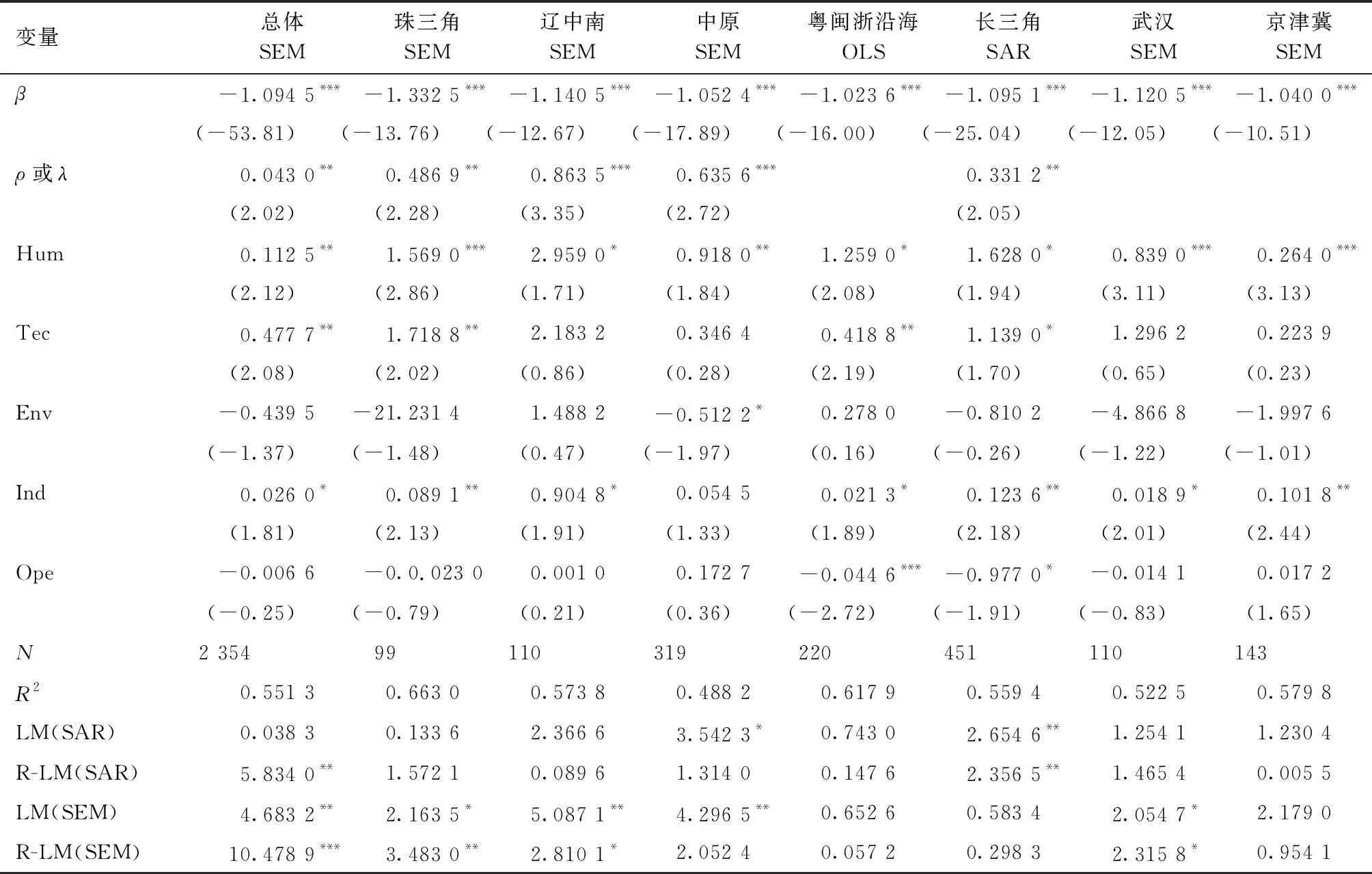
表9 城市群经济韧性的β条件收敛检验

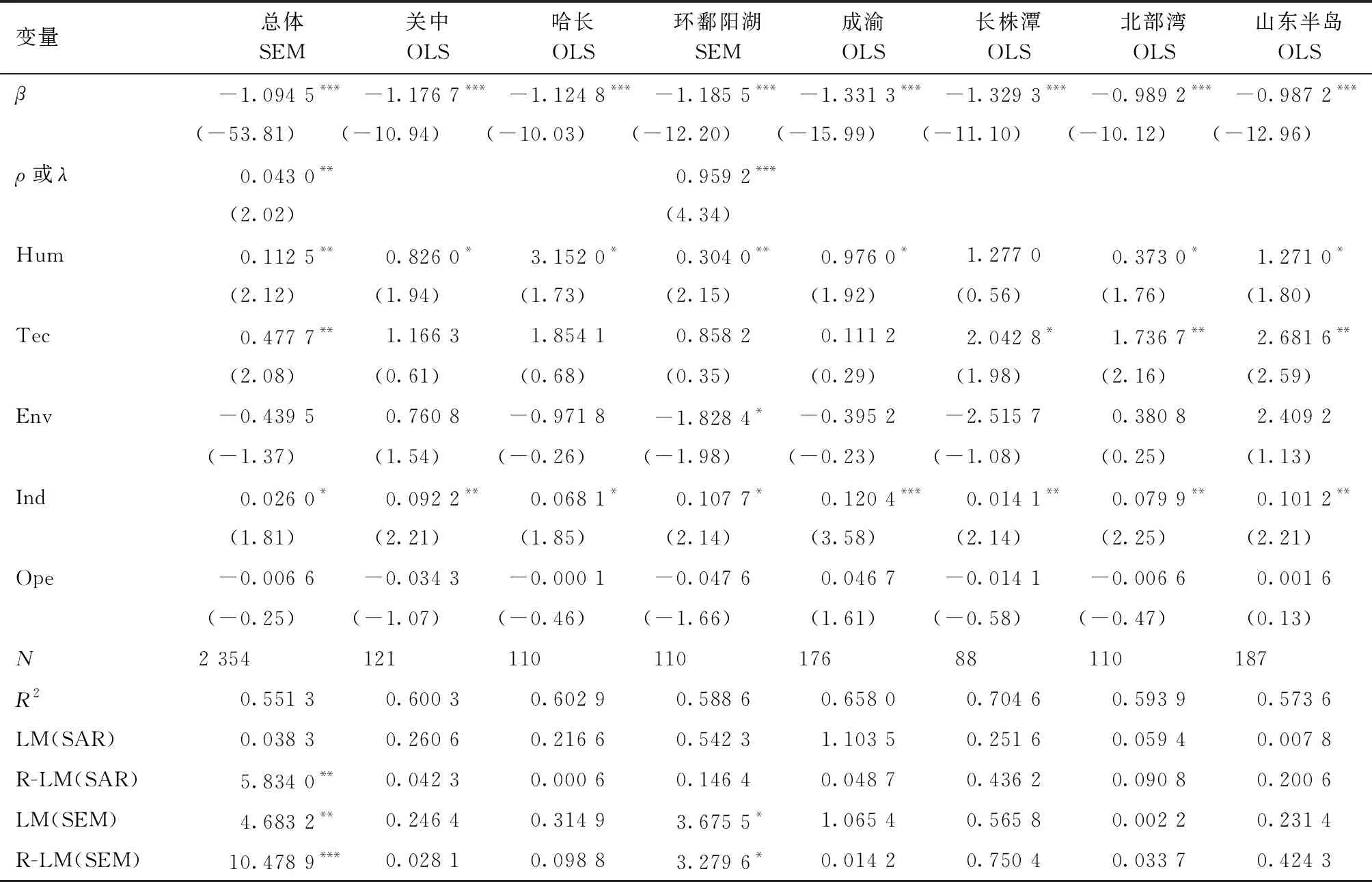
表9 城市群经济韧性的β条件收敛检验(续)

(三)俱乐部收敛

考虑一体化程度对城市群经济韧性收敛性可能带来的影响,本文将14个城市群根据一体化程度划分为三大俱乐部进行分组检验,结果如表10所示。首先,三大俱乐部内部经济韧性的空间相关性较为明显,表明发展水平相近的城市群之间更容易产生互动合作。其次,从经济韧性收敛系数方面看,三大俱乐部均存在显著的俱乐部收敛趋势,其中一体化程度较高的城市群具有更快的收敛速度,反映出提高城市群内部的互动合作更有利于构建韧性城市体系,增强共同抵御风险的能力。最后,从控制变量方面看,人力资本和技术进步在三大俱乐部的正向影响仍然显著,而产业结构在一体化程度较低城市群的正向影响并不显著。可能原因在于城市产业结构多样化需要更大的市场范围,城市群一体化发展为城市各类型产业提供了“借用”其他城市规模的机会,而一体化程度较低的城市群难以整合市场,不利于发挥多样化产业结构分散风险、提升经济韧性的能力。

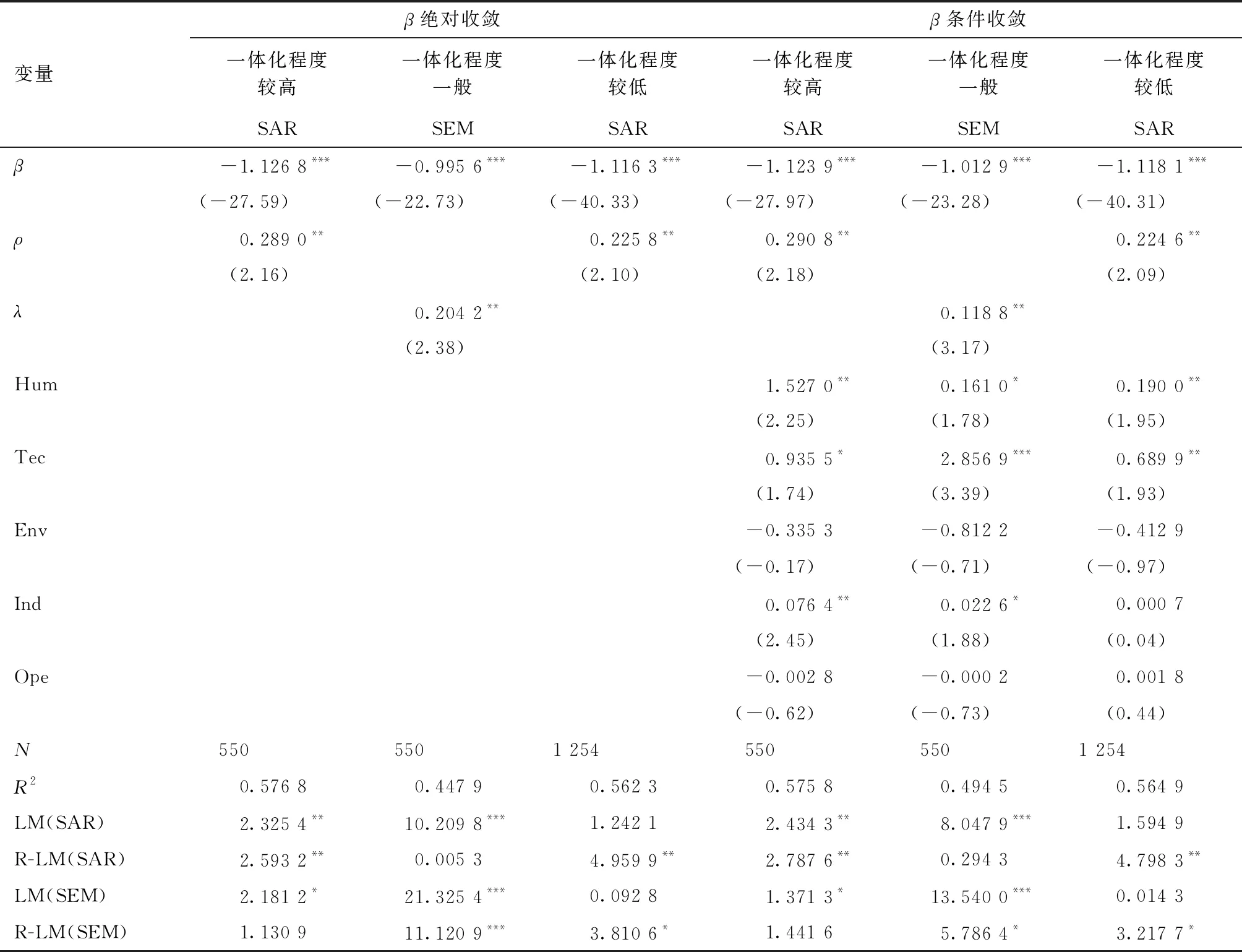
表10 城市群经济韧性的俱乐部收敛检验

七、结论与政策建议

本文利用2008—2019年数据,基于动态空间面板模型、系统GMM和反事实法测算中国14个城市群的经济韧性,采用Dagum基尼系数对城市群经济韧性的差异进行测算与分解,运用核密度估计方法刻画城市群经济韧性的分布动态特征,利用空间收敛模型对城市群经济韧性的β收敛趋势进行检验。研究发现:

首先,经济韧性测算结果表明,珠三角等10个城市群的经济韧性较强,而成渝等4个城市群的经济韧性较弱;东部地区城市群的经济韧性相对较强;城市群经济韧性整体变动趋势呈现N型特征。其次,Dagum基尼系数及其分解结果表明,城市群经济韧性Dagum基尼系数呈现波动上升的趋势,城市群经济韧性差距有所扩大;成渝内部以及与其他城市群之间的经济韧性差距均较大,而珠三角内部以及与其他城市群之间的经济韧性差距均较小;超变密度对城市群经济韧性地区差距的贡献率居于主导地位,而城市群之间经济韧性的差距具有扩大趋势。然后,核密度估计结果表明,城市群经济韧性的分布状态变化较小,且提升速度较慢;城市群经济韧性呈现低—低、高—高集聚的正向空间相关性;京津冀等城市群经济韧性呈现正向空间动态溢出效应,而辽中南等城市群经济韧性发展到较高水平时呈现负向空间动态溢出效应。最后,空间收敛性的检验结果表明,城市群总体以及各城市群经济韧性均存在β绝对收敛,其中珠三角的收敛速度最快,而山东半岛的收敛速度最慢;城市群总体和各城市群同时存在β条件收敛,人力资本、技术进步和产业结构对经济韧性增长速度具有显著的正向影响;一体化程度相似的城市群经济韧性表现出俱乐部收敛趋势,而且一体化程度较高的城市群具有更快的收敛速度。

基于上述结论,本文提出以下政策建议:

一是加强互动合作,缩小城市群经济韧性差距。针对城市群内部和城市群之间经济韧性差距明显的问题,一方面,长三角等富有韧性但内部差距明显的城市群,应该发挥核心城市的示范带动作用,加快低韧性城市向高韧性城市收敛;珠三角等富有韧性且内部相对均衡的城市群,应当继续保持内部城市协同发展态势;成渝等缺乏韧性且内部差距明显的城市群,应警惕城市间因负向溢出效应导致的危机转嫁与蔓延;山东半岛等缺乏韧性但内部相对均衡的城市群,应当着力培育更具韧性的经济增长极,然后在扩散效应的作用下带动整体经济韧性的提升。另一方面,成渝、长株潭、北部湾、山东半岛等经济韧性较低的城市群应在人才交流、技术引进和产业转型等方面与其他城市群加强合作,吸收先进经验,从而缩小城市群之间经济韧性的差距。

二是深化网络协同,提高城市群风险抵御能力。针对目前仍有城市群经济韧性不具有空间动态效应,甚至存在负向空间动态效应的问题,一方面,虽然珠三角和武汉城市群的空间动态效应均不明显,但珠三角得益于内部相对均衡的发展态势仍能保持较高的韧性水平。而武汉城市群内部低韧性城市较多,因此更加需要深化产业网络协同,通过优化产业链布局,整合各市优势资源,增强低韧性城市风险抵御能力,发挥正向空间溢出效应对于增强城市群就业承载力和产出稳定性的关键作用。另一方面,辽中南、中原、粤闽浙沿海、长三角、环鄱阳湖和成渝城市群需要深化政策网络协同,通过危机防御政策的合作创议、合作制定、合作执行,一体化推进城市群应对各类危机的政策实施效力,阻止负向空间溢出效应加剧危机在城市群内部的扩散。

三是坚持多元发展,增强城市群长期调适能力。针对在一体化程度更高的城市群,多样化产业结构更有利于提高经济韧性这一现象。一方面,需要坚持产业多元化发展道路,大城市凭借制造业基础积极发展现代服务业,利用产业协同集聚优势激发产业间的创新活力,为后危机时期适应性调整提供创新动力;中小城市应积极参与城市群协同分工,克服对单一产业的过度依赖,积极探索多元发展的增长路径。另一方面,需要在一体化市场中发挥借用规模效应,通过构建要素和产品自由流通和高效配置的城市群一体化市场体系,促进城市间“互借”市场规模,充分挖掘市场潜力,进而实现在内循环为主体的空间格局下促进多元产业良性发展;同时注意规避城市网络关联下危机扩散效应可能对一体化市场的潜在破坏,进一步增强城市群网络韧性。