基于时频谱相似度全并联AT牵引网行波测距方法

舒新星，陈剑云，华 敏，傅钦翠

(华东交通大学 省部共建轨道交通基础设施性能监测与保障国家重点实验室，江西 南昌 330013)

截至2021年底,全国高速铁路运营里程已达到4万km，快速准确定位故障点对保证铁路安全运行具有重要意义。现有牵引网故障测距装置以阻抗测距原理为主[1-2]，但受过渡电阻、系统运行状态等影响，难以保证其良好稳定的测量精度[3]。行波法因其测距算法简单、测量精度高等优点，基于行波法的测距装置已广泛运用于电网实际运行中[4]，行波法将在牵引供电系统中得到更多的研究和运用。

全并联AT牵引网因其具传输功率大、供电距离长和电压损耗低等优点已成为当前高速铁路及客运专线的主要供电方式[5]。与三相电力对称线路相比，其线路不对称，阻抗不连续点多；接触线由长1.5 km左右的锚段联结而成，锚段会延缓初始行波上升速度[6]；钢轨传输丰富的行波信号，钢轨频变参数比较明显[7]；机车整流产生的谐波和过电分相产生的过电压会对行波的识别产生干扰以及行波在传播过程中发生色散现象[8]，上述不同使行波在牵引网线路上的传播更为复杂且波头衰减严重。

为解决上述问题，诸多学者进行了大量研究。一种思路是采用信号处理方法提高行波波头检测和标定的能力，例如小波变换[9]、形态学[10]、希尔伯特-黄变换[11](HHT)和变分模态分解[12](VMD)等，但全并联AT牵引网机车谐波和干扰源多，仅依靠信号处理方法远远不够，采集并选择合适的原始数据能够提高波头检测和标定的有效性。另一种思路是在线路上加多个监测点[13]，多点信息融合可避免故障信息遗失，但其多端数据采集需要同步对时，且如果测量点的设置没有结合全并联AT牵引网行波的传播规律将产生大量无用数据。上述两个方面仅仅笼统的利用多端点信息，并采用相关信号处理方法检测和标定行波波头进行故障测距，但没有通过详细分析各监测点原数据波形的特性来选择奇异性更优的测量点数据，造成错标和漏标波头的情况时有发生。

鉴于此，为解决全并联AT牵引网线路电压、电流分布复杂而增加故障定位难度的问题，本文将从以下两个方面去解决：一方面是当故障发生在不同区段时供电臂首末两端哪端电流、电压行波波形奇异性更强，更有利于被检测标定；另一方面是采用何种方法来判断选用首末哪个端的电流、电压行波用于单端测距。第一个问题可以通过以下三点来解决：①对牵引网线路进行建模并解耦；②AT自耦变压器在不同联结方式和不同等效电容下对暂态行波传播的影响；③供电臂首末两端的暂态电流波形中各个波头传播路径的理论和仿真波形图分析行波传播规律。全并联AT牵引网线路中，故障发生在不同区段时，供电臂首端上下行线路之间的波形相似程度不同，两个波形的相似度可以通过计算波形之间的时频谱相似度来判断，因此通过计算首端上下行线路电流行波波形的时频谱相似度矩阵可解决第二个问题。根据上述两个方面，提出基于时频谱相似度全并联AT牵引网行波测距方法。通过仿真验证各种短路故障类型和使用实测数据验证该方法，并与 2019年10月24日昌赣赣县北供电臂基于“吸上电流比”现场测距结果进行对比，本文方法具有更好的准确度。

1 全并联AT牵引网故障行波传播规律分析

要解决当故障发生在不同区段时供电臂首末两端哪一端电流、电压行波波形奇异性更强，更有利于被检测标定的问题，就必须从分析全并联AT牵引网的行波传播规律开始。全并联AT牵引网线路不对称，且由AT自耦变压器连接上下行，使其线路电压、电流分布复杂。因此，可采用相模变换矩阵对线路解耦、分析AT自耦变压器对行波传播的影响和线路上电流行波的传播路径达到目的。

1.1 全并联AT供电牵引网建模与相模变换

全并联AT牵引网由承力索MW、接触线CW、正馈线PF、保护线PW和钢轨R以及上下行共12根平行导体组成，各导线参数见表1。

表1 导线类型及主要参数

导线合并规则：将接触导线和承力索等效为二分裂导线；钢轨等效为架空线路，将两根钢轨和保护线合并成一条等值钢轨，全并联AT牵引网等效为六相等值相导线，如图1所示。每条供电臂长25～30 km[5]，自耦变压器将其分为两区段，设AT0～AT1段距离为L1，AT1～AT2段距离为L2。

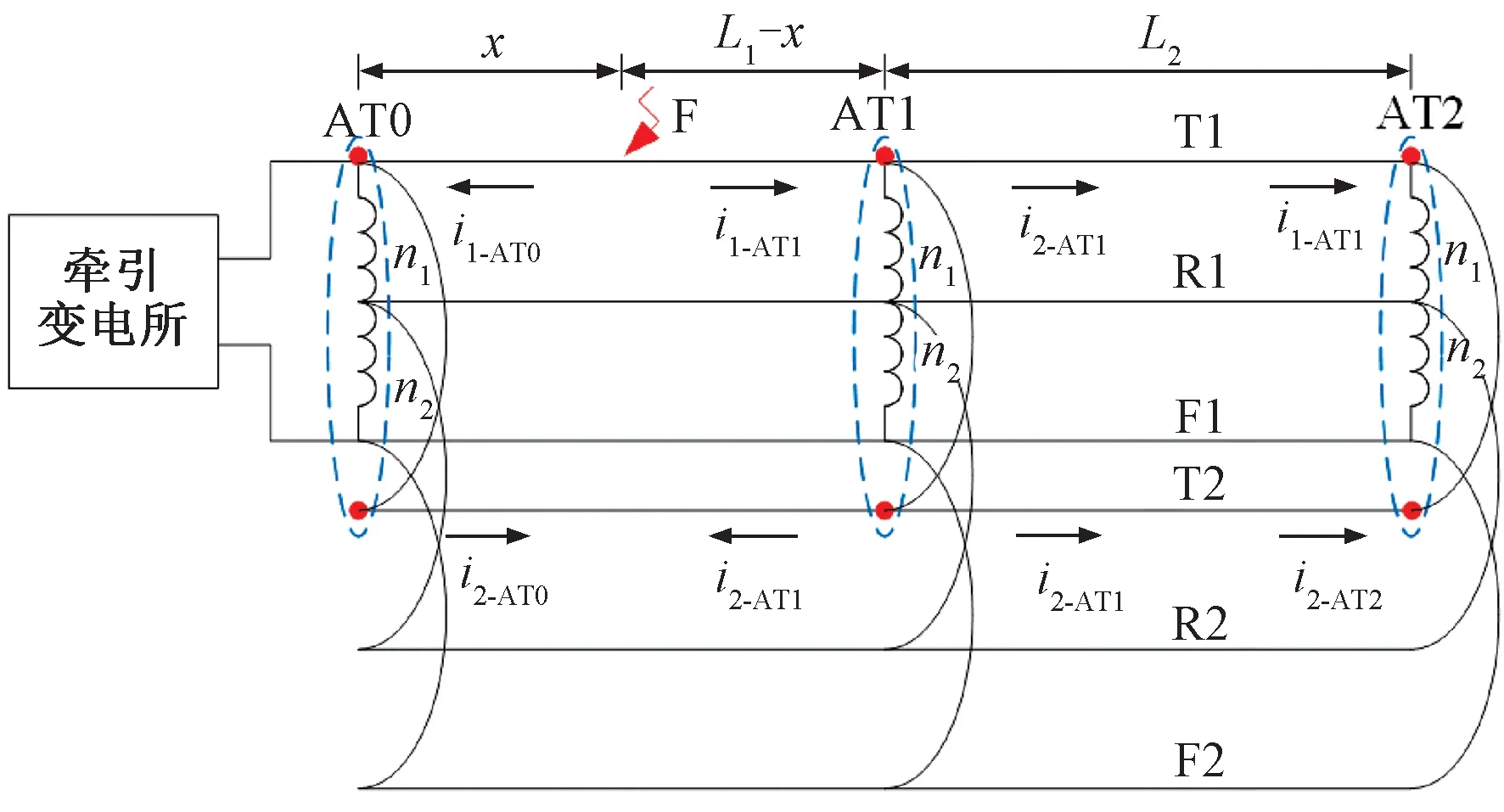
图1 全并联AT牵引网及T-N故障行波传播路径

按导线等效合并规则和表1各导线参数输入EMTP线路模型中可得到不同频率下的电流相模变换矩阵和各模量的衰减系数与模速度。故障行波频率范围大，当频率大于工频时，可认为相模变换矩阵与频率无关[14]，采用5 kHz下经过实数化后的电流相模变换矩阵为

( 1 )

全并联AT牵引网各模量的衰减系数和相位速度见表2。可得出零模衰减系数大，模速低且不稳定；线模分量的衰减系数小且线模速度接近光速并且稳定。

表2 各模量的衰减系数和模速度

1.2 全并联AT自耦变压器对行波传播的影响

AT自耦变压器为牵引网纵向元件，所以分析其对行波的影响是必要的。一方面，AT自耦变压器连接上下行线路形成阻抗不连续点，行波会发生折反射。通过仿真上下行不同联结方式分析其对行波传播的影响，其波形如图2(a)、图2(b)所示。另一方面，分析AT自耦变压器本身对行波的影响，理想情况下可将自耦变压器绕组视为开路[15]，认为自耦变压器对行波的传播没有影响，但AT所设备对地电容对行波会有影响[16]，对故障行波经过单线牵引网切除AT和AT并联电容大小分别为0、0.000 1、0.001、0.005、0.01pF的各种情况进行仿真，如图2(c)、图2(d)所示。

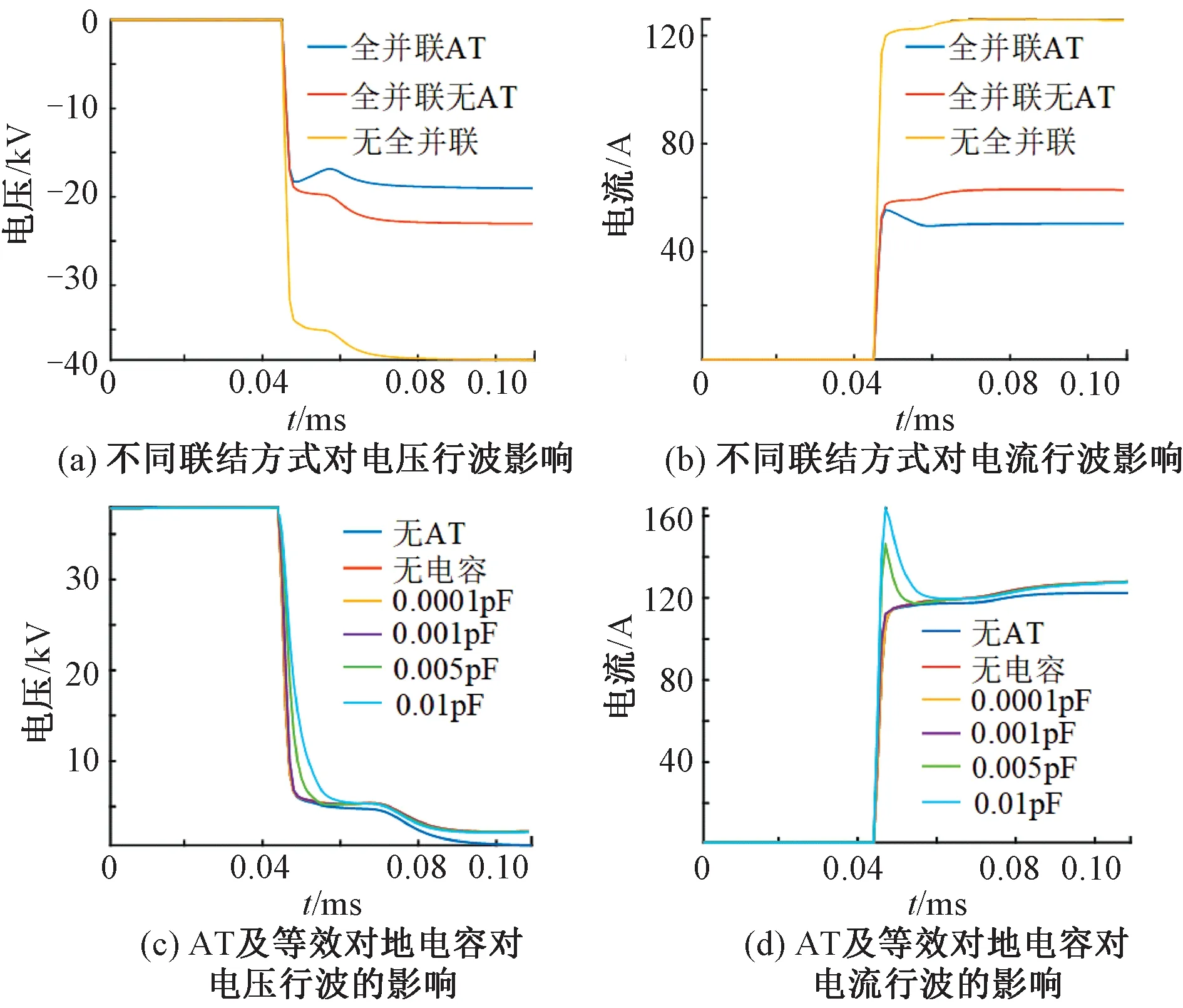
图2 全并联AT对行波波头的影响

从图2(a)、图2(b)可知，全并联AT连接方式对行波的影响主要是降低了其幅值，不管是电流还是电压行波幅值都降到初始行波的0.5倍左右。从图2(c)可以看出，AT自耦变压器对电压行波影响较小，当考虑AT所设备对地电容作用时，并联电容增大会使电压波形下降斜率降低。从图2(d)可以看出，AT自耦变压器对电流行波影响较小，可看成开路；当考虑AT所设备对地电容作用时，电容越大，会产生一个尖峰，对电流行波波头影响越大。从图2可以看出，当不考虑AT所设备对地电容作用时，AT自耦变压器本身对行波传播没有影响，可看成开路。

1.3 行波传播路径分析

以T-N短路为例进行分析，T-N短路时，由1.2节分析可知AT自耦变压器本身可看成开路，但行波会在其连接上下行形成的阻抗不连续点折反射，故障行波会在T1、T2上进行传播，故障行波传播路径如图1所示。全并联AT供电牵引网AT0端、AT2端可看成母线端连有2条线路，如图3(a)所示；AT1端可看成母线端连有4条线路，如图3(b)所示，初始故障行波到达AT0端T1、T2电流行波表达式为

图3 AT端接线示意

i1-AT0=-(1+βAT0)if(t-x/v)

( 2 )

i2-AT0=αAT0if(t-x/v)

( 3 )

式中：βAT0≈(nAT0-2)/nAT0=0；αAT0≈1；if(t)为故障起始电流行波；v为波速。

初始故障行波到达AT1端T1、T2电流行波表达式为

i1-AT1=(1+βAT1)if[t-(L1-x)/v]

( 4 )

( 5 )

式中：βAT1≈(nAT1-2)/nAT1=0.5；αAT1≈0.5。此时透射到L2区段T线上下行故障电流相似度较高。

初始故障行波到达AT2端T1、T2电流行波表达式为

i2-AT2=(1+βAT2-αAT2)i2-AT1(t-L2/v)

( 6 )

i1-AT2=(1+βAT2-αAT2)i2-AT1(t-L2/v)

( 7 )

式中：βAT2≈βAT0；αAT2≈αAT0。此时分区所AT2量测端T1、T2电流几乎为零。AT2端接线结构和AT0端接线结构相同，如图3(a)所示。

由图1和式( 2 )～式( 7 )可得：当发生T-N短路故障时，故障点位于L1区段，在牵引变电所端T线电流行波奇异性强；分区所AT2端的T1和T2电流波形相似度较高，并在AT2端互相抵消，使T1和T2电流行波奇异性较低，所以采用传统单端或双端测距会造成测距误差增大。对其他短路故障类型分析同上，可得出类似结论。

1.4 行波传播路径仿真验证

在EMTP中建立一条长30 km全并联AT牵引网线路的仿真模型，上下行线路采用基于频率相关参数的J.Marti线路模型。采样率设为1 MHz，过渡电阻为10 Ω，L1区段长为14 km，L2区段长为16 km，T-N短路点设在距牵引变电所5 km上行线处，短路时间为t=0.04 s。

由图4可知，故障点初始行波传播到AT1端有明显的折反射，牵引变电所端T线电流行波奇异性强，在L2区段的上下行T线电流重合度非常高，且AT2端T1、T2电流波形平缓，奇异性低，表明电流行波从AT1端透射到L2区段在AT2端几乎没有反射，与1.3节得出的结论一致。

图4 线路各点T线故障电流

牵引变电所端故障电流行波如图5(a)所示，模电流如图5(b)所示。从图5(a)可知，T-N短路时，行波主要在上下行接触线T上传播，因此将单独分析牵引变电所端T1和T2电流行波，波形图如图6所示，各行波传播路径见表3、表4。从图5(b)可知，模6电流行波奇异性最强，选择模6分量用于行波故障测距。

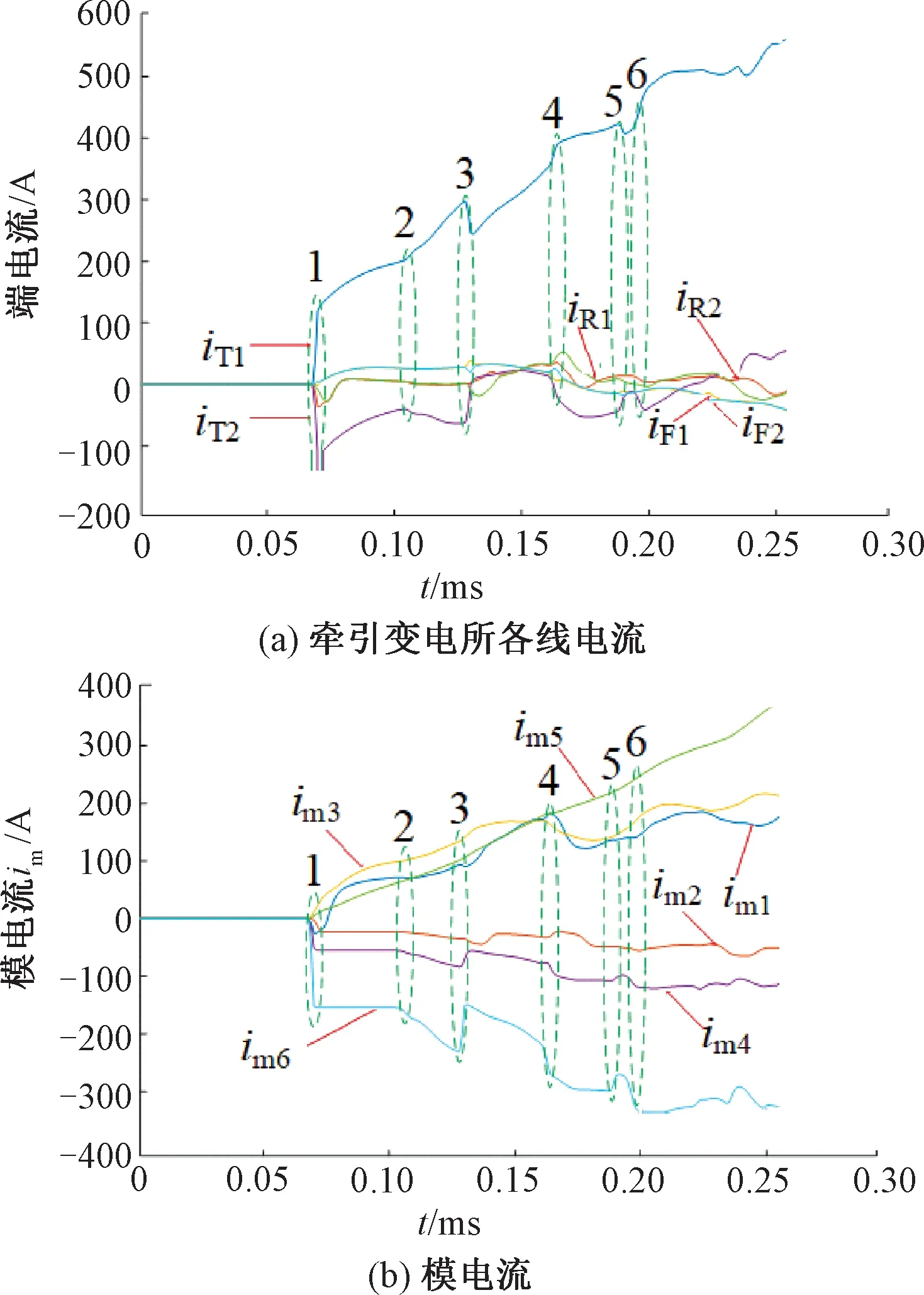
图5 牵引变电所电流行波和模电流

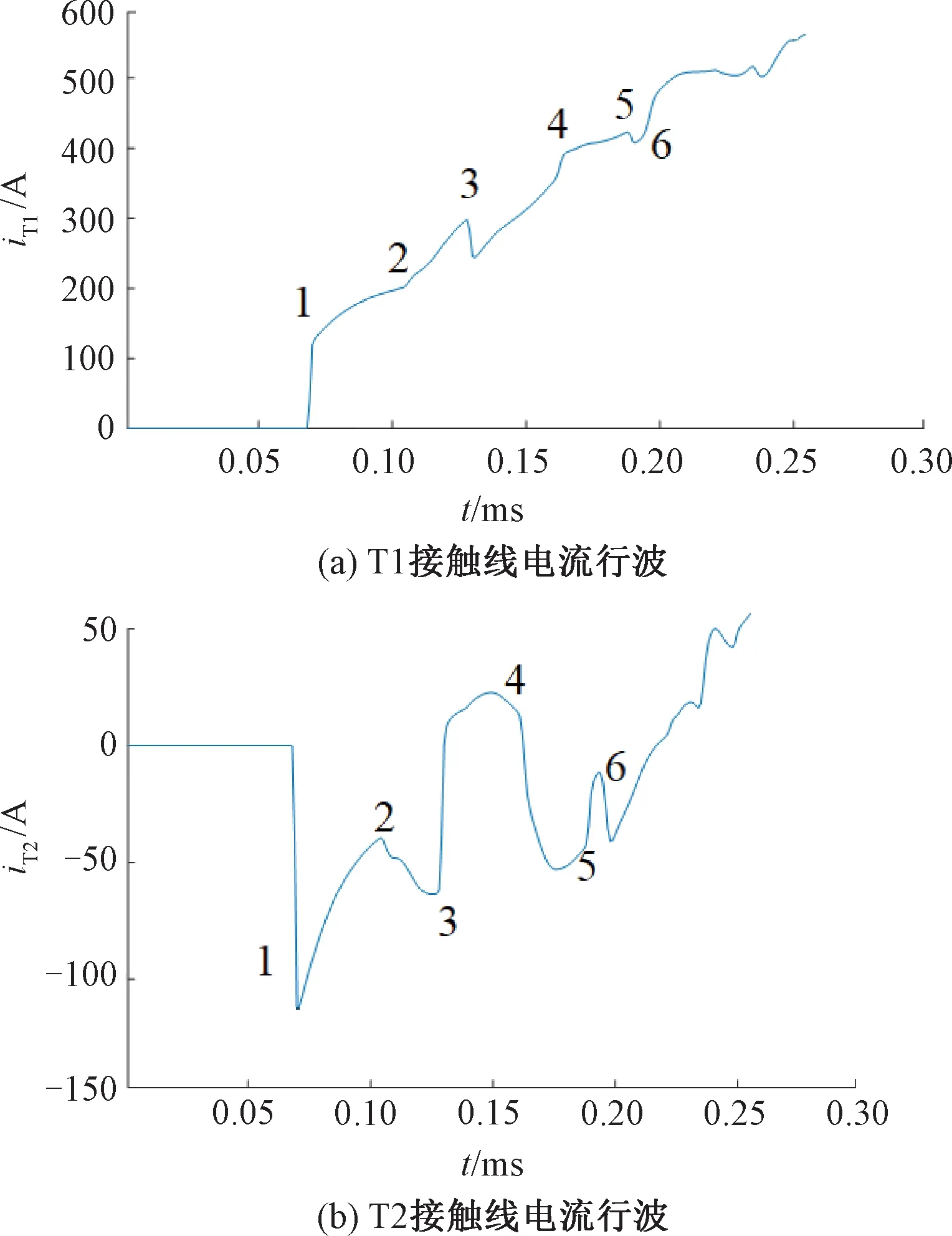
图6 牵引变电所端T1和T2接触线电流行波

表3 T1接触线电流行波中各个行波传播路径

表4 T2接触线电流行波中各个行波传播路径

从图6和表3、表4可知，波头2为故障点反射波，波形平缓，很难检测其奇异性；波头3奇异性强，是AT1端反射波。T1线上波头2与波头3的表达式为

i2=-(1+βAT0)βAT0βFif(t-3x/v)≈0

( 8 )

i3=αAT0αAT1if[t-(L1+x)/v]≈0.5if[t-(L1+x)/v]

( 9 )

式中：βAT0和αAT0分别为AT0端电流行波反射系数和折射系数；αAT0为AT1端电流行波折射系数；βF为故障点电流行波反射系数，βF=(ZC-RF)/(RF+ZC)。

从式( 8 )、式( 9 )可知，波头2奇异性低，波头3奇异性强。为消除噪声干扰，设定浮动幅值阈值，仿真中幅值阈值整定为模6分量初始行波幅值的5%[17]，如图7所示。

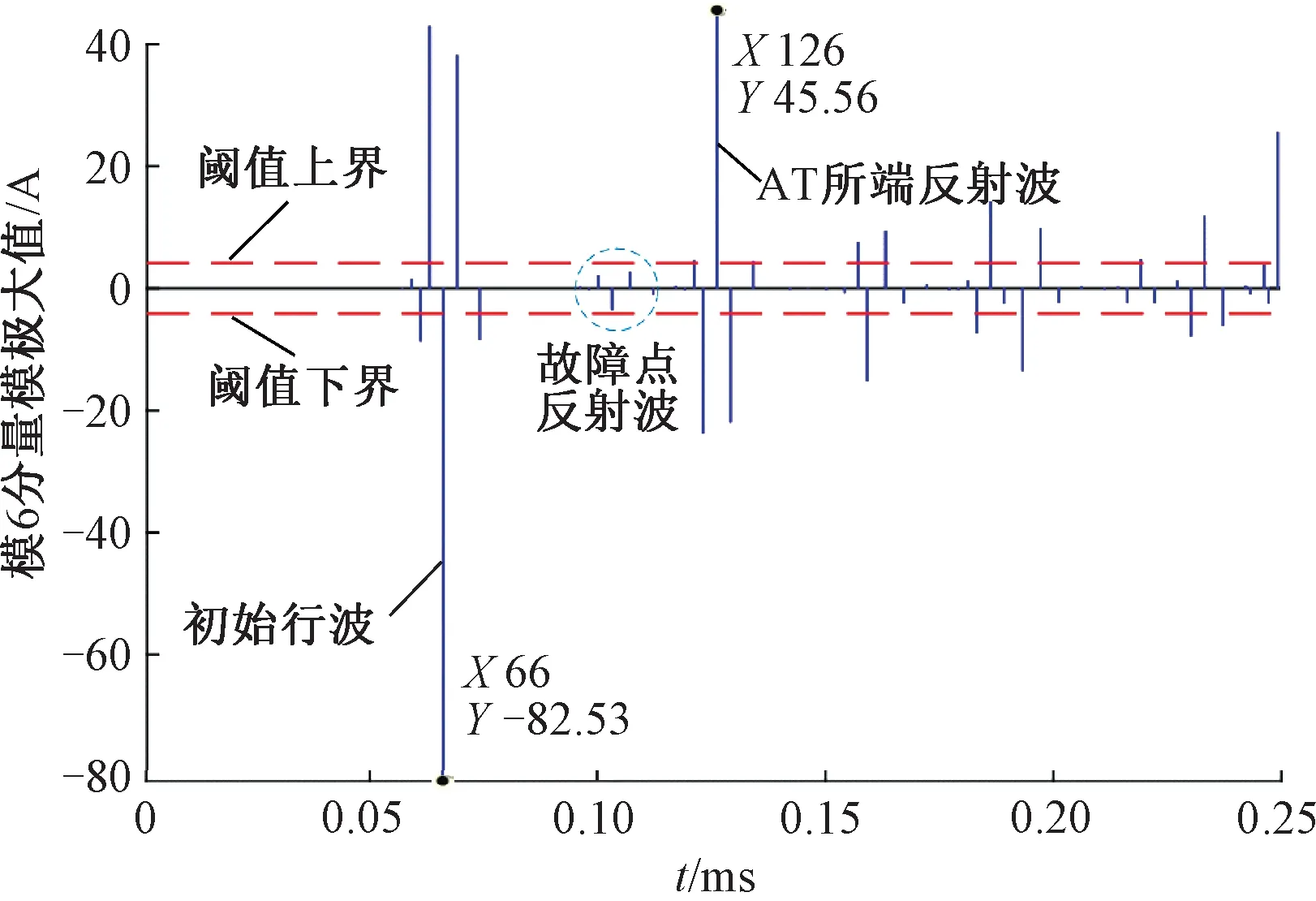
图7 模6分量小波变换模极大值

图7中的去噪阈值大于故障点的反射波，并根据式( 8 )、式( 9 )可知，采用单端测距法可直接忽略故障点反射波识别。故障距离为

x=L1-0.5×(t2-t1)vm6=5.016 km

(10)

通过上述分析，AT自耦变压器本身只有在考虑等效对地电容大于0.001 pF时电流行波会产生一个尖峰，随电容值越大尖峰越陡峭，而对电压行波几乎没有影响。其影响主要是AT连接上下行线路使得电压、电流行波在连接点的折反射系数为0.5。从牵引网首末两端的仿真波形可知：当故障点位于L1区段时，可利用首端电流行波故障点反射波与AT反射波幅值关系识别出AT反射波，从图(2)可得电压行波具有奇异性强，幅值大，几乎不受AT自耦变压器的影响的优点，再采用电压行波标定初始行波和AT反射波波到时刻t1和t2。当故障点位于在L2区段时，可利用末端电流行波故障点反射波与AT反射波幅值关系识别出AT反射波，再采用电压行波标定初始行波和AT反射波波到时刻t1和t2。由图(5)可知，模6分量具有奇异性明显且模速稳定的特性。

2 时频谱相似度识别故障点区段原理

为解决采用何种方法来判断选用首末哪个端的暂态行波用于单端测距的问题，可基于电流行波传播规律上寻找方法。根据1.3节可知，当故障点位于L1区段，分区所端T1与T2、F1与F2电流波形完全一致，而在牵引变电所端上下行电流波形不同；当故障点位于L2区段，牵引变电所端T1与T2、F1与F2电流波形相似度较高，而在分区所端上下行电流波形不同。两个波形的相似度可以依据其时频谱相似度判断[18]，为降低计算量，将时频谱等分划分为时频谱矩阵，通过计算牵引变电所端上下行电流行波时频谱相似度来判断故障点发生在哪个区段。

2.1 时频谱矩阵

牵引网发生短路接地故障时，产生的暂态电流是由不同频率分量构成的非线性、非平稳信号。将故障暂态电流分解成时频谱，使用小波包对故障暂态信号进行5层分解，得到25=32个频带，将每个频带时段划分成H等份，得到多个时频小块，定义频带m在时段n内时频小块的幅值为

(11)

(12)

时频谱矩阵E的具体构造方法：

(1)仿真采样频率设为1 MHz，对故障电流行波波形采集256个点，如图8(a)所示。使用小波包对暂态电流行波数据进行多尺度分解重构，分解层数为5，可得32个频带的小波包重构系数。

(2)每个频带按时间等分为32个时间段，得到32×32个时频小块，由式(9)计算某一频带每个时段的幅值，得到时频谱矩阵元素。即可得到故障信号的三维时频谱图，如图8(b)所示。

图8 故障信号及其时频谱

2.2 时频谱相似度识别方法

基于数字图像处理中相似度识别的思路，设Ea、Eb分别为2条上下行故障暂态电流波形的时频谱矩阵，则这2条线路的故障暂态电流波形的相似程度可描述[19]为

(13)

式中：M为频带数；N为时段数。文中M、N均取为32。将式(13)展开为

(14)

式中：第1项和第3项分别是变电所端2条不同线路小波包时频谱矩阵元素的平方和；第2项为2条不同线路之间的互相关度，随2条线路波形相似度的变化而变化。

对两条已知电流波形进行相似度检测，式(14)中的第1项与第3项为定值，因此只对式(14)中的第2项相似度检测并做归一化处理[19]，可得时频谱相似度Sab，其表达式为

(15)

式中：|Sab|≤1。Sab越大，说明2条波形越相似,若Sab=1，说明这2条波形一致。

2.3 时频谱相似度故障点区段判据

2.4 故障行波测距流程图

时频谱相似度故障行波测距流程如图9所示。

图9 基于时频谱相似度全并联AT牵引网行波测距流程

对故障电流信号做小波包重构分解，分解层数为5，得32个频带，对重构后的每个频带系数进行32等分，构造成32×32的时频谱矩阵E，将E看做是数字图像的像素矩阵，求出上下行暂态故障电流之间的时频谱相似度矩阵S。判别故障区段，如故障发生在L1区段时，使用牵引变电所端故障电流、电压行波进行单端测距；如故障发生在L2区段时，使用分区所端故障电流、电压行波进行单端测距。最终达到故障测距目的。

3 仿真验证

为验证基于时频谱相似度全并联AT牵引网行波测距方法的准确性，分别对距离牵引变电所不同距离发生不同故障情况进行仿真，按图9行波故障测距流程图测距，取模6电流、电压分量进行db4小波变换，波速取表2中的模6波速vm6=2.977 899×105km/s，故障区段判断见表5，故障测距结果见表6。

从表5可知利用时频谱矩阵可以准确判断故障区段，从表6可以看出在不同故障距离、不同故障类型、不同过渡电阻测距误差均小129 m。

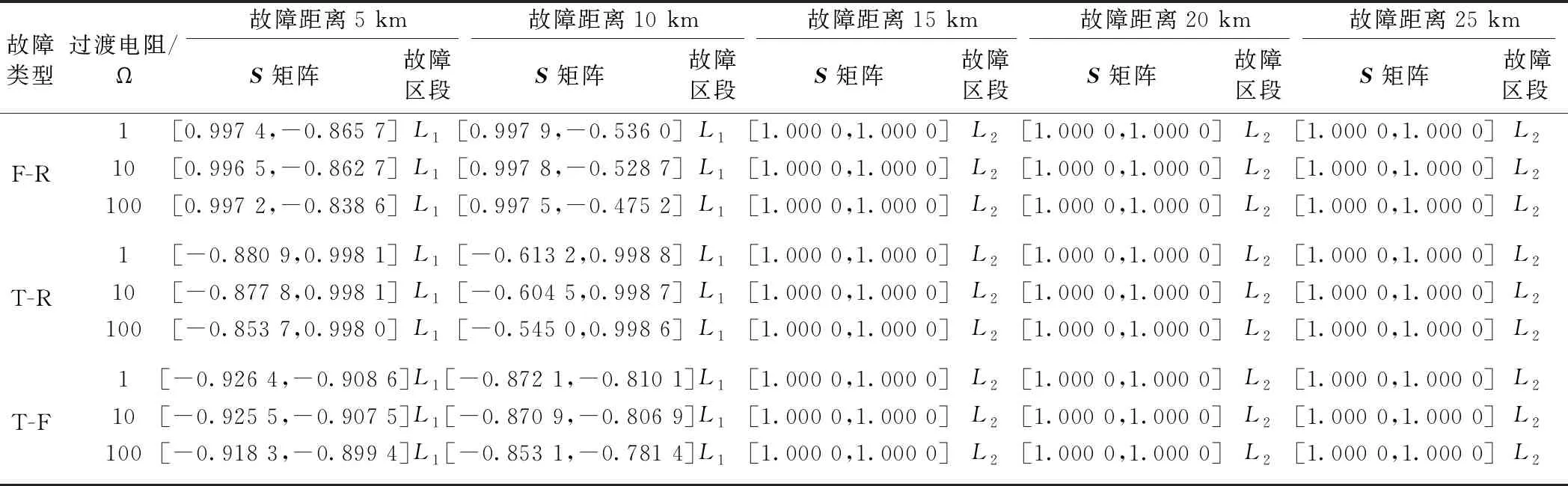
表5 故障区段判别

表6 故障测距结果

4 现场验证

4.1 现场装置测距结果

表7为2019年10月24日昌赣赣县北牵引变电所接触网短路试验故障测距结果，现场测距装置是基于“吸上电流比原理”制造，共进行了8次全并联AT运行方式下的各种短路试验，故障测距结果见表7，其误差最低为-99 m，误差最高达-1 209 m。

表7 昌赣赣县北供电臂“吸上电流比”现场测距结果

4.2 实测数据分析

昌赣赣县北接触网短路实测数据采样率为2 MHz，录波文件以COMTRADE格式保存，只有变电所端数据。

牵引网运行方式为全并联AT，供电臂接触网线路全长25.863 km，L1区段14.337 km，L2区段11.526 km，牵引变电所距上网点2.516 km，故障点1距变电所中心里程13.16 km，T1线电压波形如图10所示，故障点2距变电所中心里程27.089 km。实测结果见表8。

表8 昌赣赣县北接触网短路实测数据验证结果

将仿真结果与昌赣赣县北供电臂“吸上电流比”现场测距结果进行比对，并使用实测数据验证，本文提出的基于时频谱相似度全并联AT牵引网行波测距方法具有较高精度。

5 结论

(1)通过对故障发生时全并联AT牵引网首末两端的电流行波波形分析可得：当故障点位于L1区段时，首端暂态电流行波的奇异性远大于末端，更有利于被检测标定；当故障点位于L2区段时，具有相反的结果。由于全并联AT牵引网的特殊结构，故障点反射波幅值小于去噪阈值，从电流行波幅值关系可以识别反射波。电压行波具有奇异性强、幅值大、几乎不受AT自耦变压器的影响的优点，更有利于准确标定波到时刻。

(2)计算首端上下行电流暂态波形之间的时频谱相似度矩阵来选择首末哪个端的电流、电压行波用于单端测距，并经过仿真和实测数据验证了其有效性。

(3)在上述分析基础上，提出基于时频谱相似度全并联AT牵引网行波测距方法，提高了检测和标定波头的准确性，同时不需要双端数据对时，测距误差均在150 m范围之内，测距结果不受过渡电阻、短路类型等的影响，且与基于“吸上电流比”现场测距结果相比具有误差较小的优点。