基于轨迹数据的干线绿波协调控制效果评价

魏向达, 刘小明, 董路熙, 尚春琳

(北方工业大学 城市道路交通智能控制技术北京市重点实验室, 北京 100144)

0 引 言

城市干线绿波协调控制作为一种缓解城市交通拥堵的控制方法, 其相关研究多集中于控制模型的优化, 如：常玉林等[1]分析了绿波带速度、周期以及相位差等指标, 提出了一种双向绿波信号的改进图解法; 黄慧琼等[2]通过分析交叉口间距与车辆排队消散时间, 提出了一种干线绿波协调公共周期与相位差的优化方法; 于德新等[3]基于线性规划模型, 提出了一种干线协调控制优化方法, 实现了对MULTIBAND模型中绿波带形式的优化; 荆彬彬等[4]从车队实际行驶速度波动性出发, 以双向绿波带宽之和最大以及速度波动百分比之和最大为一、二级目标, 提出了一种绿波协调控制目标规划模型; 卢凯等[5]针对不同绿灯终点型绿波带设计, 构建了一种双向绿波协调数解法; 李永强等[6]针对绿波控制开环控制问题, 以最大绿波带宽为优化目标, 提出了一种数据驱动的交通响应绿波协调控制模型; Ma等[7]将自适应机制引入绿波控制, 以绿波带宽最大和延误最小为目标, 提出了一种基于自适应人工鱼群算法的绿波控制系统优化方法。上述算法研究重点侧重于算法优化, 不同算法模型在迁移到实际干线协调路段时算法适应性可能存在一定差异。因此, 对不同干线绿波协调控制效果评价研究有助于增强算法的鲁棒性, 提升干线绿波控制方案实际应用效果。

在绿波协调控制效果的评价方面, 卓曦等[8]从绿波系统效率与安全指标出发提出了一种绿波协调控制系统灰色关联评价方法; 施俊庆等[9]利用仿真软件对双向绿波控制效果进行了评价; 林清韩等[10]将绿波交通特有参数与传统指标相结合, 同时考虑次干道通行效率, 利用灰色关联分析法对绿波协调系统控制效果进行了评价; 卢凯等[11]通过计算行驶速度和绿波带宽之间的关系, 利用集对分析法对不同绿波控制方案进行评价。

从上述研究可以看出, 适用于不同干线绿波协调控制效果评价对比的方法较为缺乏, 且部分方法所使用的绿波协调控制效果评价指标较难获取。基于此, 本文以车辆轨迹数据为基础, 统计了车辆行驶OD矩阵表, 协同考虑车辆连续通过交叉口数与停车次数, 构建了干线绿波协调控制评价方法, 在保证评价方法简便可操作的基础上实现了对不同绿波控制方案的评价。

1 绿波控制评价方法

1.1 数据处理

目前，由于各种检测器与终端设备的应用使得对车辆数据的获取变得更加轻松、便捷, 丰富的数据使得对于交通控制的研究可以更加深入, 但若检测器损坏或数据传输过程中数据丢失, 则往往需要对车辆轨迹原始数据进行预处理以便获得有效数据。车辆轨迹原始数据信息主要包括: 车辆ID、时间戳、车辆经纬度、车辆速度。车辆轨迹信息数据结构如表1所示。

表1 车辆轨迹信息数据结构

本文所研究的车辆轨迹为干线绿波内的车辆行驶信息, 通过对比车辆经纬度信息与干线绿波内路段边界信息选择出目标区域内的车辆轨迹信息。路段轨迹点坐标为L(lon,lat), 绿波协调路段边界点为L1(lon1,lat1)、L2(lon2,lat2)、L3(lon3,lat3)、L4(lon4,lat4), 其中目标边界除了包括绿波协调路段外，还应包括协调交叉口中非协调方向路段, 以便对后续车辆行驶轨迹时对于轨迹的判断更加准确。A为边界点围成的区域, 当L∈A时则为有效点, 对A区域外的点进行数据清除, 有效数据区域如图1所示。

图1 有效数据区域示意图

为便于数据处理与统计, 在完成有效数据获取后将时间戳转换为标准时间, 进而对数据中存在的重复数据与缺失数据进行处理。以车辆ID作为检索基础, 在目标时间段内对车辆重复信息进行清理, 缺失数据通过同一车辆ID的数据进行关键数据的补全与无关数据的清除。在完成数据处理后，通过对车辆轨迹信息与实际地图信息的匹配, 利用车辆ID为基本单元生成车辆轨迹时空图(图2), 再用车辆的轨迹数据进行车辆OD数据统计。

图2 车辆轨迹时空示意图

1.2 车辆OD矩阵

OD矩阵是描述交通网络中所有起点到终点之间在一定时间范围内交通流量的表格, 反映了某个城市或区域的基本交通需求[12]。OD矩阵在交通规划研究中占有极其重要的地位, 能揭示出城市交通症结的原因、交通需求与土地利用、经济活动的规律[13]。本文将干线绿波协调路段编号作为OD矩阵中的起点与终点。

在完成原始数据处理后, 将所测绿波协调控制路段位置信息与车辆轨迹数据进行匹配, 获得每辆车的行驶轨迹与速度, 以便基于绿波协调路段内车辆轨迹统计车辆OD数据。定义：在绿波协调控制路段内连续通过2个及以上交叉口的车辆为有效绿波协调车辆；绿波协调路段内车辆OD出行中出发点为车辆初始进入绿波协调交叉口前路段编号, 其中车辆停驶后再启动算作新出发点；目的地为车辆驶离干线绿波路段编号或由于延误而在干线绿波内开始排队路段编号, 即在干线绿波协调控制中车辆一次出行可能存在多个OD出行。由于本文提出的评价方法对于双向绿波与单向绿波计算方法相同, 现用单向绿波交通进行例证说明。绿波交通干线示意图如图3所示, 其中Ci表示干线绿波中第i个交叉口,Li表示干线绿波中第i个路段。

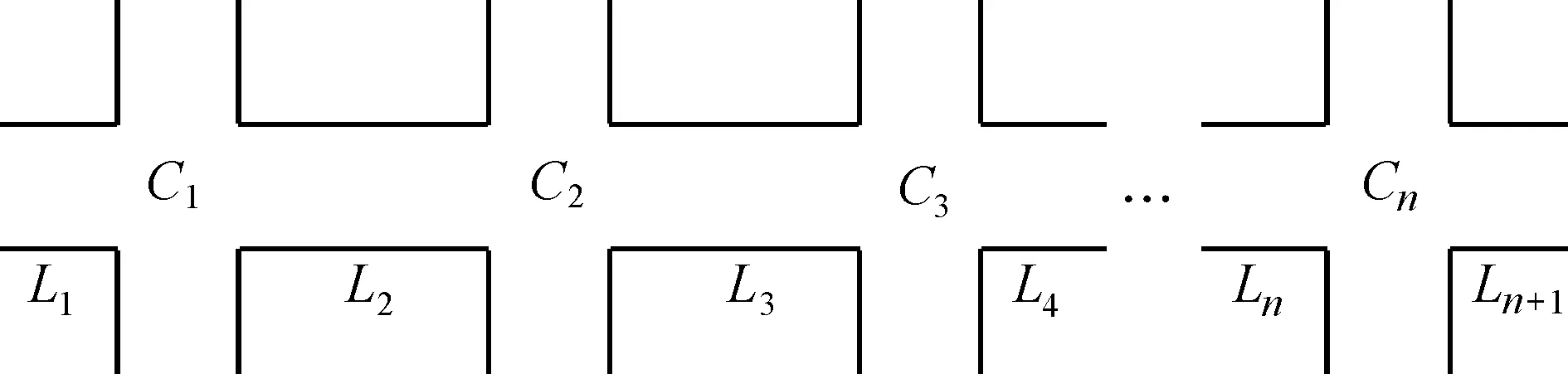
图3 绿波交通干线示意图

根据车辆轨迹数据统计干线绿波车辆通行情况, 记录车辆OD出行表, 车辆OD矩阵统计流程图如图4所示，详细步骤如下:

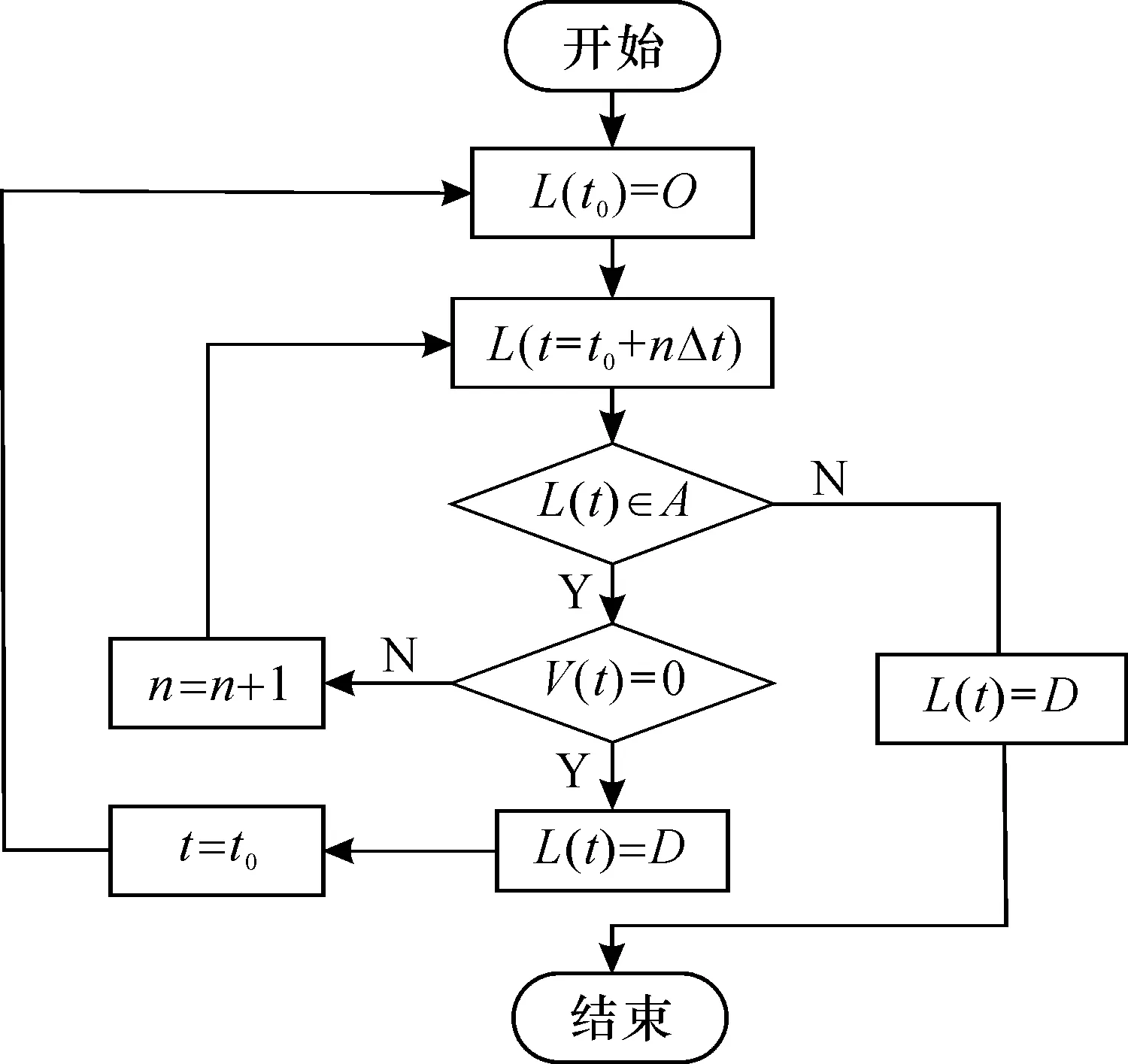
图4 车辆OD数据统计流程图

Step 1: 检测进入干线绿波协调控制路段内车辆初始时间t0位于路段位置信息起点O。

Step 2: 判断车辆下一检测时间间隔Δt的t=t0+nΔt(n∈N+)时刻的位置L(t)是否属于干线绿波内相关路段A: 若L(t)∉A, 则判定t时刻为车辆的终点，完成车辆的OD数据统计; 若L(t)∈A, 则执行Step 3。

Step 3: 对车辆在t时刻速度Vi(t)进行判定: 若Vi(t)≠0, 则判定车辆未停止运行, 则令n=n+1,返回Step 2; 若Vi(t)=0, 则判定车辆停止运行,t时刻为车辆的终点完成车辆的OD数据统计, 并执行Step 4。

Step 4: 令t=t0, 返回Step 1对车辆进行下一次OD数据统计。

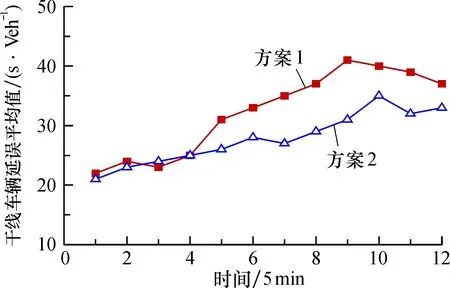
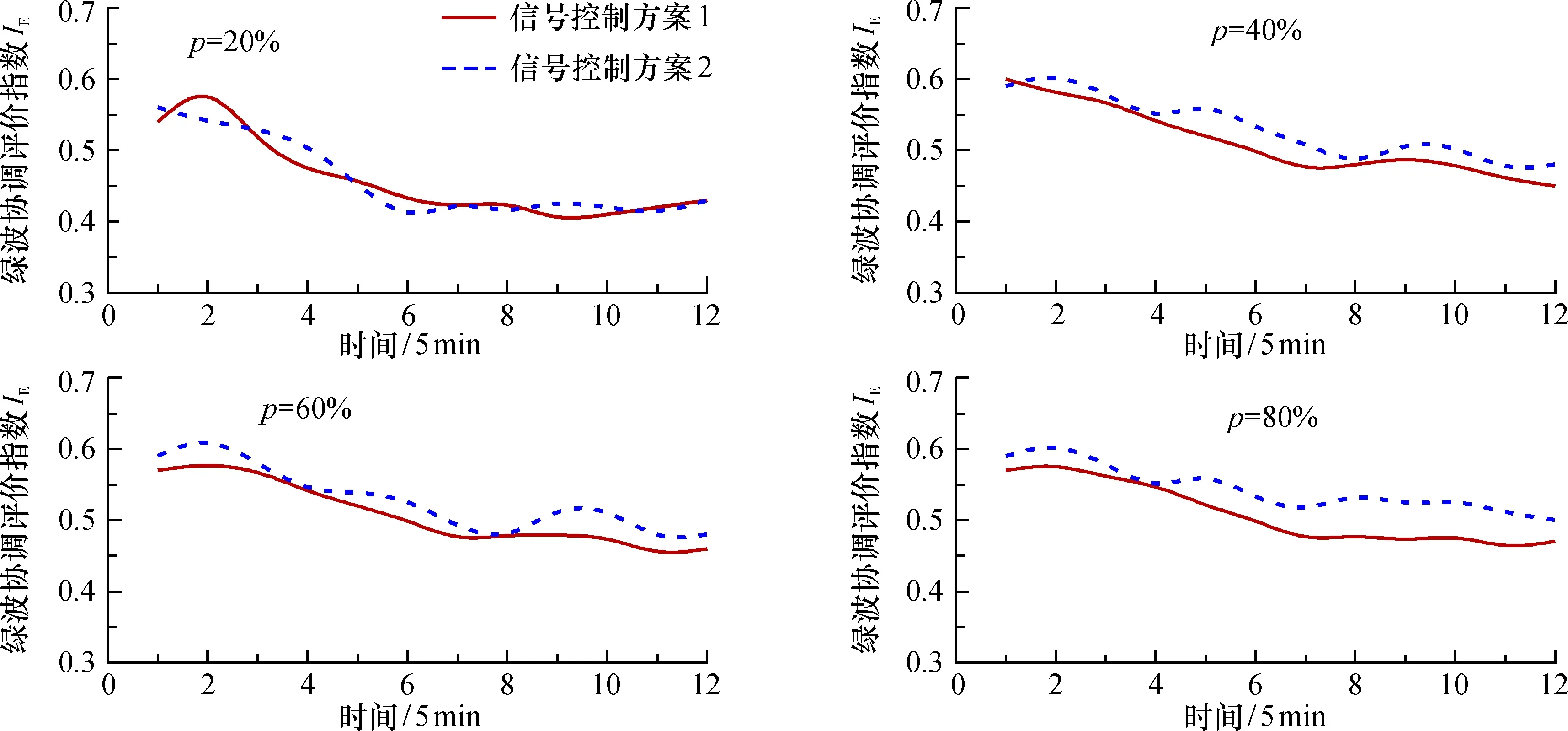
依照OD矩阵数据统计流程遍历绿波协调控制路段车辆, 干线绿波车辆OD矩阵如表2所示，其中：i、j分别表示进入以及驶离绿波交通路段编号, 1

表2 车辆OD矩阵

定义车辆OD矩阵中i、j满足j-i<2时车辆为未进入干线绿波协调车辆, 即车辆连续通过2个路口才定义为进入干线绿波协调; 定义车辆OD矩阵中i、j满足j-i≥2时车辆为进入干线绿波协调车辆。

此外, 统计车辆从i路段进入绿波协调路段至从j路段驶离的车辆数Ni,j′, 构建传统车辆OD矩阵, 用于计算理想通行效率值。

1.3 绿波评价指数设计

按上述车辆OD矩阵进行绿波评价指数设计。以交通评价作为交通控制的基础, 其从指标选取，到权重确定，再到目标函数确定，具有整套的评判流程。城市干线绿波协调控制作为一种特殊的交通控制方法, 在对比不同控制方案效果评价时, 由于干线绿波协调控制内交通状态会造成车辆行驶速度与设计车速产生偏离, 而一般的交通评价方法是对于交通状态的评价, 其评价结果的好坏与交通状态有直接关系, 因此难以进行不同干线绿波协调控制方案的评价。而对于绿波干线协调来说, 其本质上应将干线协调前后状态提升程度作为评判依据。综上, 本文从干线绿波协调控制实际效果出发, 构建干线绿波协调控制效果评价方法。

干线绿波协调设计目的是尽量使更多车辆在设计车速行驶下在每个路口都遇到绿灯, 从而保证干线绿波能够承载更多交通量。对于干线协调车辆而言, 车辆连续通过交叉口数目将极大影响驾驶员对于干线绿波控制效果的整体感受。在一定的交通状态下，车辆连续通过交叉口车辆数目越多等价于车辆在干线绿波内平均行驶时间越短，但由于车辆一次出行可能存在不同连续通过交叉口数组合, 仅以实际车辆连续通过交叉口数目进行评价会影响评价结果的准确性。为了克服交通状态随机性对评价结果造成的波动, 在实际车辆连续通过交叉口数目上引入了理想车辆连续通过交叉口数, 车辆一次出行产生的不同OD出行, 分别根据其理想车辆连续通过交叉口数计算实际绿波协调对于理想状态的近似程度。此外, 由于实际绿波协调运行中未进入绿波干线协调车辆数量存在波动性, 其数值大小会干扰绿波协调实际运行状况, 故在干线绿波评价时需对其进行剔除。

综上, 本文设计了绿波实际通行效率值、绿波理想通行效率值、绿波通行扰动值, 进而综合计算绿波协调评价指数, 最终对城市干线绿波协调控制进行评价。评价流程图如图5所示。

图5 评价流程图

基于车辆OD矩阵统计数据计算相关指标如下:

1)绿波实际通行效率值(IR)。对于进入干线绿波协调车辆计算绿波实际通行效率值IR, 其指标大小表示车辆在绿波协调控制方案实际运行状态, 其物理意义为从不同路段进入绿波协调控制路段的车辆数与其相应实际连续通过交叉口数的乘积。对于单车而言,IR代表干线绿波在实际状态下的车辆客观打分, 打分值为单车实际连续通过交叉口数; 对于全部车辆而言,IR的计算公式为

(1)

2)绿波理想通行效率值(II)。对于进入绿波协调车辆, 理想情况下，车辆从进入绿波协调路段遇到的首个绿灯交叉口开始一直到驶离干线绿波路段内所经过的各个路口均为绿灯。结合车辆OD矩阵数据与理想连续通过交叉口数计算绿波理想通行效率值II, 其表示绿波控制效果的理想运行状态, 实际含义为所有OD出行中各交叉口驶入车辆数与其在绿波协调干线内行驶时理想状态下可连续通过交叉口数的乘积。对于单车而言，II代表干线绿波在理想状态的车辆客观打分, 打分值为单车在绿波协调路段行驶内理想连续通过交叉口数; 对于全部车辆而言,II的计算公式为

(2)

3)绿波通行扰动值(ID)。对于未进入干线绿波协调的车辆, 其数量会对干线协调控制效果造成影响, 在计算绿波理想通行效率值时,Ni值将未进行绿波协调车辆纳入统计范围, 同时, 当存在大量车辆未进行干线绿波协调控制等极端场景时要保证评价结果的稳定性, 就必须将未进行协调车辆从其中剔除。此外, 不同绿波协调方案在实际应用中, 控制场景具有不可重复性。为消除上述因素对评价结果的影响, 定义了绿波通行扰动值ID, 其实际意义为绿波协调控制路段内未进入绿波交通的车辆数与连续通过的交叉口数。对于单车而言，ID代表未进入绿波协调车辆客观打分, 由于对象是未进入干线绿波协调车辆, 其打分值均定义为1; 对于全部车辆而言,ID计算公式为

(3)

4)绿波协调评价指数(IE)。对于绿波协调评价是基于实际通行效率值, 在考虑干线绿波扰动值大小前提下, 计算其相较于绿波理想通行状态的近似程度。绿波协调评价指数IE计算公式为

IE=IR/(II-ID)。

(4)

对于不同绿波协调控制效果评价, 评价结果首先由绿波协调评价指数IE确定,IE值越大，则表明绿波控制效果越佳; 同时，当|IE1-IE2|≤ε(ε为任意无穷小)时, 则比较IR值,IR值越大，则表示绿波控制效果越佳; 而|IR1-IR2|≤ε时, 进一步对比ID值,ID值越大，则表示绿波控制效果越佳。

2 仿真验证

以文献[14]中干线绿波协调交叉口基本数据为基础, 用VISSIM仿真软件构建干线绿波协调实验, 仿真路网如图6所示。干线长度为0.94 km, 其中包括4个T型交叉口, 交叉口从下至上分别为交叉口1～4, 交叉口间距分别为234、281、166 m,各交叉口流量流向如表3所示,仿真持续时间为1 h。

表3 干线流量调查统计[14]

图6 仿真路网结构示意图

文献[14]中通过实际调研, 拟定了2种绿波干线协调控制方案, 其分别为将整个干线绿波协调划分为多个子区下的绿波协调控制方案与常规4个交叉口共周期的干线绿波协调控制方法。第1种信号控制方案中前两交叉口公共周期为132 s, 后两交叉口公共周期为162 s; 第2种控制方案中公共周期均为170 s。详细配时如表4所示。

表4 干线信号配时方案对比[14]

用VISSIM仿真建模可以模拟实际干线绿波协调的运行状态, 在保证安全性的同时还可以方便对不同绿波协调控制方案进行模拟。VISSIM不仅具有丰富的评价功能, 可以获取有效的交通评价参数, 还可提供丰富的COM接口支持二次开发。

3 结果分析

VISSIM仿真软件可以输出相关延误、停车次数等交通评价数据, 其结果具有一定可信性。为使评价结果更加可信, 利用多次仿真获得路网的干线绿波协调车辆延误值作为本文评价方法的参照进行一致性检验。以5 min为单位时长, 在仿真时长内分别统计两个方案的车辆延误情况, 结果如图7所示。在大部分仿真时间里，绿波控制方案2控制效果优于方案1。在仿真初始运行阶段，由于仿真车辆仍未进入中心交叉口, 干线绿波内车辆未达到预期交通量, 此时边界交叉口信号控制方案对与整体绿波协调控制效果的评价起到了关键作用, 可见仿真软件并不能真实反映控制方案的情况。总体上，去除由于仿真软件造成的数据偏差, 两方案控制效果都随着路网交通状态的稳定而趋于平稳, 同时干线绿波的车辆延误状况在一段时间增长态势后呈现稳定状态, 方案2与方案1相比车辆延误降低了18.15%, 其控制效果体现出明显的优越性。

图7 不同绿波控制方案车辆延误对比

此外, 同样以5 min为单位进行车辆OD矩阵表的统计并计算两方案的协调指数, 结果如图8所示。控制方案2同样优于方案1, 其VISSIM仿真评价数据得出的结论具有一致性。值得注意的是, 相较于VISSIM仿真评价结果在初始时产生了结果偏差, 本文所提出的绿波协调控制效果评价方法在交通状态变化下表现出了一定的稳定性。

图8 不同信号控制方案的绿波协调评价指数

对于实际干线绿波内车辆轨迹数据并不能完全获取问题, 利用MATLAB联合VISSIM二次开发, 通过在不同轨迹数据采集车辆渗透率p下的评价结果分析, 尽可能地模拟实际绿波干线内车辆数据特征, 进而对评价方法的鲁棒性进行验证。不同渗透率下绿波协调评价结果分析如图9所示。整体而言,绿波协调信号控制方案2优于方案1,其结果与采用延误作为评价结果具有一致性。同时，随着轨迹数据采集车辆渗透率的降低, 绿波协调信号控制方案2相较于方案1的优越性逐步降低。当渗透率降低到20%时, 信号控制方案2的优越性难以被有效刻画, 究其原因在于, 当渗透率降低到一定程度时, 干线绿波内随机性被放大, 对于绿波协调评价指数IE不稳定归结于实际绿波通行效率值IR,IR在低渗透率时会产生较大的波动性, 故影响最后方案评价结果。但总体看来, 在保证轨迹数据采集车辆一定渗透率下, 该评价方法具备实际可行性。

图9 不同渗透率对绿波协调评价结果影响

4 结 论

本文提出了一种基于轨迹数据的干线绿波协调控制效果评价方法, 从绿波协调实际运行状况出发, 面对不同绿波干线控制效果对比的困难, 通过定义车辆OD矩阵来记录干线绿波协调车辆运行状况, 同时结合绿波交通特性利用连续通过交叉口数为车辆进行打分, 并以此为基础计算干线绿波实际运行状态相较于理想状态的近似程度, 实现了不同干线绿波协调控制效果评价。仿真结果表明, 所提出的评价方法可以实现对不同绿波控制方案的有效评价，且在一定渗透率下本评价方法也具备可行性，但是由于受仿真模型限制, 对于更多交通状态下干线绿波协调控制效果评价, 以及在不同绿波协调交叉口数与交叉口类型下的绿波控制效果评价有待进一步研究。