基于LMD改进GPR优化的网络流量预测

智 春, 杨呈永, 崔建明

(桂林理工大学 a.信息科学与工程学院; b.现代教育技术中心; c.继续教育学院, 广西 桂林 541006)

0 引 言

大数据背景下, 用户对网络的要求越来越高, 网络运行负荷和状态直接影响到上网体验。网络流量作为网络负荷状态的重要参数, 其未来时间序列的网络流量状态将对用户上网产生重要影响。

针对网络流量的预测: Tian等[1]提出了一种基于改进的自由搜索算法优化最小二乘支持向量机的网络流量预测方法, 该方法具有较好的预测效果, 预测误差较小, 但增加了算法的时间复杂度; 龙震岳等[2]提出一种组合小波包分解(WPD)和灰狼横纵多维混沌寻优算法(CCGWO)优化Elman神经网络的短期网络流量预测模型(WPD-CCGWO-ELMAN), 组合模型具有较好的预测精度和鲁棒性, 但灰狼横纵多维混沌寻优算法在寻找全局最优时所用时间太长, 计算量大; 此外, 还有基于ABC+AFS-LSSVM的网络流量预测模型[3]、基于IWO-ESN的网络流量研究[4]、混沌理论[5]等方法应用于网络预测。同时, 优化参数的选择对模型的预测效果有着重要的影响, 常见的优化算法有粒子群、蚁狮、差分等[6-8]优化算法。为解决行车路径规划问题, 文献[9]提出一种混合遗传蚁群算法来优化路径的分配, 提高计算效率, 能够准确的满足路网综合要求。为解决迭代后期出现的早熟收敛, 文献[10]提出一种自适应混合粒子群优化算法, 使用差分策略更新粒子的随机位置, 使得粒子逼近最优位置；文献[11]利用模拟退火提高粒子群算法的全局性, 优化BP神经网络的权值和阈值, 对实际采集的网络流量时间序列进行建模, 具有更高的预测精度和良好的自适应性。

考虑到网络流量的复杂性, 蚁群算法优化参数对预测模型容易陷入局部最优, 本文提出了一种改进蚁群算法, 来提高算法的搜索能力。首先通过局部均值分解(LMD)将网络流量分成多个简单的相关序列, 再使用高斯过程回归(GPR)对多个相关序列进行建模分析，最后在蚁群中提出引入视线角度参数, 来扩宽蚂蚁的视线范围, 降低了搜索的随机性, 同时, 利用莱维飞行机制更新蚂蚁的步长, 使算法达到全局最优。

1 高斯过程回归原理

针对网络流量在高斯过程回归的应用作了许多研究: 李松等[12]提出将高斯过程混合模型(GPM)应用于网络流量的多模态预测, 对样本进行归一化和重构, 采用分类迭代学习算法, 利用后验概率最大化和似然函数对模型参数进行统计，再对统计的结果进行学习, 得到最适合模型的参数值，为网络管理者分配资源提供参考；Bayati等[13]设计了一种考虑包括周期性、非线性和非平稳性等不同流量特征的有效预测模型, 通过为时间序列预测提出一个学习者集合, 该集合考虑了个体学习者的准确性以及学习结果的多样性，每个学习者都通过在特征空间中寻找最优的精度多样性平衡来优化，这种分而治之的方法避免了具有许多局部最优的复杂目标函数；Sun等[14]提出无限变分近似高斯过程用于流量的预测, 和Dirichlet结合根据数自动确定, 克服了单高斯过程模型计算复杂的不足, 验证了该方法的有效性。

在数学定义上, 高斯分布是由均值和方差决定的。因此, 高斯过程模型的关键是对均值和方差的确定。给定一个数据集D{X,Y}, 将其根据具体的情况划分为训练集合{Xt,Yt}和测试集合{Xp,Yp}, 一般训练集大小为数据的80%或70%, 测试集为20%或30%。假设噪声服从0均值的高斯分布, 预测模型如下

y=f(x)+v；

(1)

(2)

cov(y*)=K(xp,xp)-K(xp,xt)[K(xt,xt)+

(3)

其中, cov(y*)是预测值的方差。

GPR的训练过程是利用核函数的映射将数据映射到高维空间。核函数选择径向基核函数, 其表达式形具体为

(4)

2 蚁群算法原理(ACO)

2.1 经典的蚁群算法

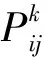
(5)

(6)

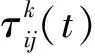
蚂蚁的信息素更新公式如下

(7)

其中:ρ为信息蒸发系数, 一般设置为[0.7,0.9]; 蚂蚁搜索范围为[-1,1]; 蚂蚁数量通常为[10,50]。

2.2 改进的蚁群算法(VACO)

经典蚁群算法在搜索时受到位置和速度的影响, 忽略了蚂蚁本身观察视线范围的因素。由于搜索路径的凹凸不平, 蚂蚁的视线角度对当前路径的搜索有一定的影响, 导致对局部搜索的不完整。同时, 由于搜索步长的因素, 造成蚁群算法容易陷入局部最优。本文一方面通过引入视线参数多方面控制蚂蚁的搜索位置, 避免了单一因素对蚂蚁位置的影响, 扩宽了蚂蚁移动的视线范围, 提高局部搜索能力; 另一方面通过莱维飞行更新步长, 避免陷入局部最优, 提高算法的全局效果。

改进的蚁群算法如下:

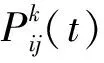
(8)

2)引入视角参数多变量控制蚂蚁搜索位置的更新：

(9)

(10)

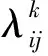
3)通过莱维飞行的跳跃性更新步长

(11)

其中: levy(λ)是随机搜索路径; ⨁是点乘;α为控制因子, 满足莱维分布

levy～u=t-λ, 1≤λ≤3。

(12)

由于莱维飞行计算复杂, 采用Mantegna算法计算步长s

(13)

(14)

通常β取为1.5。算法的基本流程:

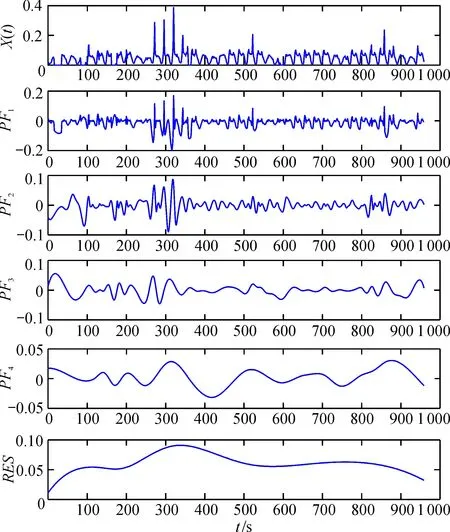
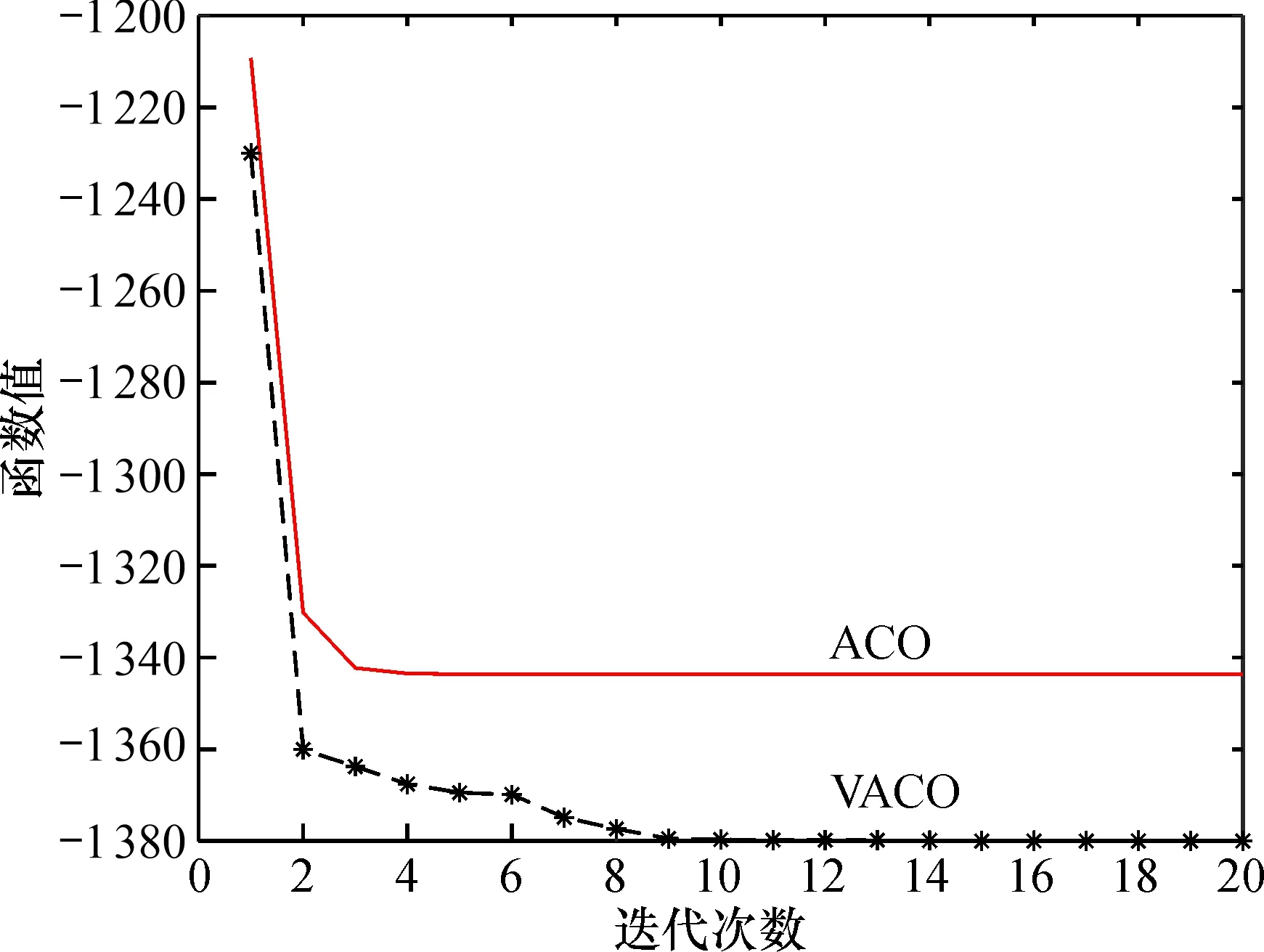
①设置初始参数, 包括蚂蚁的数量N、所在的位置x、移动的次数nT、视角参数sj和区间范围l等; ②对蚂蚁的个体极值和全局极值初始化; ③计算相应的转移概率, 如果P(i)

VACO算法流程如图1所示。

图1 VACO算法流程图

3 基于LMD改进蚁群优化的GPR网络流量预测

网络流量往往受到多种因素的影响,如上网时间、节假日高峰、地区网速、网络攻击等。Sun等[16]将单任务学习和多任务学习分别用于单链路和多链路的流量预测,同时将图像套索与神经网络结合来解决涉及多变量的问题,提高了预测的精度。在此,将网络流量看作一个复杂的非线性序列,基于将复杂问题分解成多个简单问题的数学思想, 提出使用局部均值分解(local mean decomposition,LMD)将网络流量分解成多个短相关序列,考虑到高斯过程回归能够很好地处理高维数、非线性的关系,并且具有容易实现、输出具有概率意义的特点,本文使用GPR对相关短序列进行建模分析,用改进的蚁群算法优化模型参数。预测模型结构如图2所示。

图2 本文算法结构图

4 实验设计和分析

4.1 实验数据和指标

通过收集某地区企业内部网络新闻热度的流量进行实验, 数据采集间隔为1 h, 提取其中960个数据进行仿真分析, 通过对前一个月访问产生的网络流量的建模来预测后10天的网络流量情况。网络流量的原始数据X(t)和LMD分解的PF1、PF2、PF3、PF4和RES序列如图3所示。

图3 原始数据和LMD分解图

为了验证各算法的预测效果, 本文通过计算预测值和实际值的平均绝对误差(MAE)、均方根误差(RMSE)和平均绝对百分误差(MAPE)来作为指标, 评价每个算法的预测效果:

(15)

(16)

(17)

4.2 实验对比和分析

采用MATLAB进行仿真实验, 针对研究问题, 将构造数据集的k设置为7, 蚂蚁数量为10, 迭代次数为30, 使用GPR对PF1、PF2、PF3、PF4和RES进行建模预测。

由图4a可看出, GPR对PF1突发点的预测效果并不理想; 从图4b—e可以看出，GPR对PF2、PF3、PF4和RES的预测效果较好。因此, 为了进一步提高网络流量的预测精度, 本文提出采用ACO优化GPR模型参数来预测PF1, 同时, 通过调整视线范围和莱维飞行机制的跳跃性来改进ACO的搜索情况。

图4 GPR对各分量突发点的预测

从图5可看出, VACO算法在初始时下降范围更大, 说明引入视线参数后, 蚂蚁具备了更广阔的视野, 找到了更好的搜索路径; ACO算法在迭代6次后趋向于稳定, 而VACO在迭代6次之后还在不断跳跃, 直到14次左右才趋向于稳定, 说明莱维飞行机制的随机步长提高了蚂蚁搜索的全局性, 能够找到更优的解。同时, 从图6和表1可以看出, VACO优化的GPR预测PF1更好地拟合了PF1的走向, 在MAE、RMSE、MAPE各方面, 相比GPR和ACO, VACO的误差都有所降低, 提高了对PF1的预测精度。仿真结果表明, VACO算法相比ACO而言, 局部搜索能力更强, 同时, 在一定程度上避免陷入局部最优; 随着迭代步数的增大, 蚁群算法将可能产生更多的跳跃性动作, 更加逼近最优解。

表1 各模型对PF1预测误差对比

图5 ACO和VACO的迭代轨迹

图6 VACO对PF1的预测结果

从图7对比可看出,经LMD分解,VACO优化GPR模型的预测较好地拟合了网络流量的走向,能够很好地预测突发点。从表2可看出, LMD-VACO-GPR在MAE、RMSE方面, 相比其GPR、LMD-GPR、ACO-GPR、VACO-GPR和VACO-GPR模型误差更低, 具有更好的预测效果。在MAPE方面, LMD-VACO-GPR相对较大, 这可能是由于LMD对网络流量序列的分解误差导致。经过对比分析, 说明基于LMD的改进蚁群优化的GPR预测方法是有效的, 具有更高的预测精度, 能够满足预测的需要。

图7 LMD-VACO-GPR的网络流量预测结果

表2 各模型的网络流量预测误差对比

5 结束语

为了能更好地提升网络用户的上网体验, 本文使用高斯过程回归对网络流量情况进行建模, 通过蚁群算法优化模型参数, 提出增加蚂蚁的视线角度参数扩宽了蚂蚁搜索的路径, 降低了随机性, 提高了局部搜索能力; 莱维飞行机制的跳跃性不断跳出局部最优, 提高了算法搜索的全局性。结果表明, 基于LMD的VACO优化的GPR算法提高了预测的准确性, 对维护网络安全具有重要的作用。下一步工作将寻找更好的特征分解方法, 使其网络流量能够彻底分解, 进而对其进行预测。