考虑变荷载影响的水下盾构隧道双层衬砌力学特性分析

2022-07-12龚振华梁敏飞

铁道标准设计 2022年7期

刘洋,龚振华,梁敏飞,何川

(1.西南交通大学交通隧道工程教育部重点实验室,成都 610031； 2.西南交通大学土木工程学院,成都 610031)

随着我国交通基础设施建设的不断发展，我国水下盾构隧道建设正面临越来越多大埋深、高水压的复杂问题，目前，常规单层管片衬砌结构可能无法满足安全性和耐久性要求。相对于单层管片衬砌而言，双层衬砌结构在补强、防火、防撞、抗沉降、防侵蚀、抗水压等方面更有优势。因此，双层衬砌结构越来越多地应用到水下盾构隧道建设中。

国内外针对盾构隧道双层衬砌的研究多集中在双层衬砌结构受力特性及计算分析方法方面。半谷[1]于1985年提出了用弹簧来模拟双层衬砌相互作用的模型，可模拟出层间压缩作用和剪切作用；崛地紀行等[2]对隧道二次衬砌圆管的轴向刚度进行研究，衬砌圆环间的接头也用弹簧来代替，该模型考虑了环间压缩刚度和剪切刚度； NASRI[3]和村上博智[4]分别进行了盾构隧道双层衬砌的整环试验和多环轴向模型试验；张厚美等[5-7]通过模型试验和数值模拟方法，提出了接头抗弯刚度的理论评价方法和双层衬砌接头的相互作用模型，建立了圆形装配式一次衬砌的计算模型和装配整体式双层衬砌的受力计算模型，根据双层衬砌结合面处理方式提出层间压缩、剪压、局部抗弯3种双层衬砌相互作用模型；姚超凡等[8]在3种双层衬砌分析模型基础上，提出一种改进的梁-弹簧-层间压杆弹簧组合模型；晏启祥等[9]对比分析了层间梁、层间弹簧、层间压杆等多种双层衬砌数值计算模型，认为层间通过压杆弹簧组合连接计算更为合理；何川等[10]以狮子洋隧道为背景，采用模型试验和数值模拟相结合的手段，基于纵向等效刚度模型对软硬交界地层单、双层衬砌隧道纵向开展受力及变形研究；于清洋[11]通过开展模型试验对盾构隧道双层衬砌荷载分配状态进行研究，结果表明，在双层衬砌同步施作情况下，外荷载较小时管片与二衬受荷量值接近，外荷载较大时管片承担大部分荷载，二衬受力相对较小；王士民等[12]采用接触摩擦单元模拟双层衬砌结合面，建立复合式及叠合式双层衬砌三维实体非连续接触模型，并与模型试验比对，验证了数值模型的合理性；阳军生等[13]基于对双层衬砌取水盾构隧道现场测试数据，提出了一种适用于软土地层，能较为准确确定盾构隧道设计荷载的计算方法。

但针对盾构隧道二次衬砌施作时机的相关研究鲜有报道，国内外关于二次衬砌施作时机的研究集中于矿山法隧道，相关文献认为[14-17]矿山法隧道二衬合理施作时机应考虑以下两方面因素：一方面充分发挥围岩的自承能力，另一方面允许围岩产生一定变形，减少对支护结构的作用力，即矿山法隧道二衬合理施作时机要同时兼顾控制变形与荷载分担要求。由于盾构隧道所处地层特性、衬砌结构体系、施工过程等与矿山法隧道存在显著差异，因此，盾构隧道二次衬砌施作时机不宜直接借鉴矿山法隧道的相关结论。

鉴于此，依托国内首条全线敷设二次衬砌的大断面水下盾构隧道武汉地铁8号线越江盾构隧道工程，基于所提出的双层衬砌盾构隧道三维壳-弹簧力学分析模型[18]，设定不同的水、土荷载变化规律和二衬施作时间，根据实际工程施工顺序进行计算分析，探究变荷载条件下双层衬砌结构力学特性演变规律。

1 研究背景

1.1 工程概况

武汉地铁8号线越江隧道工程位于武汉长江二桥上游，为黄浦路站与徐家棚站区间隧道，全长约3 186 m，隧道上方江面宽约1 500 m。

衬砌采用5个标准块+2个邻接块+1个封顶块的分块形式。隧道下部设置口字形预制箱涵，箱涵以上设置0.3 m厚钢筋混凝土二衬，混凝土强度等级为C40，配筋均采用HRB400钢筋，环向钢筋φ22 mm，纵向钢筋φ12 mm，布置间隔均为200 mm。隧道横断面形式如图1所示。管片参数见表1。

选取里程DK11+454处断面作为研究对象，此断面为隧道江中最大埋深、最高水头断面。图2为研究断面地质剖面，上覆土厚19.47 m，拱顶距江水表面36.23 m，隧道下穿地层主要为粉细砂、圆砾土、强风化砾岩、弱胶结砾岩的复合地层。地层基本参数见表2。

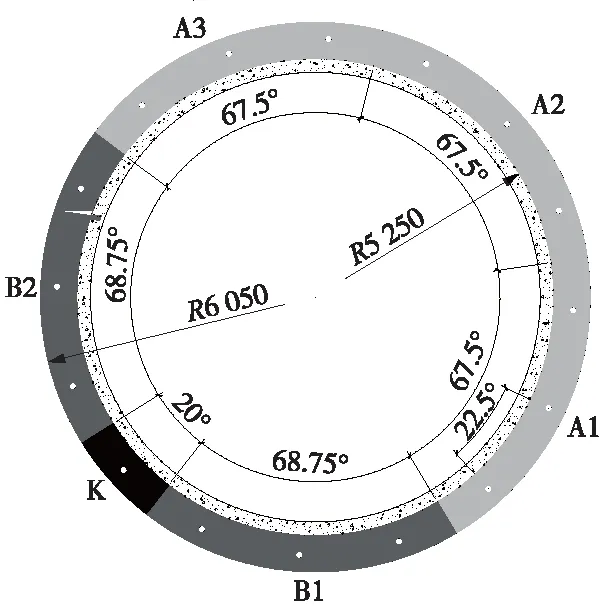
图1 隧道横断面(单位：mm)

表1 管片参数

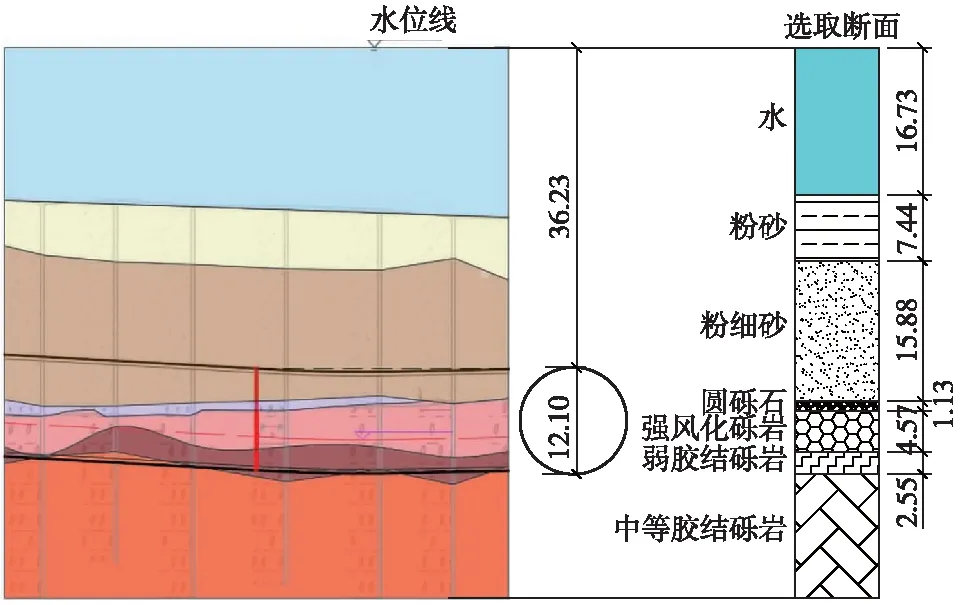
图2 里程DK11+454断面地质剖面(单位：m)

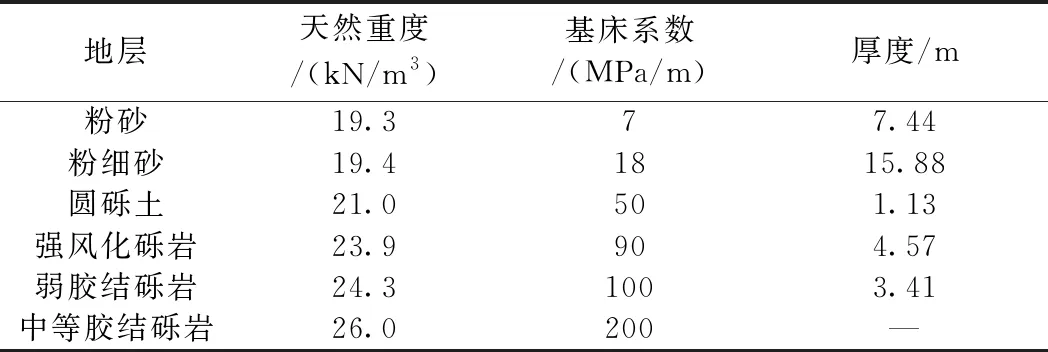
表2 地层基本参数

1.2 水土荷载变化规律

在河床淤积、冲刷及水位涨落等因素影响下，水下隧道的上覆水土荷载一直处于变化之中。以所选取计算断面为例，隧道上覆土以粉砂、粉细砂透水地层为主，厚度约19 m，管片拼装完成时江水表面距隧道拱顶约36 m。根据工程勘察报告、长江水位监测、武汉长江隧道河床监测等资料，计算断面处河床冲淤及水位变化关系如图3所示。

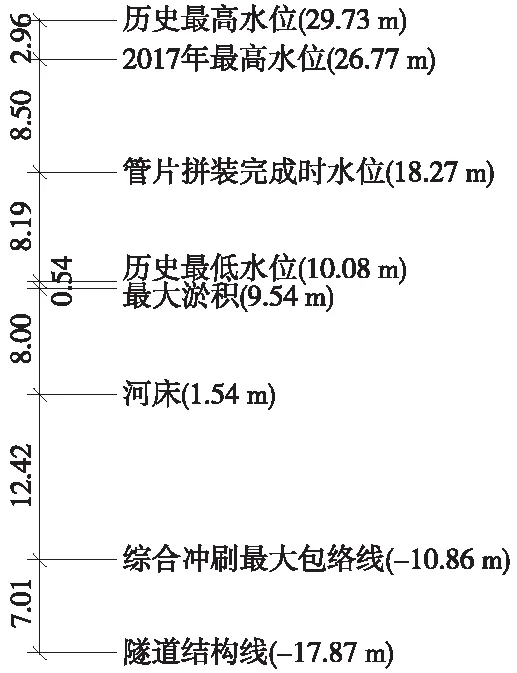
注：括号内数值为吴淞高程。图3 计算断面水位及冲淤变化示意(单位：m)

由图3可以看出，河床最大淤积厚度约8 m，最大冲刷深度约12 m，水位最大涨幅约10 m，水位最大降幅约8 m。对于水下盾构隧道双层衬砌结构而言，管片与二次衬砌形成联合承载体系，两者共同承担外部荷载变化量，故在上述外荷载变化条件下，双层衬砌结构管片及二衬结构受力状态与二次衬砌施作时机密切相关。

2 计算模型

2.1 参数取值

采用大型通用有限元软件ANSYS进行建模计算。由于盾构隧道管片具备一定厚度，且宽厚比一般小于5，宜采用厚壳单元进行模拟[13]，计算采用四节点塑性大应变单元shell43模拟管片及二衬，管片及二次衬砌的计算参数取值如表2所示。基于梁-弹簧计算模型方法，使用combin7三维销钉铰链单元模拟管片的环、纵向接头[19]，参考既有研究及工程参考实例，考虑盾构隧道尺寸、管片厚度及螺栓强度，确定数值计算所用抗弯刚度[20-21]。结合面的径向压杆和剪切弹簧分别采用Link10和combin14进行模拟，参照串联弹簧刚度法确定数值计算所用的结合面压缩、剪切刚度。管片接头及结合面计算参数取值分别如表3、表4所示。

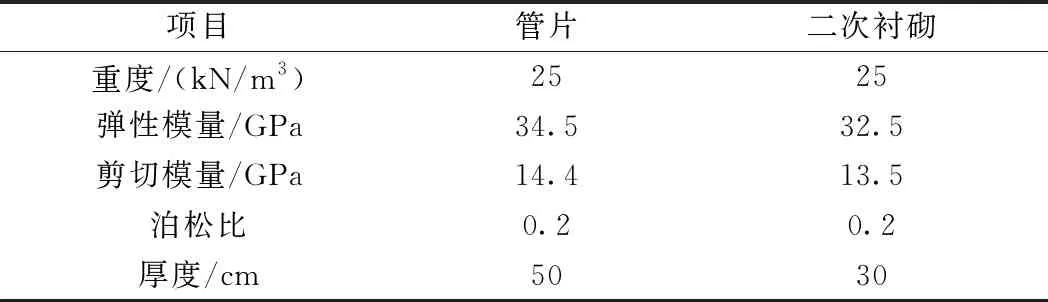
表3 管片及二次衬砌参数

表4 管片接头及结合面参数

对边界进行必要的约束：地层弹簧自由端约束全部方向自由度，管片、二衬拱顶及拱底约束水平及竖向位移，两端约束轴向位移，以符合平面应变基本假设。同时，在目标环前后建立半环长度的双层衬砌结构，以消除边界效应的影响。所建立模型如图4所示。

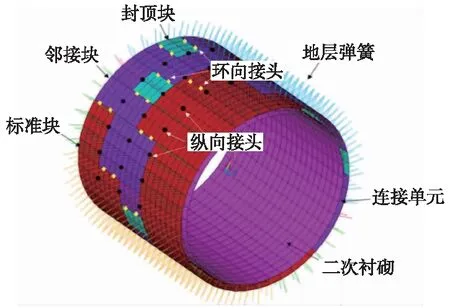
图4 数值计算模型

2.2 计算工况

基于计算断面处的外荷载变化规律，假定外荷载变化过程为：从原有荷载开始逐步增大至最终状态，最终状态为原有荷载+河床淤积10 m+水位上涨10 m。受施工工序因素影响，二次衬砌施作落后于管片较长时间，因此，二衬施作完成后的短时间内，外荷载100%由管片承担，二衬不发挥承载作用[22]。然而，由于荷载处于长期变化过程中，管片与二衬的承载比例也将因此发生变化。

具体计算工况如表5所示，通过设置不同的二衬施作时间，相应地改变二衬与管片之间的外荷载承载比例，比较不同工况下结构内力，分析其安全性。

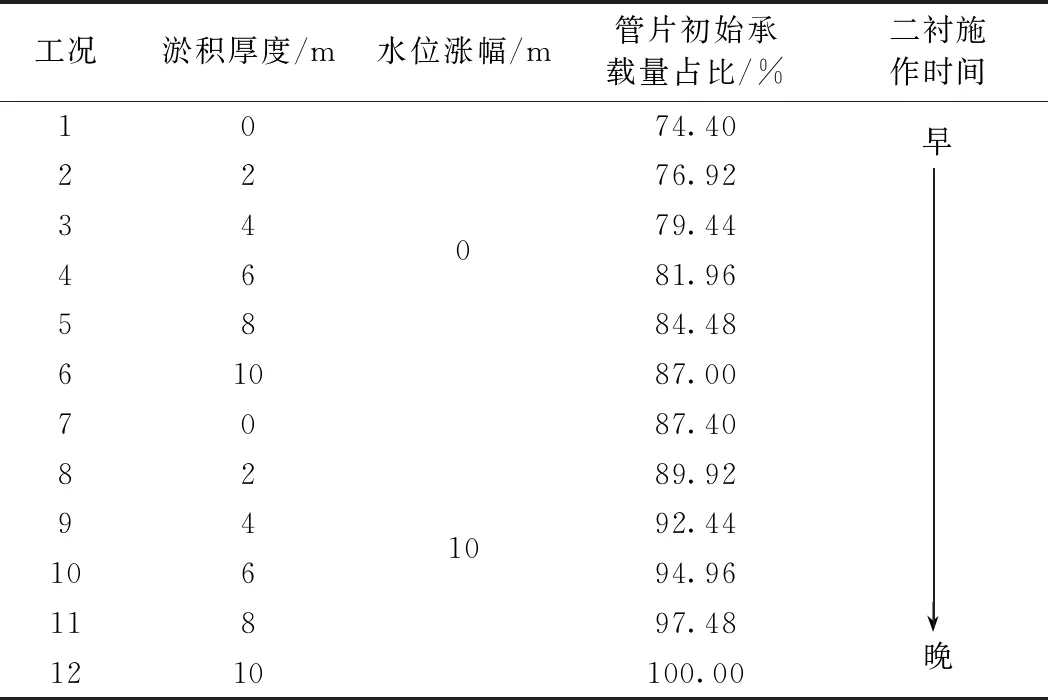
表5 计算工况

表5中的“淤积厚度”和“水位涨幅”代表二衬施作完成后，外荷载变化量的大小，“管片初始承载占比”表示在二衬施作时，管片(初支)承载的荷载对于最终荷载状态的荷载占比，与“淤积厚度”“水位涨幅”一一对应。例如：工况1模拟在原荷载下完成二衬施作，随后河床淤积10 m、水位上涨10 m，达到最终荷载状态；工况10模拟在河床淤积6 m、水位上涨10 m后完成二衬施作，随后河床淤积4 m达到最终荷载状态；工况12模拟在河床淤积10 m、水位上涨10 m后完成二衬施作，随后外荷载不再发生变化。

结合工程施工流程，计算分3个时间步进行：第一步(time1)，“杀死”二衬及层间连接单元，施加全部管片节点力，求解；第二步(time2)，基于第一步求解结果，“激活”二衬及层间连接单元，考虑二衬自重影响，再次求解；第三步(time3)，基于第二步求解结果，继续施加外荷载至最终状态。

3 结构内力计算结果分析

3.1 不同施作时机条件下管片衬砌结构受力特性

以工况1、工况12为例，管片衬砌轴力计算云图如图5所示。

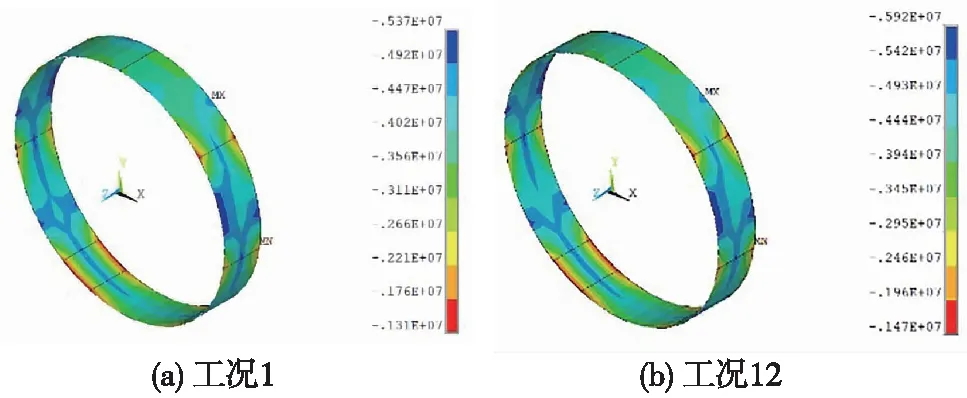
图5 管片轴力计算云图(单位：N)

由图5可知，不同二衬施作时机下，管片轴力分布规律相似但量值差异明显。受管片接缝影响，轴力的分布呈现出明显不连续性，在结构刚度较低的环、纵缝交接处，管片轴力明显降低，轴力峰值出现在幅宽中部位置。在河床淤积及水位上涨时，二衬施作较早(工况1)时的管片轴力小于二衬施作较晚(工况12)时的管片轴力。

管片衬砌最大轴力变化曲线如图6所示。

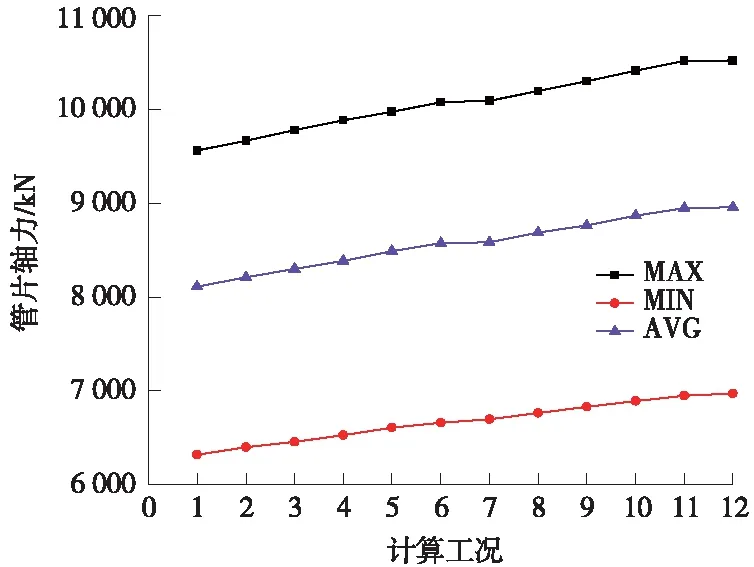
图6 管片衬砌轴力变化曲线

由图6可知，管片轴力随二衬施作滞后程度近似呈线性增长，即二衬施作越早管片轴力越小，二衬施作越晚管片轴力越大。当管片承担74.40%外荷载即施作二衬时，管片平均轴力量值较低，为8 111.91 kN；当管片承担87.00%外荷载后再施作二衬时，管片平均轴力为8 572.61 kN，提高了近5.7%；当管片承担全部100%荷载后再施作二衬，管片平均轴力量值最大，为8 959.52 kN，增大10.5%。

以工况1、工况12为例，管片衬砌弯矩计算云图如图7所示。

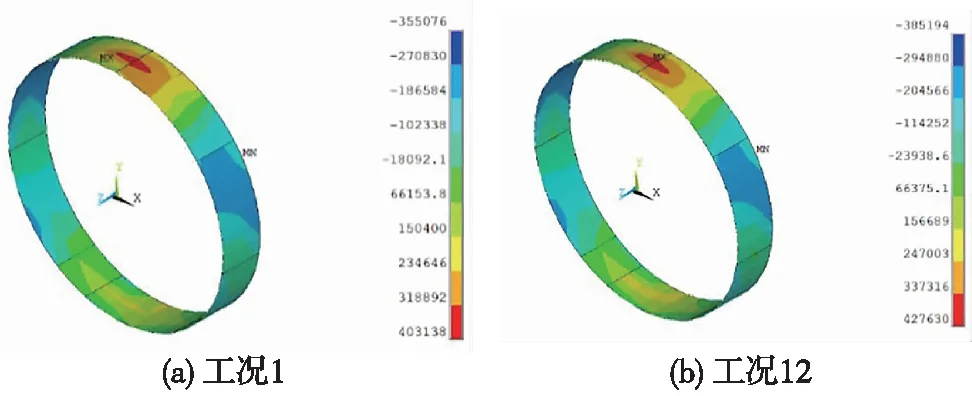
图7 管片弯矩计算云图(单位：N·m)

由图7可知，不同二衬施作时间下，管片弯矩分布规律相似，且量值差异较小。管片弯矩分布呈“上大下小”规律，且受接缝影响，其分布仍呈现出明显不连续性。最大正弯矩分布区域明显，出现在拱顶的纵向接缝处；最大负弯矩则出现在上拱腰部位，分布区域较小，与纵向接缝仍有一定距离。在河床淤积及水位上涨时，二衬施作较早(工况1)的管片弯矩小于二衬施作较晚(工况12)的管片弯矩。

管片衬砌弯矩变化曲线如图8所示。

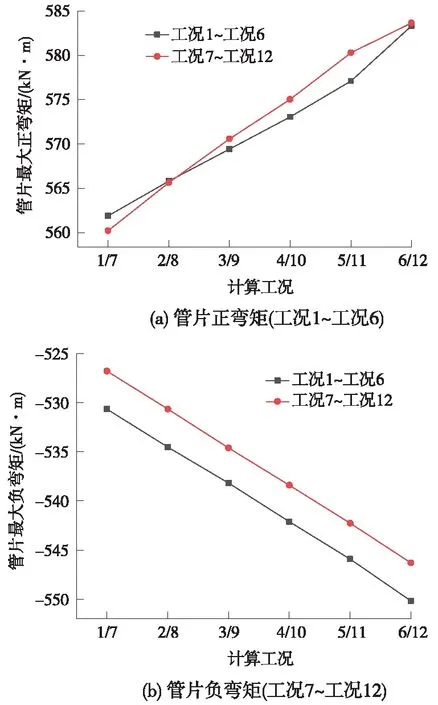
图8 管片衬砌弯矩变化曲线

由图8可知，对于工况1～工况6或工况7～工况12而言，管片弯矩随二衬施作滞后程度近似呈线性增长，二衬施作越早管片弯矩量值越小，二衬施作越晚管片弯矩量值越大。当管片承担74.40%外荷载时施作二衬(工况1)，管片最大正弯矩量值较低，为561.89 kN·m；当管片承担87.00%外荷载后再施作二衬(工况6)，管片最大正弯矩为583.33 kN·m，提高了3.8%。由管片弯矩变化量可知，二衬施作时机早晚对管片弯矩改变幅度较小。

对比工况1～工况6与工况7～工况12管片弯矩可知，低水位条件下施作二次衬砌(工况1～工况6)与高水位条件下施作二次衬砌(工况7～工况12)时，管片正负弯矩的量值差异较小。如在水位上涨10 m，河床淤积10 m时(工况12)施作二衬，管片最大正弯矩为583.66 kN·m，较工况6弯矩量值非常接近。因此，在不同水位施作二次衬砌，对管片的正弯矩影响几乎可以忽略。工况1～工况6与工况7～工况12管片负弯矩变化曲线接近平行，两者的差值波动较小，而对于正弯矩变化曲线而言，两曲线的差值波动较大。这是因为，最大正弯矩出现的位置在拱顶纵缝处，该位置结构刚度骤降，变形量较大，因此，其弯矩变化亦呈现出显著的非线性特点。

3.2 不同施作时机条件下二次衬砌结构受力特性

以工况1、工况12为例，二次衬砌轴力计算云图如图9所示。

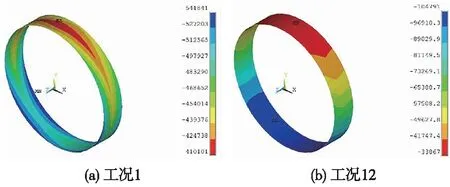
图9 二次衬砌轴力计算云图(单位：N)

由图9可知，受不均匀地层影响，二衬轴力在环向呈上小下大分布规律。此外，施作时机对二衬内力分布规律和量值大小有重要影响。当二衬施作较早(工况1)时，其承担的外荷载值较大，轴力量值较大，且轴力分布受环向接缝影响非常明显，在纵向上呈环缝处轴力大、幅宽中央处轴力小分布规律；当二衬施作较晚(工况12)时，其承担的外荷载值较小，轴力量值较小，在环向上呈上小下大规律分布，在纵向则均匀分布，此时，二衬轴力受管片接缝影响较小，主要受自重影响。

各工况下二次衬砌轴力变化曲线见图10。

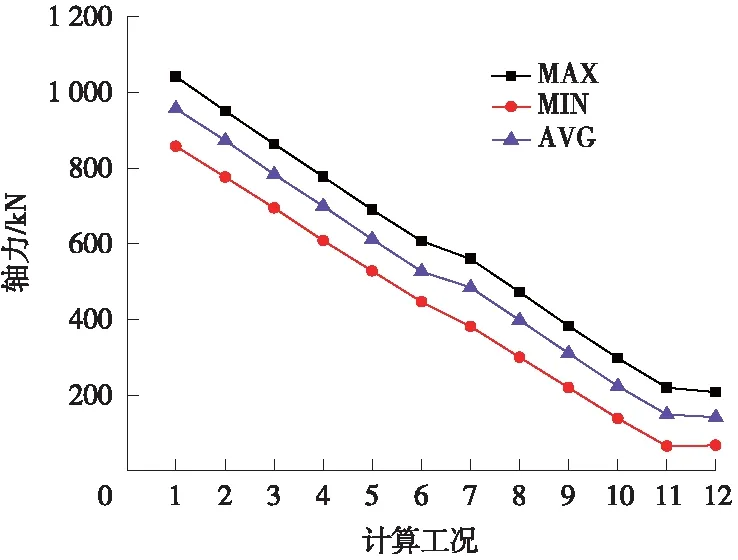
图10 二次衬砌轴力变化曲线

由图10可知，二衬轴力随结构施作滞后程度近似线性降低，即二衬越早施作其自身轴力越大，二衬越晚施作自身轴力越小。当管片承担74.40%外荷载即施作二衬时，二衬平均轴力量值最大，为956.49 kN；当管片承担100%外荷载后再施作二衬，二衬不承担外荷载，平均轴力量值最小，为141.41 kN，约为最大平均轴力的14.8%。由此可见，在河床淤积及水位上涨情况下，双层衬砌盾构隧道二衬施作得越早，二衬能够分担更多的荷载增量，承载功能发挥得越充分，可降低管片受力水平。

以工况1、工况12为例，二次衬砌弯矩计算云图如图11所示。

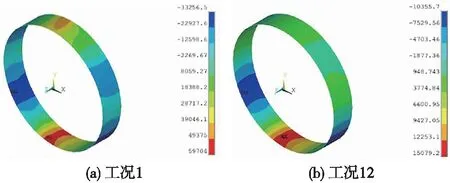
图11 衬砌弯矩计算云图(单位：N·m)

由图11可知，施作时间对二衬内力分布规律和量值大小有重要影响。当二衬施作较晚时(工况12)，由于管片承担100%外荷载作用，二衬仅承受自重，拱脚处负弯矩值最大，拱底正弯矩值最大，拱顶正弯矩较小且分布较为均匀；当二衬施作较早时(工况1)，由于管片仅承担74.4%外荷载作用，其余25.6%外荷载由双层衬砌结构共同承载，此时二衬不仅承担自重，在外荷载作用下其弯矩量值显著增大，且弯矩分布规律亦发生明显变化，表现为拱顶及拱底内侧受拉，拱底正弯矩最大，拱顶正弯矩值显著增大，两侧外侧受拉，拱脚负弯矩最大。

各工况下二次衬砌弯矩变化曲线见图12。

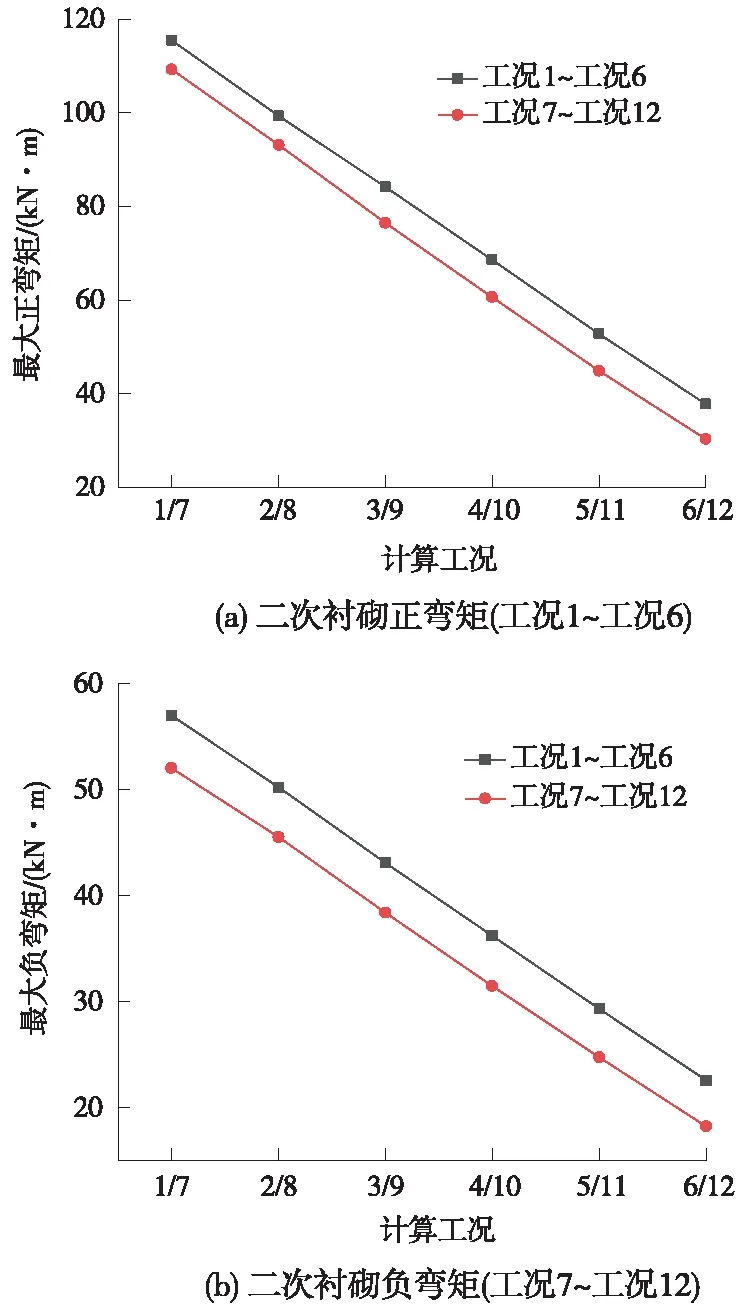
图12 衬砌弯矩变化曲线

由图12可知，在河床淤积及水位上涨情况下，二衬弯矩随二衬施作滞后程度近似呈线性降低，施作越晚弯矩越小，施作越早弯矩越大。当管片承担74.40%外荷载即施作二衬时(工况1)，二衬最大正弯矩量值最高，为115.46 kN·m；当管片承担87.00%外荷载后再施作二衬时(工况6)，二衬最大正弯矩为37.78 kN·m，降幅约为67.3%。由二衬弯矩变化量可知，二衬施作时机早晚对其弯矩影响较大。

对比工况1～工况6与工况7～工况12二衬弯矩可知，低水位条件下施作二次衬砌(工况1～工况6)与高水位条件下施作二次衬砌(工况7～工况12)时，二衬弯矩量值有明显的差异。在水位上涨10 m、河床淤积10 m时施作二次衬砌(工况12)，二衬最大正弯矩量值最小，为30.29 kN·m，与工况6相比降低了20.6%，而与工况7相比降低了243%。这说明河床淤积对二衬弯矩的影响远大于水位涨幅的影响。工况1～工况6与工况7～工况12弯矩变化曲线接近平行，可知两者的差异主要受二衬施作时水位影响，而与河床淤积无关。这说明水位涨幅与河床淤积对于二次衬砌弯矩影响是相互独立的。

3.3 小结

综合上述分析可知，在水位上涨和河床淤积影响下，随着二次衬砌施作时机的提前，二衬所承担的外荷载值越大，受管片接缝影响，管片、二次衬砌内力分布规律亦呈现出显著的不均匀性，管片轴力量值分布规律表现为接缝处较小，幅宽中部处较大，而二衬轴力量值分布规律表现为接缝部位较大，而幅宽中部处较小。

随着二衬施作时机的提前，管片承担的外荷载值减小，管片轴力、弯矩量值都有一定程度降低，可有效降低管片混凝土截面压应力，降低管片发生受压破坏的风险。但由于轴力降幅(最大10.5%)高于弯矩降幅(最大3.8%)，因此，管片混凝土截面拉应力有所增加，此时管片容易发生偏心受拉破坏。因此，在二衬施作时机较为提前的情况下，应对管片配筋进行适度加强。

随着二衬施作时机的提前，二衬承载的外荷载值较大，二衬轴力、弯矩量值有明显增大，显著提高了二衬混凝土截面压应力，此时二衬易发生受压破坏。但由于二衬轴力增幅(最大397.5%)远大于弯矩增幅(205.6%)，降低了二衬混凝土内拉应力，对防止二衬混凝土偏心受拉破坏有利。因此，在二衬施作时机较为提前的情况下，应考虑提高二衬混凝土强度等级。

对比淤积条件相同，水位涨幅条件不同工况(工况1～6与工况7～12)可知，在不同水位条件下施作二次衬砌对管片弯矩影响较小，而对二次衬砌弯矩有显著影响，在低水位条件下施作二衬，其弯矩量值的变化幅度相对较大(20.6%)，因此，水位涨幅对于二衬弯矩的影响显著高于管片弯矩的影响。对比水位涨幅条件相同，淤积条件不同的工况可知，在不同淤积条件下施作二次衬砌，管片弯矩量值有一定变化(幅度3.8%)，而二次衬砌的变化非常显著(幅度243%)，这说明在不同淤积条件下施作二次衬砌，二衬内力变化幅度显著高于管片。