基于改进Dijkstra算法的医院智慧停车路径规划研究
2022-07-12汪厚俊郑明飞
汪厚俊, 郑明飞
(1.南京卓欧信息技术有限公司, 江苏, 南京 210000; 2.南京市妇幼保健院, 江苏, 南京 210000)
0 引言
随着现代信息化的发展,物联网技术广泛应用于各大领域。但受行业限制,部分行业的物联网技术应用程度较低,尤其是在医院停车场智慧管理方面,物联网技术没有得到有效应用,导致用户无法全面获取停车场车位相关信息。此外,由于医院停车场内没有提供相应的车位推荐和行驶路径指引服务,无法使用户实现高效、快速停车。因此,基于物联网技术的停车场车位推荐和行驶路径指引对于医院智慧停车管理十分重要。目前,基于物联网技术的路径规划算法主要包括A*算法和蚁群算法算,如李世国等[1]、宋宇等[2]结合改进A*算法与无人机飞行特点,对无人机飞行路径进行规划,获得飞行时间少、路径长度短的无人机航路,缩短了传统路径规划方法的时间。但该算法容易陷入局部最优,且其启发函数难以确定,难以应用于实际医院停车管理路径规划中。马小铭等[3]、龚铭凡等[4]基于改进蚁群算法,通过引入各路径段与起始点和目标点连线的夹角信息,获得了一种具有高搜索效率和质量的路径规划方法。但该方法存在计算量大的问题,不适用于医院智慧停车的行驶路径和最优车位规划。近年来,随着Dijkstra算法在复杂图论中的应用,研究通过改进该算法得到一种容易实现且简单易懂路径规划方法,并将其用于与医院智慧停车管理最优车位的行驶路径规划,实现了医院智慧停车管理。
1 智慧停车路径规划问题描述
智慧停车服务的本质,就是在停车场内为驾驶员提供有效的路径规划。目前,为提高停车场的服务水平,部分停车场引入停车服务系统对高峰期的停车进行引导,以免造成停车场出现局部拥堵的情况。而对未引入停车服务的停车场,传统的方法是驾驶员采用目光瞭望的方法寻找车位。如驾驶员没找到合适的车位泊车,会继续搜索下一个空闲车位。这样的停车方式不仅耗费时间长,还会出现无用交通,增加停车场内高峰期的交通压力,也影响驾驶员的心情。具体搜寻流程如图1所示。
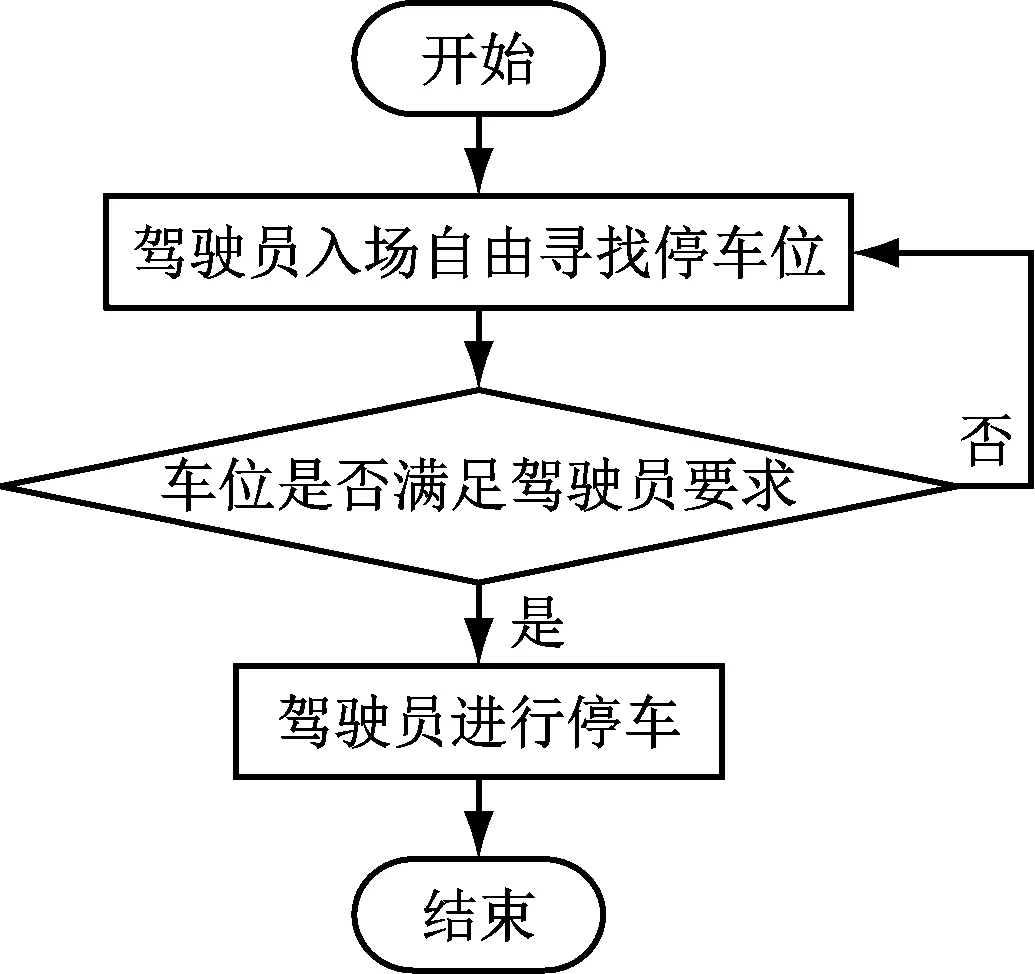
图1 传统目光瞭望搜索车位流程
为解决这种无效泊车问题,如当驾驶员进入停车场时就进行车辆停车路径规划,根据停车场中车位空闲数量,计算出一个路径最短的停车位,这样不仅可减少驾驶员的泊车时间,还可减少尾气排放。具体的智能引导流程如图2所示。
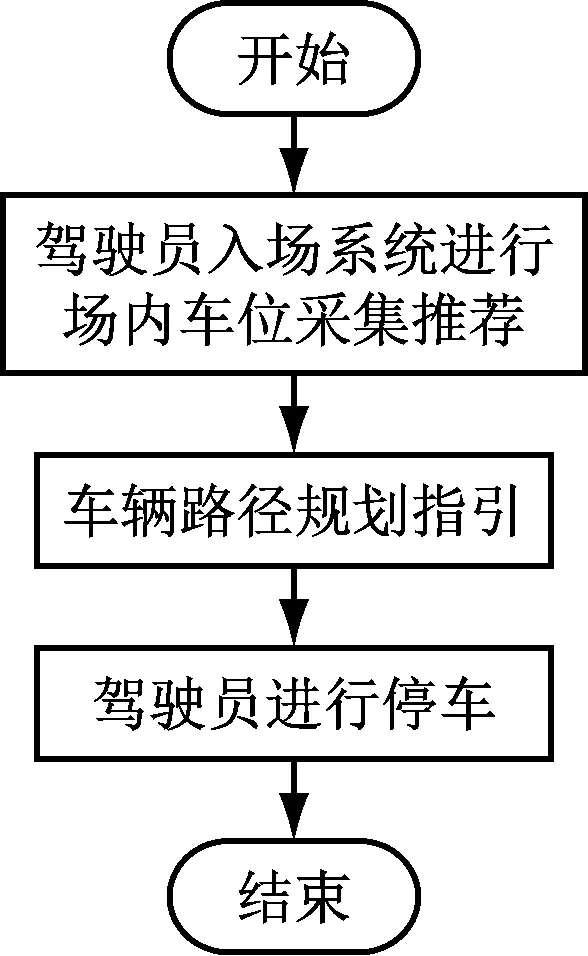
图2 智能停车服务流程
从图1、图2可以看出,对有车辆引导的停车场,驾驶员停车具有很强的目的性,即在场内有空余车位的情况下,找到最近的车位,避免无效的车位搜索。所以智能停车路径规划的本质,就是在空闲车位的情况下,给驾驶员找到一条最短的停车路径,让驾驶员在最短时间停车,避免造成高峰期的停车拥堵问题。
2 基于Dijkstra算法的停车路径规划
2.1 Dijkstra算法简介
Dijkstra算法是用于计算最短路径的经典算法,主要用于解决有权图中最短路径规划问题和网络内部路由问题,现常用于辅助解决较为复杂的图论问题[5]。Dijkstra算法包括永久标号和临时标号2种方式,通过贪心思想在全局范围内搜索最优解,其搜索过程如图1所示。首先,确定起始源节点为圆心,采用同心圆的方式向周围搜索,直至所有节点全部位于同心圆所在的搜索域内。Dijkstra算法搜索域即算法的搜索范围,如图3中最外层的实线圆包含的范围。

图3 Dijkstra算法搜索区域
2.2 传统Dijkstra算法在停车路径规划的描述
采用传统Dijkstra 算法规划停车场泊位路径规划时,其基本的思路为令路网模型中,源节点为y,目标节点为m,Si表示y到m的最短路径权值,Vi表示y到m前一个节点,(Si,Vi)表示路网模型中的节点,则Dijkstra算法具体搜索步骤如下:
① 设置最短路径源节点Sd为0,Vd=Ø,标记k=y。假设其余节点未标记,则Si=∞,Vj未知;
③ 当路网模型中所有节点全部标记,结束算法。
2.3 Dijkstra算法改进
标准Dijkstra算法通过依次递增的方法实现了所有节点的搜素,但由于其搜索方向不确定且搜索范围在搜索过程中不断扩大,降低了搜索效率。因此,为实现医院智慧停车管理车辆最短路径规划,研究对Dijkstra算法进行了搜索范围和搜索方向2个的优化[6]。
2.3.1 搜索范围优化
通过上述对Dijkstra算法的分析可知,该算法在整个搜索过程中没有考虑起始节点和目标节点的位置,故其搜索的范围较大,增加了算法的计算难度。因此,为避免因搜索范围过大带来计算问题,研究在Dijkstra算法中加入位置关系,采用双向搜索方法缩小其搜索范围。但由于双向搜索在路网模型中,其搜索目标节点和其他节点的成功率相同,因此为进一步缩小搜索范围,研究提出扇形优化的方法,如图4所示,其近似表示为以源节点为圆心的层层圆弧,通过减少搜索过程中的无用节点,实现缩小搜索范围。
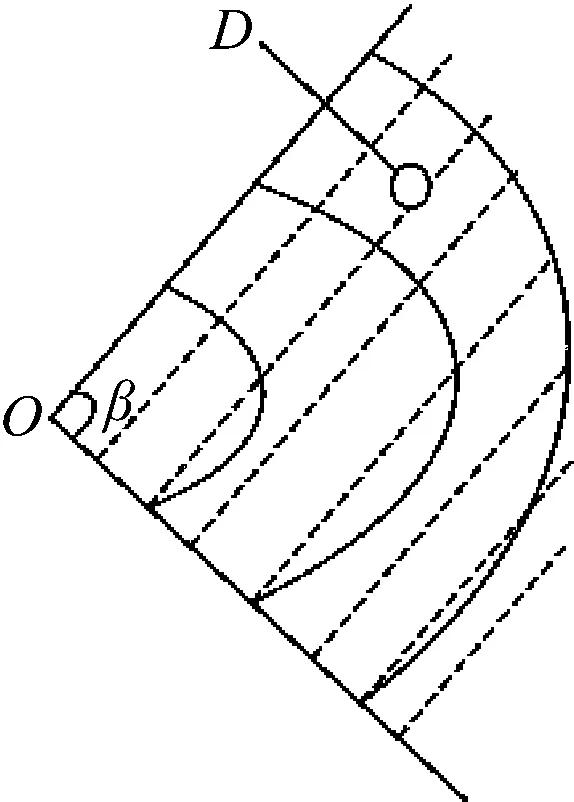
图4 改进Dijkstra算法搜索区域
2.3.2 搜索方向优化
研究通过引入约束函数,采用源节点和目标节点正反2个方向交替进行搜索的方式对Dijkstra算法搜索方向的优化。通过采用约束函数,可快速适应实时信息变化引起的权值变化,减少无效节点的搜索,进而提高车辆路径引导服务的搜索速率。约束函数表达式如式(1)。
Q(n)min=q(n)+a(n)
(1)
式中,q(n)表示起始或目标节点到搜索终止区域节点的最优路径权值,a(n)表示搜索区域内的节点数目。
2.4 基于改进Dijkstra的停车路径规划模型构建
根据区域划分方法的划分标准,定义道路交叉点和车位节点为iD ,采用改进Dijkstra算法引导医院停车场内车辆寻找最优车位的路径基本思路是:当车辆进入医院停车场时,车辆引导服务首先在起始入口根据采集到的车辆信息判断该车辆是否有预约车位,然后根据车辆信息、车位信息和场内道路信息,采用改进Dijkstra算法确认最优车位,最后实现停车智慧管理[7-8]。具体步骤如下。
① 确定路网汇总源节点y与目标节点m,设置源节点坐标为yi=(yXi,yYi),目标区域节点坐标为mi=(mXi,mYi),车位道路节点坐标为di=(dXi,dYi)。由欧式距离公式(2)可计算出目标区域车位的道路节点与源节点距离[9]。
(2)
筛选出目标区域车位道路节点与源节点距离的最大值ndistmax,则改进Dijkstra算法扇形优化的轴线即为ndistmax构成的直线。
ndistmax=max{|yi,mi|}
(3)
为确定扇形搜索角度,研究建立如图5所示的数学模型。
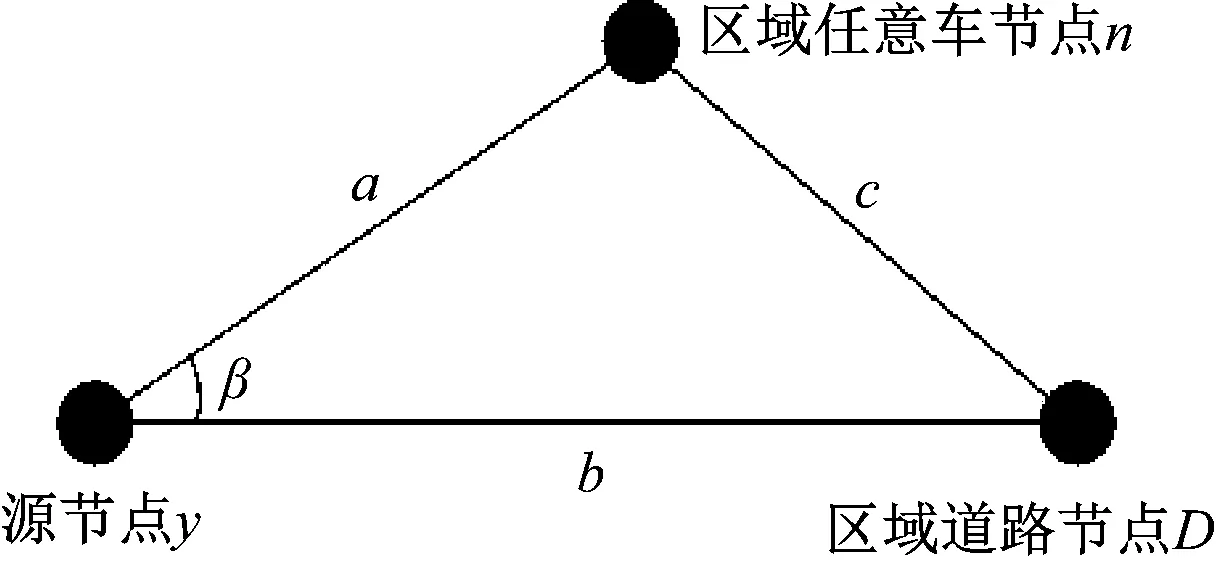
图5 扇形搜索求解数学模型
② 初始化正向和反向搜索节点集合E1和E2以及终止区域节点集合L。
③ 根据三角公式确定扇形搜索角度a。
④ 分别从起始节点和目标节点2个方向进行搜索,当E1、E2集合满足L=E1∩E2≠Ø时,停止搜索。
⑤ 在集合中查找t,通过计算获取最小ym=yt+tm值。最后根据E1、E2集合确定源节点和目标节点的最优路径。
3 仿真实验
3.1 参数设置

(3)
(4)
3.2 算法性能比较
根据式(3)、式(4)可计算得到标准Dijkstra算法和改进Dijkstra算法的起始节点与终止节点的欧式距离关系以及有效搜索区域,如图6所示。由图6可知,随起始点与目标节点距离增大,改进Dijkstra算法的搜索有效范围明显优于标准Dijkstra算法的搜索有效范围,其遍布的无用区域相比标准Dijkstra算法大幅度减少,说明改进Dijkstra算法可有效缩小搜索范围。

图6 不同算法搜索范围比较
在搜索时间仿真实验中,研究在同样的仿真条件下,采用两种算法计算其搜索时间,并绘制其欧式距离与运行时间的对比图,如图7所示。由图可知,改进Dijkstra算法平均运行时间明显低于标准Dijkstra算法,且随起始节点到目标节点距离增加,其优势更加明显,说明改进Dijkstra算法可有效缩短路径规划搜索时间。

图7 不同算法平均运行时间对比
3.3 实例验证
为验证本研究提出的Dijkstra算法性能,研究现场采集某市医院停车场某一区域进行了车辆和车位信息采集,如图8所示。图中包括车位状态信息、道路车辆信息等。

图8 某时刻医院停车场车位分布图
(1) 决策属性确定
医院智慧停车管理系统分配驾驶员车位主要由行车时间、停车难度、步行距离3个因素决定,因此,本研究选取上述3个因素为最有车位推导的决策属性。
(2) 获取停车场内车辆及车位信息
利用改进Dijkstra算法获取实时医院停车场内车辆与车位信息,确定停车场内有效车位为a1、b2、c3、e4、e5、g6、h7、h8、h9、k10、k11、k12;移动车辆分布在d1-d2、d3-d4、d5-d6、d7-d8、d4-d9、d10-d11、d8-d13、d13-d14段。
(3) 计算道路与车位决策属性值
根据道路边权构造方法[10],计算医院停车场内路段道路属性,结果如表1所示。

表1 医院停车场道路属性信息
根据以上权值信息,通过邻接矩阵公式,建立式(5)的医院停车场邻接矩阵dij。
(5)
根据停车场内车辆实时位置信息及车位难度赋值,可计算得到有效车位的属性信息,如表2所示。

表2 有效车位属性表
根据有效车位有效属性,采用改进Dijkstra算法在MATLAB软件中进行仿真,即可得到车位属性中的行驶路径。如k10车位,其行驶路径如图9所示。由图可知,k10车位的行驶路径为d1-d5-d10-d11-d12。当车辆到达k10车位后,车位指示灯显示开放。

图9 k10车位行驶路径示例
(4) 最优车位路径有效性分析
为验证提出的改进Dijkstra算法推导出最优车位行驶路径的有效性,研究对比传统最短路径算法,选取同一时刻医院停车场内车辆和车位信息,并使用MATLAB计算得到不同算法最佳车位与最优路径,如图10所示。由图10可知,改进Dijkstra算法求解的车位为h7,车位到入口距离为40 m,行驶路线为s-d1-d5-d10-h7,用时19 s;传统最短路径算法求解的车位为b2,车位到入口距离为36 m,行驶路线为s-d1-d2-b2,用时61 s。由此可得,本研究提出的改进Dijkstra算法虽行驶距离略高于传统最短路径算法行驶距离,但大幅度降低了行驶时间,有效避免了因行驶时间过长造成的医院停车场内拥堵情况,说明改进Dijkstra算法推导的最优车位有效规避了停车场内流量大的问题,同时可满足驾驶员快速完成停车,进而有利于停车场管理人员对场内车位及车辆的管理,实现医院智慧停车管理。

(a) 改进前
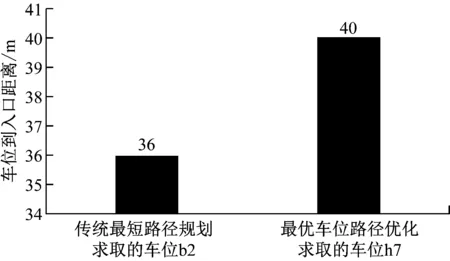
(b) 改进后图10 改进Dijkstra算法前后的最优路径
4 总结
综上所述,本研究提出改进Dijkstra算法预先推导得到医院停车场内最优车位及行驶路线,实现用户高效、快速的场内停车,且相较于传统最短路径算法计算的最短路径,该方案有效规避了因停车场内各区域流量不同造成的拥堵问题,更能满足用户实际需求及医院智慧停车的管理。
