基于CNN卷积神经网络的电力通信网故障诊断

邵淦, 吴昊， 姚朔晔

(国网宁波供电公司， 宁波 315000)

0 引言

电力通信作为保障电力运行的重要枢纽，是电力建设和保障的重点。伴随着电力通信规模的扩大，通信设备不断增加，从而使得驾驭电力通信网的难度也逐步增加。因此，如何保障电力通信网的通信以及如何及时对通信网出现的故障进行诊断与定位，是当前电力智能化建设和思考的重点。传统的电力通信网故障诊断通过建立规则库的方式判断，但这种规则库主要依赖于人工经验。而随着人工智能的兴起，深度学习算法在处理非线性问题方面的优势开始逐步体现。如唐斯等[1]提出基于深度学习算法，利用注意力与多尺度卷积神经网络对电机轴承故障诊断，实现了电机轴承故障的快速诊断。石赫等[2]基于深度学习，对非线性电网故障进行了准确定位。基于此，本研究提出一种基于CNN卷积神经网络的电力通信网故障诊断模型，以实现对电力通信网的故障诊断。

1 基本方法及原理

1.1 CNN神经网络

CNN神经网络由卷积层、池化层、全连接层三层结构组成[3]。其中，卷积层是整个网络的核心层，主要负责提取图像特征，其数学描述如式(1)：

y=f(∑wijx+b)

(1)

式中，x、y分别表示该网络层的输入和输出图像特征,wij表示二维卷积核,b表示偏置项,f(·)表示激活函数，通常为tanh函数、sigmoid函数、ReLU函数，但由于前2种函数收敛速度缓慢，且容易梯度消失，因此本研究中采用ReLU函数，具体表达式为

f(x)=max(0,x)

(2)

池化层分为平均池化和最大池化2个大类[4]，主要负责强化卷积层提取的图像特征，以提高模型的泛化能力。在本研究中，采用最大池化采样，数学表达式为

y=f(βdown(x)+b)

(3)

式中，x、y分别表示池化输入特征和卷积层输出特征,β、b分别表示乘性和加性偏置项,down(·)表示池化函数。

全连接层的作用是通过连接的神经元组合图像局部特征，实现分类并输出分类结果。其数学描述如式(4)。

y=f(wx+b)

(4)

式中，y表示全连接输出,f(·)表示激活函数,x表示全连接层输入,w表示权值,b表示偏置项。本文的全连接层采用softmax函数[5]。

CNN网络训练的具体流程如下：

(1) 设置网络初始参数，并输入网络；

(2) 计算模型输出值与目标输出值的误差；

(3) 当误差小于期望值时，结束训练，并输出固定权值和阈值；反之，则反向传播误差，并更新权值，重复步骤(2)和步骤(3)，直至误差小于期望值，结束训练。

2 基于CNN通信故障诊断模型构建

2.1 构建思路

基于CNN通信的故障诊断模型构建方法，首先利用故障状态矩阵对整个网络故障状态进行表征，并添加根源故障标签[6]。其次，利用CNN网络提取故障特征。然后，计算输出结果与真实标签向量的误差。最后，利用softmax分类器输出诊断结果。

2.2 告警数据处理与编码

考虑到原始告警信息数据中存在大量噪声等干扰信息会对模型训练造成影响，研究对这些数据进行选取与标准化、时间同步、加权编码的处理，具体处理方式如图1所示。

(1) 告警数据选取与标准化

结合当期获取的电力通信网告警信息特征，本研究对告警数据处理与标准化处理具体实现方法如下。首先，将采集到的原始告警信息输入数据库，选取与故障诊断相关的数据；然后，根据本研究定义属性值和字段名对所有选取的数据进行标准化处理，即实现了对原始告警数据的初步处理。在告警数据标准化阶段，研究根据字段值对最终诊断结果的影响程度，选取了5个对诊断结果影响较大的字段作为每一条告警信息的标识[7-8]。告警数据标准化选取的告警字段及其对应属性值如表1所示。

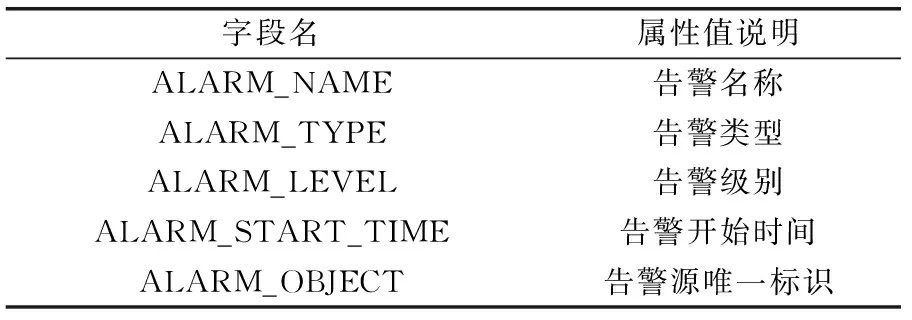
表1 标准告警字段及属性值

(2) 时间同步

(3) 告警数据编码

告警数据编码主要是表明每种告警对故障诊断的重要性。研究根据告警信息不同级别和类型对告警信息进行加权，以表征故障重要程度。但实际故障诊断中，由于存在如设备板卡脱位时根因告警等次要告警，而这类告警对故障诊断十分重要，因此本研究利用历史数据，设定每种告警对故障诊断的重要性，并通过式(5)对所有故障诊断影响权值进行计算。

(5)

式中，wA表示告警A对故障诊断影响权值,k表示故障种类,wi表示告警A对第i中故障的权值,nA表示wi不等于0的个数。

考虑到编码规模，研究仅选取了其中8种权值较大的告警类型进行编码，并根据告警权值大小进行优先级排序和二值化编码，得到如表2所示的编码结果。

表2 告警编码

采用图论邻接矩阵表征站点拓扑连接关系。设一个有n个站点的图为G，其顶点集、邻接矩阵、边集分别为V(G)={v1,v2,…,vn}、A(G)=(aij)n×n、E(G)。

其中：

(6)

编码故障时刻每个站点的告警事务为T(G)=diag{t11,t22,…,tnn}，tii表示站点vi的告警事务编码。定义故障状态矩阵为F(G)，可通过式(7)计算。

V(G)={S1,S2,S3,S4,S5}

(7)

假设站点集V(G)={S1,S2,S3,S4,S5}中S1丢失接收测光信号，则该时刻各站点对应的告警事务编码如表3所示。

表3 各站点告警事务编码

由式(6)可知邻接矩阵为

(8)

根据故障时刻告警实物编码可知：

(9)

由式(7)可知故障状态矩阵为

(10)

完成告警数据编码后，添加其对应的根源故障标签即可实现关联根源故障与告警。将所有故障时刻告警事务进行编码，即可得到CNN网络训练样本集。故障类型标签编码如表4所示。

表4 故障类型标签编码

2.3 基于CNN网络的特征提取

基于CNN网络主要通过卷积操作实现特征提取输入网络的故障状态矩阵不同类别的故障特征图[8]。当卷积核越多时，提取到不同层面的特征就越多，就越容易挖掘出故障和告警的特征关联，故本研究采用多核进行卷积操作。多核卷积操作如图2所示。

图2 告警数据处理流程图

最大池化层主要功能是减少图的特征维度，保留图的重要特征[9]。其具体池化操作如图3所示。

图3 故障特征最大池化

通过最大池化操作，整个卷积神经网络已经提取到n1，n2，…,nk等k个不同故障类别的特征图。但由于这k个特征图仅由故障状态矩阵中局部像素获得，只能反映故障类别的局部特征，而故障特征的完全类别特征并没有表示出来，因此需要通过全连接层加权处理组合这些局部故障类别特征，并利用softmax分类器进行分类，得到每个故障更全面的特征。根据故障类别(6类)，本研究建立的softmax分类器包含6个神经元，分别对应T1、T2、T3、T4、T5、T6不同故障类别标签，如图4所示。

图4 全连接加分类器

对于故障站点标签，本研究中除softmax层输出维度的网络结构参数不同外，含1×6的故障类型标签向量，其余参数均与故障站点标签分类的训练网络一致。

2.4 CNN的电力通信网诊断构建

2.4.1 诊断模型

考虑到本研究的故障样本数据量有限，且故障状态矩阵为11×11，较为简单，故本研究设计基于CNN的电力通信网故障诊断模型结构较为简单，如图5所示，具体每一层的网络参数如表5所示。表中，C1、C2表示卷积层；P1、P2层表示池化层；FC表示全连接层。

图5 基于CNN的电力通信网故障诊断模型

表5 基于CNN的电力通信网故障诊断模型参数

输入层输入图像输出的是维度为1×1×11单通道灰度图片。C1的卷积核在卷积前补充一圈0给输入的图片四周，以避免图像边缘的像素过多参与卷积导致的边缘信息大幅丢失，确保输出特征图保持原始图片的大小，长和宽均为(11+2-3)/1+1=11。由于C1层的卷积核为32个，因此其通道数为32个。C2层的输出特征图长宽均为(5+2-3)/1+1=5。P1层的输出特征图长宽均为(11-2)/2+1=5，由于其输入为C1层输出，因此其通道同样为32个。P2层的输出特征图长宽为(10-2)/2+1=5。FC含1 024个神经元，故其输出为 1×1 024。softmax分类层输出维度为1×6。

2.4.2 诊断模型实现

采用上述方法搭建基于CNN的电力通信网故障模型，并利用采集的告警数据对其训练和测试。模型训练和测试具体流程如图6所示，主要分为以下步骤。

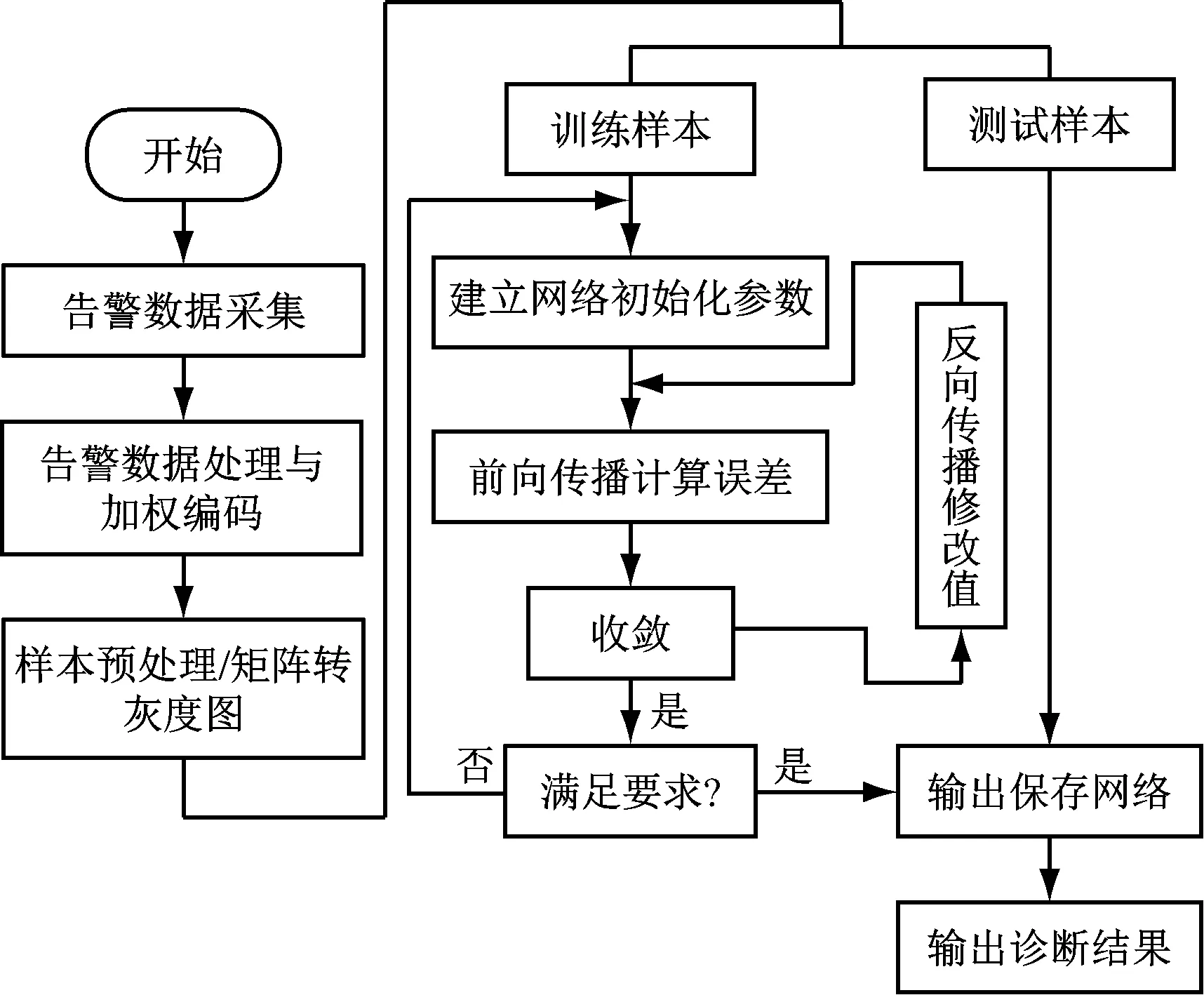
图6 基于CNN的电力通信网故障诊断流程图

步骤1：将采样的告警数据进行预处理和编码得到故障状态矩阵集，并转化为灰度图片。

步骤2：根据输入样本标签和分类要求建立2个CNN网络，每个网络分别包括2个卷积层、2个池化层、1个全连接层、1个输出层。

步骤3：采用截断正态分布法和集成交叉熵函数法分别设置初始参数与定义损失，并采用Adam算法优化器优化训练。

步骤4：将图片通过池化层和全连接层输出，并计算其与真实值的误差a。

步骤5：判断模型是否收敛，若模型未收敛，则进入步骤6，反之，则进入步骤7。

步骤6：将a反向传播到CNN网络各层，并采用BP算法调整各层权值，直到模型收敛。

步骤7：根据损失函数值大小判断CNN网络是否满足要求，若满足则输出最终故障诊断，反之则返回步骤3。

3 仿真实验

3.1 实验环境

电力通信网最重要的组成部分是SDH设备和核心路由器，因此本研究配置的实验环境为由华为技术有限公司提供的11台SDH网络传输机器、4台网管服务器、8台NE40E核心路由器。另外，配置有4台OTN和1台信号发声器以及1套视频会议系统。根据以上设备设施，本研究搭建了如图7所示的电力通信网仿真实验拓扑图。

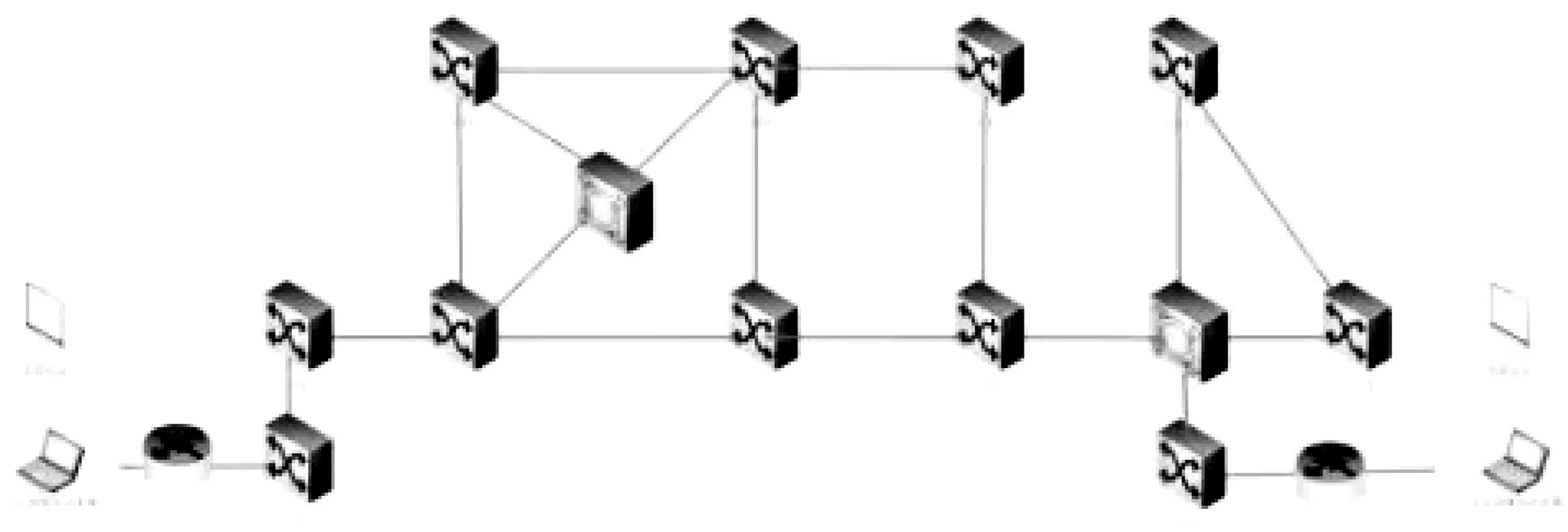
图7 电力通信网仿真测试拓扑图

在SDH配置中，本研究首先进行了物理连接和创建配置网元，然后完成了时钟的同步设置以及保护子网和业务的配置，最后通过上述操作实现了SDH的整体配置。另外，为确保视频会议系统正常运行，本研究配置了5个1兆的视频会议专用业务通道。

核心路由器配置主要是对IP和路由表进行配置。本研究采用串口方式连接路由器的console口，并以命令行的方式进行配置。

3.2 参数调优及实验结果

3.2.1 参数设置

由于神经网络通常存在训练时间长、收敛速度慢的问题，导致模型的训练速度和准确率不高，因此需要对模型参数进行调优处理[10]。通常情况下，参数调优有2种方式，分别是调整与训练过程有关的参数，如学习率、迭代次数、最小批次以及调整与网络结构有关的参数，如网络层数、卷积核个数等。基于本研究中设计的卷积神经网络结构和样本集的特点，本研究主要对与训练过程有关的参数进行了调优。

将模型初始参数迭代次数设置为30次，学习率设置为0.01，最小批次大小设置为128，可得到模型的损失函数如图8所示，模型的准确率如图9所示。

图8 学习率为0.01时模型损失函数

图9 学习率为0.01时模型准确率

由图8、图9可知，模型的损失值在4.02～4.52之间，模型的准确率在0.8%～2.5%之间，且存在剧烈的震荡，均没有呈现出明显的下降或提高。由此可得出，学习率为0.01时，模型没有收敛。这或许是因为学习率过高，故在保持迭代次数和其他参数不变的条件下，调小学习率至0.001，得到模型的损失值如图10所示，准确率如图11所示。

图10 学习率为0.001时模型损失值

图11 学习率为0.001时模型准确率

由图10可知，当迭代次数为20之前，模型的损失值下降速度较快；当迭代次数超过20后，模型的损失值下降速度不明显，其原因或是过度拟合，因此在参数调优中，需要减少迭代次数。由图11可知，当迭代次数为20时，模型的准确率高达98.21%。

综上可知，本研究设计的CNN卷积神经网络结构合理可行，可利用控制变量法对参数进行微调。

3.2.2 参数调优及结果分析

(1)学习率调优结果分析

在最小批次为128，迭代次数为20时，不同学习率的模型结果如表6所示。由表可知，当学习率为[0.000 5,0.004]时，准确率均达到97%以上；当学习率为[0.004,0.005]时，准确率快速下降；当学习率为[0.000 5,0.001]时，准确率提升较小，再降低学习率只会导致训练时间延长，并不会对模型准确率有较大影响，因此可以确定模型最佳学习率应在0.001至0.004之间。

表6 不同学习率的模型准确率

(2)最小批次调优结果分析

在学习率为0.001，迭代次数为20时，不同最小批次大小的模型诊断准确率如表7所示。由表可知，当最小批次大小在128之前，模型的准确率均高于93%；当最小批次大小超过128之后，模型的准确率急剧下降，因此可以确定模型最好的最小批次大小应为128。

表7 不同最小批次大小模型诊断准确率

(3)迭代次数调优结果分析

在学习率为0.001，最小批次大小为128时，不同迭代次数模型的诊断准确率如表8所示。由表可知，当迭代次数为20时，模型的准确率快速提升；当迭代次数大于20后，模型的准确率提升幅度较小，而继续增加迭代次数容易导致过度拟合。因此，综合考虑以上因素，本研究控制迭代次数为20次。

表8 不同迭代次数的模型诊断准确率

3.3 算法比较

为验证卷积神经网络算法的性能，本研究比较了该算法与贝叶斯分类算法的诊断准确率，如图12所示。由图可知，本研究提出的卷积神经网络算法的诊断准确率比贝叶斯分类算法的诊断准确率高6.23%，说明卷积神经网络算法的特征提取能力优于贝叶斯分类算法，具有良好的特征提取能力。

图12 不同算法的故障诊断模型准确率

通过参数调优，本研究设计的卷积神经网络模型的故障诊断准确率达到99.23%，且比贝叶斯分类算法模型的故障诊断准确率高6.23%，说明本研究设计的卷积神经网络模型可有效提取故障和告警之间的特征关系，同时对故障的分类和诊断准确率较高，基本与实际情况相符。

4 总结

综上所述，本研究提出的基于CNN卷积神经网络故障诊断模型结构合理可行，可通过控制变量法对微调参数，进而获得电力通信网故障最佳诊断模型。相较于贝叶斯分类算法模型，该模型对电力通信网的故障诊断准确率提高了6.23%，达到99.23%，基本与实际情况相符。但由于本研究实验场地限制，仅设置了11个网络站点，无法与真实的电力通信网站点相提并论，因此在实际电力通信网络故障诊断中，故障诊断的难度或将大幅度增加。所以，本研究还需在实验环境中增加站点数量，以满足实际电力通信网的需求，使数据集更符合真实情况。