考虑滞后效应与吸附作用的非饱和土SWCC分形模型

李慧鑫，曹文贵，陈 可

(1.湖南大学 土木工程学院，长沙 410082； 2.同济大学 土木工程学院，上海 200092)

1 研究背景

土-水特征曲线(SWCC)是描述土壤基质吸力和饱和度之间关系的曲线，同时也间接描述了其他如土体变形、土体渗透性及土体应力状态等基本规律[1-3],是非饱和土力学中最为基础的本构模型之一。研究结果表明[4-6]:一方面，土-水特征曲线存在显著的滞后特征，在土体干湿循环的过程中，同吸力的土体在脱湿过程中的含水量要比吸湿过程中的含水量高；另一方面，土壤持水不仅与相对较高含水量条件下的毛细作用有关，还会受到较低含水量条件下的吸附作用的影响[7]。因此，建立同时考虑滞后作用与吸附作用的土-水特征曲线模型，可减小其计算结果与土壤实际情况的误差，对于理论研究和实际工程都十分必要。

由于非饱和土的土-水特征曲线测量十分困难且耗时较长，因此，科研人员提出了诸多土-水特征曲线模型用以预测和表征土中的液体流动、应力状态和变形等,如Nimmo[8]、Scott等[9]根据试验曲线提出的经验模型及Mualem[10]、Parlange[11]根据土体含水率分布规律得到的域模型。然而,这些模型仅考虑毛细作用持水，忽略了吸附作用的影响，使得其仅能较好地预测饱和至中等饱和度范围内土壤持水规律，而高估了非饱和土在低饱和度范围的基质吸力。另有部分学者研究了包含吸附作用的土-水特征曲线模型，如Tuller和Or[12]提出了一个考虑低含水量范围内吸附水的土-水特征曲线模型，Peters和Durner[13]也提出了一个加入了吸附作用持水经验函数的土-水特征曲线模型。这些模型很好地反映了低饱和度范围吸附力对土壤持水的作用，但又缺乏对于较高饱和度范围土壤持水存在的滞后效应的考虑，其曲线模型并不完善。可见，当前研究尚未全面考虑滞后效应与吸附膜流对土-水特征曲线模型的影响。因此，本文就这一层面展开研究，建立一个同时考虑吸附作用和滞后效应的非饱和土土-水特征曲线模型，以供工程实际参考。

传统土-水特征曲线模型利用孔隙尺寸参数、热力学理论或结合各类孔隙尺寸分布函数等方法展开研究[14-16]，近年来，能直接将曲线参数与土体微观状态联系起来的分形理论成为研究土-水特征曲线模型的一种新的有效手段。非饱和土体的孔隙尺寸与形状的非均匀分布所造成的瓶颈效应(即“墨水瓶”效应)是导致滞后现象的主要因素之一[17]，而根据研究显示[18-20]，多孔介质的孔隙和颗粒具有明显统计自相似特征，服从分形幂规律，因此分形方法对于研究考虑滞后效应的土-水特征曲线模型极为适用。已有学者利用分形理论对土-水特征曲线滞后模型进行了研究，如Guarracino等[21]和Soldi等[22]基于假设的周期性毛细管细观模型提出了一个考虑滞后效应的非饱和土分形本构模型，杨明辉等[23]在其基础上建立了一个考虑毛细管迂曲度的分形模型。可见，分形理论已经成为研究土体微观分布规律的有效工具。

综上所述，本文从土体渗流特性出发，结合土壤水分运移规律，基于分形理论推导得到了一个同时考虑吸附作用和滞后效应的非饱和土土-水特征曲线模型，以期描述全基质吸力范围的非饱和土持水特性。随后，通过将模型预测结果与试验数据进行对比，验证了该模型的合理性与有效性。

2 土壤持水机理

描述非饱和多孔介质的持水特性，需要明确脱湿与吸湿过程中孔隙水分的运移过程。土壤的持水能力来自毛细作用和吸附作用，这2种物理持水机制作用的吸力范围不同[24]，在持水机制作用下，土壤的水分运移过程可由图1[25]表示。

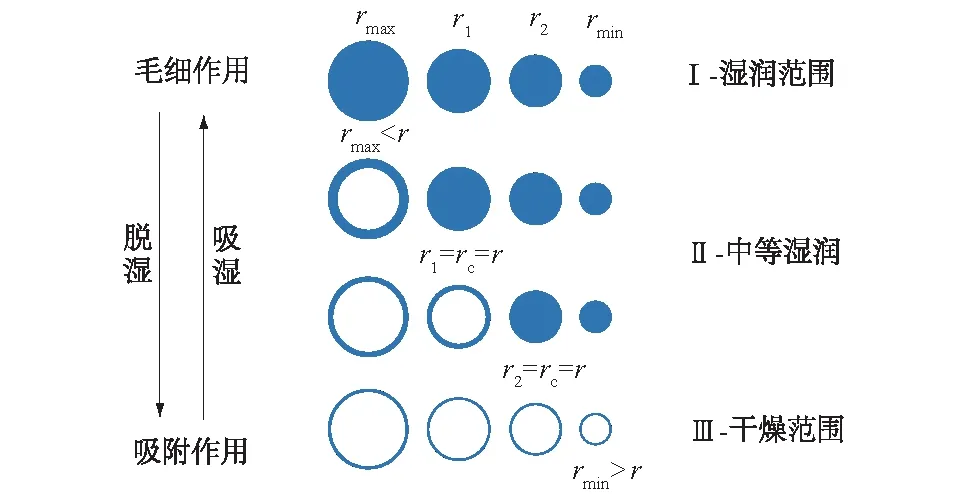
图1 土壤水分运移示意图Fig.1 Schematic diagram of water movement in soil

如图1所示，已知孔隙半径为r，孔隙最大半径与最小半径分别为rmax和rmin，在此区间内分别有孔隙半径r1与r2，在给定的基质吸力下存在一个临界孔隙半径rc，孔径rc的毛细管内表面赋存少量吸附水膜。以土壤脱湿过程为例，在土壤处于饱和状态时，孔隙完全充满毛细水(如图1的状态Ⅰ)，此时土壤持水的主要作用力为毛细作用力；当土壤吸力达到进气值后，开始由饱和状态转向非饱和状态，此时土壤中仍由毛细水填充的较小孔隙与由水膜覆盖的较大孔隙开始持续排水(如图1的状态Ⅱ)，土壤持水的作用力由毛细作用和吸附作用共同提供；随着脱湿过程中吸力进一步提高，土壤含水量逐渐减少，当吸力很高时，土壤孔隙保有极为有限的水分(如图1的状态Ⅲ)，此时液体流动只通过孔隙内表面的吸附薄膜进行，土壤持水主要作用力由吸附作用提供。综上所述，非饱和多孔介质的水分运移过程主要为2个阶段：中等基质吸力范围内由毛细流和吸附膜流共同参与的水分运移阶段和高基质吸力范围内以吸附膜流为核心的水分运移阶段。因此，根据上述水分运移规律不同阶段所表现的不同特征，可以将土-水特征曲线模型分为3部分:①饱和状态下的毛细水组分；②中等饱和度状态下土壤脱湿与吸湿过程中的毛细水与吸附水组分总和；③较低饱和度下的吸附水组分。

3 非饱和土微观孔隙分布分形模型

3.1 建立细观模型

在多孔介质中，分布有大量走向及尺寸大小各异的复杂孔隙，这些孔隙直接影响着多孔介质的变形性质、强度特征以及渗流特性。为了描述全吸力范围的土壤持水特征及滞后特性，本文取一具有代表性的单元圆柱体(Representative Element Volume,REV),假定半径为R，长度为L(见图 2)，将单元土体内的孔隙等效为一束孔径不一且带有孔喉结构的毛细管，这些毛细管服从分形规律。

图2 REV结构示意图Fig.2 Schematic diagram of REV

假设毛细管的半径具有周期性变化，如图 3所示，毛细管的周期长度为λ，半径为r，孔喉的半径用正弦函数来表示，以此表达非饱和土的瓶颈效应。

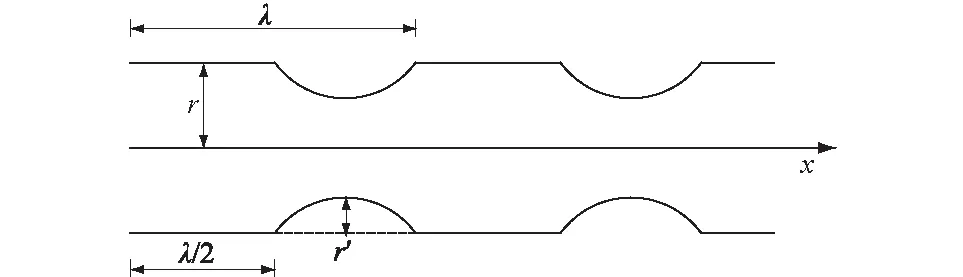
图3 单根毛细管剖面结构Fig.3 Structure of single capillary profile

已知毛细管长度为L，包含i个波长(i=1，2，3,…n)，L=nλ,沿渗流方向可将其孔径r函数描述为

(1)

式中r′为振幅，定义参数a=r′/2r(0≤a<0.5)，则式(2)变为

(2)

当a=0时，毛细管变成半径为r的光滑毛细管，此时的土-水特征曲线上没有瓶颈效应体现。

3.2 用分形方法描述孔隙分布

在3.1节中得到了毛细管的半径r(x)，采用Yu和Li[26]等提出的一种研究多孔介质的孔隙尺度结构的分形方法,即可将毛细管半径与土体饱和度建立起直接联系。假设孔隙半径r从最小值rmin变化到最大值rmax且服从分形定律，有

(3)

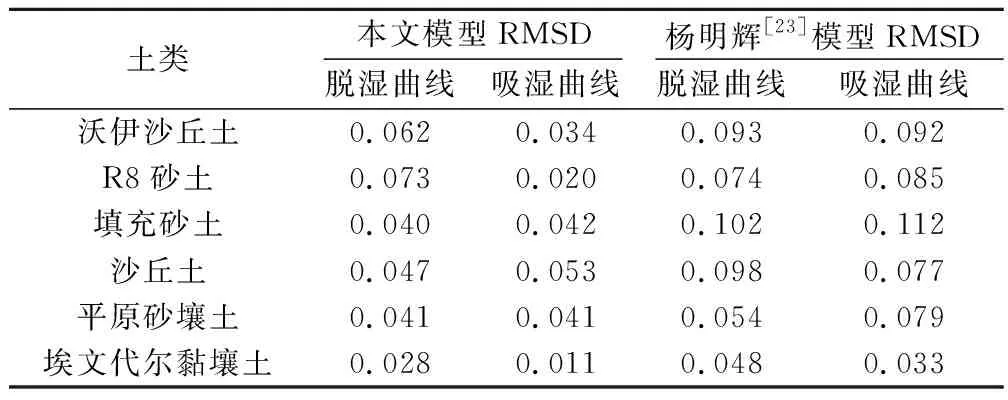
式中：N为单位面积上的毛细管数量；D为分形维数，在二维几何空间中1

通过将式(3)微分，可以得到孔隙尺寸范围在r和r+dr内的孔隙数量为

dN(r)=-DRDr-D-1dr。

(4)

式中-dN(r)>0，其中负号表示孔隙数量随着孔隙半径的增大而减少。

4 土-水特征曲线方程

4.1 细观模型

根据文献[25]所述，毛细管内部的吸附水膜厚度用ω表示，则毛细管内部的吸附水膜比厚度为

δ=ω/r。

(5)

同时，吸附水膜厚度ω与吸力特征半径rc和孔隙半径r有关，因此吸附水膜比厚度δ可用临界孔隙半径rc和孔隙半径r表示为

(6)

式中：α为土壤的吸附强度参数；β为土壤的吸附能力参数。

基于前文所述的毛细管细观模型和土壤孔隙水运移规律，单个毛细管中水的体积可以通过将长度L上的横截面积积分获得，即

(7)

则有

(8)

式中：

(9)

T=1+a2+4a/π 。

(10)

4.1.1 主脱湿曲线模型

为了获得土壤从饱和到干燥过程的主脱湿曲线，假设REV处于饱和状态，在压力水头h下开始排水，孔隙半径在r与r(1-2a)之间波动。可以通过式(11)将孔隙半径与压力水头h联系起来，即

(11)

式中:C=2σcosθ/(ρg)，σ为表面张力，θ为接触角(本文假设为定值)；ρ为孔隙水密度；g为重力加速度。由图1可见，若压力水头h小于临界半径rc所对应的水头，即孔隙半径>rc时，毛细管变为非饱和状态，由此得出，半径r(1-2a)>rc的毛细管开始脱湿，同时半径为rmin到rc/(1-2a)的毛细管状态处于完全饱和状态。

因此，根据饱和度定义有

(12)

(13)

进一步得到

(14)

其中:

(15)

(16)

(17)

(18)

(19)

其中:

(20)

(21)

(22)

(23)

可得

(24)

其中:

(25)

(26)

(27)

其中:

(28)

(29)

整理得到主脱湿曲线为

(30)

4.1.2 主吸湿曲线模型的建立

为了获得土壤从干燥到饱和过程的主吸湿曲线，假设REV处于干燥状态，在压力水头h下开始吸水。由图 1可知，压力水头h大于临界半径rc所对应的水头，即半径r

(31)

(32)

可得

(33)

其中:

(34)

(35)

(36)

其中:

(37)

(38)

同理有

(39)

(40)

可得

(41)

(42)

可得到主吸湿曲线为

(43)

由此得到脱湿与吸湿过程中以饱和度Se与水头高度h之间的关系曲线表示的土-水特征曲线方程，该模型包含孔喉参数a、吸附强度参数α、吸附能力参数β、分形维数D、最小水头高度hmin及最大水头高度hmax6个参数。

4.2 数据验证

4.2.1 模型验证

通过对比本文提出的土-水特征曲线模型的预测曲线与文献[27]中的试验数据来验证本文模型的合理性,并利用最小均方偏差(RMSD)评价预测结果,RMSD可表示为

表1 模型参数和最大/最小吸力水头与RMSDTable 1 Fitting values of model parameters and maximum and minimum suction head and RMSD

图4 本文模型与试验数据对比Fig.4 Comparison of SWCC between modelling and experimental data

从图4可见，各组试验数据与本文模型吻合良好。本文选用的6组试验数据的吸力水头最大值均为 1×105m，可以很好地反映非饱和土在全基质吸力范围的土-水特征曲线的持水性质，总的来看，毛细作用主导时滞后效应明显，在吸附膜流传导中不存在滞后现象。

对比土类曲线发现，砂质土壤对于较高饱和度下毛细水的滞后持水性与低饱和度下吸附水持水性的拟合效果最为理想。对比表1土类可知，砂土的吸附能力低于黏质土壤，毛细作用持水范围小于黏质土壤，吸力水头更低。这是因为黏质土壤中亲水矿物含量更高，土颗粒的比表面积更大，且土颗粒与平均孔隙半径都较小，所以具有更高的吸力水头，从而增大了它的毛细作用持水范围。

对比图4中的(a)—(f)可发现，在低饱和度范围下，黏质土壤孔隙中的吸附水含量比砂质土壤更高，且曲线更为和缓。这些结果出现的原因在于在排水过程中，砂质土壤孔隙较大排水较快使其曲线走势更为陡峭，黏质土壤吸附作用特征更为显著是由于其孔隙较小，在排水过程中赋存了更多的水分。

另一方面，由图4可知，与脱湿曲线相比，吸湿曲线的模型计算值与试验数据更加吻合，这是由于本文的SWCC曲线方程为分段函数，而孔喉参数a的存在使吸湿过程和脱湿过程无法完全同步，在拟合过程中吸湿曲线先于脱湿曲线达到下一阶段以满足相同的边界条件，因此脱湿曲线末尾阶段的模型计算结果与试验数据略微有一定误差。脱湿曲线由拟合试验数据得到的参数a、D、α、β决定，吸湿曲线由理论计算获得。因此，可以通过拟合脱湿曲线试验数据确定参数，然后使用式(30)和式(43)实现从脱湿曲线预测吸湿曲线。

4.2.2 模型对比

在4.2.1节已通过与试验数据的对比验证了本文模型的可行性，本小节将通过与其他模型对比，进一步评价本文模型的优越性。杨明辉等[23]基于分形理论提出了一个非饱和土土-水特征曲线的理论分形模型：

(45)

式(45)为脱湿曲线函数表达式，式(46)为吸湿曲线函数表达式。其中，a为孔喉半径参数，DT与Df为分形维数，其余参数物理意义与本文模型相同。表2给出了2个模型拟合6组试验数据的RMSD值，图5为2个模型计算Se值与实测Se值的散点图，显示了本文模型(式(30)、式(43))与杨明辉等[23]所提出的土-水特征曲线分形模型(式(45)、式(46))的对比情况。

表2 2个SWCC分形模型的RMSDTable 2 RMSD of two SWCC models

图5 本文模型与杨明辉[23]模型对比Fig.5 Comparison between the model in this paper and Yang’s model[23]

从表3可以看出，与杨明辉等[23]提出的SWCC分形模型相比，对于每一种土壤本文所提出的模型都表现更好。2个模型之间的差异可以清楚地显示为相对饱和度Se计算值与实测值的散点图，如图5所示。图5中散点图的横坐标代表6组试验数据的实测Se，纵坐标代表利用本文模型与杨明辉等[23]模型计算得到的Se，实线代表实测值与计算值相等的情况，数据点越接近实线则说明模型的拟合效果越好。由图5可知，2个模型拟合效果较为良好，但本文所提出的模型计算结果与试验数据更为接近。

2个模型的总体性能可以通过RMSD的平均值(aveRMSD)来反映，本文模型脱湿曲线(式(31))aveRMSD为0.221，杨明辉等[23]提出的分形模型脱湿曲线(式(46))aveRMSD为0.279，本文模型吸湿曲线(式(44))aveRMSD为0.183，杨明辉等[23]提出的分形模型吸湿曲线(式(47))aveRMSD为0.283。由于杨明辉等[23]提出的SWCC曲线分形模型仅考虑了毛细水组分而忽略了吸附水组分，因此其相对饱和度计算值与试验实测值误差较大，特别是在低饱和度范围，其误差更为明显。而本文所提出的SWCC曲线分形模型Se计算值非常接近试验实测值，相对饱和度Se计算值与实测值的数据集显示出更好的线性关系，可见本文所提出的SWCC曲线分形模型具有明显的优越性。

5 结 论

本文基于分形理论，将土壤孔隙等效为一束具有周期性孔喉且其孔径分布服从分形定律的毛细管，结合土壤水分运移规律对非饱和土不同水力过程的土-水特征曲线的滞后效应以及持水机制进行分析，得出以下结论：

(1)提出了一种考虑吸附膜流的多孔介质不饱和流动水力特性的估算理论分形模型，并得到了包含孔喉半径参数a、分形维数D、吸附强度参数α、吸附能力参数β和最小、最大水头高度(hmin、hmax)6个参数的土-水特征曲线函数表达式，其可通过拟合脱湿曲线获得模型参数，然后用于预测吸湿曲线。通过与试验数据和其他研究成果的对比，证明了该模型的合理性，同时该模型具有明显优越性，可有效反映土-水特征曲线的滞后效应和非饱和土在低饱和度范围内的持水特性。

(2)根据持水机制将土壤中孔隙水运移过程分为分别以毛细作用与吸附作用共同主导和以吸附作用为核心的2个阶段绘制曲线，从非饱和土土-水特征曲线上反映出毛细管传导中存在滞后现象，但在吸附膜流传导中不存在滞后现象。

(3)在利用不同种类的土壤试验数据对该模型进行验证时，通过对比不同类型土壤的持水特征参数，发现砂质土壤的吸附能力普遍低于黏质土壤，毛细作用持水范围小于黏质土壤，在低饱和度范围下的残余水含量更低。