磁力吸附爬柱机器人磁吸附单元磁路设计分析
2022-07-12王战中杜启鑫张明亮
王战中 赵 童 杜启鑫 张明亮
1(石家庄铁道大学机械工程学院 河北 石家庄 050043) 2(张家口职业技术学院 河北 张家口 076450)
0 引 言
磁力吸附爬柱机器人属于特种机器人的范围[1],在极限作业领域特种机器人有着不可替代的作用[2],尤其是在高铁站雨棚金属支柱表面检测与维护方面拥有非常大的潜力,磁力吸附爬柱机器人可以代替人类在垂直或陡峭的金属圆柱壁面上作业,既能够高效地检测出金属支柱内部腐蚀情况,又能保障工作人员的安全,减少作业周期,提高工作效率[3]。
在磁力吸附爬柱机器人设计方面,保证磁吸附力的同时,减小磁吸附装置的体积与重量是尤为重要的。而永磁磁路设计对于磁吸附力的大小有很大的影响。桂仲成等[4]提出一种按照磁吸附装置的自身重量与可提供的磁吸附力的比值对磁吸附装置进行优化设计,并将永磁铁块按照相邻磁极极性互不相同的排布方式进行分析,运用有限元方法对几种排布方式建立模型,最终得出在气隙为6.2 mm时磁吸附力能达到2 400 N的结果。薛珊等[5]通过与传统磁路(充磁方向为径向,永磁铁间采用隔磁材料隔开)对比,提出一种新型的磁吸附单元模型(充磁方向为轴向,上方采用隔磁材料,永磁铁间采用导磁材料隔开),并运用Ansoft Maxwell模块对其进行仿真分析,最后得出新型磁吸附单元的磁利用率比较高的结论。陈勇等[6]提出一种新型变磁力吸附单元机构,磁吸附单元是由Halbach永磁阵列和软铁组成,克服了Halbach两端的漏磁问题,运用ANSYS软件对其进行优化设计,并与传统H阵列模型比较,最终得出的新型吸附单元永磁利用率高的结果。袁硕等[7]提出了一种基于Halbach阵列的永磁吸附单元,新型吸附单元充磁方式为水平与垂直相结合,上部与端部都采用导磁材料,并运用Ansoft Maxwell二维模块对其进行仿真分析,得到了影响磁吸附力的主要因素为垂直充磁的永磁铁长度与端部轭铁厚度。潘柏松等[8]基于Halbach环形阵列理论提出了一种新型磁轮吸附单元的拓扑结构,并运用有限元方法对磁轮轭铁厚度、偶数极对数、永磁单元的不同体积配比等因素分析了对磁吸附力的影响。宋伟等[9]引入了磁质比来对磁吸附装置进行优化设计,并利用Ansoft MaXwell软件对不同结构参数的吸附力和磁质比进行计算,最后得出增大永磁铁宽度可以提高磁质比的结论。
对于磁力吸附爬柱机器人的磁吸附装置的磁路设计,目前文献大都是基于单层Halbach永磁阵列进行研究,而忽略了双层Halbach永磁阵列对磁吸附力的影响。因此,为了在能够保证磁吸附力的同时,使机器人质量达到最小,磁吸附装置所占空间最小,本文将1块大小为2 cm×4 cm×1 cm的永磁铁沿厚度方向平分,上部永磁铁磁化方向是垂直向下(N-S极),下部永磁铁按长度方向分别平分为5片、10片、15片、20片、25片、30片、35片,并采用Halbach阵列排布,上下形成对顶式模型进行仿真研究,以便找出最佳的永磁铁块厚度及最佳的双层Halbach永磁阵列模型。
1 三维模型建立与磁路设计
Halbach理论指的是将不同磁化方向的永磁铁按照一定规则排列,会得到一边显著增强,而另一边显著减弱的磁场。本文基于Halbach永磁铁阵列理论,将一块长×宽×高为2 cm×4 cm×1 cm的永磁铁沿高度方向平分成上下两块。上方部分从上到下磁化为N-S极,下方部分沿长度方向分别平分成5片(每片4 mm)、10片(每片2 mm)、15片(每片1.3 mm)、20片(每片1 mm)、25片(每片0.8 mm)、30片(每片0.67 mm)、35片(每片0.57 mm),并依次按照Halbach阵列连续排列,构成7种Halbach阵列模型。然后分别将这7种模型导入到MaxWell软件中进行仿真实验研究。磁路设计模型如图1所示,其中箭头方向表示永磁铁磁化方向,下方为不同厚度的永磁铁块Halbach排列方式。
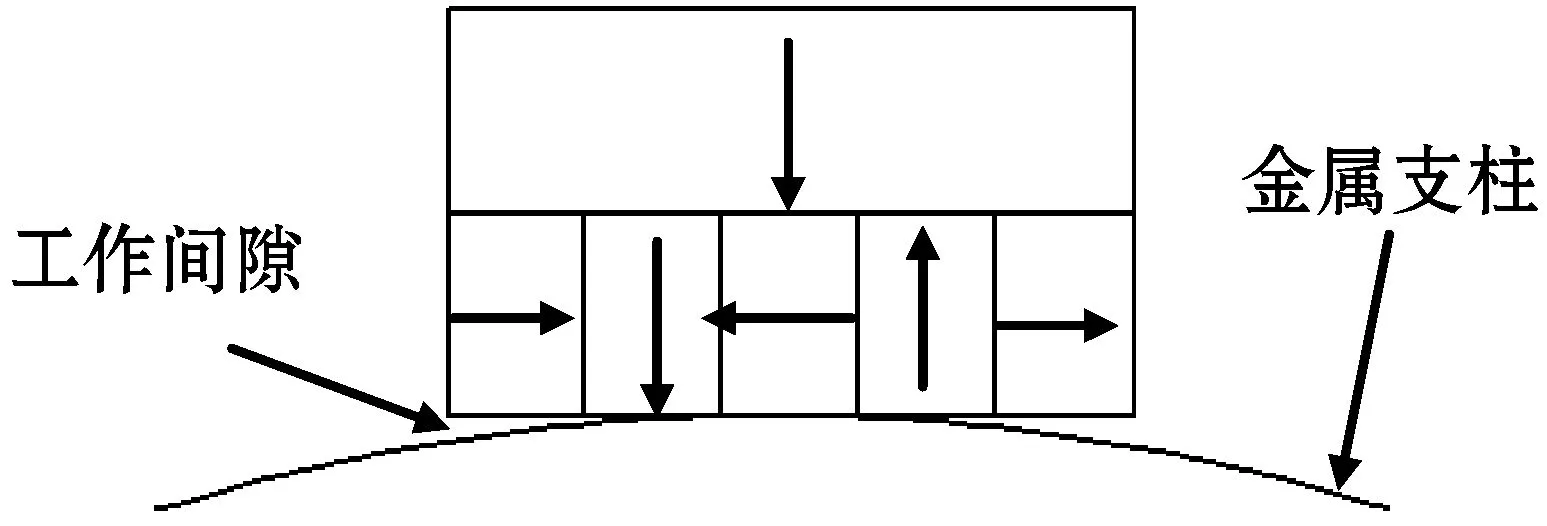
(a) 下方为5片永磁铁
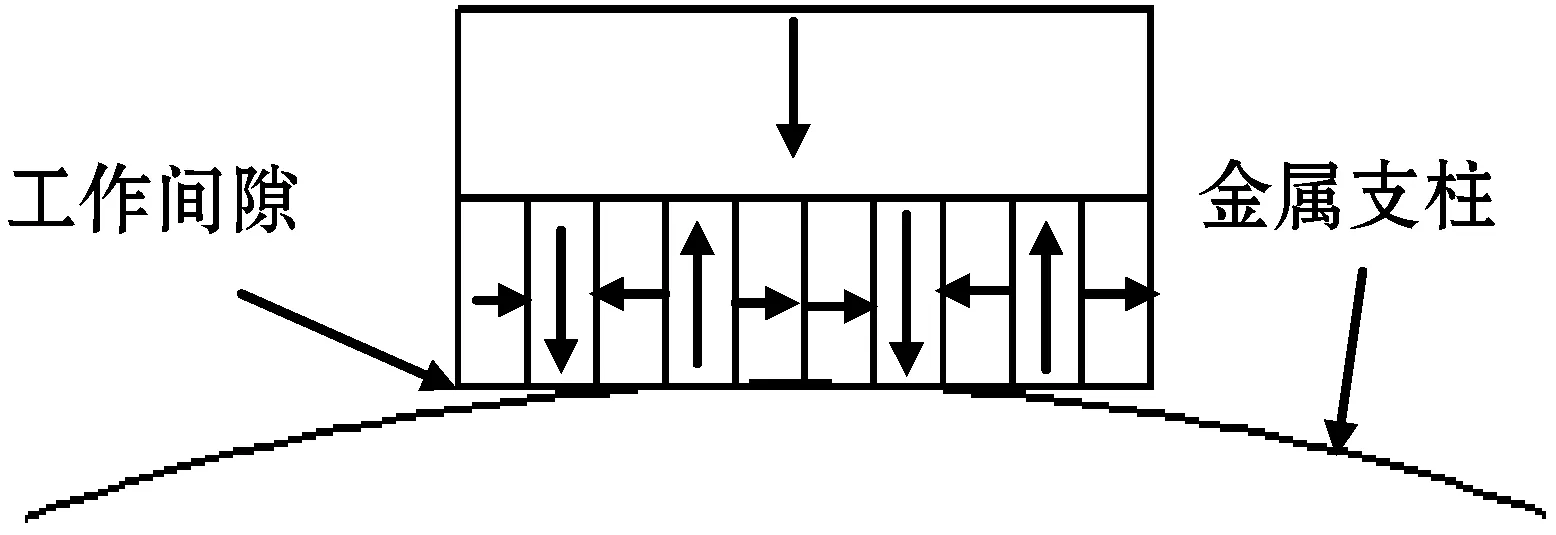
(b) 下方为10片永磁铁

(c) 下方为15片永磁铁

(d) 下方为20片永磁铁
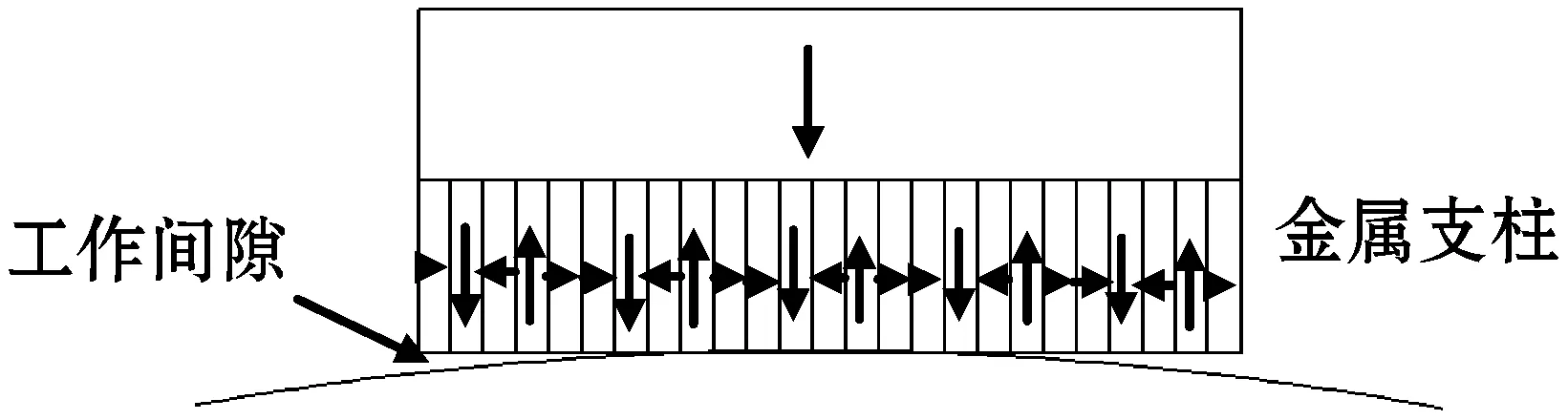
(e) 下方为25片永磁铁
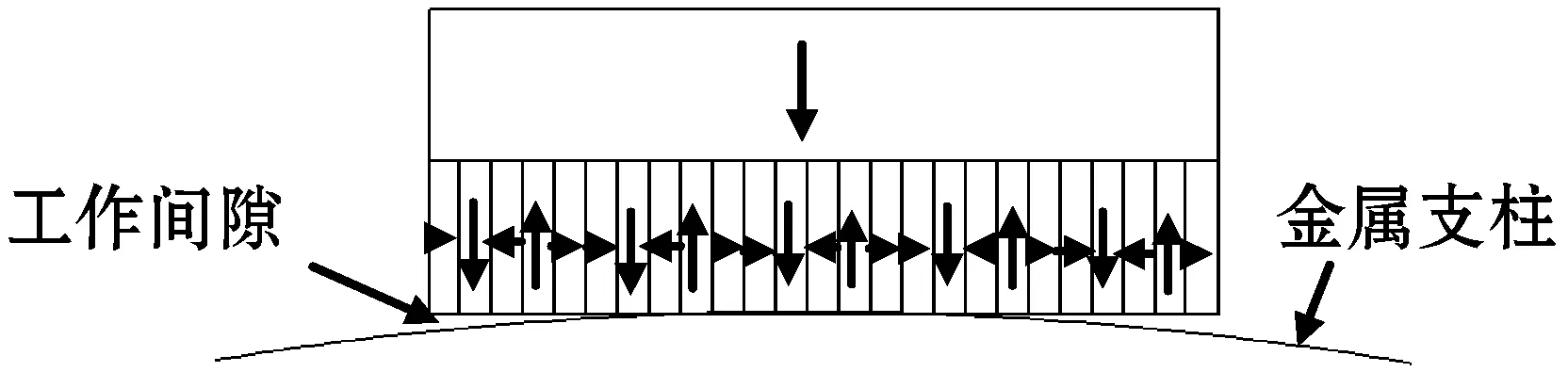
(f) 下方为30片永磁铁
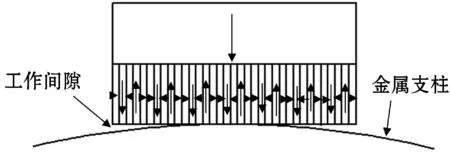
(g) 下方为35片永磁铁图1 基于Halbach阵列磁路设计模型图
2 有限元分析
2.1 数学模型
以图1(a)为例来推导数学模型。
(1) 单块永磁体建模。
根据毕奥萨伐尔定律可得:
(1)
式中:dB表示磁感应强度微量;I表示源电流;dl是源电流的微小线元素;r为电流元指向待求场点的单位向量;μ0为真空导磁率。
图2是一块永磁铁示意图,长、宽、高分别为a、b、c,D′B′、B′A′、A′C′和C′D′分别是DEFB、BFGA、AGHC和CHED面上的微面,p1(x1,y1,z1)、p2(x2,y2,z2)、p3(x3,y3,y3)和p4(x4,y4,z4)分别是微面上的任意一点,这4个微面上的电流在空间任意点p(x,y,z)处产生的磁感应强度为:
① 微面D′B′:
(2)
(3)
dBZ1=0
(4)
② 微面B′A′:
dBX2=0
(5)
(6)
(7)
③ 微面A′C′:
(8)
(9)
dBZ3=0
(10)
④ 微面C′D′:
dBX4=0
(11)
(12)
(13)
dBX=dBX1+dBX2+dBX3+dBX4=

(14)
dBY=dBY1+dBY2+dBY3+dBY4=

(15)
dBZ=dBZ1+dBZ2+dBZ3+dBZ4=
(16)

图2 一块永磁铁示意图
图2中的永磁体产生的磁感应强度为:
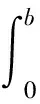
(17)
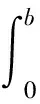
(18)
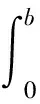

(19)
图3所示为下方为5片永磁铁模型编号图,磁化方向不同、位置不同的永磁体,可通过坐标变换得出其磁感应强度[10]。图3中①号永磁铁可由图2中的永磁铁绕X轴逆时针旋转90°得到,②号永磁铁可由图3中的永磁铁绕Z轴逆时针旋转90°得到,③号永磁铁即为①号永磁铁,④号永磁铁可由②号永磁铁对称得到,⑤号永磁铁可由②号永磁铁绕Y轴逆时针旋转90°得到,⑥号永磁铁可由②号永磁铁平移得到。不同尺寸的永磁铁只需代入不同的长、宽、高a、b、c即可。
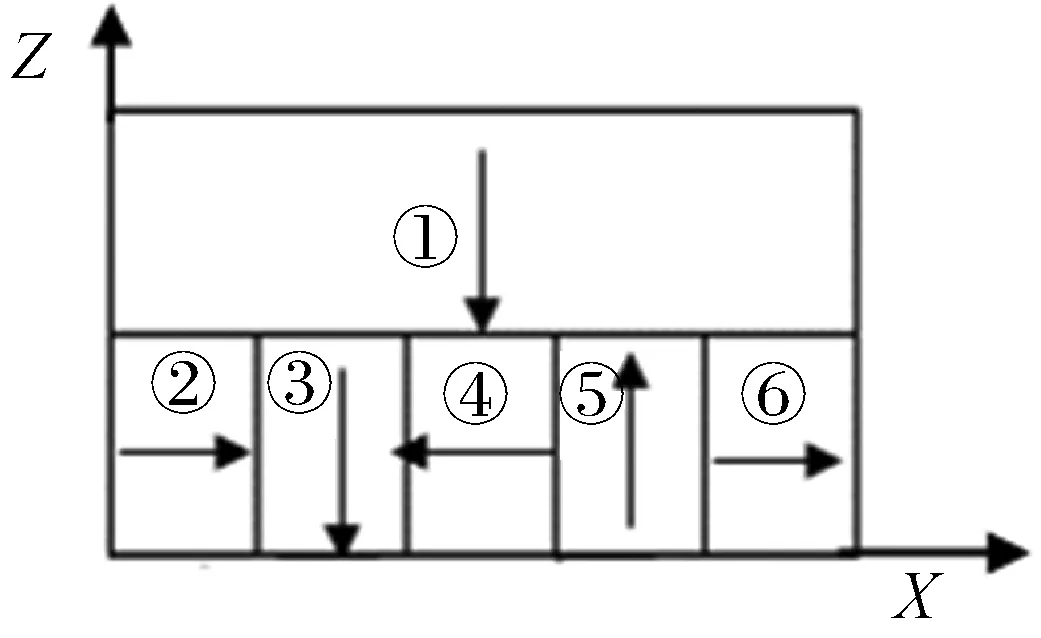
图3 下方为5片永磁铁模型编号图
对这6个永磁铁的磁感应强度求和,可得下方5片永磁铁的磁感应强度为[10]:
(20)
式中:m=X、Y、Z,j=1、2、3、4、5、6。
磁吸附力可表示为[11]:
(21)
式中:B表示永磁铁的磁感应强度;a为永磁铁长度;b为永磁铁宽度;μ0为真空导磁率;k为周波数;d为永磁铁厚度;L为工作间隙(永磁铁到壁面的间距)。
将式(20)代入式(21)即可求出该模型所受的磁吸附力。
2.2 材料确定
该模型中涉及到的研究对象有永磁铁、金属支柱壁面、工作间隙介质与空气,需要分别指定材料属性。永磁铁选为Ansoft Maxwell材料库中牌号为35的钕铁硼材料,性能如表1所示。金属支柱的材料选为纯铁(Iron)。设置工作间隙介质与空气的磁导率μr=1.0。

表1 钕铁硼N35参数
2.3 ANSYS求解分析
利用三维建模软件建立磁吸附装置模型并导入到Ansoft Maxwell中进行磁吸附力仿真实验分析。在Maxwell软件中有二维与三维两种模块,其中:二维模块仅适用于分析平面中的磁场模型,因此具有一定的局限性;三维模块可用于解决空间问题。而雨棚金属支柱属于空间曲面,因此永磁铁块的布局及磁路也属于空间结构,因此本文采用三维模块进行有限元分析。
首先采用1块磁化方向为沿Y轴负方向的永磁铁(2 cm×4 cm×1 cm)在Ansoft Maxwell软件中进行仿真分析,工作间隙设置为0 mm,网格长度为0.9 mm,计算出的磁吸附力为166.17 N。其模型如图4(a)所示。网格划分如图4(b)所示。磁感应云图与磁吸附力如图4(c)所示。

(a) 块普通永磁铁模型
(b) 网格划分
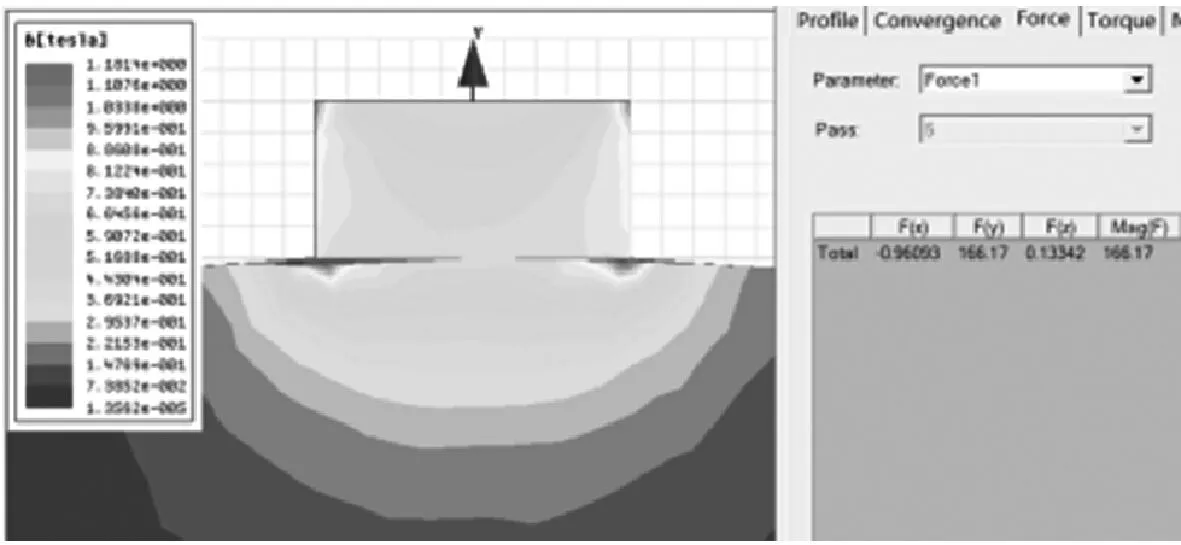
(c) 磁感应强度云图与磁吸附力图4 一块普通永磁铁模型、网格划分及磁感应强度云图
其次,按照图1所示磁路设计方案建立7种三维模型,并导入到Ansoft Maxwell软件中进行仿真分析。7种仿真模型中,永磁铁材料、工作间隙、磁铁总体尺寸及介质与空气磁导率等都与一块普通磁铁仿真(图4)情况下是一样的,因此,影响磁吸附力的主要因素就是下方永磁铁块的薄厚程度与Halbach阵列的数量。此次仿真实验的目的在于找出随着下方永磁铁变薄以及Halbach阵列数量的增加,磁吸附力的变化规律并最终确定最佳磁吸附单元。图5所示为磁路设计方案A的仿真模型及磁感应强度云图,图6-图11为其余6种磁路设计方案的仿真模型、网格划分及磁感应强度云图。将仿真计算出的磁吸附力列表如表2所示,并用Origin软件将表中数据绘制成磁吸附力随永磁铁数量的变化曲线图,如图12所示。

(a) 方案A三维模型
(b) 网格划分(网格长度为0.7 mm)
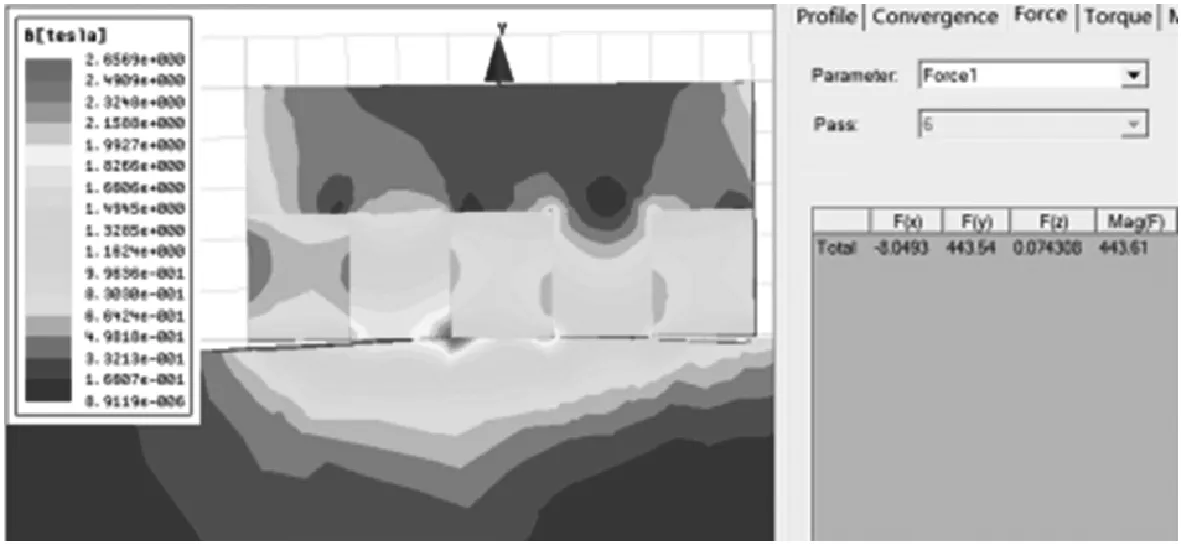
(c) 磁感应强度云图及磁吸附力图5 方案A的仿真模型、网格划分及磁感应强度云图
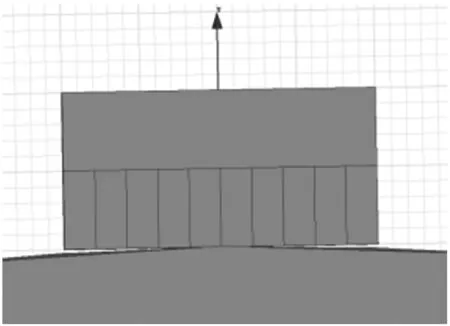
(a) 方案B三维模型

(b) 网格划分(网格长度为0.5 mm)

(c) 磁感应强度云图及磁吸附力图6 方案B的仿真模型、网格划分及磁感应强度云图

(a) 方案C三维模型

(b) 网格划分(网格长度为0.4 mm)

(c) 磁感应云图及磁吸附力图7 方案C的仿真模型、网格划分及磁感应强度云图
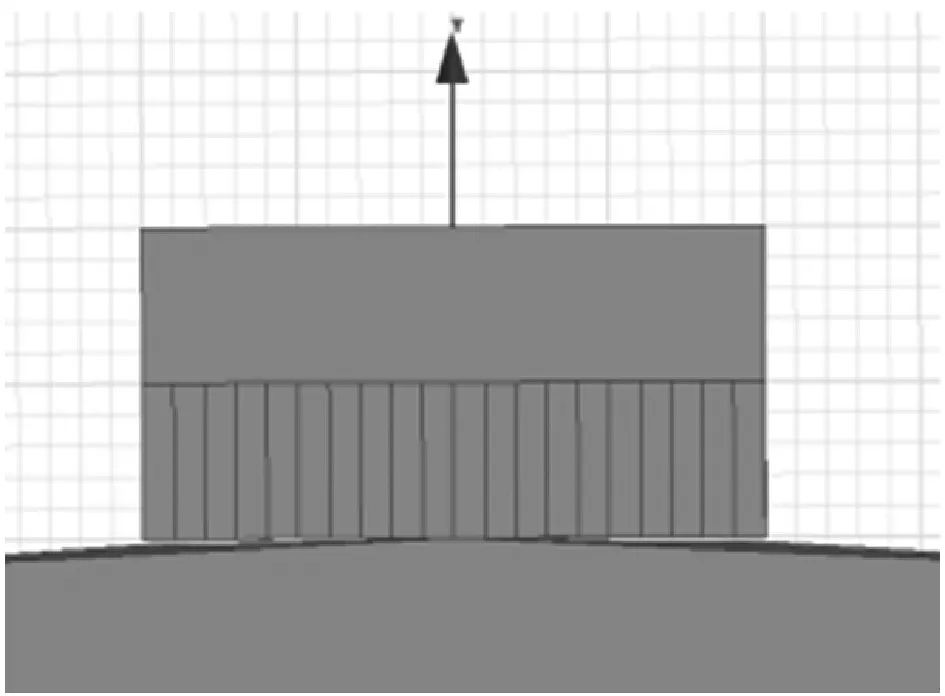
(a) 方案D三维模型

(b) 网格划分(网格长度为0.3 mm)
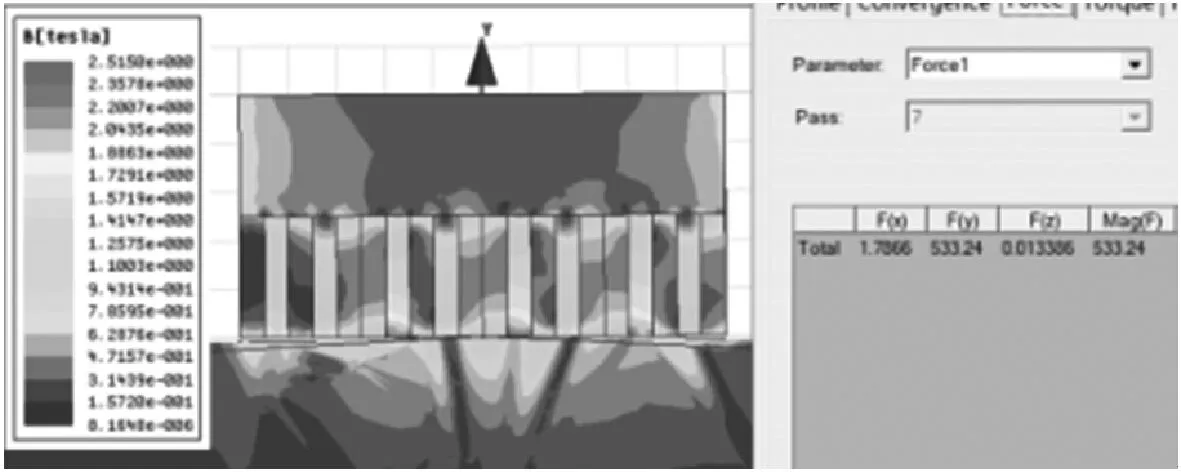
(c) 磁感应强度云图及磁吸附力图8 方案D的仿真模型、网格划分及磁感应强度云图

(a) 方案E三维模型
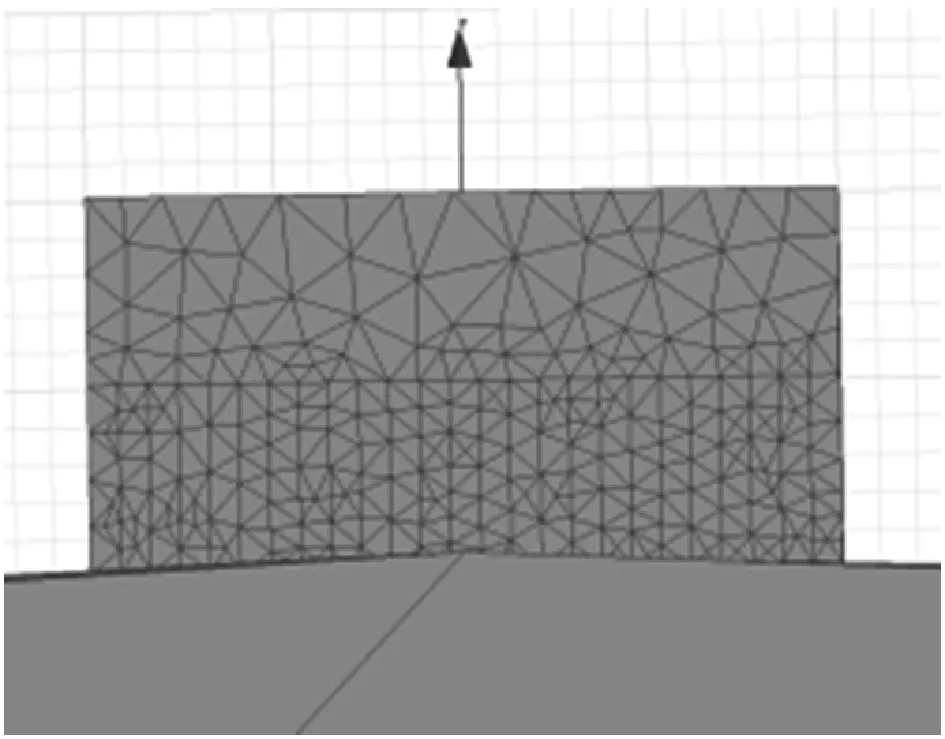
(b) 网格划分(网格长度为0.3 mm)

(c) 磁感应强度云图与磁吸附力图9 方案E的仿真模型、网格划分及磁感应强度云图
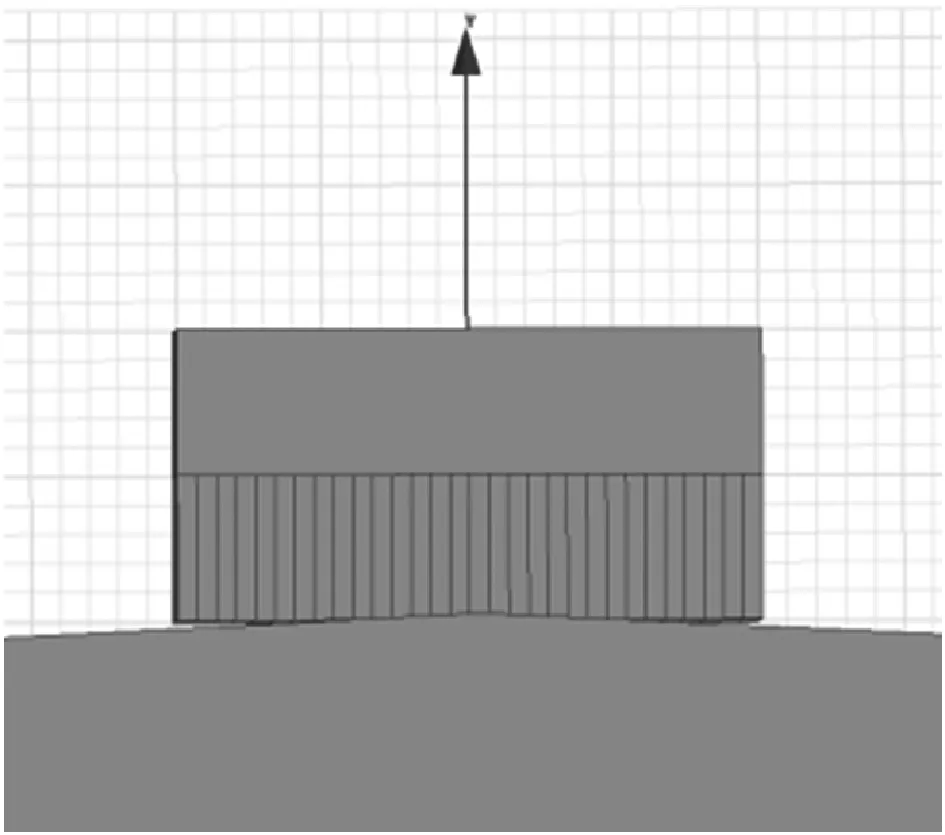
(a) 方案F三维模型
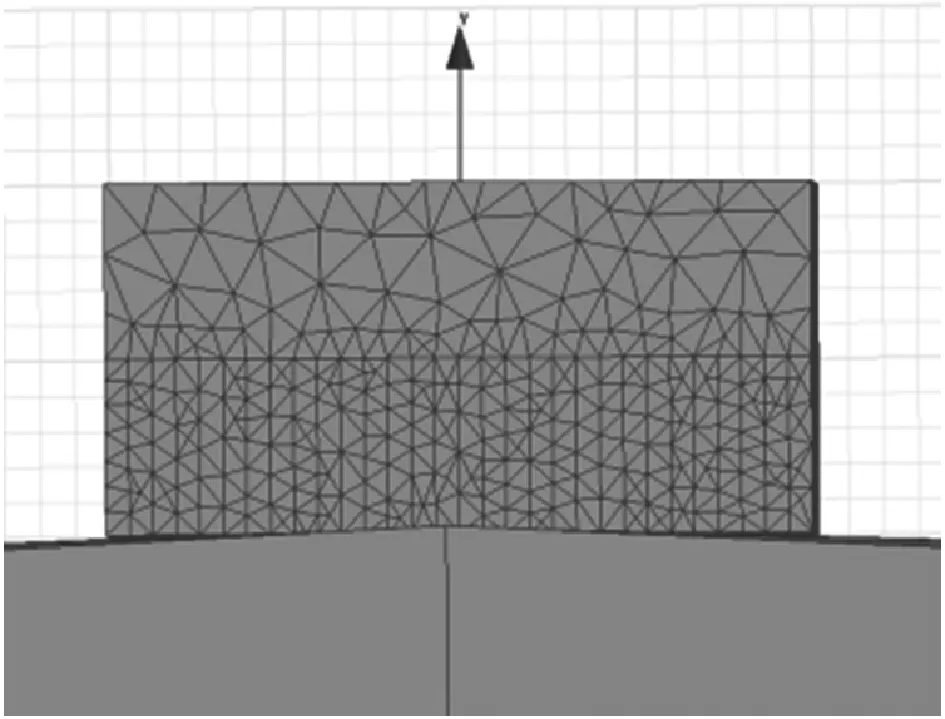
(b) 网格划分(网格长度为0.2 mm)

(c) 磁感应强度云图和磁吸附力图10 方案F的仿真模型、网格划分及磁感应强度云图

(a) 方案G三维模型

(b) 网格划分(网格长度为0.1 mm)
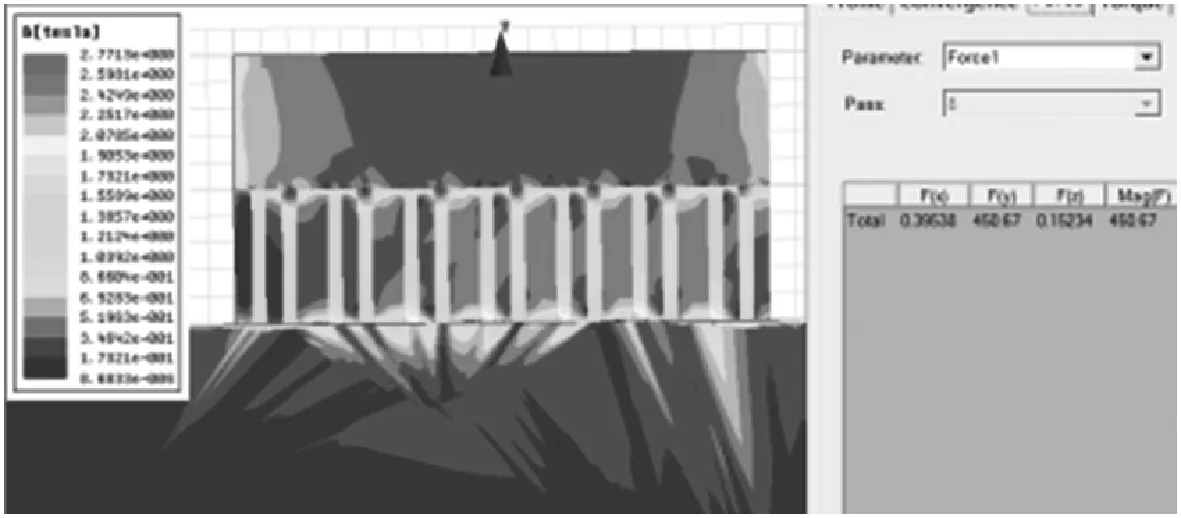
(c) 磁感应强度云图和磁吸附力图11 方案G的仿真模型、网格划分及磁感应强度云图
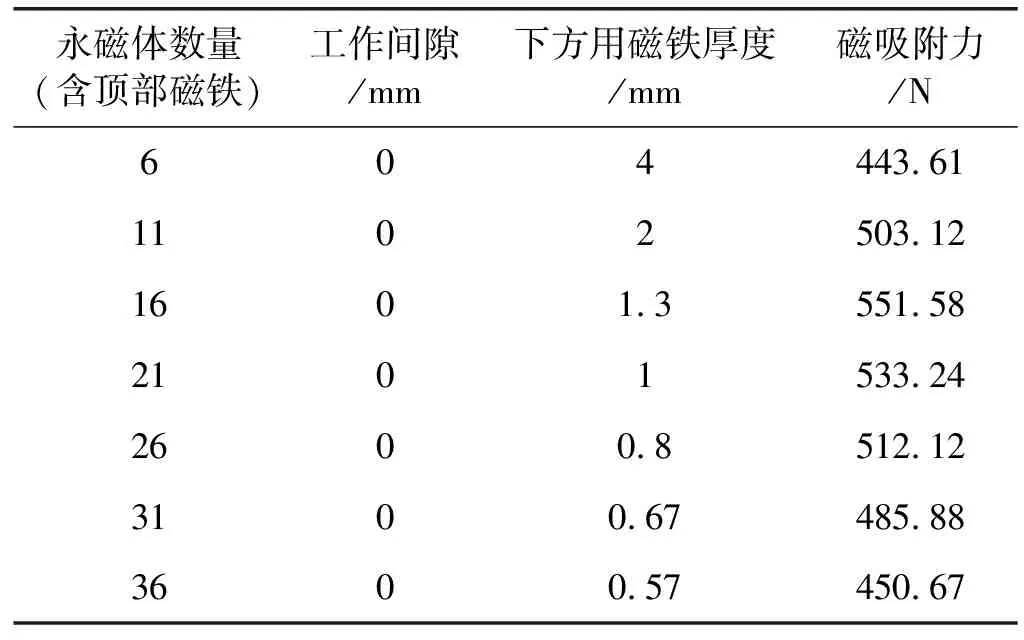
表2 每种永磁体数量对应的磁吸附力
由表2可看出,在吸附单元总体积不变的情况下,7种模型的磁吸附力都达到了440 N以上,也就是说,采用双层上下对顶式磁路设计的磁吸附单元模型所产生的磁吸附力至少是1块普通永磁铁块产生的磁吸附力的约3.5倍。
从图12中还可以看出,随着永磁铁块厚度的变薄以及Halbach阵列数量逐渐增多,磁吸附力并不是一直增大的,而是随着永磁铁数量的增加与Halbach阵列的数量增加,磁吸附力先增大后减小,呈一种近似抛物线的变化趋势。当永磁铁数量为16块(上方1块整的,下方15片薄片),且下方为三个Halbach阵列连续排列时,磁吸附力达到最大,为551.58 N。由此可以得出结论:相比于选用普通永磁铁块(2 cm×4 cm×1 cm)作为磁吸附单元,选用下方为15片薄片永磁铁块且排列成三个连续Halbach阵列的排列模型作为磁吸附单元,磁力吸附爬柱机器人的磁吸附装置的体积和重量会明显减小,从而能够降低磁力吸附爬柱机器人的体积和重量。
3 结 语
(1) 针对在能够保证磁吸附力的同时,使机器人自身重量最小,磁吸附装置所占空间最小的目标,基于Halbach布局原理,提出双层上下对顶式排布方式并进行仿真分析,仿真实验结果证实双层上下对顶式排布的磁吸附单元的磁吸附力至少是同等体积的1块普通永磁铁所产生的磁吸附力的3.5倍以上。
(2) 运用Ansoft软件对7种磁吸附单元进行仿真分析,得出随着下方永磁铁块厚度的减小和Halbach阵列数量的增多,磁吸附力的变化呈一种近似抛物线的变化趋势。
(3) 双层上下对顶式排布中,当下方永磁铁块为15片时,且呈三个Halbach阵列连续布局时,磁吸附力达到最大,为551.58 N。采用这种磁吸附单元模型,可以有效减小磁力吸附装置的体积并显著降低磁力爬柱机器人的重量。
