气体扩散层孔隙率梯度对质子交换膜燃料电池水管理的影响

程植源，周荣良，李嘉颀，纪嘉树，闫伟

山东大学 能源与动力工程学院，山东 济南 250061

0 引言

质子交换膜燃料电池(proton exchange membrane fuel cell, PEMFC)具有工作温度低、零污染、无腐蚀等优点，在新能源汽车领域，特别是零排放交通运输领域一直保持相当的研究热度[1]。膜电极(membrane electrode assembly，MEA)由质子交换膜、催化层与气体扩散层(gas diffusion layer, GDL)构成，是PEMFC的核心部件，其中，GDL由多孔材料制成，具有导电性，能够收集电流、传输气体和排水[2]。PEMFC在运行时产生的液态水，可能会使扩散层出现“水淹”现象，阻碍气体到达反应位点，减小催化剂的有效活性面积，同时使燃料电池的活化损耗和浓差损耗增大[3]，因此，对GDL进行优化设计是提升PEMFC性能的重要途径。研究表明，孔隙率的变化对GDL的性能具有决定性影响。刘洪建[4]在典型工况下研究了GDL在不同孔隙率下液态水的分布情况，结果表明，随着孔隙率减小，流道下方的水饱和度呈直线增长，肋下则先增大后减小；李姣等[5]通过二维模拟研究了扩散层孔径分布的变化对电池性能的影响；何玉松等[6]利用具有多反射固体边界的多弛豫时间格子玻尔兹曼方法模拟了微扩散层内的单相流动，并分析了孔隙率对微扩散层孔隙结构和渗透率的影响；张宁等[7]研究了阴极扩散层孔隙率单一分布、线性梯度分布、随机分布等情况，得出孔隙率对阴极氧气传输和水管理的影响。

GDL作为气体和液体的传输通道，孔隙率是决定GDL性能的关键参数，孔隙率的变化对燃料电池的水管理具有重要影响[8]。本文中基于COMSOL Multiphysics软件建立PEMFC三维模型，并通过改变GDL的梯度分布结构，研究孔隙率的梯度结构对燃料电池内部排水性能和电性能的影响。

1 模型建立

1.1 模型假设

研究时遵循以下假设： 1)PEMFC在等温、稳态下工作； 2)GDL和催化层为均质多孔介质，且不同孔隙率梯度分布的GDL内每层皆为均质多孔介质； 3)反应气体均为理想气体； 4)反应气体在流道中以层流流动[9-11]。

1.2 几何模型

采用某燃料电池制造公司提供的几何模型，为了计算简便，选取其中2条具有代表性的流道进行研究。燃料电池的具体结构参数如表1所示，PEMFC整体结构如图1所示。

图1 燃料电池整体结构示意图

表1 燃料电池的主要参数

1.3 控制方程

H2和O2的电化学反应使PEMFC产生电能，常用电化学方程表达。反应过程存在电子、质子、H2、O2和水的输运过程，在电池内质量、动量、能量和组分均守恒。

质量守恒方程[12]为：

(1)

式中：ε为孔隙率；ρ为各相密度，kg/m3；u为各相速度，m/s；t为时间，s。

动量守恒方程[12]为：

(2)

式中：μ为黏度，kg/(m·s)；p为压力，Pa；SN为动量源项，N/m3。

能量守恒方程[12]为：

(3)

式中：cp为定压比热，J/(kg·K)；T为温度，K；keff为有效导热效率，W/(m·K)；SQ为能量源项，W/m3。

组分守恒方程[12]为：

(4)

ck=ρxk，

(5)

式中：ck为各气体组分密度，kg/m3；Dkeff为扩散系数，m2/s；Sk为源项；xk为气体组分的质量分数；k为组分，当k=a时代表阳极，k=c时表示阴极。

一般使用Butler-Volmer方程描述催化层发生的化学反应，电化学方程[12]为：

(6)

式中：ηk为过电位，V；rk为浓度指数；αk为传递系数；jk,ref为参考交换电流密度，A/m2；Ck为气体摩尔浓度，kmol/m3；Ck,ref为参考摩尔浓度，kmol/m3；k=a时，Ck为氢气摩尔浓度，Ck,ref为氢气参考摩尔浓度，k=c时，Ck为氧气摩尔浓度，Ck,ref为氧气参考摩尔浓度；F为法拉第常数，C/mol；R为气体常数，J/(mol·K)。

1.4 仿真设计与模型检验

为了探究GDL的孔隙率对电池排水性能的影响，首先对单一孔隙率的GDL进行仿真，不同电池电压和GDL孔隙率下对应的最大水摩尔分数和平均水摩尔分数如表2、3所示。由表2、3可知，增大孔隙率可以有效提升GDL的排水能力，工作电压大于0.6 V时，最大水摩尔分数随着孔隙率的增大而减小，即在小电流密度工况下，燃料电池反应生成水的量减少；孔隙率越大则平均水摩尔分数越小，说明增大孔隙率能有效优化扩散层内的水分布。

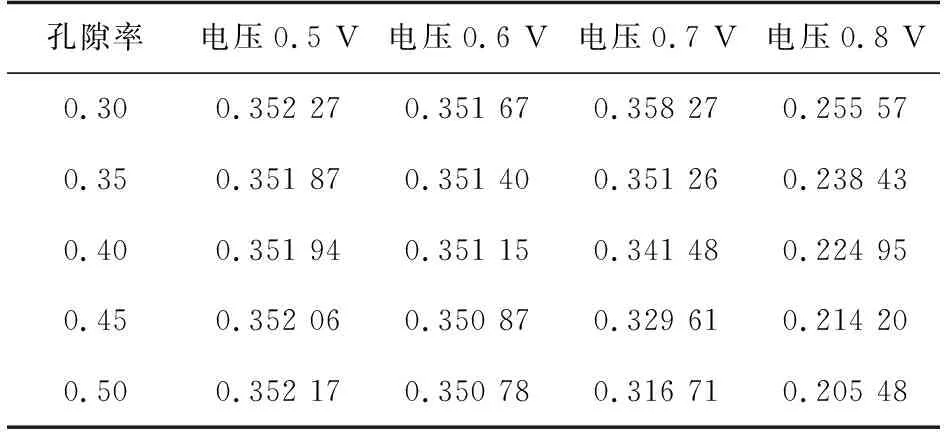
表2 不同电池电压和GDL孔隙率对应的最大水摩尔分数

表3 不同电池电压和GDL孔隙率对应的平均水摩尔分数

不同孔隙率下的电池极化曲线由图2所示。由图2可知，燃料电池的电流密度随着孔隙率的增大而增大，在大电流密度工况下尤为明显，说明增大孔隙率能有效提升燃料电池的输出功率。

图2 不同孔隙率下的电池极化曲线

根据上述可知，改变孔隙率是优化燃料电池输水性能和功率密度的重要方法。然而，孔隙率过大可能导致质子交换膜和催化层附近的水含量偏低，影响反应效率和电池寿命[13]。为了保证电池的良好排水性能且在质子交换膜附近保证一定的水摩尔分数，应进行孔隙率梯度设计。选取单一孔隙率为0.4的GDL作为基准GDL进行模拟，为保证孔隙率梯度分布是唯一影响GDL排水性能的因素，保持平均孔隙率为0.4，将GDL沿催化层到气体通道方向(称为厚度方向)进行分层，平均分为2层梯度或4层梯度结构，孔隙率沿厚度方向逐层递增，分别为：孔隙率为0.35/0.45的小梯度双层GDL、孔隙率为0.30/0.50的大梯度双层GDL和孔隙率为0.30/0.35/0.45/0.50的4层GDL，研究孔隙率梯度结构及其变化对缓解“水淹”能力的影响。

研究分析电压为0.50～0.85 V时不同方案GDL的水摩尔分数和水分布。此外，研究采用GDL孔隙率结构优化后PEMFC的极化曲线，分析孔隙率梯度分布对电池性能的影响。

采用梯度设计后，工作电压为0.8 V时，水摩尔分数分布如图3所示。由图3可知：在工作电压为0.8 V时，采用孔隙率梯度分布的GDL后，扩散层内的最大水摩尔分数明显下降；相比于单一孔隙率，采用小梯度双层GDL、大梯度双层GDL和4层GDL后，最大水摩尔分数分别下降了0.04、0.07、0.07。采用进行孔隙率梯度分布设计后的GDL能有效地缓解“水淹”问题。这一结论与文献[14]的试验结果一致，仿真结果可信。

图3 电压为0.8 V时不同方案电池的水摩尔分数分布

2 模拟结果分析

2.1 电流密度

不同孔隙率分层的极化曲线如图4所示。由图4可知：相比于基准GDL，采用不同孔隙率梯度设计后，均能不同程度地提高电池的输出性能；当PEMFC处于大电流密度工况时，在相同的工作电压下，双层梯度结构GDL和4层梯度结构GDL均能使电池有更良好的电流密度输出，而4层梯度GDL和大梯度双层GDL对电流密度的提升效果近似，且两者均比小梯度双层GDL有更加优异的输出性能；当工作电压大于0.7 V时，GDL梯度结构优化对电池的输出性能影响不大。

图4 不同孔隙率分层的极化曲线

孔隙率梯度设计优化了电池的排水能力，增大了氧气与催化层接触面积，提高了催化层内氧气的化学反应效率，电池性能得到提升；对于大电流密度工况，由于该工况更容易发生“水淹”，故双层梯度和4层梯度GDL能够更好地缓解“水淹”现象，对该工况下的电池性能有更好的提升效果。

2.2 基准GDL与小梯度双层GDL的水管理分析

采用双层孔隙率梯度设计后，不同电池电压下小梯度双层GDL与基准GDL的最大水摩尔分数和平均水摩尔分数如表4、5所示。

表4 基准和小梯度双层GDL的最大水摩尔分数

由表4知：孔隙率为0.40，电压由0.8 V下降到0.7 V时，PEMFC内部的含水量明显上升，最大水摩尔分数从0.224 95上升到0.341 48；当电压由0.7 V下降到0.5 V时，最大水摩尔分数几乎没有变化；平均孔隙率相同、电池电压为0.8 V时，与基准GDL相比，小梯度双层GDL的最大水摩尔分数下降到0.181 00；GDL在小电流密度工况下的排水性能得到改善；在大电流密度工况下，即当电池电压低于0.7 V时，该双层GDL的最大水摩尔分数与基准GDL相当。由此可得，小梯度双层GDL在小电流密度工况下具有比基准GDL更好的排水性能；而在电池处于大电流密度状态时，小梯底双层GDL对最大水摩尔分数影响不大。

由表5可知：采用双层GDL后，全工况下的平均水摩尔分数整体近似平行下降。这说明在大电流密度工况下，小梯度双层GDL能有效降低整体水含量，即优化了液态水在GDL内的分布。因此，采用具有孔隙率梯度的GDL对解决大电流密度工况下的“水淹”问题具有积极意义。

表5 基准和小梯度双层GDL的平均水摩尔分数

电池电压为0.6 V时，距离阴极流道入口15 mm处，双层梯度GDL与基准GDL的水分布云图如图5所示。

a) 基准GDL b) 小梯度双层GDL

由图5可知：基准GDL和小梯度双层GDL的最大水摩尔分数均为0.34，最小水摩尔分数均为0.02；但由于靠近流道处的扩散层孔隙率较大，小梯度双层GDL内的水含量相对更少，水位较低，且这一现象在靠近流道处的扩散层内更为明显。

2.3 4层梯度GDL的水管理分析

为进一步研究孔隙率梯度的变化对扩散层排水性能的影响，设计一种孔隙率沿厚度方向分布分别为0.30/0.35/0.45/0.50的4层GDL，并与基准GDL和小梯度双层GDL进行比较，结果如表6、7所示。电池电压为0.6 V时，4层梯度GDL水摩尔分数分布云图如图6所示。

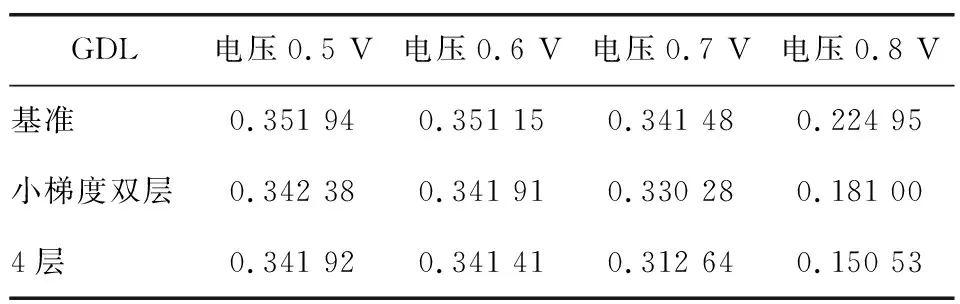
表6 基准、小梯度双层和4层GDL的最大水摩尔分数

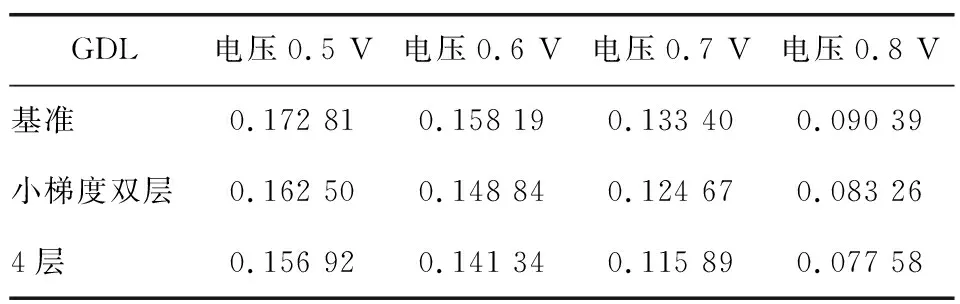
表7 基准、小梯度双层和4层GDL的平均水摩尔分数

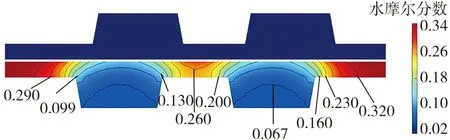
图6 4层梯度GDL水摩尔分数分布

由表6、7及图6可知：采用4层GDL后，PEMFC的排水能力比采用双层梯度GDL时更强；电压为0.7、0.8 V时，4层GDL的最大水摩尔分数相比于小梯度双层GDL分别下降了0.017 64、0.030 47；在大电流密度工况下，4层GDL的最大水摩尔分数为0.341 92，与小梯度双层GDL相当；全工况下，平均水摩尔分数曲线整体近似平行下移，GDL的整体排水能力进一步增强，大电流密度工况下的“水淹”现象得到更好的缓解，GDL内部的水分布进一步优化；相比于基准GDL和小梯度双层GDL，4层GDL内的水位更低，水含量更少，水管理能力进一步提升。

因此，增大孔隙率梯度结构的变化可以进一步优化GDL的排水能力，在大电流密度工况下尤为明显。

2.4 大梯度双层GDL的水管理分析

不同电池电压下，基准、小梯度双层、4层和大梯度双层GDL的最大水摩尔分数和平均水摩尔分数如表8、9所示。

表8 基准、小梯度双层、4层和大梯度双层GDL的最大水摩尔分数

表9 基准、小梯度双层、4层和大梯度双层GDL的平均水摩尔分数

由表8、9可知：大梯度双层GDL内的水摩尔分数与4层GDL时几乎一致，说明增大孔隙率梯度能够提升GDL的排水能力；增大孔隙率梯度后，工作电压为0.8 V时，相比基准GDL和小梯度双层GDL，大梯度双层GDL最大水摩尔分数分别下降了0.074 87和0.030 92，排水性能优化明显；另外，相比小梯度双层GDL，大梯度双层GDL在电池电压为0.7 V时拥有更优异的排水能力，最大水摩尔分数比基准GDL下降了0.029 43，而小梯度双层GDL仅下降了0.011 20；大梯度双层GDL的排水性能与4层GDL 的平均水摩尔分数几乎一致。

电压为0.6 V时，大梯度双层GDL在距离流道入口15 mm的水摩尔分数分布云图如图7所示。

图7 大梯度双层GDL水摩尔分数分布

由图7可知，电压为0.6 V时，大梯度双层GDL在距离流道入口15 mm的截面液面分布与4层GDL近似，均具有良好的排水能力。

因此， 增大孔隙率梯度变化的剧烈程度可以进一步强化GDL的排水性能，且与改变梯度变化效果相当，能更好地防止“水淹”发生。

3 结论

利用COMSOL Multiphysics软件构建PEMFC三维模型，设计了不同孔隙率梯度分布的GDL，分析了梯度分布结构在不同工况下对电池排水能力和电池性能的影响。在保持平均孔隙率不变的情况下，对单层、双层及4层GDL进行模拟分析。

1)孔隙率为0.30～0.50时，可以通过增大GDL的孔隙率来提升氢燃料电池的排水性能，缓解“水淹”问题，从而提升电池的输出性能，特别是在大电流密度工况下性能提升更明显。

2)采用平均孔隙率为0.40的GDL时，通过按梯度增加扩散层层数或梯度变化提高电池的水管理能力，有效提升电池性能；因此，通过对扩散层进行合理的孔隙率梯度设计可以提升燃料电池的水管理能力和输出性能，且水管理能力和输出性能提升的趋势相同。