基于喷射量波动的燃气发动机空燃比自适应控制器设计

孔雪艳，杨君，王明杰，王健，黄万友

1.山东交通学院 汽车工程学院，山东 济南 250357；2. 山东交通学院 机动车检测实验中心，山东 济南 250357

0 引言

天然气凭借安全可靠、经济实惠、污染小等优势成为车用清洁燃料的主力之一，为带动社会经济发展、促进环境改善提供了新的驱动力。与柴油机相比，同一功率下的天然气发动机燃烧成本更低，且天然气不含一氧化碳，燃烧后产生的二氧化碳、氮氧化物等排放较少。天然气发动机的排放受空燃比影响较大，因此对天然气发动机控制系统准确性要求日渐提升, 发动机故障诊断与自适应控制也受到了更为广泛的关注。

王春禄等[1]针对燃气发动机在控制模块、进气方式、混合方式等方面的差异，对不同形式燃气发动机的空燃比控制原理进行了较为详细的解读；Li等[2]研究了汽油直喷发动机空燃比调节问题，为减少空燃比调节时间，设计了一种比例积分(proportional integral, PI)模糊知识控制器，并通过试验验证了其有效性；杨君等[3]研究了燃气发动机废气再循环的随机调节问题，设计了一种随机调节器实现对缸内废气总质量的调节，并对调节器进行了仿真验证;崔宏宇等[4]分析了单燃料燃气发动机的空燃比控制问题，设计了PI控制器，通过调整燃气供给量控制空燃比,并对该控制系统进行数值仿真研究，结果表明该控制器具有较强的鲁棒性，可以将空燃比控制在理论值附近；Song等[5]建立汽油机空燃比模型，设计了一款空燃比控制器，通过调整模型参数减小误差和干扰，缩短空燃比的稳定时间，解决发动机空气流量估计不确定性和废气传输延迟问题，并通过汽油机试验台进行了试验验证；Yang等[6]研究了在沼气中甲烷浓度不确定情况下的空燃比控制问题，在自适应律的基础上设计了考虑残留气体随机性的随机自适应控制器，估计理论空燃比，并通过仿真研究验证了该控制器的有效性；张腾等[7]分析了天然气发动机过量空气系数、尾气中污染气体的浓度等因素对NH3排放的影响，比较分析了3种NH3排放控制方法，最后提出了采用三效催化转化器和NH3逃逸催化器方案对国六发动机的NH3排放进行控制处理;Arslan等[8]研究了内燃机在噪声和故障条件下的空燃比控制问题，提出了一种主动容错控制系统来控制空燃比，使系统在故障条件下仍能保持稳定，仿真结果表明，主动容错控制系统在故障条件下可以保持良好的空燃比，并且对噪声具有鲁棒性；Yang等[9]考虑到残余气体份数的随机循环变化，提出了一种空燃比随机最优控制方案，利用残余气体份数的空燃比动态模型设计出最优控制器，并通过仿真和试验验证了控制方案的有效性；Yang等[10]研究了压缩天然气发动机的空燃比调节问题，利用压缩天然气发动机的动态模型，设计了一款随机鲁棒空燃比调节器，抑制新鲜空气的不确定性波动，进而实现对空燃比的精确控制，并通过数值模拟验证调节器的性能；Shamekhi等[11]设计了一种具有自适应变函数的模型预测自校正调节器，用于燃油喷射反馈控制，以处理燃油喷射火花点火发动机控制瞬态过程中的壁面润湿效应，以优化发动机燃烧，提高发动机性能;Shahbaz等[12]研究了火花点火发动机的空燃比控制问题，提出一种基于人工神经网络的主动容错控制系统对空燃比控制系统传感器故障进行容错，并通过仿真试验验证了该系统的稳定性。

发动机燃气供给系统出现故障，会直接造成燃气喷射量偏离正常值，进而影响燃气发动机空燃比的控制精度和发动机的性能。本文中基于燃气发动机动力学模型，设计自适应空燃比控制策略，确定自适应律；通过李雅普诺夫方法验证控制器的稳定性；利用仿真平台验证3种工况下所设计控制器的有效性，有效控制燃气喷射量波动情况下的空燃比。

1 空燃比自适应控制器设计

自适应控制是一种为应对未知参数和干扰而兴起的技术，目前已经发展得相当成熟。它能够根据外界环境或系统参数的变化自动调节系统或控制参数，进而满足系统的性能指标。

天然气发动机气路、油路动态方程[9]为：

Ma(k+1)=r(k)[Ma(k)-λdMf(k)ηc(k)]+Man(k)，

(1)

Mf(k+1)=r(k)[1-ηc(k)]Mf(k)+Mfn(k)，

(2)

式中：Ma(k)为气缸内总空气质量，kg；r(k)为残存气体份数；k为计算循环数；λd为理想空燃比，λd=17.4；Mf(k)为气缸内燃气总质量，kg；ηc(k)为燃烧效率，ηc(k)∈[0,1]；Man(k)为吸入缸内的新鲜空气质量，kg；Mfn(k)为进入缸内的燃气质量，kg。

引入燃气供给系统失效因子ρ衡量天然气发动机燃气供给系统管路堵塞、压力波动等对燃气喷射量造成的影响。对于所有可能发生的故障模式，0<ρ≤1，ρ=1时表示系统工作状况正常，0<ρ<1时表示系统出现部分故障。引入ρ后，天然气发动机油路的动力学方程可表示为：

Mf(k+1)=r(k)[1-ηc(k)]Mf(k)+ρMfn(k)。

(3)

天然气发动机空燃比调节误差

y(k)=Ma(k)-Mf(k)λd。

(4)

由式(1)(3)(4)可以得出如下系统：

(5)

对式(5)进行整理可得：

y(k+1)=Ma(k+1)-Mf(k+1)λd=r(k)y(k)+Man(k)-ρλdMfn(k)。

(6)

(7)

式中c、Γ均为设计参数。

对于任意的ρ∈(0,1)，都有：

(8)

在一定的故障模式下，根据渐进稳定判据要求，可得：

(9)

利用自适应律计算k+1循环的未知量

(10)

整理式(10)可得：

(11)

由式(11)可推导出：

(12)

(13)

将式(13)代入式(11)，整理得到：

(14)

将式(14)代入不等式(9)，得到：

(15)

根据渐近稳定性判据要求，抵消平方项，则设计喷入气缸的燃气质量Mfn(k)为：

(16)

式中ε为设计参数。将式(16)代入式(15)，得到：

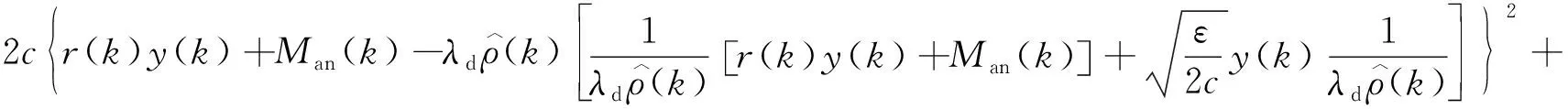
(17)

根据李雅普诺夫稳定判据，为使控制器能较好地将天然气发动机的空燃比控制在理想值附近，应使式(17)满足：

(18)

为抵消式(17)中最后平方项，应满足以下条件：

(19)

由式(19)可知γ需满足：

(20)

由式(18)(20)可知，控制器设计参数应该满足以下条件：

(21)

式中：min{Mfn(k)}为某个循环下进入缸内的最小燃气质量，kg。

由式(17)(18)可知，满足以上条件时，闭环系统是李雅普诺夫稳定的，所设计的自适应控制器能够使空燃比回归到理想值附近。另外，通过选取适当的参数γ和c，能够使空燃比的调节误差控制在较小邻域内。

2 仿真验证

利用Matlab/Simulink仿真平台，对所设计的控制器进行验证。根据式(5)和相关天然气发动机仿真模型[9]，搭建的仿真模型如图1。

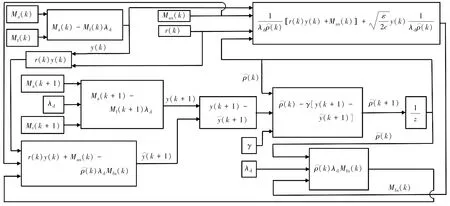
图1 空燃比控制仿真模型

分别选取3种工况对所设计的控制器的有效性进行验证：1)工况W1，发动机转速为1200 r/min，外部负载为60 N·m；2)工况W2，发动机转速为1600 r/min，外部负载为30 N·m；3)工况W3，发动机转速为1600 r/min，外部负载为60 N·m。

当ρ=0.5、0.7时，3种不同工况下的空燃比信号如图2～4所示。

a) ρ=0.5 b) ρ=0.7

a) ρ=0.5 b) ρ=0.7

a) ρ=0.5 b) ρ=0.7

考虑到在天然气发动机运行过程中可能出现的不确定因素，将ρ定义为由1—0.8—0.85的跳变信号，通过仿真得到W2工况下的空燃比信号如图5所示。

图5 工况W2、ρ跳变信号的空燃比信号

由图2～5可知：1)当ρ=0.5时，空燃比信号的波动幅度较小；ρ为0.7时，空燃比信号波动稍大；2)在ρ为常数的情况下，所设计的自适应控制器在3种不同工况下均能将天然气发动机的空燃比控制在理想值附近，具有良好的控制效果；3)当ρ为跳变信号时，控制器仍能将空燃比调节到理想值范围附近，以W2工况为例，自适应控制器也能将天然气发动机空燃比控制到理想值的较小邻域内，控制效果良好。

3 结语

针对天然气发动机燃气供给系统故障引起的燃气喷射量波动问题，设计空燃比自适应控制器，通过调整燃气喷射量将天然气发动机的空燃比控制在理想值附近。利用Matlab/Simulink仿真平台，搭建天然气发动机空燃比控制模型，验证3种运行工况下该自适应控制器的有效性，当燃气供给系统发生故障造成燃气喷射量偏离正常值时，该控制器可以有效抑制燃气喷射量不确定对空燃比控制精度的影响。