管内小药量水下爆炸平面冲击波形成方法及其应用

徐维铮, 黄 宇, 李业勋, 赵宏涛, 郑贤旭

管内小药量水下爆炸平面冲击波形成方法及其应用

徐维铮, 黄 宇, 李业勋, 赵宏涛, 郑贤旭

(中国工程物理研究院 流体物理研究所, 四川 绵阳, 621999)

水下爆炸过程中存在冲击波、气泡、冲击波绕射等多种效应的耦合, 给水下爆炸毁伤机理的研究带来了一定难度。为了对上述多种效应进行解耦, 文中提出一种管内小药量水下爆炸平面冲击波形成方法, 采用数值仿真和理论分析对管内水下爆炸平面冲击波的衰减规律进行了研究。研究结果表明: 在管道端部放置装药配合端面起爆, 可在管内形成指数衰减形式的平面冲击波; 理论模型与数值计算结果吻合较好, 可给出冲击波超压峰值随距离的衰减关系, 以及不同时刻冲击波的阵面位置。最后给出了该试验方法在水下爆炸加载典型结构件毁伤效应和流固耦合作用机理研究的应用场景。研究成果可为水下爆炸毁伤评估提供参考。

水下爆炸; 平面冲击波; 冲击加载; 流固耦合

0 引言

随着现代精确制导武器和高速水中兵器的快速发展, 舰艇在服役过程中受到水下爆炸冲击的威胁越来越多, 如何提高舰艇结构的抗爆、抗冲击能力成为了衡量舰艇生命力的重要指标之一。

传统的舰艇结构水下爆炸抗冲击测试主要在爆炸水池或爆炸水箱中开展。然而此类测试不仅涉及繁杂的试验协调准备, 同时试验可控性和重复性较差; 除了冲击波载荷外, 无法有效避免气泡脉动载荷以及自由面、绕射稀疏效应对冲击波加载过程的影响。针对传统研究方法中所存在的问题, 研究者们发展了在管内产生水下爆炸冲击波的试验仿真方法[1]。

其中一种方法是通过克级装药在锥形激波管内形成水下爆炸冲击波。Filler[2]首先提出了锥形激波管水下爆炸试验装置的原理。Coombs 等[3]对锥形管内原始冲击波和膨胀波的绕射叠加过程进行了计算, 认为采用该原理可以实现小药量下的大冲击波幅值加载。Zalesak 等[4]在该原理基础上, 设计了锥形激波管, 用于美国海军研究实验室开展的相关试验。试验时, 在锥形管内装满水, 尖头一端填装少量炸药, 宽头一端放置试件, 见图1。

图1 锥形激波管原理和实物图Fig. 1 Principle of conical shock tube and on-site picture

Heshmati 等[5-6]采用数值仿真方法探讨了锥形激波管的长度、锥角和药量等因素对冲击波载荷的影响规律, 并采用长3.105 m, 锥角为3.2°的锥形冲击管, 对不同厚度、不同材料的金属板进行了水下爆炸加载响应试验。Leblanc 等[7-9]采用长度为5.25 m, 锥角为2.6°的锥形激波管装置对含聚脲涂层和玻璃内芯的复合材料层合板的抗爆性能进行了研究, 详细分析了管内发生的流固相互作用过程。

另一种方法是通过轻气炮发射高速飞片撞击活塞的非装药加载方式在管内形成水下爆炸冲击波。Deshpande 等[10]提出了一种非装药的水下爆炸冲击波仿真试验装置, 并对形成的冲击波载荷传播规律和参数进行理论分析。Espinosa 等[11]考虑缩比条件和轻气炮口径条件的约束, 设计了一种“扩散型”的非装药水下冲击加载装置, 该装置主体为圆锥形水仓, 通过轻气炮系统发射飞片撞击圆锥形水仓获得冲击载荷, 如图2 所示。项大林[12]、任鹏[13]、杨一方等[14]也对此类装置开展了设计和研究, 并基于该装置开展了典型复合材料构件的冲击加载特性研究[15-17]。

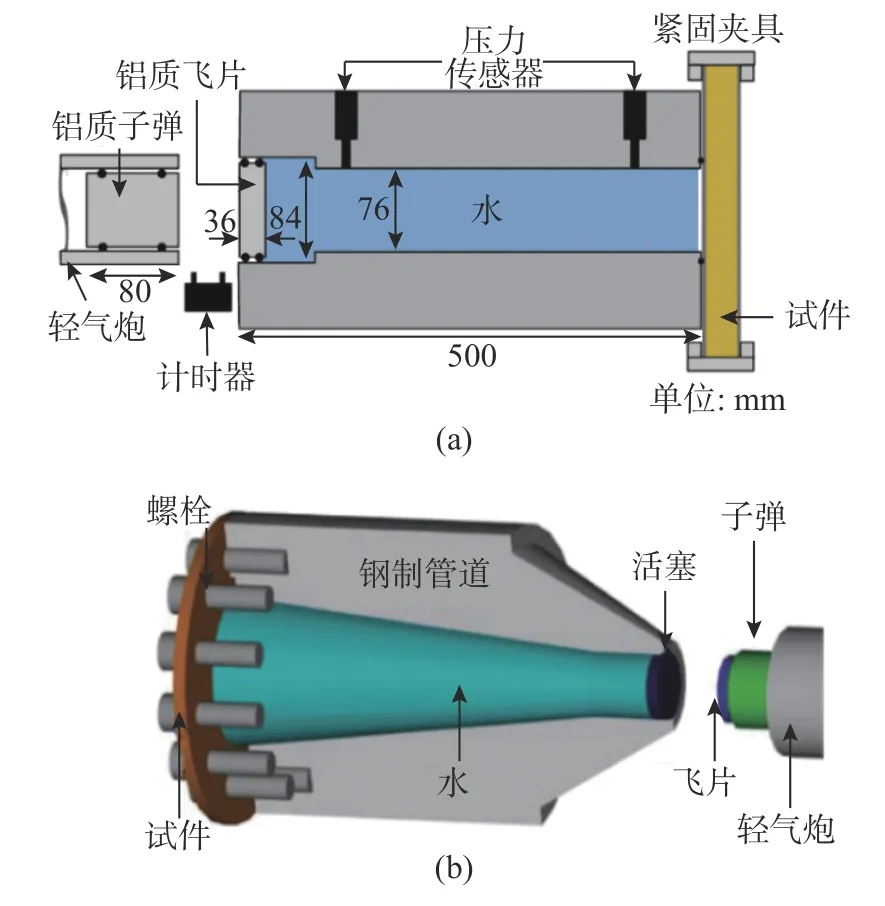
图2 非药式水下爆炸冲击加载装置示意图Fig. 2 Schematic diagram of non-explosive underwater shock loading device

对上述研究现状进行分析可知, 锥形激波管是一种基于装药的水下爆炸冲击波形成方式, 其优点是采用较小的药量能较好地仿真水下冲击波载荷, 然而其存在如下缺点: 1) 装药在锥形管内爆炸,导致其结构壁较厚, 结构加工复杂, 整体装置笨重等; 2) 冲击波在试件和管壁之间的多次反射会导致对试件的额外加载。

非装药水下爆炸冲击波仿真装置可在实验室内反复使用, 为水下冲击载荷作用下金属/复合结构的响应特性研究提供了很好的试验手段, 然而其存在如下缺点: 1) 装置复杂、成本较高, 试验需要较为复杂的操作流程; 2) 形成的冲击波波形局部震荡问题较严重, 波形不够平滑; 3) 冲击波在试件和活塞之间的多次反射也会导致对试件的额外加载。

为此, 文中提出一种管内小药量水下爆炸平面冲击波形成方法, 采用等直径圆管模拟水仓, 避免冲击波在传播路径中的变截面问题; 装药在圆管端部采用单点/多点起爆方式以在水中形成平面冲击波。该试验方法可用于开展水下爆炸冲击波加载下典型结构件毁伤效应和流固耦合作用机理研究, 为水下爆炸毁伤评估研究提供参考。

1 数值仿真

1.1 数值计算模型

由于圆管的对称性, 数值仿真采用二维轴对称模型, 圆管长度为600 mm, 管径为60 mm; 为在管内形成平面冲击波, TNT 装药直径与管径相同取值为60 mm, 装药高度H0分别为5、10、20 mm, 装药左端面采用平面起爆的方式。在数值计算中,装药位置分为2 种: 1) 装药放置在管内且管左端面为约束状态, 见图3(a); 2) 装药放置在管外, 装药右端面紧贴管道左端面, 见图3(b)。

图3 计算域图Fig. 3 Computational domain

水下爆炸冲击波传播速度较快, 当管壁约束足够强时, 可不考虑管壁对冲击波传播的影响, 因此在数值计算中将管壁设置为刚性壁面, 空气域边界设置为无反射边界, 网格尺寸统一设置为0.5 mm。

采用Autodyn 中二维轴对称多物质欧拉求解器进行求解, 其中水的状态采用多项式状态方程描述, 其在压缩状态µgt;0 和拉伸状态µlt;0 的表达式分别为

式中:µ=ρ/ρ0−1,ρ为水压缩后的密度;ρ0为水的初始密度;A1、A2、A3、B0、B1、T1、T2为材料参数, 取值见表1。

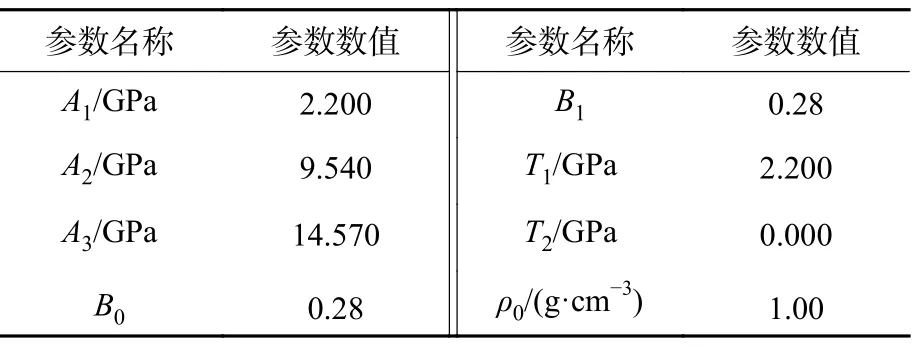
表1 水的材料参数Table 1 Material parameters of water

TNT 炸药爆轰产物的状态采用Jones-Wilkins-Lee 状态(方程描述), 其表达(式为)

式中:V为相对比容;A、B、R1、R2、w为炸药材料参数, 具体数值见表2。表中ρe为炸药密度;pCJ为爆轰压力;DCJ为爆轰速度。

表2 TNT 炸药的材料参数Table 2 Material parameters of TNT

空气的状态采用理想气体状态方程描述, 其表达式为

式中,γa=1.4 为空气的绝热指数。

1.2 数值仿真结果与分析

图4、图5 分别给出装药高度H0=5 mm, 放置于管内/管外爆炸工况下, 不同时刻管道内冲击波传播过程压力云图。

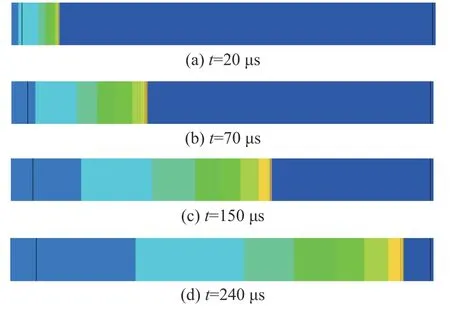
图4 典型时刻压力计算云图(H0=5 mm, 装药在管内)Fig. 4 Computational contour of pressure at typical times with explosives inside the tube(H0=5 mm)

图5 典型时刻压力计算云图(H0=5 mm 装药在管外)Fig. 5 Computational contour of pressure at typical times with explosives outside the tube(H0=5 mm)

分析图4、图5 可知, 2 种装药放置方式均能在管内形成较好的平面冲击波。当装药放置在管外时, 部分装药能量用于在空气中形成冲击波, 导致只有部分能量用于在水中形成冲击波, 使得冲击波传播速度随传播距离衰减较快。

图6、图7 分别给出装药高度H0=5 mm, 放置于管内/管外爆炸工况下, 典型测点处超压时间历程曲线。

分析图6、图7 可知, 2 种装药放置方式均能在管内形成指数衰减形式的冲击波, 可较好仿真真实水下爆炸冲击波波形。当装药放置在管外时,由于能量损失, 冲击波超压峰值随传播距离衰减较快, 定点位置处的超压随时间衰减速率也较快。

2 冲击波衰减规律分析

在文献[18]研究的基础上, 基于一维冲击波理论、水的非线性D-u关系和能量法对其建立近似分析模型, 可求解得到管内不同时刻冲击波阵面的位置和超压峰值随传播距离的衰减计算公式。

图6 典型测点位置超压时间历程曲线(H0=5 mm, 装药在管内)Fig. 6 Time-history curves of overpressure at typical locations with explosives inside the tube(H0=5 mm)

图7 典型测点位置超压时间历程曲线(H0=5 mm 装药在管外)Fig. 7 Time-history curves of overpressure at typical locations with explosives outside the tube(H0=5 mm)

2.1 分析模型

冲击波阵面质量、动量和能量关系采用如下方程进行描述

式中:D为冲击波速度;u为冲击波后粒子速度;p为冲击波阵面压力;E为单位质量水的总能量(内能和动能)。

水的非线性D-u关系为

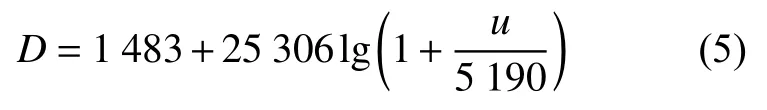
根据式(4)可将总能跳跃关系表达为波后粒子速度的关系, 即

按文献[18]中思路, 令总能跳跃关系式为

式中:H为冲击波传播距离;S为管道截面积;Q为炸药爆炸释放的总能量;α为无量纲比例常数。α的求解可根据爆炸初始界面时刻取极限得到, 即

在爆炸初始时刻, 水和爆轰产物界面两侧满足压力和流体速度的连续条件, 初始界面处水介质的质点速度u*和压力p*分别为[19]

式中,γ为炸药爆轰产物绝热指数。联立式(9)和式(5), 采用牛顿迭代法可求解得到爆炸初始时刻水中冲击波的状态参数, 进而得到式(8)中无量纲比例常数α的数值。

根据式(6)和式(7)建立冲击波波后粒子速度与冲击波传播距离之间的关系

将式(5)代入式(4)中第1 式可得

进一步将式(11)代入式(10)可得冲击波波后粒子速度与传播距离的关系

根据式(12)可知, 可通过牛顿迭代法获得冲击波各物理量与传播距离的衰减变化关系, 同时根据冲击波传播速度和距离的关系

可得不同时刻冲击波阵面的位置。

2.2 分析模型与数值对比

图8、图9 分别给出3 种装药高度, 放置于管内/管外爆炸工况下, 不同无量纲比值H/H0处超压峰值数值与理论对比结果, 通过理论与数值的对比发现, 当装药在管外时β=1/3, 即仅有1/3 装药的能量用于在水中形成冲击波。

图8 不同无量纲比值H/H0 超压峰值数值与理论对比曲线(装药在管内)Fig. 8 Curves of numerical and theoretical overpressure at different values of H/H0 with explosives inside the tube

图9 不同无量纲比值H/H0 超压峰值数值与理论对比曲线(装药在管外)Fig. 9 Curves of numerical and theoretical overpressure at different values of H/H0 with explosives outside the tube

图10、图11 分别给出3 种装药高度, 放置于管内/管外爆炸工况下, 冲击波阵面位置随时间变化关系数值与理论对比结果, 两者吻合较好, 说明文中给出的管内冲击波计算模型具有一定的可靠性, 可在后期用于快速给出管道内冲击波传播规律, 同时也可为管道结构设计提供参考。

图10 冲击波阵面位置随时间变化关系数值与理论对比曲线(装药在管内)Fig. 10 Curves of numerical and theoretical locations of shock waves at different time with explosives inside the tube

图11 冲击波阵面位置随时间变化关系数值与理论对比曲线(装药在管外)Fig. 11 Curves between numerical and theoretical locations of shock waves at different time with explosives outside the tube

3 应用实例

下文首先探讨了真实试验中起爆方式的选择,接着给出了该试验方法的3 个应用实例。

3.1 起爆方式选择

平面波发生器是驱动装药形成平面波的有效手段, 采用端面起爆方式(即类似平面波发生器)对管道内冲击波传播进行数值仿真。然而在实际的加载试验中, 希望采取尽可能简单的方式获得所需要的压力波形, 由于重点关注区域为管道后段(爆炸远场区域) 的压力分布, 为此, 应采取不同的起爆方式观察管道内压力波传播的历程。

图12 给出了单点中心起爆冲击波传播云图及典型测点压力。分析可知, 单点起爆后, 在爆炸初期冲击波阵面呈现近似弧面, 后续传播过程中由于管壁的约束, 逐渐演化为近似平面波进行传播。图13 给出了多点起爆冲击波传播云图及典型测点压力, 分析可知, 多点起爆后, 有效改善了爆炸初期冲击波阵面的弯曲, 后续传播过程中由于管壁的约束, 逐渐演化为近似平面波进行传播。即采用单点中心起爆或者多点起爆的方式均能有效获得所需要的波形。

图12 单点中心起爆冲击波传播云图Fig. 12 Computational contours of shock waves at different times using single point initiation

3.2 爆炸冲击波载荷作用下典型复合材料构件响应与破坏分析

采用高强度钢作为管道的材料, 管道内设置若干典型压力测点, 测量冲击波压力时间历程曲线;采用激光干涉测速系统获得冲击波加载下典型复合材料构件的冲击波响应速度历程曲线, 最后采用三维激光扫描成像设备获得响应与破坏的数字图像, 试验示意图见图14。

图13 多点起爆冲击波传播云图Fig. 13 Computational contours of shock waves at different times using multi-point initiation

图14 典型复合材料构件加载示意图Fig. 14 Schematic diagram of loading typical composite components

3.3 水下爆炸冲击波与典型结构件耦合作用分析

水下爆炸冲击波与典型结构件的耦合作用过程中不仅存在波系反射结构, 同时会在构件与水交界面处形成局部空化效应。为观察到流固耦合作用过程中的物理现象, 在管道后端设置观察段,管壁材料采用K9 玻璃等高强度透光材料, 结合LED 长照明光源和高速相机可捕捉获得上述物理现象, 配合压力测试和激光干涉测速可为流固耦合作用机理研究提供较好的试验数据, 试验示意图见图15。

图15 冲击波与典型结构件耦合作用机理试验示意图Fig. 15 Schematic diagram of shock waves coupling with typical structures

3.4 水下爆炸冲击波与结构物相互作用分析

水下爆炸过程中不可避免涉及冲击波与船体结构、港口附近水中结构物的相互作用(涉及冲击波入射、反射和绕射等复杂波系), 会造成船体结构和水中结构物发生一定的刚体运动。采用上述试验方法可开展水下爆炸冲击波与结构物的相互作用研究, 结合高速相机获得绕射波系结构和结构运动与冲击波强度的关系, 试验示意图见图16。

图16 冲击波与结构物相互作用示意图Fig. 16 Schematic diagram of shock waves interacting with structures

4 结束语

文中提出一种管内小药量水下爆炸平面冲击波形成方法, 采用数值仿真和理论分析相结合方式对管内水下爆炸冲击波衰减规律进行了研究,并给出该试验方法的推广应用实例。研究表明:

1) 装药放置在管端部配合端面起爆可在管内形成指数衰减形式的平面冲击波, 当装药放置在管外时, 仅有约1/3 能量用于在水中形成冲击波,导致冲击波超压衰减速率加快;

2) 理论模型与数值计算结果吻合较好, 可给出冲击波超压峰值随距离的衰减关系和不同时刻冲击波阵面位置;

3) 该试验方法可用于开展水下爆炸加载典型结构件毁伤效应和流固耦合作用机理等研究, 可为水下爆炸毁伤评估提供一定的参考。

[1]郑 监, 卢芳云, 李翔宇. 金属板在水下爆炸加载下的动态响应研究进展[J]. 中国测试, 2018, 44(10): 20-30.

Zheng Jian, Lu Fang-yun, Li Xiang-yu. Research Progress on Dynamic Response of Metal Plate in Underwater Explosion Loading[J]. China Measurement amp; Test, 2018, 44(10):20-30.

[2]F iller W S. Propagation of Shock Waves in a Hydrodynamic Conical Shock Tube[J]. Physics of Fluids, 1964, 7(5): 664-667.

[3]C oombs A, Thornhill C K. An Underwater Explosive Shock Gun[J]. Journal of Fluid Mechanics, 1967, 29(2): 373-383.

[4]Z alesak J F, Poche L B. The Shock Test Facility: An Explosive-driven, Water-filled Conical Shock Tube[C]//60th Shock and Vibration Symposium. The United States: The Acoustical Society of America, 1989.

[5]H eshmati M, Zamani J, Mozafari A. The Experimental and Numerical Impacts of Geometrical Parameters of Conical Shock Tube on the Function, Maximum Pressure and Generative Impulses to Expose Equivalent Mass and Behavioral Equation[J]. Materialwissenschaft Und Werkstofftechnik,2016, 47(7): 623-634.

[6]H eshmati M, Zamani A J, Mozafari A. Experimental and Numerical Study of Isotropic Circular Plates ’ Response to Underwater Explosive Loading, Created by Conic Shock Tube[J]. Materialwissenschaft Und Werkstofftechnik, 2017,48(2): 106-121.

[7]L eblanc J, Shukla A. Dynamic Response of Curved Composite Panels to Underwater Explosive Loading: Experimental and Computational Comparisons[J]. Composite Structures,2011, 93(11): 3072-3081.

[8]L eblanc J, Shukla A. Response of E-glass/vinyl Ester Composite Panels to Underwater Explosive Loading: Effects of Laminate Modifications[J]. International Journal of Impact Engineering, 2011, 38(10): 796-803.

[9]L eblanc J, Gardner N, Shukla A. Effect of Polyurea Coatings on the Response of Curved E-Glass/Vinyl Ester Composite Panels to Underwater Explosive Loading[J]. Composites Part B Engineering, 2013, 44(1): 565-574.

[10]D eshpande V S, Heaver A, Fleck N A. An Underwater Shock Simulator[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2006, 462(2067):1021-1041.

[11]E spinosa H D, Lee S, Moldovan N. A Novel Fluid Structure Interaction Experiment to Investigate Deformation of Structural Elements Subjected to Impulsive Loading[J]. Experimental Mechanics, 2006, 46(6): 805-824.

[12]项 大林, 荣吉利, 何轩, 等. 等效水下爆炸冲击加载装置的设计研究[J]. 兵工学报, 2014, 35(6): 857-863.

Xiang Da-lin, Rong Ji-li, He Xuan, et al. Development of an Equivalent Equipment on Underwater Explosion Impulsive Loading[J]. Acta Armamentarii, 2014, 35(6): 857-863.

[13]任 鹏, 张伟, 黄威, 等. 非药式水下爆炸冲击波加载装置研究[J]. 爆炸与冲击, 2014, 34(3): 334-339.

Ren Peng, Zhang Wei, Huang Wei, et al. Research on Nonexplosive Underwater Shock Loading Device[J]. Explosion and Shock Waves, 2014, 34(3): 334-339.

[14]杨 一方, 郭锐, 刘萌萌, 等. 一种新型水下爆炸冲击等效加载实验方法[J]. 鱼雷技术, 2014, 22(5): 357-360.

Yang Yi-fang, Guo Rui, Liu Meng-meng, et al. An Equivalent Loading Method for Underwater Explosion Impact Experiment[J]. Torpedo Technology, 2014, 22(5): 357-360.

[15]项 大林, 荣吉利, 何轩, 等. 基于三维数字图像相关方法的水下冲击载荷作用下铝板动力学响应研究[J]. 兵工学报,2014, 35(8): 1210-1217.

Xiang Da-lin, Rong Ji-li, He Xuan, et al. Dynamics Analysis of AL Plate Subjected to Underwater Impulsive Loads Based on 3D DIC[J]. Acta Armamentarii, 2014, 35(8): 1210-1217.

[16]任 鹏, 田阿利, 张伟, 等. 水下冲击波载荷作用下气背固支圆板动态毁伤实验[J]. 爆炸与冲击, 2016, 36(5): 617-624.

Ren Peng, Tian A-li, Zhang Wei, et al. Failure Mode of Clamped Air-back Circular Panel Subjected to Underwater Shock Loading[J]. Explosion and Shock Waves, 2016, 36(5):617-624.

[17]任 鹏, 张伟, 刘建华, 等. 水下冲击波作用的铝合金蜂窝夹层板动力学响应研究[J]. 振动与冲击, 2016, 35(2): 7-11.

Ren Peng, Zhang Wei, Liu Jian-hua, et al. Dynamic Analysis of Aluminium Alloy Honeycomb Core Sandwich Panels Subjected to Underwater Shock Loading[J]. Journal of Vibration and Shock, 2016, 35(2): 7-11.

[18]S ingh V P, Madan A K, Suneja H R, et al. Propagation of Spherical Shock Waves in Water[J]. Sadhana, 1980, 3(2):169-175.

[19]安 丰江, 吴成, 王宁飞. 水下爆炸能量耗散特性分析研究[J].北京理工大学学报, 2011, 31(4): 379-382.

An Feng-jiang, Wu Cheng, Wang Ning-fei. A Research on the Energy Dissipation of Underwater Explosion[J]. Transactions of Beijing Institute of Technology, 2011, 31(4): 379-382.

Formation Method of Planar Shock Waves in Underwater Explosions Using Small Charges inside a Tube and Its Applications

XU Wei-zheng,HUANG Yu,LI Ye-xun,ZHAO Hong-tao,ZHENG Xian-xu

(Institute of Fluid Physics, China Academy of Engineering Physics, Mianyang 621999, China)

Shock waves, bubbles, and diffraction effects during underwater explosions, as well as the coupling of these effects, make the investigation of underwater explosion damage complicated. In this paper, an experimental method for forming planar shock waves underwater using small charges inside a tube is presented to decouple these effects. Numerical simulations and theoretical models are used to explore the attenuation rules of planar shock waves in a tube. It is determined that planar shock waves with exponential attenuation forms can be generated by placing the charge at one end of the tube to achieve end-plane detonation. Theoretical results combined with overpressure peak versus distance curves and shock wave location versus time curves coincide well with simulation results. Applications of the proposed experimental method include the analysis of damage effects on typical structures and exploration of fluid-solid coupling mechanisms. The presented results also provide guidance for the damage evaluation of underwater explosions.

underwater explosion; planer shock wave; impact loading; fluid-solid coupling

TJ55; U662.3

A

2096-3920(2022)03-0405-08

10.11993/j.issn.1673-1948.2022.03.018

徐维铮, 黄宇, 李业勋, 等. 管内小药量水下爆炸平面冲击波形成方法及其应用[J]. 水下无人系统学报, 2022,30(3): 405-412.

2022-02-28;

2022-03-18.

中国工程物理研究院培育基金(PY20200003); 装备预先研究领域基金(80928010101) .

徐维铮(1991-), 男, 博士, 主要研究方向为水下爆炸毁伤.

(责任编辑: 吴 攀)