初中几何入门教学的对策与感悟

2022-07-12张雪春吴先才

名师在线 2022年21期

文 /张雪春吴先才

引言

我们经常在课后听到学生说：“老师，我在您的几何课堂上都会听得懂，但在课后做作业时，就是不知道如何去表达、怎样去书写。”笔者认为最大的原因在于：在几何入门阶段，学生没有掌握好基础知识，尤其是在“图”的问题上没有掌握好，从而影响了几何中“三种语言”的掌握与互换，造成一系列的恶性循环。因此，笔者认为，初中生刚刚接触几何学习时，上好几何入门课，尤其是上好“读图、识图、画图、作图”课至关重要。

下面，笔者从四个方面谈谈几何入门教学的几点对策与个人感悟。

一、立足学科基础，培养学习兴趣

我国古代著名的教育家孔子，在《论语》中曾提到“知之者不如好之者,好之者不如乐之者”，也就是说，兴趣是最好的老师。因此，在初中平面几何入门阶段，教师应致力于培养学生对学习平面几何的兴趣。

（一）赏几何的图形之美，培养学习几何的兴趣

在我们的现实生活中，建筑设计、生活用品、交通工具等，处处展现着“几何的图形之美”，时时彰显着“几何的无穷魅力”，只要我们拥有一双睿智的眼睛，就能进入几何的“世外桃源”中寻找其中的奥秘[1]。

在初中平面几何的第一节课，教师可提前准备一些适合这个年龄段，且学生比较感兴趣的、比较贴近他们日常生活的素材，让他们进行赏析与辨析，感受几何图形的魅力与神奇。如教师可给学生展示他们非常熟悉的苹果手机的标识图案，并提出问题：“很少有人会思考，这个图案是怎么画出来的。我们利用数学的作图工具是否能够完成？”教师可以此激发学生的好奇心，培养他们的学习兴趣。

同时，教师还可以通过现代教学辅助工具——几何画板或电子白板等，给学生展示各种动感、奇特、美妙的几何图形，如京剧脸谱的折叠、计算机体层成像（CT）、正方体的截面、心脏曲线、鹦鹉螺的对数螺纹线等。这样，学生才会怀着好奇心去体验几何图形的神奇之美，从而激发求知欲，更加喜欢学习几何知识。

（二）悟几何应用价值，点燃学习热情

教师可将几何知识与生产建设、日常生活中的相关应用密切联系起来，激发学生对几何的学习热情。例如，“将一条弯曲的河道改直，可以大大地缩短航程，你能说说其中蕴含的数学道理吗？”让学生理解与掌握“两点之间，直线最短”；又如：“木匠师傅在锯木料时，会先在木料上画出A、B两个点，然后过A、B两点弹出一条笔直的墨线，你能说说他这样做的道理吗？”让学生理解与掌握“两点可以确定一条直线”的公理。

如图1，在学校举办的田径运动会中，作为裁判员，你需要测量小明同学的跳远比赛成绩，怎样去测量才能比较准确地得到小明的跳远比赛成绩呢？学生通过亲身体验，亲自参与，可以从中悟出“垂线段最短”的道理；又如，古代有一位将军从A地出发，想把战马牵到河边的某处饮水，然后再到军营B地进行视察，他怎样走才能使路程最短呢？教师可以借助多媒体的动画演示，让学生通过猜想、尝试、画图、验证等操作，慢慢地理解和掌握“将军饮马”的数学建模思想，为以后的综合应用奠定基础。

图1

由此，通过这种生活情景数学化的几何教学，学生可以亲身体验到数学来源于生活，又服务于生活，更愿意在生活中探究和应用数学知识，体会数学与自然及人类社会的密切关系，更好地理解数学的价值，提高数学综合素养，感受到解决数学问题的快乐。

二、利用基本图形，训练作图技能

在直线、射线、线段的概念及其画法的教学过程中，教师通过下面题组的训练，一方面可以锻炼学生对最基本作图工具（直尺、圆规）的熟练使用，另一方面可以训练学生的画图、作图的能力与技巧，同时，还可以培养学生对数学语言中的文字语言、图形语言两种语

言之间的互转、互译能力[2]。

如图2，在一个平面内有A、B、C、D四点，请你根据下列所给的语句画出图形。

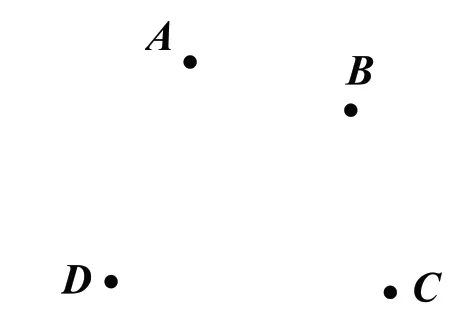
图2

(1)画线段BD。

(2)画射线AC。

(3)画直线CD。

(4)连接AD，并将其延长到E，使得DE=2AD。

待学生训练后，教师可将问题（4）进行如下变式：连接AD，并将其反向延长到E，使DE=2AD。通过这样的变式训练，学生能深刻理解“延长”与“反向延长”之间的联系与区别，并辨别上述两处“DE=2AD”的差异；同时，还可培养审题能力、析题能力和表达能力。

在进行“作一条线段等于已知线段”教学时，由于学生第一次接触尺规作图，因此，教师必须详细分析、耐心引导、亲自操作、规范演示等“画图”过程，然后再教学生如何“画图”。在此基础上，学生就提升了“线段的和与差”及“线段和差倍的综合”的“画图”能力。

在教学过程中，教师应加强对基本图形的作图训练，让学生动手、体验、模仿，并能熟练操作，这有利于培养学生的直观想象、动手操作和逻辑推理能力。

三、规范图形表达，提高转化能力

语言是一切教学活动得以顺利开展的必备工具。但对于初中平面几何中的数学语言来说，其主要包括文字语言、符号语言和图形语言。要学好几何，学生就必须学会利用数学语言准确、规范地表达、阐述相关的数学问题。因此，正确掌握这三种语言的互换与互译，是学好平面几何的前提和基础[3]。

在课堂教学过程中，教师可以组织学生开展开放式的探究性学习活动。如观察图3，你可以得出哪些结论？经过学生的小组合作交流与充分讨论，教师可以引导学生从以下几个方面得出结论。

图3

（1）点与直线的关系：点A、B、C在同一条直线上（或A、B、C三点共线）；点A在直线BC上；直线AB过点C。

（2）直线：直线AB，或直线AC，或直线BC。

（3）线段：线段AC、线段AB、线段CB。

（4）射线：射线AC、射线AB、射线CB。

（5）角：∠ACB=180°。

这样的题组训练一方面可以增强学生的语言表达能力，特别是澄清了文字语言与日常用语的区别；另一方面可以培养学生的读图、识图能力；同时，还在“润物细无声”中向学生渗透了分类讨论的思想。

同时，在课堂教学过程中，对于“三种语言”的教学，教师也可引导学生通过表格进行对比，让学生直观了解、一目了然，如在教学“线段的中点”与“角的平分线”这一课时，教师可引导学生通过表1进行对比。

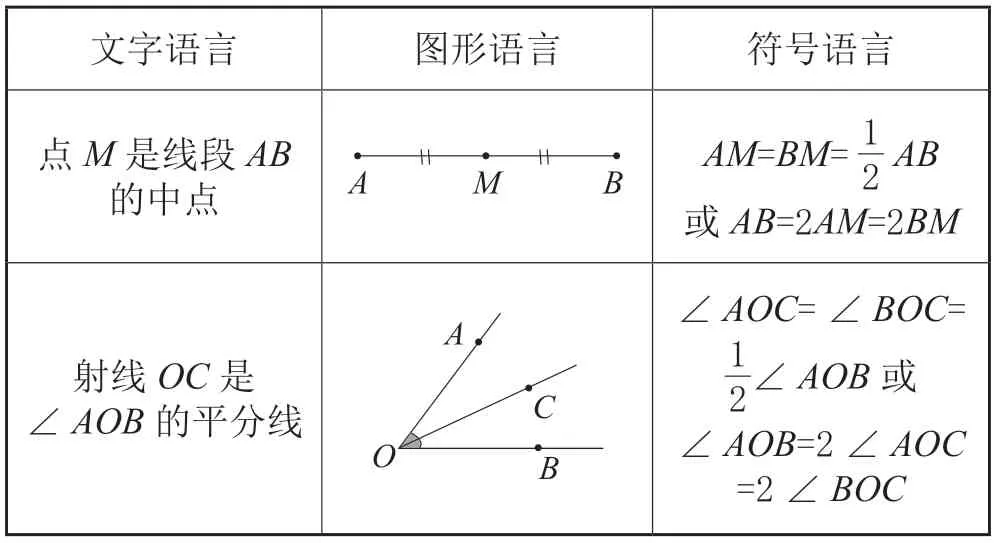
表1

在几何入门教学过程中，教师不仅要培养学生识图、读图、画图、作图的能力，还要锻炼学生对这三种数学语言之间的互换、互译能力，同时还要结合图形培养学生的看、说、画、写的能力。正所谓“‘文、图’化‘数’见精微、‘数、图’化‘文’揭内涵、‘文、数’化‘图’露本质。”

四、着眼核心素养，关注推理论证

七年级学生刚刚接触几何图形及三种语言的互译，教师如何熟练、准确、规范地引导学生学会运用几何的符号语言来推理、论证呢？这也是七年级学生学习几何的重要方面，教师应引起足够的关注与重视。

已知：如图4，点C是线段AB上一点，且AC= 5cm，BC＝3cm，若点D、E分别是线段AC、BC的中点，求线段DE的长。

图4

对上述问题，很多学生直接写出答案，这显然与数学学科核心素养中的“逻辑推理”的要求相差甚远。学生虽然理解了线段中点的定义与性质，但如果想用几何的符号语言进行准确表达、规范书写，就感觉比较困难。此时，教师要耐心地引导学生分析，细心地给学生示范，让学生规范地模仿与书写。因此，落实对学生数学学科核心素养的培养，打造灵动的课堂，可以让学生在几何的知识海洋中乘风破浪。