环境减灾二号A/B卫星基于加速度响应的运输环境疲劳分析

东巳宙 白照广 常静 邓卫华 扈勇强

(航天东方红卫星有限公司，北京 100094)

航天器运输一般采用公路、铁路、飞机3种运输方式，大型航天器由于整器尺寸超过这3种运输方式限制，如载人飞船等，往往采用海运的方式。运输环境是航天器全生命周期的一个重要组成部分，是其所经历的重要环境历程。航天器运输环境与发射环境不同，发射过程持续时间短，力学环境相对确定，并且可以通过正弦振动试验、随机振动试验、噪声试验来考核航天器对发射环境的适应性；但运输环境持续时间长，其力学环境受到路况、运输车辆状态、车辆速度、驾驶员驾驶能力等多方面影响变得极为复杂，整个过程无法通过力学试验进行准确模拟。因而对航天器在运输过程中所经历的力学环境进行分析，对产生的疲劳与损伤进行评价具有十分重要的意义。

剔除急刹车、天气环境骤变等卫星运输过程中的偶发事件，卫星的运输过程可以看作是一个平稳的随机振动环境。对随机振动环境下的产品进行疲劳分析的方法主要包括时域和频域两种。时域疲劳分析方法以采集的时域信号为数据源，进行应力循环次数统计，累计每次循环的损伤量作为损伤评价指标，时域疲劳分析法以雨流循环计数法最为典型。但由于时域分析方法计算量大，在工程应用中受到很大限制。频域疲劳分析方法则是依据功率谱密度函数近似估计疲劳损伤，由于频域信号的获取相对更加简单，频域疲劳分析方法更有利于工程应用的开展，因而基于频域疲劳损伤分析受到广泛关注。

文献[1]通过引入疲劳影响因子，对3σ截断后的疲劳损伤影响进行评价，并以典型实测呈高斯分布特征的应变数据为基础，对Wirsching and Light方法、α0.75方法、TB1和TB2方法[2-3]进行了对比分析。文献[4]以Miner线性累计损伤理论为基础，通过动力学仿真计算得到包装结构的应力、响应，结合材料S-N曲线以及疲劳累计分析对包装结构疲劳损伤进行了评价。文献[5]通过Lalanne逆变换对实测相对位移数据处理得到功率谱密度(PSD)谱，基于Dirlik函数[6]、Miner线性累计损伤理论采用有限元方法对转向架水平梁模型进行随机振动疲劳分析。文献[7]以高斯三区间法、Miner线性损伤累计理论为基础，通过对Ansys软件进行二次开发，实现了随机振动疲劳[8]寿命可视化。文献[9]针对电子设备进行了频域疲劳分析方法建立，并结合电子设备随机振动损伤实例验证了该方法的合理性。文献[10]对某航天器结构进行了频响计算，通过设定不同采样步长及采样初始频率，对结构敏感位置时域仿真数据进行了提取，通过疲劳法分析，对不同采样步长及采样初始频率下的损伤结果进行了对比。文献[11]基于Minert线性累计损伤原理、Dirlik幅值概率密度函数通过有限元分析计算得到了某机载产品疲劳损伤，分析结果与试验结果一致。文献[12]从正弦响应及加速寿命试验的角度对卫星运输过程中的累积疲劳损伤进行了简单介绍。

综上所述，频域疲劳损伤的分析方法以Miner线性累计损伤理论为主，结合结构应力-疲劳寿命(S-N)曲线，对结构应力累计损伤进行统计，进而对结构破坏进行评价。然而该方法评价的基础是S-N疲劳循环曲线，对于复杂的卫星结构，很难通过疲劳试验获取该数据。卫星结构安全裕度考核的方法是鉴定级振动试验，该试验往往是在验收级振动试验量级的基础上增加一定倍数作为结构安全裕度考核的依据，并且振动试验过程中以加速度传感器进行测量，对频域响应数据进行分析。针对这一问题，本文从Miner线性疲劳累计损伤分析方法出发，构建了基于加速度响应的运输环境疲劳分析方法。

1 疲劳分析理论与方法

1.1 基于Miner法则的疲劳分析方法

Miner法则[13]将疲劳累计损伤线性假设如式(1)所示。

(1)

式中:ni表示结构在应力幅值为Si时所经历的循环次数；Ni表示结构在应力幅值Si下的疲劳寿命；Ni与Si对应关系通过S-N曲线获取。当累积损伤D达到1时，认为结构会发生失效。

结构及材料的实际累计损伤值与其规格尺寸、加工工艺、载荷量级加载的顺序等因素相关。Miner法则的理论基础则是对复杂疲劳损伤的一种简化：①疲劳损伤与历经循环荷载成线性正比关系[14]；②结构及材料累计损伤破坏过程是其历经循环加载后吸收能量达到其上限的结果；③疲劳损伤全周期中的每一次加载均可单独计算损伤，最后每一次损伤值线性累加得到疲劳损伤全周期数值。

卫星运输可以认为是一个持续过程，其应力分布为连续状态，在时间T内应力范围(Si,Si+ΔSi)下的应力循环次数[15]为

ni=νTP(Si)ΔSi

(2)

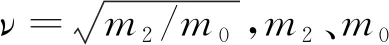
谱矩往往用来描述平稳随机过程中功率谱密度的统计特征，第j阶谱矩的定义如式(3)所示。

(3)

式中：f为频率；G(f)为单边功率谱密度。

将式(2)代入式(1)可以得到时间T内连续分布应力状态下的疲劳损伤值D。

(4)

式中：S为应力变量。

当结构发生疲劳破坏时，即D=1，结构疲劳寿命[16]为

(5)

1.2 高斯三区间法

高斯三区间法是一种随机振动疲劳损伤分析的频域方法，首先将随机响应的整个应力区间按照±σ、±2σ、±3σ分成了3个区间，然后分别计算各个阶段的疲劳损伤值，最后线性叠加得到结构的累计疲劳损伤。高斯三区间法认为应力响应在三区间中占比分别为68.3%、27.1%、4.33%，总占比达99.7%，大于3σ应力值的概率可以忽略。

时间t内，结构在三区间内的应力损伤分别为

(6)

(7)

(8)

式中：N1σ、N2σ、N3σ分别为根据材料疲劳曲线查得结构在3个应力区间所能承受的疲劳循环次数。

将式(6)～式(8)代入式(1)得到结构疲劳损伤累计计算公式为

(9)

进一步根据Miner法则，D=1时，结构发生疲劳破坏，由式(9)可以得到结构疲劳寿命时间[15]为

(10)

2 卫星公路运输随机振动应力疲劳分析

卫星运输过程中采用数据采集系统实时监测卫星运输环境，如图1所示。振动传感器粘贴于包装箱内部减振器上方，采集方式为触发采集，触发量级为0.4gn，采样频率1024 Hz。卫星运输环境与车速、路况、司机操作熟练程度有很大关系，卫星运输过程中严格控制车辆速度，在运输过程中保持不高于30 km/h速度行驶。下文将从卫星公路运输过程中采集到的频域响应出发，对卫星运输过程中产生的疲劳损伤进行分析。由于在运输过程中卫星Z向响应较大，因而本文只对卫星运输过程中的Z向响应进行疲劳分析。

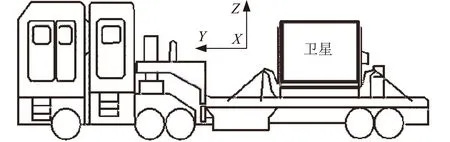
图1 卫星运输环境监测系统示意图Fig.1 Schematic diagram of monitoring system of satellite transportation environment

2.1 运输数据频谱分析

对卫星运输过程中采集的时域信号进行频谱分析，得到所有触发采集信号的功率谱密度曲线(PSD)及其响应包络曲线，如图2所示。

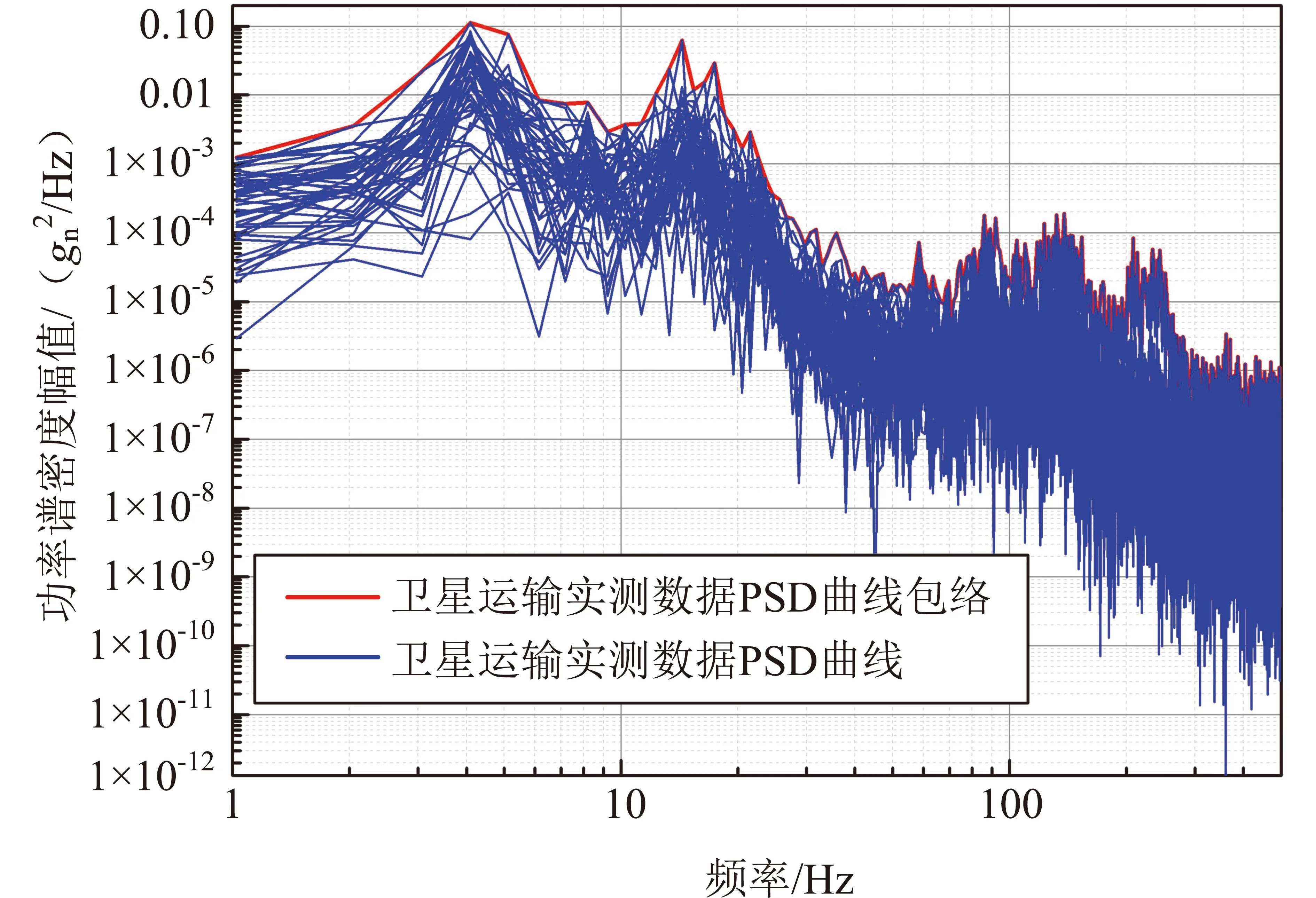
图2 卫星运输环境功率谱密度曲线Fig.2 Power spectrum density curves of satellite transportation environment

由图2分析可知：卫星-弹簧系统共振频率分别为4 Hz、14 Hz，远低于卫星固支边界下共振频率；卫星在减振系统作用下，响应峰值为0.11gn2/Hz，出现在颠簸路段；较大响应出现在低频段，高于30 Hz频段处响应仅约为1.9×10-4gn2/Hz，远低于卫星随机振动输入条件在此频段的量级0.04gn2/Hz。

2.2 随机载荷激励下卫星应力分析

基于卫星运输频域数据包络曲线，采用模态叠加法[17]对卫星进行随机响应分析，获得卫星平台舱主结构应力云图，如图3所示。

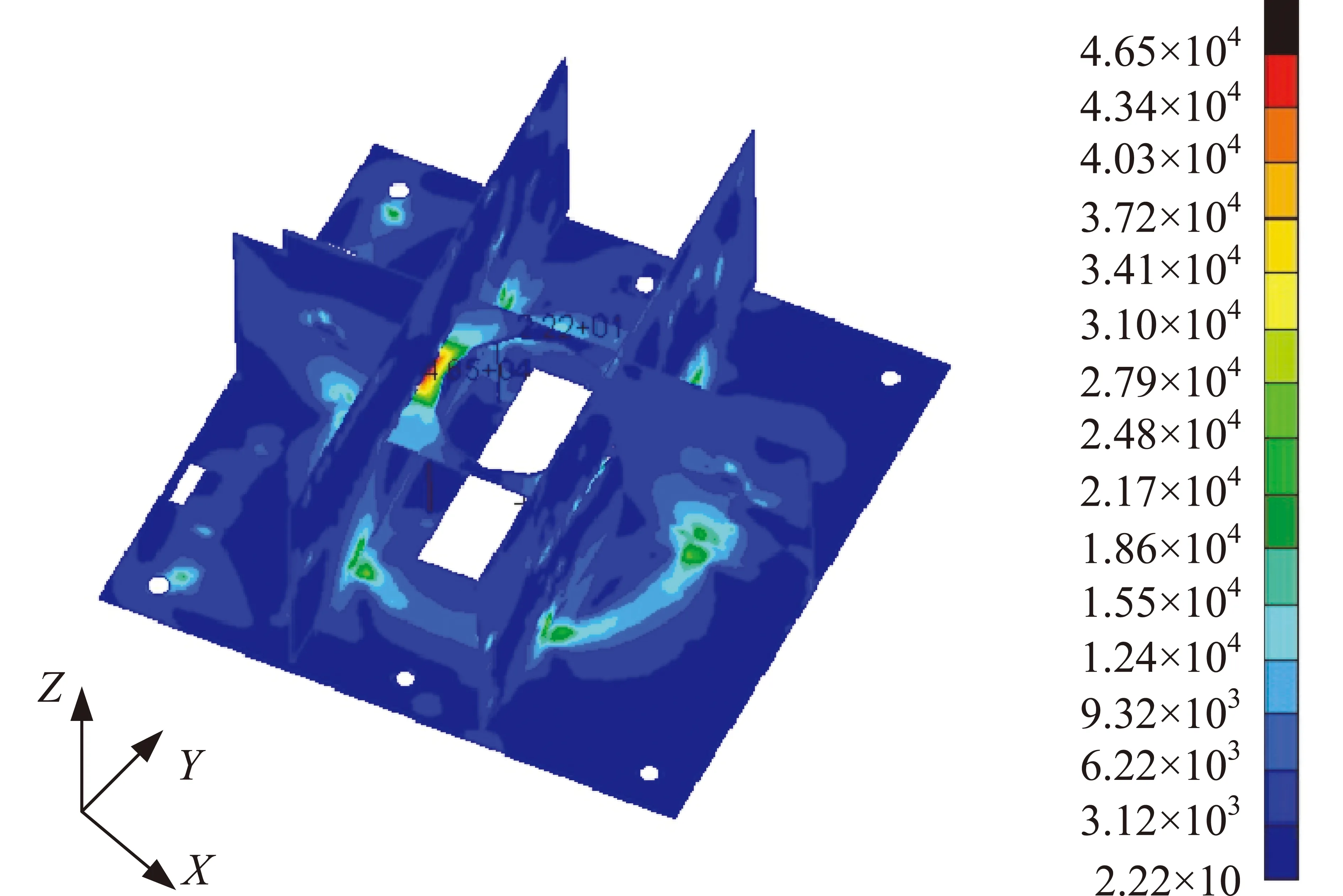
图3 卫星平台舱主结构应力云图Fig.3 Stress contour of satellite platform

从图3中可以看出：卫星主结构1σ应力最大为0.046 5 MPa，进而可以按照线性计算得出2σ、3σ应力，分别为0.093 MPa、0.139 5 MPa，由三区间法可知，大于3σ的应力只发生在(100×0.27%)～(99.7×0.27%)[2]的时间内，对结构损伤可以忽略。

2.3 随机振动应力疲劳分析

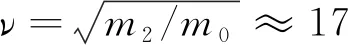
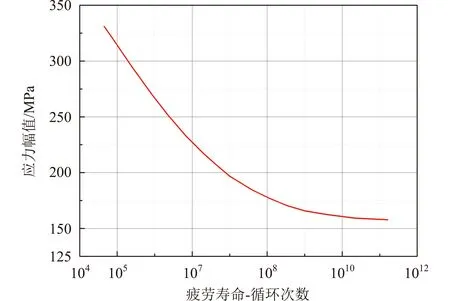
图4 结构板应力疲劳曲线Fig.4 Structural plate stress fatigue curve

卫星在公路运输过程中受到的最终疲劳损伤值约为0，由Miner法则可知，当D值为1时，结构发生破坏，由此可以认为公路运输过程，卫星结构没有发生损伤，运输环境对卫星结构无影响，卫星包装箱减振系统起到了较好的减振效果，保证了卫星运输环境的稳定性。

3 卫星公路运输正弦振动应力疲劳分析

3.1 运输数据冲击响应谱分析

对卫星运输过程中采集的时域数据进行冲击响应谱分析，得到所有触发采集信号的冲击响应谱曲线(SRS)及其包络曲线，如图5所示。

图5 卫星运输过程冲击响应谱曲线Fig.5 Shock response spectrum curve during satellite transportation

由图5中数据可以看出：卫星-弹簧系统共振频率分别为4 Hz、14 Hz，这与PSD频谱分析结果一致；卫星在减振系统作用下，响应峰值为0.35gn，出现时刻与PSD频谱分析结果一致；较大响应出现在低频段，高于30 Hz频段处响应仅约为0.15gn，低于卫星正弦特征级输入条件在此频段的量级0.2gn。

3.2 正弦载荷激励下卫星应力分析

以图5包络得到的冲击响应谱作为输入，对卫星进行正弦响应分析，得到卫星平台舱主结构应力云图，如图6所示。

由图6可知卫星主结构最大应力所在位置与图3中一致，均出现在储箱安装板与卫星长隔板的连接处，最大应力为1.61 MPa；其他应力较大位置出现在隔板与底板的连接处，以及对接环与底板连接位置。

图6 正弦载荷作用下卫星平台舱主结构应力云图Fig.6 Stress contour of satellite platform under sinusoidal load

3.3 正弦振动应力疲劳分析

卫星在运输过程中数据采集系统共采集32组数据，即进行了32次触发采集，触发量级设置为0.4gn，认为小于0.4gn的环境对卫星没有产生任何影响。假定采集的32组数据均为最大响应量级，即卫星共经历32次图5中最大冲击响应谱包络的环境，产生了32次1.61 MPa的应力。结合结构应力最大位置处疲劳寿命曲线(见图4)，基于Miner法则式(1)，得到卫星结构板应力疲劳损伤累计疲劳损伤值D≈0，这与3.3节中随机振动应力疲劳分析结果一致。

4 基于加速度响应疲劳分析

现有疲劳分析方法均是首先通过测量得到的应变或应力量级以及响应循环次数，然后通过查询相应结构材料的疲劳寿命曲线，最后结合实测数据以及查询的寿命曲线通过不同方法得到结构的疲劳寿命评估结果。然而在卫星运输过程中更便于以加速度传感器测量的方式对运输环境进行监测评估，因此，本文将基于卫星运输环境实测加速度响应，对卫星结构疲劳进行分析。

卫星整星级正弦振动试验、随机振动试验是卫星力学特性检验评估的依据，本文将分别以鉴定级正弦振动、鉴定级随机振动试验为卫星结构所能经受的极限量级，构建正弦振动加速度响应疲劳曲线、随机振动功率谱密度响应疲劳曲线；由于本文所研究的卫星运输环境较大响应出现在30 Hz以内的频段内，对低频段考核往往以正弦振动试验最为严苛，因此，本文将从正弦振动量级出发，对小于30 Hz之内的运输数据进行疲劳分析，对大于30 Hz的运输数据，则从随机振动量级出发进行疲劳分析。

4.1 加速度疲劳寿命关系建立

当结构经受持续振动载荷时，每个加载循环均会在结构材料内部产生损伤，当损伤量累积到一定程度，结构即发生破坏。对于不同的结构往往通过试验得到相应疲劳寿命曲线，该曲线往往表征实测应力值与该应力值导致结构破坏的循环次数之间关系。式(11)即典型疲劳寿命关系式。

NSb=C

(11)

式中：N表示结构在应力幅值SSi下的疲劳寿命；S为应力幅值；b为常数，其取值受材料、结构形式等的影响；C为常数。

振动响应量级与应力之间存在一定关系，响应量级越大，结构产生的应力越大，因此加速度疲劳寿命曲线可以基于式(11)进行表征，而卫星结构考核往往以鉴定级振动试验通过为依据。因而本文将假定以鉴定级振动试验量级作为卫星结构破坏的参量，认为卫星经历一次鉴定级振动试验即发生破坏。在卫星研制生产过程中，以验收级振动试验作为卫星结构环境适应性的考核，而正弦鉴定量级往往是验收量级的1.5倍，随机鉴定量级功率谱密度是验收量级的2倍，如式(12)、式(13)所示。

(12)

(13)

式中：W为随机振动响应幅值(单位为g2/Hz)；g为正弦振动响应幅值(单位为g)；T为持续时间；下标jdj表示鉴定级试验、ysj表示验收级试验。

美国军用标准MIL-STD-810F[18]对不同量级振动疲劳损伤进行了等效，用以描述时间与振动量级之间的疲劳等效关系。式(14)、式(15)分别描述了随机振动响应幅值、正弦振动响应幅值与累计时间的关系。

(14)

(15)

将式(12)代入式(14)即可得到验收级随机振动试验与鉴定级疲劳损伤等效时间之比T1/T0=16，将式(13)代入式(15)即可得到验收级正弦振动试验与鉴定级疲劳损伤等效时间之比T1/T0=11.39。由于鉴定级振动试验持续时间是验收级的2倍，而假设产品经历1次鉴定级振动试验产品即发生破坏，因此可以得到产品经历32次验收级随机振动试验发生破坏，经历23次验收级正弦振动试验发生破坏。进而得到随机振动加速度响应幅值-疲劳寿命(A-N)曲线的两对数值(Wjdj,1)(Wysj,32)，正弦振动加速度疲劳A-N曲线的两对数值(gjdj,1)(gysj,23)，分别代入式(11)，即可得到随机振动加速度疲劳A-N曲线，如式(16)、正弦振动加速度疲劳A-N曲线，如式(17)所示。

(16)

(17)

4.2 基于正弦加速度响应疲劳分析

本文所研究的卫星可以承受的正弦鉴定试验量级为0.9gn，该量级是经过结构星振动试验验证的最大量级，因此，由式(17)可以得到本文所研究卫星的正弦振动累计损伤疲劳模型，如图7所示。

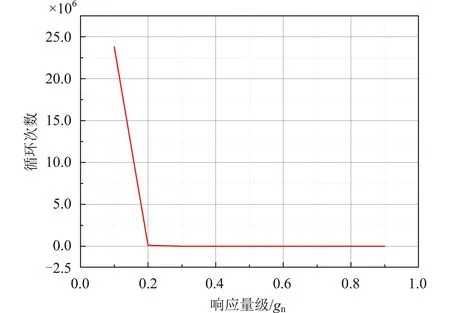
图7 卫星正弦振动加速度疲劳A-N曲线Fig.7 Satellite sinusoidal vibration acceleration fatigue A-N curve

根据卫星运输环境实测数据冲击响应谱分析结果，卫星运输过程所经历最大量级为0.37gn，可以假定采集的32组数据最大量级均为0.37gn，结合图7中数据，可得出0.37gn对应卫星疲劳寿命为964次，进而结合Miner法则可以得到卫星在低频段的疲劳损伤累计疲劳损伤值D≈0，进而可以得出运输环境低频段对卫星结构无影响的结论。

4.3 基于随机功率谱密度响应疲劳分析

本文所研究的卫星可以承受的随机鉴定试验量级为0.08gn2/Hz，该量级是经过结构星振动试验验证的最大量级，因此，由式(16)可以得到随机振动功率谱密度响应疲劳A-N曲线，如图8所示。

根据卫星运输环境实测数据PSD频谱分析结果，30 Hz以上频段，卫星运输过程所经历最大量级为3×10-4gn2/Hz，可以假定采集的32组数据在该频段最大量级均为3×10-4gn2/Hz，结合图8中曲线，可得出响应量级为3×10-4gn2/Hz对应的卫星疲劳寿命为1.4×1012次，进而结合Miner法则可以得到卫星在30 Hz以上频段的疲劳损伤累计值D≈0，该频段运输环境对卫星结构无影响。

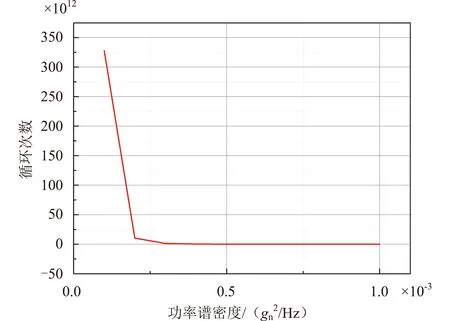
图8 卫星随机振动功率谱密度响应疲劳A-N曲线Fig.8 Satellite random vibration power spectrum density response fatigue A-N curve

5 结果分析

将随机振动应力疲劳分析、正弦振动应力疲劳分析以及基于加速度响应的疲劳分析结果进行统计，见表1。

表1 卫星疲劳寿命评估结果Table 1 Satellite fatigue life assessment results

由表1中数据可以得出：①3种分析方法所得到的疲劳累计损伤值均为0，公路运输过程卫星结构没有发生损伤，运输环境对卫星结构无影响；②基于应力疲劳分析方法计算得到的卫星运输环境累计损伤为0，而基于加速度响应疲劳分析得到的结果要大于基于应力分析结果，尤其基于正弦加速度响应疲劳分析结果相对其他分析结果更为保守，因此在进行卫星运输环境疲劳分析时，可以优先采用本文所探讨的基于加速度响应疲劳分析方法进行保守计算。

6 环境减灾二号A/B卫星运输环境疲劳分析

为了对基于加速度响应的卫星运输环境疲劳分析方法进行进一步的验证，本文以环境减灾二号A/B卫星在运输过程中最为恶劣的方向轴向(X向)为例进行说明。

环境减灾二号A/B卫星可以承受的纵向正弦鉴定试验量级为1.2gn，该量级是卫星在设计过程中所保证的卫星能够经受的最大量级，卫星在实际试验过程中经历的考核量级为0.8gn验收级，因此，由式(17)可以得到本文所研究卫星的正弦振动加速度响应疲劳分析模型，如图9所示。

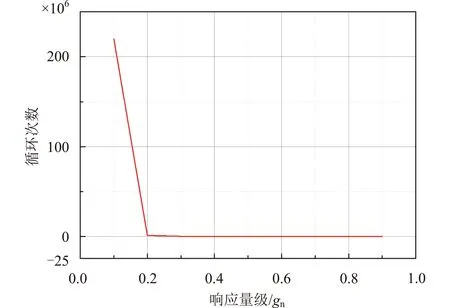
图9 环境减灾二号A/B卫星正弦振动加速度疲劳A-N曲线Fig.9 HJ-2A/B satellites sinusoidal vibration acceleration fatigue A-N curve

环境减灾二号A/B卫星在运输过程中采用触发采集的方式获取数据，触发量级为0.6gn，A星共采集54组数据、B星共采集7组数据，通过对数据进行冲击响应谱分析，得到了表2的分析结果。

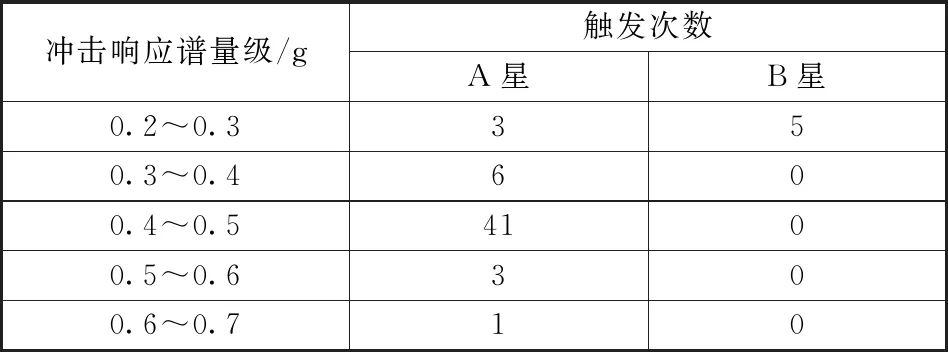
表2 HJ-2A/B卫星冲击响应数据统计结果Table 2 Statistical results of HJ-2A/B satellites impact response data

基于Miner法则，结合表2中数据，可以得到环境减灾二号A/B卫星在低频段的疲劳损伤累计疲劳损伤值D分别为：A星D=0.078，B星D=1.11×10-4。因此可以得出环境减灾二号A/B卫星在运输环境下没有受到影响，同时结合卫星能够在轨正常工作，也可以说明这一点。

7 结论

本文基于Miner线性疲劳累计损伤分析方法，分别从随机振动应力疲劳分析、正弦振动应力疲劳分析、加速度响应疲劳分析3个角度出发对卫星在公路运输环境下的疲劳损伤进行了评估，建立了评估卫星疲劳损伤的加速度疲劳寿命关系，并以环境减灾二号A/B卫星运输环境数据为实例，从正弦加速度响应出发对卫星的疲劳寿命进行了评估。通过本文疲劳寿命分析可以得出以下结论：

(1)卫星-弹簧系统的共振频率集中在低频段；

(2)卫星正弦振动分析得到的应力大于随机振动分析得到的3σ应力；

(3)卫星运输环境疲劳寿命可以通过测得的加速度响应数据进行评估，低频数据以正弦加速度响应进行疲劳分析，中高频数据以随机功率谱密度响应进行疲劳分析；

(4)卫星在公路运输过程中以30 km/h的行驶速度前行，所产生的运输环境未对卫星结构产生疲劳损伤。