一种冷热交变环境下太阳帆应力保持方法

王 杰，聂云清，吴 军，刘 望，袁 福，邹 杰

(国防科技大学空天科学学院，长沙 410073)

0 引 言

太阳帆航天器利用太阳光压作为驱动力实现宇宙航行，是一种先进的无工质推进航天器，在高轨、深空等长航时探测任务中具有显著优越性。

随着大型空间结构可展开技术以及大面积轻质薄膜技术的发展，世界上主要国家和机构纷纷开展太阳帆航天器的研究。德国宇航中心(DLR)于1999年首次开展了太阳帆的地面展开试验。日本宇宙航空研究开发机构(JAXA)于2010年成功发射了世界上第一个太阳帆航天器IKAROS，验证了光压推进技术完成深空探测任务的可行性。美国国家航空航天局(NASA)于2011年发射了太阳帆NanoSail-D2，验证了太阳帆在轨展开技术和加速离轨功能。美国行星协会于2015年和2019年成功发射了LightSail-1和LightSail-2，验证了太阳帆在轨展开技术、采用立方星作为载荷的可靠性以及姿态控制功能。英国萨里大学依托QB50计划，于2017年成功发射了InflateSail，验证了近地轨道的离轨功能。下一步，美、日、德等国致力于研制面质比更大的太阳帆航天器以进行小行星探测、深空探测、近地轨道碎片清除等任务。我国相关研究机构和大学也较早开展了太阳帆航天器关键技术的论证，针对轨道保持和控制、轨道和姿态控制、自旋展开控制、结构动力学与控制、热致动力学分析和太阳帆展开地面试验等关键技术开展了广泛的研究。清华大学Gong等对太阳帆的发展史及涉及的关键技术(轨道设计、姿态控制、结构动力学等)及现状进行了综述。

太阳帆航天器利用帆面反射太阳光子获得的动量对航天器进行加速，为尽可能获取较大的加速度，帆面采用轻质薄膜，同时需要尽可能大，以提高航天器的面质比。由于发射时火箭包络的限制，国内外主要提出和发展了两类展开方式的太阳帆航天器。一类是利用轻质支撑杆支撑大面积薄膜，在轨时通过电机、充气或应变能驱动支撑杆展开，形成航天器的飞行构型。一类是自旋式展开，在薄膜顶端布置集中质量，利用离心力牵引薄膜展开，在轨时航天器通过自旋保持平面。

为获取较大的光压，薄膜尽可能避免褶皱等变形，因此展开后薄膜内部需具备一定的预应力。然而，对于支撑杆式太阳帆，在轨经历高低温交变时，薄膜与支撑杆由于热膨胀系数的不一致，薄膜内部的应力将发生变化，一方面将造成薄膜形面发生位移，导致光压发生改变；另一方面可能导致薄膜松弛或内部应力过大，造成薄膜撕裂、支撑杆屈曲等危害航天器寿命的结果。NASA太阳帆研究对比了支撑杆采用合金和碳纤维两种材料时，在经历高低温时，支撑杆压力的变化。采用碳纤维支撑杆时，标称压力1.4 N，当热载荷作用时，压力增加了70%，极易造成支撑杆屈曲。

连接单元用于连接支撑杆和轻质薄膜，并对薄膜施加预应力，是太阳帆航天器研制中的关键技术之一，欧空局将其与展开机构、薄膜材料、太阳帆地面试验并列为4大亟待突破的技术。IKAROS是自旋式太阳帆，依靠顶端质量块的离心力以绳索牵扯薄膜使其保持平面。德国Gossamer-1太阳帆地面验证系统采用绳索连接豆荚杆与薄膜，而地面验证系统无需考虑高低温变化的影响。美国NASA太阳帆地面研制项目中，ATK公司和L’Garde公司分别研制了尺寸为20 m的太阳帆并开展了地面展开实验。ATK公司太阳帆设计采用了找形分析方法以保证帆面平整，通过恒力弹簧连接盘绕式桁架和聚酰亚胺薄膜。然而采用找形分析的方法导致帆面有效面积减小，填充因子仅82.5%。此外，为避免在帆面展开过程、大角度姿态机动或太阳帆进入地影区等导致的极端热变形中帆面应力过大，桁架与薄膜之间增加了跳线带(Jumper strap)，文献未给出在轨帆面应力变化范围。L’Garde公司以充气杆为支撑杆，采用Kevlar绳索连接支撑杆和帆面。NanoSail-D2和LightSail-1太阳帆均采用线性伸缩弹簧连接支撑杆和薄膜。而在LightSail-2太阳帆在轨试验中，由于支撑杆的结构失效或热致扭转变形，支撑杆发生了非线性弯曲。NASA小行星探测太阳帆的仿真结果表明高温情况下薄膜比支撑杆多膨胀2.9 cm，在采用线性伸缩弹簧进行设计时，为使弹簧在较大的长度变化时拉力变化较小，弹簧设计长度需较大，造成薄膜面积减小。之后提出了采用恒力弹簧作为连接单元的方案，采用恒力弹簧，薄膜应力在轨变化保持在设计应力±5%的范围内。然而，恒力弹簧的刚度非线性导致系统刚度较低。上述Kevlar绳索、线性伸缩弹簧或恒力弹簧连接方案仍具有未考虑应力变化、弹簧长度、系统刚度等局限性。因此，在高低温交变载荷下太阳帆薄膜应力保持成为该领域亟需解决的问题。

连接单元需具备以下功能：1)在轨高低温作用下使薄膜基本保持恒定应力；2)有效降低褶皱发生的可能性，减小褶皱的区域；3)有效避免支撑杆发生屈曲；4)由于机械制造误差等因素，薄膜应力设计状态与实际状态有区别，连接单元需要具备一定的鲁棒性，控制薄膜应力在一定的范围内。

本文基于形状记忆合金(SMA)弹簧提出了一种太阳帆张拉设计方法，可使航天器在经历高低温变化时薄膜应力保持恒定。该方法采用形状记忆合金弹簧补偿薄膜和支撑杆之间的间隙变化：当航天器由高温进入低温时，薄膜和支撑杆间隙变大，同时形状记忆合金弹簧刚度减小，弹簧伸长；而当由低温进入高温时，薄膜和支撑杆间隙减小，同时形状记忆合金弹簧刚度增大，弹簧缩短。因此，形状记忆合金弹簧在提供额定拉力的同时，可有效适应薄膜与支撑杆之间的间隙变化。

1 太阳帆构型介绍及问题描述

本文中所研究太阳帆如图1所示。太阳帆在轨展开构型为正六边形，边长为7 m。太阳帆主要由星体、支撑杆和帆面组成，其中星体位于正六边形的中心，支撑杆共6根，根部均固定在星体上。太阳帆帆面由6块梯形薄膜组成，每块梯形薄膜由星体和支撑杆张紧。在梯形薄膜远端(即支撑杆顶端)和根部(靠近航天器星体处)，通过连接单元与支撑杆连接。太阳帆在发射时，在运载火箭内部处于收拢状态，每根支撑杆卷绕在一起，每块梯形薄膜通过Z字形折叠和卷绕收拢。

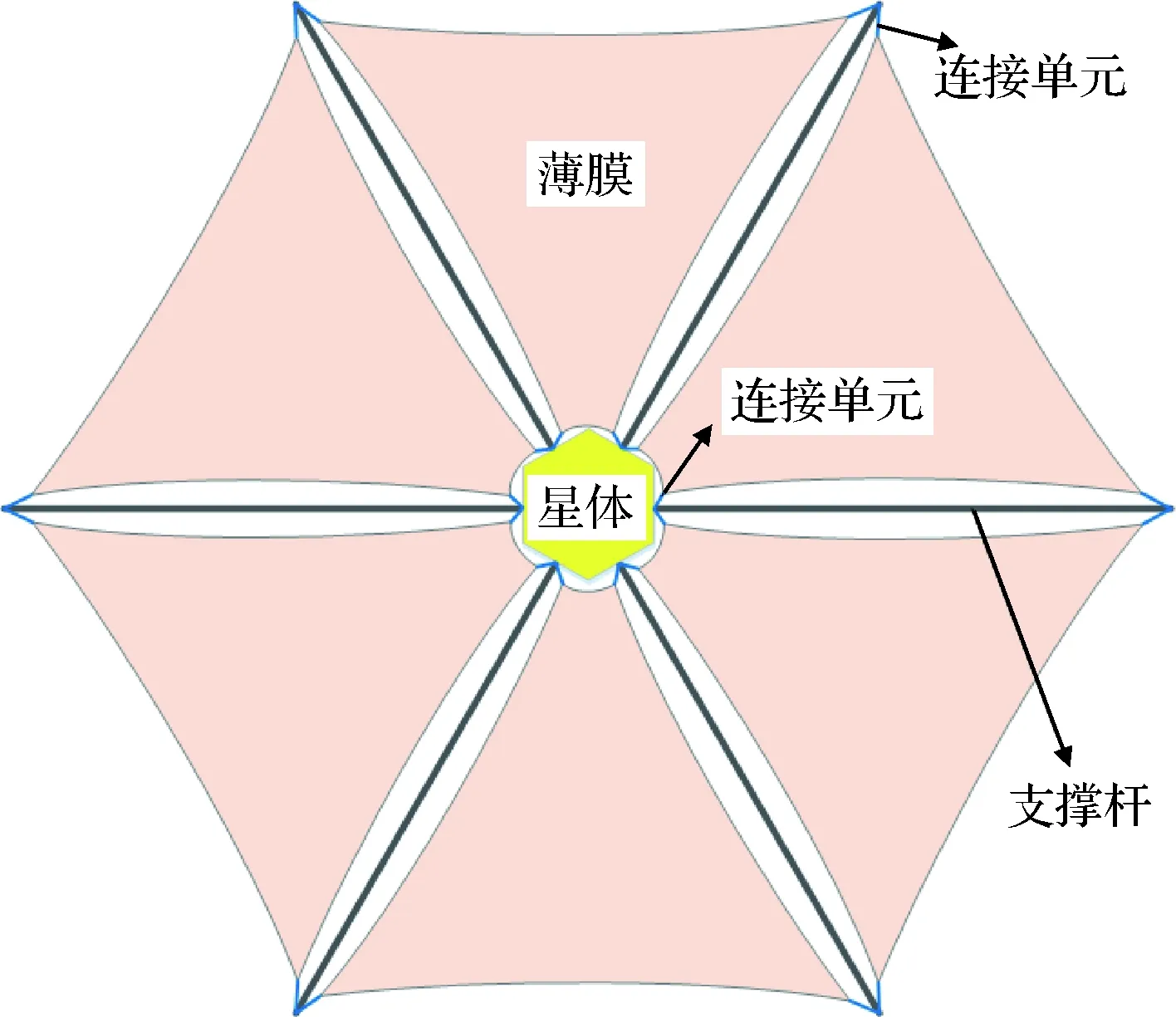
图1 太阳帆构型示意图

支撑杆为豆荚杆，由碳纤维/环氧树脂预浸料材料层合制作而成。薄膜材料为正面(即面向太阳一面)镀铝聚酰亚胺。为保证薄膜在轨尽可能保持平面,以最大程度利用太阳光产生光压，太阳帆在轨时薄膜内部有一定的预应力，对支撑杆产生一定的预压力。另一方面，支撑杆为大长细比结构，当承受薄膜的预压力过大时，易发生屈曲。因此，综合考虑薄膜中心处预应力设置为6.90 kPa。

然而，太阳帆在轨温度变化时，支撑杆与薄膜温度变化和热膨胀系数不一致，导致薄膜应力发生变化。一般情况下，碳纤维为零膨胀或负膨胀系数，而聚酰亚胺膨胀系数达2×10K。若按照太阳直射状态时的薄膜、支撑杆温度场和热变形状态设计薄膜的应力，则当太阳帆进入地影区或航天器姿态发生变化导致温度急剧降低时，薄膜热致收缩远大于支撑杆，薄膜应力急剧增加，导致支撑杆发生屈曲。反之，若按照太阳帆处于低温时的状态设计薄膜的应力，则当太阳帆温度急剧升高时，薄膜热致膨胀大于支撑杆，薄膜应力减小，甚至发生松弛现象。

2 太阳帆张拉方法

针对高低温变化导致薄膜应力发生大范围变化的难题，本节中提出了一种基于形状记忆合金弹簧的太阳帆张拉方法，利用高低温下形状记忆合金的非线性特性，进行迭代设计以保证太阳帆在高低温状态下薄膜应力在一定的范围内变化。

2.1 张拉方案

薄膜张拉方法如图2所示，该图为太阳帆1/6模型，包括星体、两根支撑杆和一块薄膜，薄膜为一个等腰梯形结构。图2中，太阳帆航天器本体外表面固定有支撑杆，支撑杆的顶端还设有用于牢固夹住支撑杆的固定环机构，薄膜需要通过一定的张拉方式连接到支撑杆固定结构和固定环机构上。在薄膜的四个角点A,B,C和D处，还布置有4个金属扣环，其中A点和D点位于薄膜的根部，B点和C点位于薄膜的顶端。在薄膜顶端B点和C点，通过由Kevlar绳和形状记忆合金弹簧构成的连接单元与支撑杆上的固定环机构连接。在薄膜根部A点和D点，通过由Kevlar绳和恒力弹簧构成的连接单元与太阳帆星体上的支撑杆固定结构连接。

图2 薄膜张拉方案示意图(非比例绘制)

形状记忆合金弹簧具有刚度非线性的特点，其加载示意图如图3所示。高温下(受太阳直射时)弹簧缩短，刚度系数增加;低温下弹簧伸长，刚度系数减小。形状记忆合金弹簧的刚度非线性，可有效补偿薄膜与支撑杆之间由于高低温导致的间隙变化。

图3 形状记忆合金弹簧加载曲线示意图

2.2 设计流程

根据高低温下薄膜与支撑杆间的间隙变化确定连接单元的参数，其设计流程如图4所示。

图4 连接单元参数确定流程示意图

首先基于有限元法建立太阳帆的热分析模型和力学分析模型；根据太阳帆的构型、轨道姿态特点，确定薄膜和支撑杆的高温工况和低温工况，基于热分析模型计算两种工况下的温度场；基于力学分析模型计算薄膜和支撑杆在高温和低温温度场下的热变形；根据两种工况下薄膜和支撑杆的变形之差，确定薄膜与支撑杆的连接单元的参数，包括形状记忆合金弹簧和恒力弹簧的参数。

2.3 形状记忆合金弹簧设计方法

形状记忆合金弹簧中，包括金属弹簧和形状记忆合金两个核心部件，均为螺旋式结构，并用外壳包装，参见图5。弹簧由形状记忆合金提供预紧力，金属弹簧仅起到一个辅助连接的作用，因此设计金属弹簧的刚度远小于形状记忆合金，使得在间隙变化过程中，金属弹簧的作用力变化与形状记忆合金相比，可以忽略。该形状记忆合金弹簧利用形状记忆合金的压缩性能，延缓了形状记忆合金的滞回效应，增加了使用寿命。采用外壳包装主要进行限位，避免由于金属弹簧断裂造成结构破坏。

图5 形状记忆合金弹簧构型示意图

形状记忆合金弹簧参数采用切弹性模量法，流程如下：

1)对于典型的形状记忆合金材料，高低温工况下的剪切模量分别为和；

2)根据薄膜静力分析结果，确定形状记忆合金弹簧承受的拉力；

3)根据支撑杆和薄膜的热变形分析结果，确定高温工况和低温工况下弹簧的行程差；

4)依据设计寿命取低温工况下最大切应变为，则可得到高温工况下最大切应变为

=

(1)

高温工况下最大切应力为

=

(2)

5)选取典型弹簧指数，簧丝直径为

(3)

式中:为低温工况下最大切应力。簧丝中径为

=π(8)

(4)

弹簧匝数为

(5)

高温工况和低温工况下弹簧刚度系数为

(6)

至此可得到形状记忆合金弹簧的全部参数。

为使形状记忆合金弹簧满足相变温度要求，弹簧外壳设计成镂空结构。弹簧外壳等其他结构采用导热系数低的材料制备，以减小支撑杆、薄膜与形状记忆合金丝间的导热。同时合金丝表面涂覆高吸收发射比涂层，使其稳态温度满足低温工况下低于相变温度、高温工况下高于相变温度的要求。

3 太阳帆温度场与热变形分析

本节首先建立太阳帆的热分析和结构动力学模型，然后根据轨道和姿态确定高温工况和低温工况，获取薄膜和支撑杆在轨运行时的温度场分布，最后计算得到太阳帆在高温和低温下的结构变形。

3.1 热变形分析有限元方法

航天器在轨运行时，热传导和热辐射是主要的热量传递方式。对于空间结构的辐射传导系统，根据傅立叶热传导定律和热力学第一定律，瞬态温度(,,,)可由下式给出

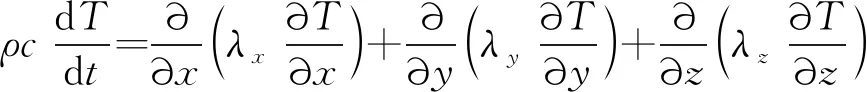
(7)

式中:为比热容，为密度，,和分别为,和向的热传导系数。边界条件可表示为

(8)

式中:,,为结构表面外法线的方向余弦，为内热源，为构件间热辐射，为轨道外热流，可表示为

=+++

(9)

式中:为太阳辐射热流，为地球辐射热流，为地球反照热流，为结构与深冷空间热辐射热流。

将结构划分为多个单元，每个单元看作一控制体积，节点的热平衡方程为

in,+or,

(10)

式中:为节点的温度，为比热容，为质量，为节点和网络热辐射系数，为节点和热传导网络系数，为斯蒂芬-玻尔兹曼常数。

给定初始温度场(=0)，采用有限差分法求解整个微分方程组，可得结构的时变温度场。航天器在受辐射热之后，各部分温度不均匀，产生不同程度的热膨胀，因此产生热应力和热应变，使各节点发生位移，导致整个结构发生热变形。

结构热膨胀系数向量可表示为

=[,,,,,]

(11)

式中:为各方向热膨胀系数。温度引起的应变为

=(()-)=(-)

(12)

式中:()为结构温度，为参考温度，为单元温度，为温度插值函数。

温度载荷向量可表示为

(13)

式中:为单元序号，为单元总数，表示单元的区域，是几何矩阵，是弹性矩阵。

结构热致变形所满足的有限元方程

()=()

(14)

式中:为刚度矩阵，()为单元节点位移向量。

由式(14)可求出整体坐标系中的节点位移，局部坐标系中的节点位移可通过式(15)计算

=()

(15)

式中:为整体坐标系和局部坐标系的转换矩阵。

单元应力为

(16)

3.2 太阳帆热分析模型

对于由豆荚杆、薄膜组成的空间结构，发生变形的主要因素是空间热流引起的豆荚杆截面温度分布不均匀。因此对于太阳帆，豆荚杆的弯曲是结构发生总体变形的主要因素。在建模时做以下假定：

1)豆荚杆沿管壁厚的温差可以略去，仅考虑沿横截面周向的温差；

2)豆荚杆与薄膜之间的连接单元长度较短、热容较小、受辐射面积较小、吸收辐射热流较小，和豆荚杆、薄膜之间的热传导为其主要热流来源，因此初步热分析时在热有限元模型中略去连接单元；

3)太阳帆基本为平面轴对称结构，在中心处的航天器本体尺寸较小，可忽略航天器本体对豆荚杆、薄膜温度的影响，因此可建立1/6模型。

薄膜和支撑杆的热分析模型如图6所示。

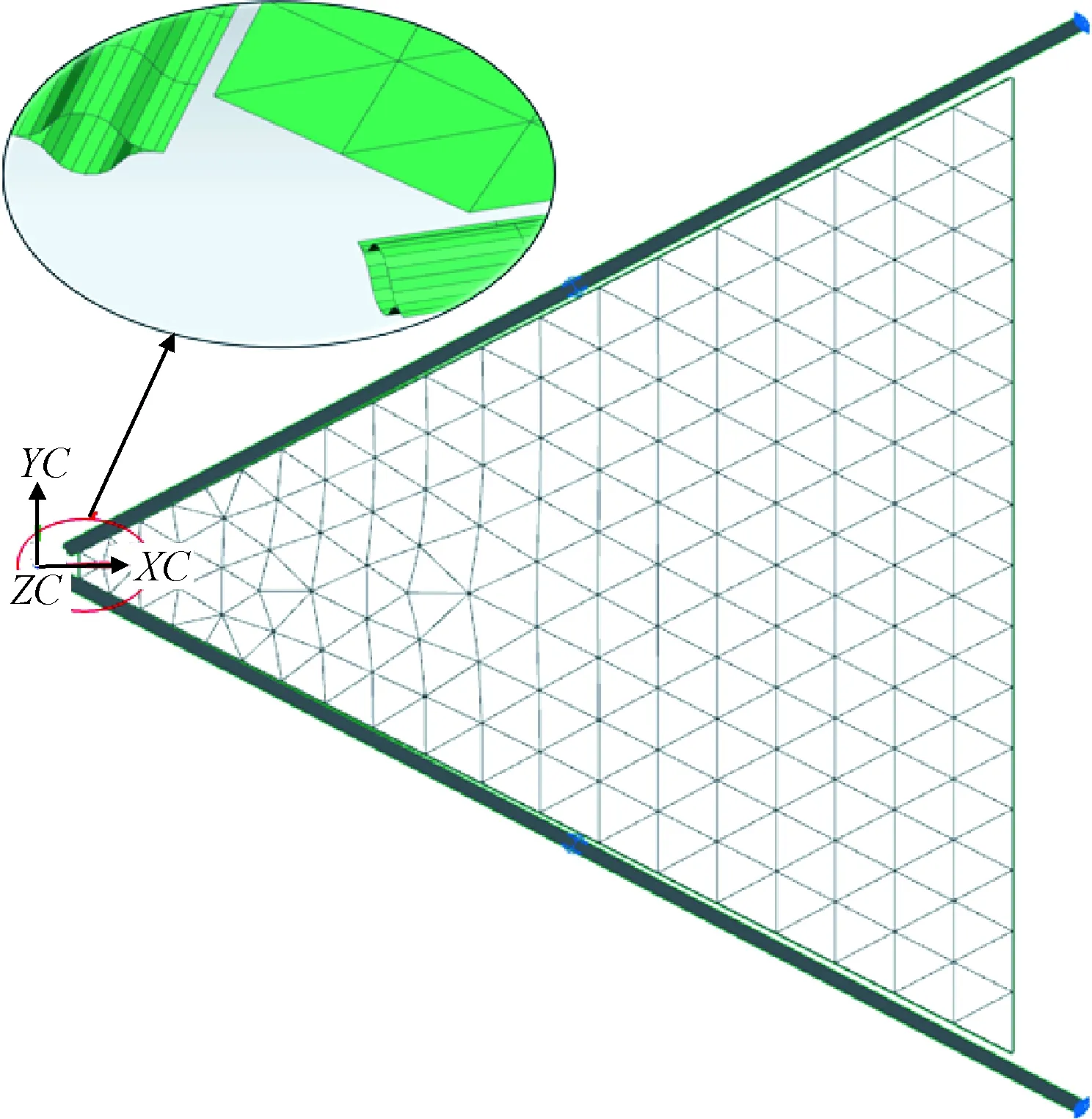
图6 太阳帆热分析模型

豆荚杆为碳纤维T300/LD180预浸料层合制作而成，单边豆荚杆铺层方式为45°/-45°/0°/-45°/45°，为对称铺层，每层厚度为0.04 mm，共计5层，总厚度0.2 mm。材料物性参数见表1。

表1 材料物性参数

注1. 0°表示沿纤维方向的参数，90°表示垂直纤维方向的参数。

注2. 镀铝表示聚酰亚胺表面镀铝(厚度0.1 μm)后的参数。

3.3 高低温工况分析与定义

航天器轨道为地球静止轨道，轨道周期为86400 s。每个运行周期内，可分为光照区和阴影区，光照区时间为82260 s，阴影区时间为4140 s，如图7所示。薄膜阵面的太阳入射角在0～90°的范围内，太阳入射角为0°时，薄膜始终保持对日状态，即轴指向太阳；太阳入射角为90°时，薄膜阵面法线垂直于太阳光方向。工况定义如下：

图7 薄膜航天器在轨运行示意图

1)高温工况：太阳帆处于光照区，薄膜阵面的太阳入射角为0°；

2)低温工况：太阳帆处于地影区，薄膜阵面的太阳入射角为90°。

3.4 太阳帆温度场

基于建立的热分析模型，对太阳帆施加辐射热载荷，包括太阳热辐射、地球热辐射、地球反照辐射、空间环境热辐射，即可得到高温工况和低温工况下薄膜和支撑杆的温度场。

高温工况薄膜温度为-14.75 ℃，豆荚杆的温度范围为-52.4～34.9 ℃；低温工况薄膜温度为-224.42 ℃，豆荚杆的温度范围为-183.0～-186.2 ℃。

豆荚杆截面温度云图如图8所示。可见，高温工况下受太阳照射面和遮挡面存在较大的温度梯度，温差高达87.3 ℃，将引起豆荚杆的弯曲变形。

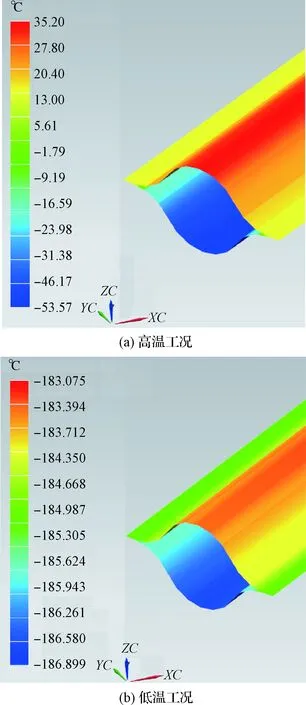
图8 豆荚杆截面温度云图

3.5 太阳帆热变形

建立薄膜和支撑杆的力学分析模型。以20 ℃为参考温度，基于力学分析模型计算薄膜和支撑杆在高温和低温温度场下的热变形。太阳帆由阴影区(低温工况)进入光照区(高温工况)，薄膜的角点面内位移达到42.6 mm，如图9所示。

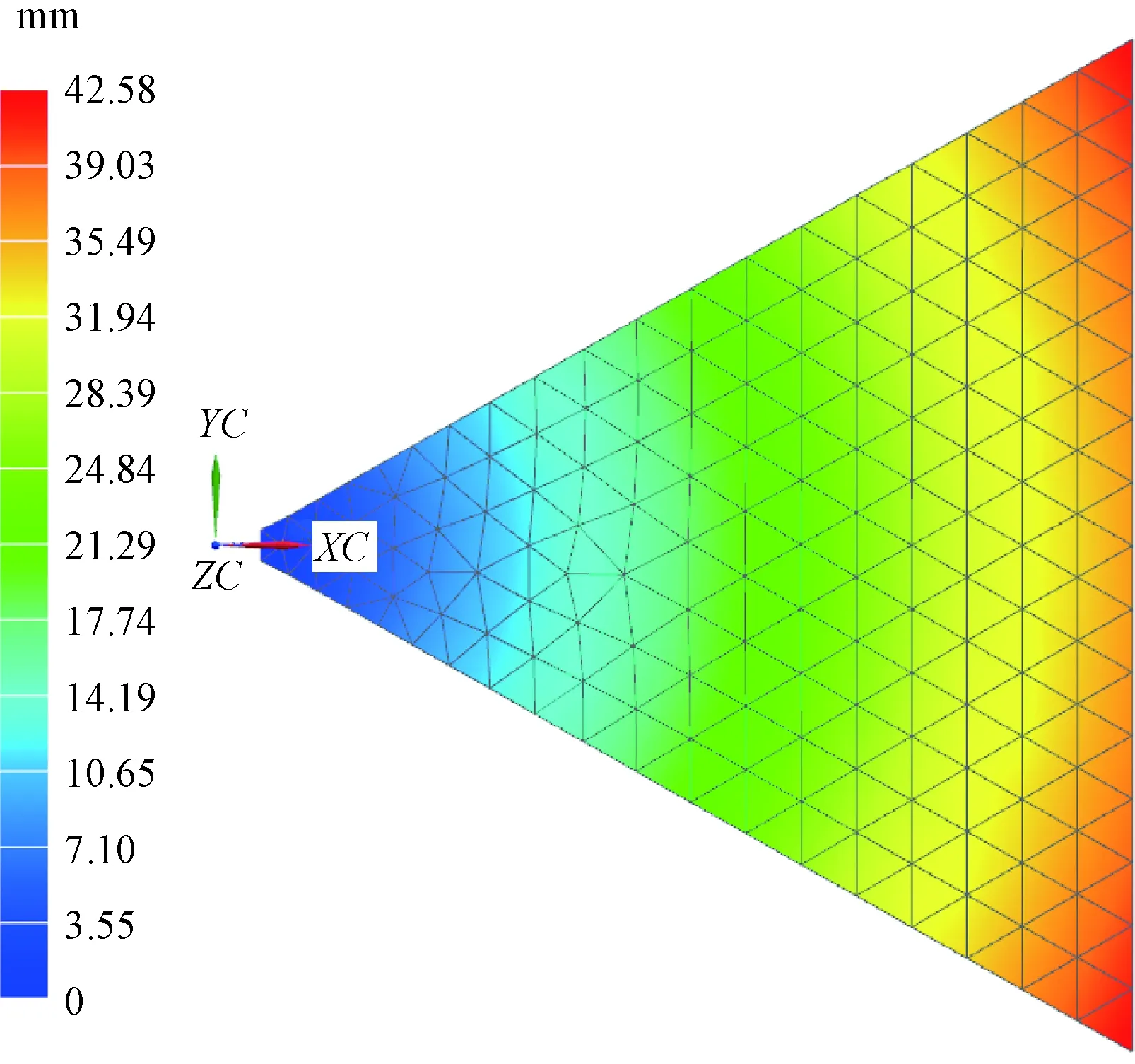
图9 薄膜热致位移(由低温进入高温)

支撑杆热致变形如图10所示。低温工况下支撑杆缩短9.1 mm，顶端横向位移为3.6 mm；高温工况下支撑杆缩短2.8 mm，顶端横向位移为94.3 mm。

图10 豆荚杆伸缩变形

4 形状记忆合金弹簧参数及太阳帆应力

根据高低温下薄膜和支撑杆间的间隙变化情况，确定形状记忆合金弹簧的参数。然后建立含连接单元的太阳帆模型，复核高低温下薄膜的应力。

4.1 形状记忆合金弹簧参数设计

根据薄膜静力分析结果，形状记忆合金弹簧承受的拉力为1 N。弹簧拉力值有两个约束条件：一是保证支撑杆不能产生屈曲，二是保证帆面处于拉紧状态以保持平整。采用欧拉屈曲理论，支撑杆临界屈曲载荷为16.8 N，安全因数设置为3.0，根据稳定性设计准则,单侧弹簧拉力不能超过3.2 N。根据国内外文献调研的结果，在轨时帆面内部应力极小值一般在6.90 kPa附近以使帆面保持平整，由此计算弹簧拉力为1.05 N。为方便计算，本文中弹簧拉力值设为1 N。为使太阳帆在轨运行时，帆面内部应力不发生急剧变化，因此应力极小值变化范围设定为不超过±5%。

图11给出了高低温工况下豆荚杆、薄膜与连接单元相对位置示意图。连接单元在低温工况下连接点为E和J，在高温工况下连接点位F和K。高低温下弹簧行程差=-。根据豆荚杆和薄膜的热变形分析结果，高低温交变时支撑杆变形Δ=6.3 mm，薄膜角点位移Δ=42.6 mm。根据几何关系，弹簧行程近似为36.3 mm。

图11 薄膜张拉点位移示意图

形状记忆合金材料选用钛镍合金，马氏体相变结束温度为29 ℃，奥氏体相变结束温度为55 ℃。合金由高温相奥氏体转变为低温相马氏体后，剪切模量由20.7 GPa减小到2.75 GPa。根据式(1)～(6)确定形状记忆合金弹簧参数，见表2。

表2 形状记忆合金弹簧参数

形状记忆合金表面蒸镀镍涂层，吸收发射比为9.5。根据太阳帆轨道、姿态以及形状记忆合金弹簧参数，建立了形状记忆合金弹簧的热分析模型，计算高低温工况下的弹簧温度。仿真结果表明，低温工况下形状记忆合金弹簧温度为7.5 ℃，高温下为90.9 ℃，满足奥氏体与马氏体之间的相变温度要求。

4.2 太阳帆应力校核

基于有限元软件建立含连接单元的薄膜和支撑杆的力学分析模型，施加温度载荷，可得薄膜在高温工况和低温工况下的应力分布，如图12所示。高温下薄膜应力为6.87 kPa～3.64 MPa，低温下应力为6.54 kPa～3.53 MPa，应力极小值减小了4.8%，满足±5%的约束条件。采用基于形状记忆合金弹簧的连接单元后，温度场变化对薄膜内部应力的影响较小。

图12 SMA弹簧连接的薄膜内部应力云图

将普通弹簧连接作为对照组，设计时为避免高温下发生应力松弛，基于高温工况进行设计。采用普通弹簧连接的薄膜在高温工况和低温工况下的应

力分布如图13所示，由图可见，高温下薄膜内部应力为6.87 kPa～3.64 MPa，低温下应力为55.9 kPa～29.4 MPa，低温下薄膜发生收缩，内部应力增大，弹簧拉力增加到6.78 N，支撑杆安全因数下降为1.43。可见，采用普通弹簧作为连接单元，高温状态下帆面拉紧，当结构进入低温工况时，弹簧拉力急剧增大，支撑杆易发生屈曲。

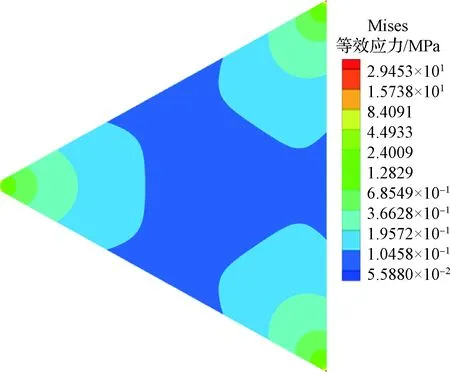
图13 普通弹簧连接的薄膜内部应力云图

5 结 论

本文提出了一种基于形状记忆合金弹簧的太阳帆应力保持方法。在高低温交变环境下，太阳帆航天器的支撑杆和薄膜材料热膨胀系数不一致，从而导致支撑杆与薄膜之间的间隙发生显著变化，温度升高时，间隙减小。同时，形状记忆合金材料在高低温环境下呈现显著的弹性模量非线性特征，形状记忆合金弹簧低温下刚度低、高温下刚度高。因此本文采用形状记忆合金弹簧作为支撑杆与薄膜之间的连接单元，保证了太阳帆在高低温交变环境下薄膜内部应力基本一致。以六边形构型太阳帆为算例进行了仿真，结果表明，采用SMA弹簧后，高温时薄膜应力在6.87 kPa～3.64 MPa的范围内，低温时应力在6.54 kPa～3.53 MPa的范围内，应力极小值变化了4.8%，极大值变化了3.0%，极小值变化满足了变化范围不超过±5%的约束条件。与普通弹簧相比，高低温下薄膜应力状态基本保持一致。本文提出的方法可有效解决高低温交变环境导致薄膜应力发生变化的技术问题，为太阳帆工程设计提供理论参考。