基于机桥耦合振动的滑行道桥优化设计研究

戚春香， 丁丛丛， 李佳坤

(中国民航大学交通科学与工程学院， 天津 300300)

在机场飞行区场道系统组成中，滑行道桥作为其中的主要交通设施，其力学性能表现直接决定了机场运营的效率与安全等级。由于滑行道桥承受的飞机动荷载较大，与常规桥梁的设计有着显著区别，因此其设计经验难以直接应用。研究表明，飞机在滑行道桥上行驶时，机身会与滑行道桥产生耦合振动，这会直接影响到桥梁寿命和飞机安全性。严志刚等[1]通过建立桥面平整度沿纵向分布函数，提出一种考虑桥面平整度对振动影响的简化计算模型；张艳鹏[2]结合广州白云机场的滑行道桥，通过模型校正的梁格法研究了飞机-滑行道桥耦合振动响应；孙荣梅[3]利用模态叠加法研究了飞机二自由度模型下飞机-滑行道桥耦合振动响应；张宇辉等[4]借助有限元手段对滑行道桥进行实体仿真建模研究，模拟其在不同荷载和振动情况下的力学性能及形变，对地震波作用进行了预测分析。这些研究成果为现阶段滑行道桥的安全评估与检测提供了评估指标与理论依据。

研究表明，在影响机桥耦合振动的若干因素中，滑行道桥结构参数尤为显著，而现阶段关于滑行道桥振动响应的研究尚且不够成熟，大多借鉴于公路、铁路系统的研究成果。Xiang等[5]提出了一种通用三维虚拟测试元件(3D virtual testbed, 3D VTB)，借助制定的3D VTB元素矩阵，获得评估车桥动态响应以及行驶列车稳定性和安全性的指标；黄维蓉等[6]结合室内试验, 研究车桥耦合振动下混凝土性能变化规律, 为实现不断交情况下桥梁的维修加固提供了理论依据。Duan等[7]分析了列车-桥梁耦合效应系统，提出用于评估桥梁阻尼振动的向量式有限元素法(vector form intrinsic finite element, VFIFE)；尹钱求[8]分析了桥墩截面形式与质量、材料强度等设计参数对桥梁结构在水平方向振动性能的影响，得出圆端形截面桥墩、较大桥墩重量有利于改善桥墩的横向振动性能；张昀青[9]以钢轨竖向振动位移解为基础，得到结构参数变化对列车动载及轨枕力学响应的影响规律；罗锟等[10]基于车桥耦合动力学分析模型，借助有限元法得出时间和频率两个领域角度的高架轨道箱梁结构的振动特性规律。蒋培文[11]基于4座大跨连续体系桥梁的结构尺寸，模拟了不同跨径与墩高的连续体系桥梁的正交试验，得出桥梁总跨数、墩高、中跨跨径以及桥面平整度等级等影响因素对桥梁各项动态响应参数的影响规律。由于滑行道桥桥面宽、刚度大、承受飞机主起落架位置的荷载大而集中，与公路与铁路桥梁的结构形式具有显著区别，车桥耦合振动领域的研究模型与评价指标对于机桥耦合振动来说无法完全适用。因此，开展关于滑行道桥结构参数对机桥耦合振动影响的研究具备重要的理论意义与工程应用价值。

现针对滑行道桥的结构形式，采用理论和数值模拟的方法研究滑行道桥结构参数中的梁截面形式、桥梁跨度、连续梁跨数及边跨比对机桥耦合振动响应的影响，提出了滑行道桥在常见机型作用下的合理跨度范围及结构形式，为滑行道桥的结构设计与健康诊断提供了新的方法与思路。

1 飞机-滑行道桥耦合振动方程

1.1 简支梁桥振动方程

桥梁的整体结构布局形式、构件几何尺寸、材料基本特性等因素直接决定了桥梁结构的刚度和质量。参考张钧博[12]以欧拉-伯努利梁为研究对象，得到的简支梁桥的全桥自由振动方程，可表示为

(1)

T(t)=Asin(ωt+φ)

(2)

(3)

式中：y1(x,t)为简支梁桥竖向挠度曲线；x为简支梁桥上一点沿桥长方向至起始端的距离；i为简支梁桥振型阶数；Xi(x)为简支梁桥无约束振动下的振型函数；Ti(t)为时间参数影响下的模态坐标；t为飞机滑行时间；A和φ为桥梁初始振动常数；ω为梁自由振动圆频率；C0为任意常数；L1为简支梁桥长度。

1.2 连续梁桥振动方程

采用杠杆法求解连续梁的支座反力。杠杆法是以某一荷载作用跨作为基本静定结构，撤去其余全部支座，撤去的支座以单位荷载作用在基本结构上构成解算体系，最终得出各支座反力，将得到的支座反力作用于整个桥梁，即在形式上将连续梁转化为简支梁计算[13-14]。

如图1所示，以三跨连续梁为例，连续梁支座从左向右依次为A、B、C、D，跨径分别为L12、L23、L34，竖向集中荷载P作用于E点，与A支座之间的距离为x。

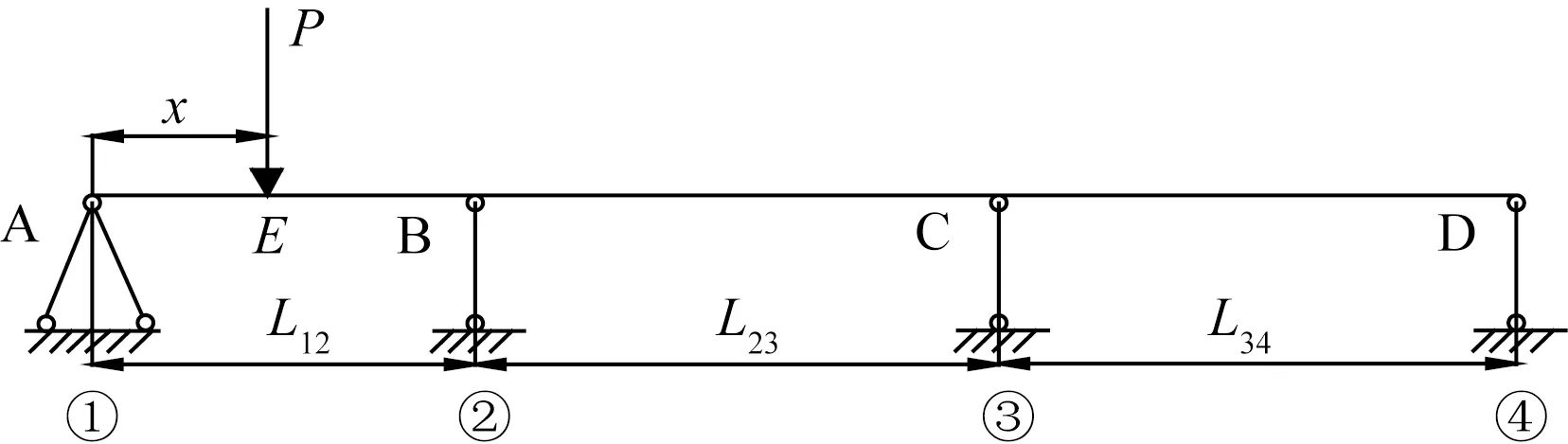
图1 三跨连续梁荷载作用示意图

如图2所示，采用杠杆法进行求解时，先将多跨连续梁的各支座按从左向右顺序编号，即①、②、③、④，然后撤去荷载P作用的AB跨以外的全部支座约束，分别用X3=1、X4=1代替，进而形成解算的基本体系，以求解各支座反力。

图2 杠杆法基本体系图

以三跨连续梁桥为例，参考车桥耦合模型计算方法，采用移动恒力过桥方式求解，其微分平衡方程为

(4)

式(4)中：E为连续梁桥的弹性模量，I为连续梁桥的截面惯性矩，EI即为连续梁桥的抗弯刚度；m为连续梁桥的质量；t为移动恒力通过连续梁桥的时间；δ为狄拉克函数；f1和f2为中间两个支座的反力；a1和b1为中间支座到桥端的距离。

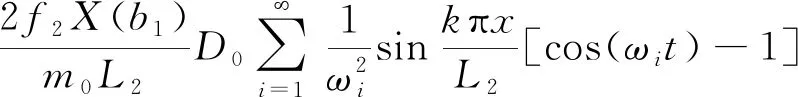
(5)

式(5)中：k为任意整数；ωi为连续梁桥的自由振动圆频率；y2(x,t)为连续梁桥竖向挠度曲线；X(·)为连续梁桥无约束振动下的振型函数；D0为任意常数；L2为连续梁桥长度。

为验证上述方法得到桥梁振动方程的正确性，以矩形截面、跨度为20 m、梁高为0.6 m、梁宽为0.3 m的三跨连续梁为例，对式(5)进行二次求导和傅里叶变换，得到滑行道桥的基频为8.23 Hz。同时采用ANSYS建模并进行模态分析，得到该三跨连续梁基频为8.47 Hz，误差为2.8%，因此可认为所得梁桥的振动方程是正确的。

1.3 飞机振动方程

参考文献[15]，建立飞机模型，由于飞机在低速滑行过程中，其左右摆动对滑行道桥的竖向振动影响很小，故将飞机简化为四自由度模型，分别为前、后起落架的竖向运动、机身的竖向运动和纵向俯仰运动，其简化模型如图3所示。

图3 飞机简化模型

飞机模型的假定：①飞机沿纵向对称；②飞机主起落架整合为一个当量起落架；③起落架缓冲系统的弹簧刚度系数为线性，取力-位移曲线上对应停机状态点的斜率。

飞机系统的振动平衡微分方程为

(6)

式(6)中：h1、h2分别为前、主轮的桥面输入；以飞机重心处为坐标原点构建直角坐标系，横轴x沿水平方向向左，纵轴y沿垂直方向向上，飞机滑行速度为v；m为机身质量；m1、m2为前、后起落架非弹性支撑质量；I为飞机绕重心的惯性矩；l为前、后起落架间距；a为前起落架与重心间距；b为后起落架与重心间距；K1、K2为前、后起落架与机体间弹簧刚度系数；K3、K4为前、后起落架轮胎弹簧刚度系数；C1、C2为前、后起落架油液阻尼系数；Z1、Z2、Z分别为前、后起落架、飞机重心处的竖向位移；θ为重心处的俯仰角。

将式(6)写成矩阵形式，可表示为

(7)

式(7)中：

(8)

R=(K1h1,K2h2,0,0)T

(9)

Z=(Z1,Z2,Z,θ)T

(10)

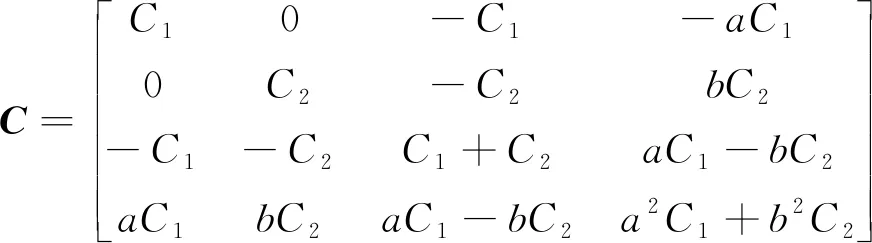
(11)

1.4 飞机-滑行道桥耦合振动方程

建立飞机-滑行道桥耦合振动方程，可采取将飞机和滑行道桥通过接触点的位移联立的方法，由于飞机与滑行道桥系统的复杂性，对其进行机桥耦合振动分析时，需要做出以下的假设：①飞机在匀速滑行过程中，轮胎始终与桥面保持紧密接触；②飞机沿纵向对称，桥面不平整度沿横向分布不变；③飞机与滑行道桥的接触属于点接触。

(12)

式(12)中：F1和F2分别为飞机的前、后起落架作用在滑行道桥的力；l为前、后起落架间距；m2为飞机主体质量；E为弹性模量；I为截面惯性矩；y为滑行道桥的竖向位移；x为飞机沿桥面的滑行距离；v为飞机滑行速度。

2 有限元模型

在进行滑行道桥耦合振动分析时，考虑桥面平整度带来的影响[3]，采用梁格法建立钢筋混凝土滑行道桥模型。桥面不平整度模型为

(13)

表1为各等级桥面的不平整度系数。

表1 不平整度系数

2.1 梁格法建模

[3]

每段纵梁的计算刚度为

(14)

式(14)中：Dx、Dy为梁格构件沿x和y方向的抗弯刚度系数；Dτ为梁格构件的抗剪刚度系数；Dxy为梁格构件的抗扭刚度系数；μ为混凝土材料的泊松比；Ix、Iy分别为横梁关于x、y方向的截面惯性矩；Jx、Jy分别为纵梁腹板关于x、y方向的截面扭惯性矩；a2、b2为腹板距离。

在建立滑行道桥及飞机的仿真模型中，所需的设计参数如表2、表3所示。

表2 滑行道桥材料参数

图4 梁格法滑行道桥有限元模型

表3 飞机参数

2.2 飞机等效荷载

对于连续梁、简支梁的模拟计算分析，采用等效荷载法。选取飞机模型为四自由度、移动荷载模型，利用该模型模拟飞机在不同桥梁上的滑行，忽略各自由度的阻尼力、弹簧力和惯性力，研究飞机速度、位移和加速度与桥梁各参数的关系，利用MATLAB软件中CFTOOL功能将其拟合为一个周期性函数。邓爱民等[16]研究指出，周期函数主要与幅值和周期有关，周期取决于飞机滑行速度和桥梁长度，幅值的确定可采用模拟计算法。借助上述飞机荷载模型得到滑行道桥的振动响应，提取质点处时程曲线的极值可确定各参数的幅值，继而得到等效荷载拟合函数，具体公式如下。

(1)位移。

(15)

(2)速度。

v=v0sin(2πv/l0t)

(16)

(3)加速度。

a=a0sin(2πv/l0t)+b0sin(πv/l0t)

(17)

式中：f0为飞机初始位移；A为时程曲线的振幅；ω0、ω为时程曲线的振动频率；tc为飞机滑行至桥面跨中处所需的时间；v0为飞机初始滑行速度；l0为飞机滑行距离；a0、b0为常数。

3 滑行道桥结构参数对耦合振动影响

3.1 桥梁截面形式

在桥梁结构中，桥梁截面具有诸多形态，截面形式的区别使得结构产生的振动响应也各不相同。选取箱型与T型的滑行道桥截面，两种截面尺寸如图5、图6所示。

图5 箱型截面局部尺寸

图6 T型截面局部尺寸

参考某机场现役箱型截面滑行道桥尺寸以及邵旭东[17]建议的桥梁高跨比范围，分别建立箱型截面与T型截面两种形式的滑行道桥模型，桥宽为50 m，跨度分别为14、16、18、20、22、24 m，分析飞机以相同速度滑行经过滑行道桥的跨中最大挠度。令aratio为箱型截面跨中最大挠度与T型截面跨中最大挠度的比值，图7给出了参数aratio随滑行道桥跨度的变化规律。

由图7可见，在激振荷载作用下，相同跨度的箱型截面滑行道桥跨中挠度小于T型截面桥梁。随跨度的增加，aratio值逐渐减小。说明桥梁跨度越大，两种截面桥梁的跨中挠度差异越大，即箱型梁的耦合振动响应越优于T型梁。

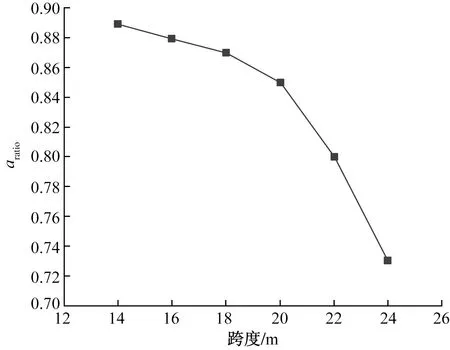
图7 参数aratio随跨度变化曲线

进一步，通过滑行道桥的模态分析，可以得到不同跨度下箱型简支梁与T型简支梁基频的变化情况，如图8所示。

由图8可知，桥梁基频随着跨度的增加逐渐减小，相同跨度的箱型截面桥梁基频高于T型截面桥梁，随着跨度的减小，截面形式的改变对基频的影响减小。

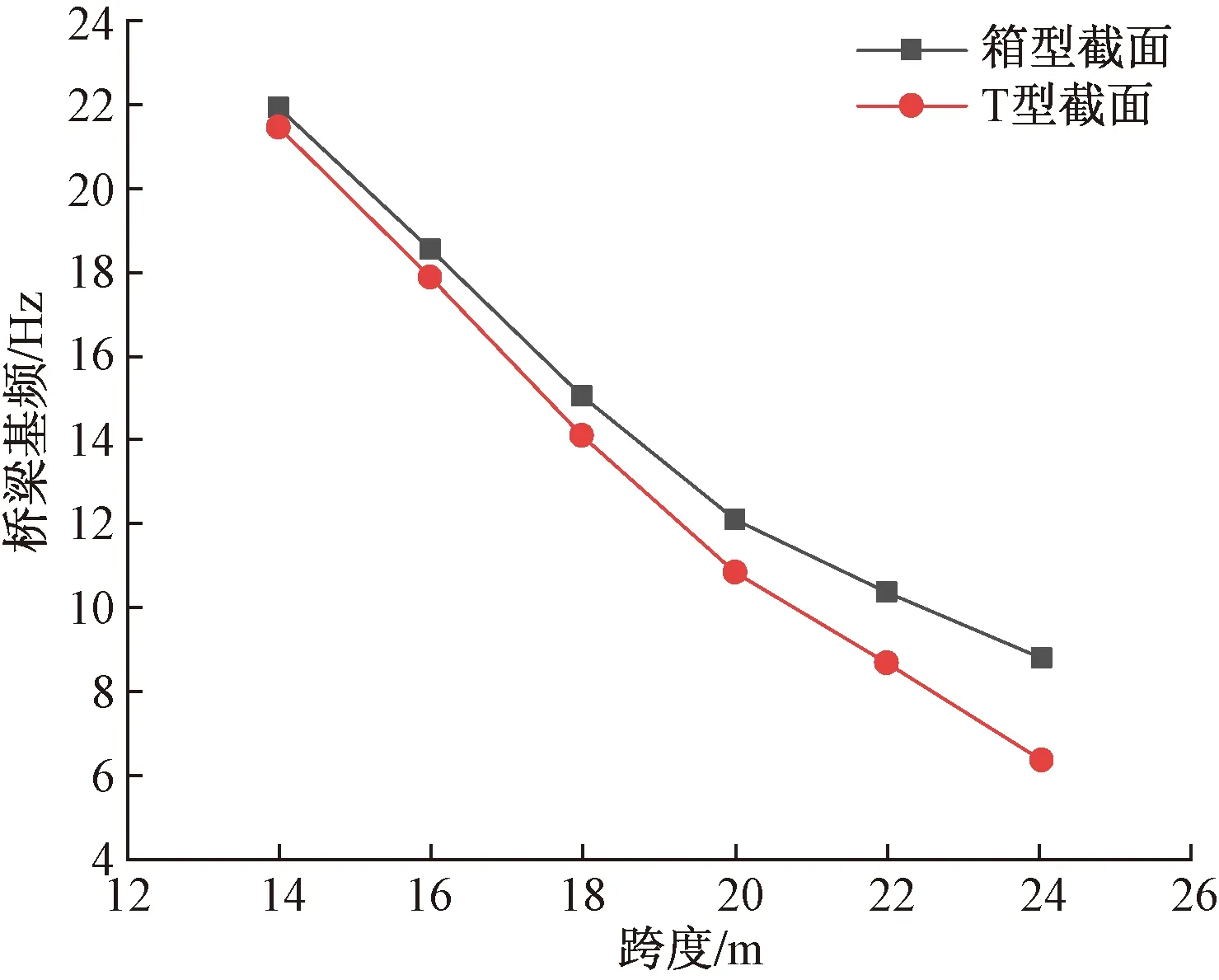
图8 简支梁基频变化曲线

3.2 滑行道桥跨度

为了分析跨度对机桥耦合振动响应的影响，选取跨度分别为14、16、20、22、24 m箱型截面的滑行道桥模型进行分析，提取各跨度下的跨中最大挠度，其变化规律如图9所示。

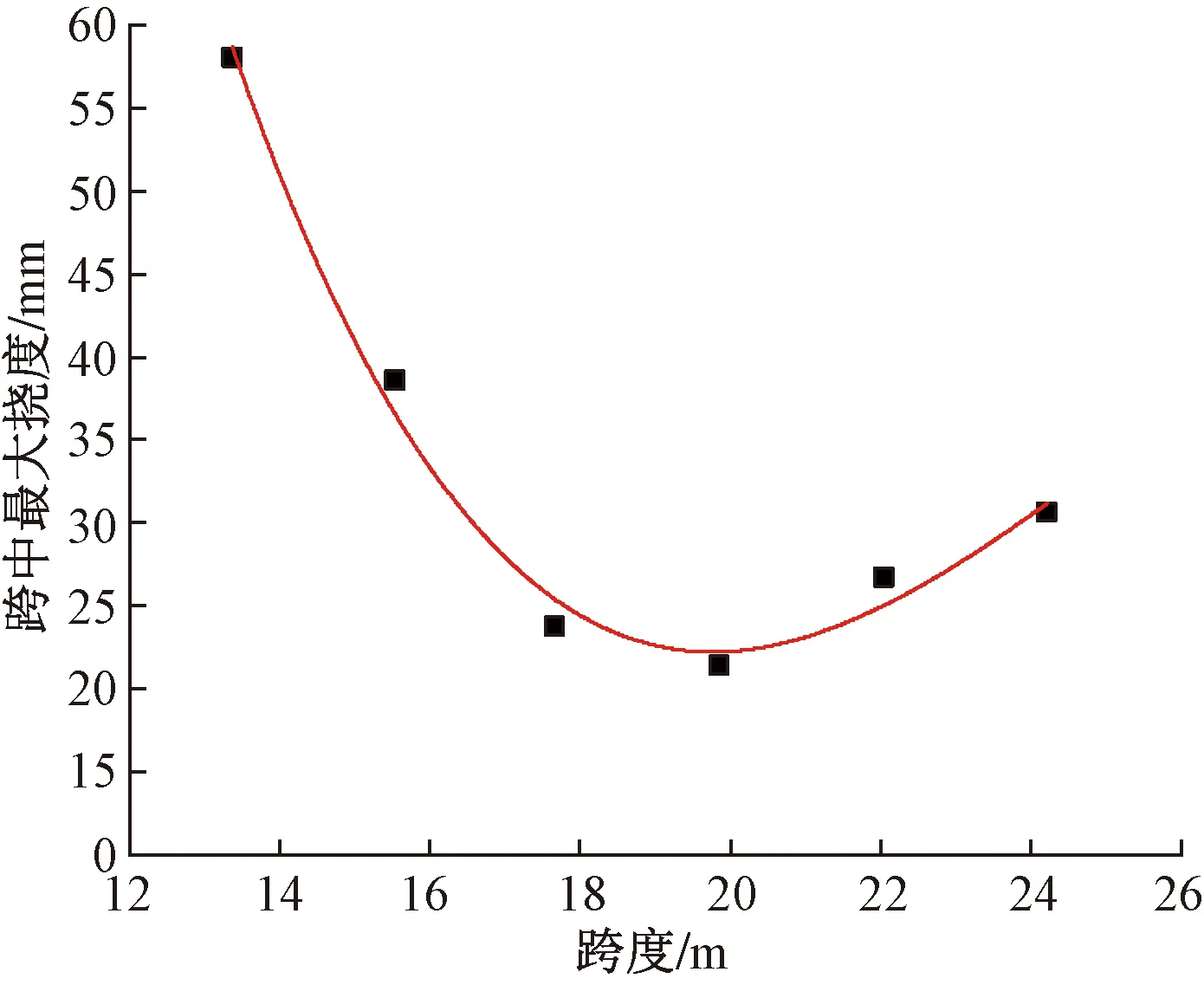
图9 不同跨度简支梁跨中最大挠度变化曲线

由图9可见，随着跨度的增加，跨中最大挠度呈现先减小后增大的趋势。对应图8可知，跨度在14～15 m时桥梁的基频较大，此时滑行道桥基频和飞机频率较为接近，跨中位移响应也最大；当跨度大于15 m时，滑行道桥基频和飞机频率逐渐远离，跨中最大挠度呈下降趋势，频率对挠度的影响逐渐减小；当跨度达到20 m时，跨中最大挠度再次增加。由此可见，对于A320飞机，滑行道桥跨度在17～20 m 范围时，其跨中振动响应较优。

3.3 连续梁跨数影响对比分析

分别建立单跨简支梁、两跨至五跨连续梁滑行道桥模型，梁的跨度分别为18、20、22 m，分析飞机荷载作用下，滑行道桥的振动响应。图10给出了3种不同跨度滑行道桥跨中最大挠度随跨数变化规律。

图10 不同跨度连续梁桥跨中最大挠度变化曲线

由图10可见，相同跨数条件下，滑性道桥跨度越大，跨中最大挠度也越大。3种跨度下的滑行道桥，随着跨数的增加，其跨中最大挠度均随之逐渐减小，当跨数达到四、五跨后趋于稳定。可见，对于20 m左右跨度的连续梁桥，三跨以上的跨数结构响应较小。

3.4 连续梁边跨比影响对比分析

连续梁的设计要考虑到边跨比这一因素，合理的边跨比可以降低连续桥梁的响应，使得各跨的响应接近相同，从而同时达到设计寿命。

取三跨连续梁，跨中跨度为20 m，边跨比分别为0.9、1.0、1.1，选取第一跨进行分析，计算得其跨中位移时程曲线如图11所示。

图11 不同边跨比下跨中位移时程曲线

由图11可见，边跨比从0.9增加到1.1时，第一跨的跨中最大挠度随之增加。因此，若想均衡每跨的最大挠度值，需要选取合适的边跨比。取中跨跨度为20 m的四跨连续梁，桥梁边跨比分别为0.95和1.0，分别计算其跨中位移时程曲线。如图12所示。

图12 不同边跨比跨中位移时程曲线

由图12可以看出，对于四跨连续梁，当边跨比为0.95时，第一跨的跨中最大挠度与中跨接近，说明其最优边跨比为0.95。

对于五跨连续梁，选取桥梁边跨比为1.0和0.94，分别计算两种情况下的跨中位移时程曲线，如图13所示。

图13 跨中位移时程曲线

图13(a)中，3个曲线的最小值分别为6.86、5.29、5.10 mm；第二跨和第三跨的最大挠度基本相同，约为边跨的78%，如图13(b)所示，边跨比为0.94时，三跨的跨中最大挠度基本一致，说明对于五跨连续梁的滑行道桥，其最优边跨比为0.94。

4 结论

(1)不同截面形式下，箱型梁的跨中最大挠度要明显小于T型梁，且箱型梁的基频均高于T型梁。

(2)简支梁的基频会随着跨度的减少而增加，合理的简支梁跨度可以有效降低桥梁的振动响应，对于A320飞机，跨度在17～22 m范围的简支梁桥振动响应最小。

(3)连续梁的跨数和边跨比对机桥耦合振动影响规律表明：随着跨数的增加，滑行道桥跨中最大挠度逐渐下降趋于平缓，对于跨度20 m左右的连续梁滑行道桥，四、五跨数是较优的桥梁形式；对于四、五跨连续梁，其最优边跨比分别为0.95和0.94。