步态信号采集与分类平台的设计与实现

陈东毅，李玉榕

(1.福州大学 电气工程与自动化学院，福建 福州 350108；2.福建省医疗器械和医药技术重点实验室，福建 福州 350108)

人在指定的红外、激光探测区域行走时会产生幅值持续变化的电信号，将该信号经过软硬件处理后可以用于表征人的步态特征信号，该特征信号直观反应了人的行走状态与健康状况[1]。特别是在足下垂患者的临床康复中，步态的检测、分析对揭示患者异常步态的成因、制定康复训练计划与后期的康复状态评估起到了至关重要的作用[2-5]。

目前，主要的步态评估方法有主观观察法和量表评分法，部分研究机构会利用三维运动捕捉系统和测力平台进行评估。主观观察法带有明显的个人主观差异，步态评估的可靠性不足；量表评分法提供的步态信息不够客观、准确；三维运动捕捉系统和测力平台与之相比虽具有较好的准确性和可靠性，但昂贵的价格、高门槛的技术要求和场地的限制等因素导致了其无法在临床诊断中得到大规模的使用[6-9]。鉴于此，如何在实时变化的步态信号中准确并快速地表征不正常的步态信息是步态评估的关键所在，搭建低成本、易实施、无接触式的步态信号采集与分类平台是将步态评估方法进行实际临床应用的重要举措。

为了解决上述的问题，本文提出了改进经验模态分解(empirical mode decomposition, EMD)结合Bagging正则化共空间模式(Bagging regularized common spatial pattern, BRCSP)与Fisher线性判别分析法(Fisher linear discriminant analysis, FLDA)的步态识别新方法，并设计了一套基于红外、激光等探测器的步态检测与分类实验平台。通过理论论证和实验验证表明，该平台实现了步态自动识别的功能；能准确表征异常步态信息，为步态的健康评估提供科学依据。

1 改进的步态信号经验模态分解

非线性、非平稳的步态信号经过传统EMD后，会得到含有低频虚假的、有限阶次的本征模态分量(intrinsic mode function, IMF)。为了得到既包含步态特征信息又无高频干扰噪声的步态信号，文献[1]和[10]提出了改进的EMD算法，克服了传统EMD分解对低频段步态信号特征分析的影响，从而获得准确的步态信号。

1.1 能量矩占比

计算各阶IMF能量与步态信号总能量的占比，对比后筛选出占比大的IMF分量，滤除虚假的IMF分量[1,10]。

各阶IMF能量Ei及其与步态信号总能量的占比T，计算如下：

(1)

(2)

式中：n为总的采样点数；k为某采样点；Δt为采样周期；ci为第i个IMF分量。

1.2 方差贡献率

引入方差贡献率Mi来突出各阶IMF分量的相对重要程度，计算公式为

(3)

其中：

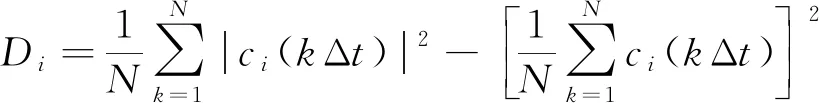
式中：Di为第i个IMF分量的方差；n为总的采样点数。由式(3)可知，若某阶IMF分量在原信号中越重要，则其Mi值就越大[1,10]。

1.3 步态信号分解与重构

非线性、非平稳的步态信号x(t)被分解为有限阶次的、含有时间尺度信息的一系列IMF分量ci(t)和残差rn(t)，表示为

(4)

式(4)选取出有用的IMF分量，经过线性插值法后得到步态的重构信号[1,10]。

2 Bagging正则化共空间模式算法

共空间模式(common spatial pattern, CSP)是一种适用于二分类判别的空间滤波器，通过构造最优空间滤波器，使多通道的步态信号矩阵的方差值差异最大化，得到具有明显区分度的特征向量[11-12]。正则化空间模式(regularized common spatial pattern, RCSP)算法优化了CSP算法对噪声敏感的问题，但该算法的稳定性与分类准确度有待提高[13-14]。

本文将提前采集到的步态数据作为步态训练样本数据包，利用Bagging思想即通过重复选取训练样本数据包的方法，将训练的样本数据以数据包的形式进行划分。Bagging正则化共空间模式(Bagging regularized common spatial pattern, BRCSP)算法继承了RCSP中关于迁移学习的算法理念，将其他被试者的步态数据加入到RCSP的算法中，计算被试者信号的协方差矩阵，最后求出具有显著特征的特征分量；该算法的优势在于强化了步态信号的个体差异性，保留共有特征及提高算法的准确度[15]。

2.1 被试者步态信号的协方差矩阵

根据被试者的步态信号建立协方差矩阵，假设矩阵Dnor和Dabnor分别表示经过改进EMD后的步态信号矩阵(下标nor和abnor分别表示正常步态和非正常步态)，为N×M维，通道数用N表示，M为每个通道的采样点数，trace()表示矩阵的迹。标准化后的空间协方差为Cnor、Cabnor，表示如下：

(5)

(6)

2.2 基于BRCSP的协方差矩阵估计

通过RCSP计算各类正则化空间协方差矩阵，计算公式为

(7)

式中：β和γ是两个正则化参数(0≤β,γ≤1)，β为训练样本协方差矩阵的权重值，用来减少协方差矩阵估计的偏差，γ为多个单位矩阵的权重；Xi(β)为特定被试者及其他被试者的步态数据的协方差矩阵，下标i取值为1、2，分别表示正常步态和非正常步态；I为N×N单位矩阵。

其中：

(8)

式中：Ci为被试者第i类的M个训练数据组成的协方差矩阵；Ci′为其他被试者第i类的M′个训练数据组成的协方差矩阵，引入该项的作用是通过减少协方差矩阵估计的方差得到更可靠的分类结果。

对协方差矩阵，式(5)—(8)对角化分解，可得

(9)

由奇异值分解定理可知，对复合协方差矩阵S进行正定矩阵的特征分解，可以得到特征值按降序排列的白化矩阵

对平均协方差矩阵进行变形：

(10)

(11)

其中，Qnor、Qabnor具有公共特征向量，同时存在两个对角阵Λnor、Λabnor以及相同的特征向量矩阵B，对式(10)和(11)进行主分量分解，得到式(12)—(14)如下：

Qnor=BΛnorBT

(12)

Qabnor=BΛabnorBT

(13)

Λnor+Λabnor=I

(14)

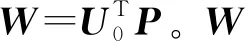
Z0=D(t)·W

(15)

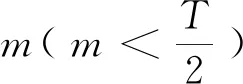
f=[f1,f2,…,f2m]T∈R2m×1

(16)

其中：

最后，再使用FLDA将特征向量映射到低维度的空间中，实现对步态信号的准确分类。

3 步态信号的Fisher分类判别

FLDA的主要思想是以降维的方法求取最佳投影轴，使得类间间距最大化、类内间距最小化，将两类信号显著区分开[16-18]。

由式(16)得到特征向量f，求出两类数据特征向量的均值mj，如式(17)所示。下标j取值为1、2，分别表示正常和非正常步态。类内距离Sw是两类数据的方差和，如式(18)所示。

(17)

(18)

式中：Nj为不同类特征向量fpj的数据点数，其中X∈fpj。

求出类间距离Sb，用式(19)表示：

Sb=(m1-m2)(m1-m2)T

(19)

求出投影矩阵A*，用式(20)表示：

(20)

最后，将步态数据向法向量A*进行投影，得到Y=(A*)TX。

4 步态信号的分类过程

步态信号的分类过程如图1所示。将步态信号进行改进EMD滤波，分解得到有效IMF分量进行信号重构，对去噪后的步态信号利用BRCSP进行特征提取，最后利用FLDA对步态进行特征分类。

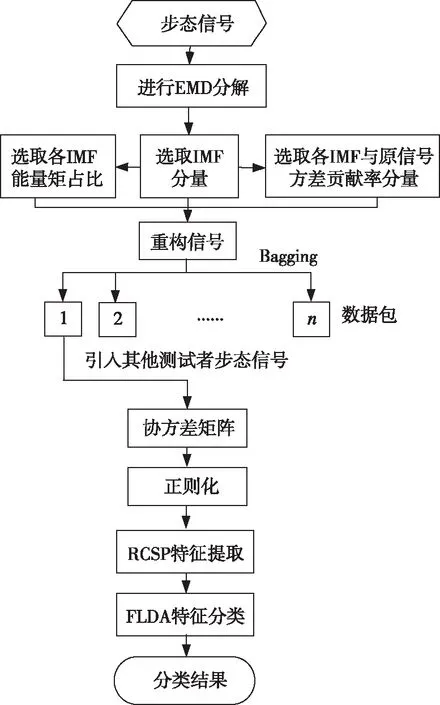
图1 步态信号的分类过程Fig.1 Gait signal classification process

5 步态信号检测与分类平台的设计

5.1 平台的硬件设计

基于红外、激光探测器等搭建了步态信号检测与分类平台。该平台主要由前端探测器模块、电平转换电路、信号调理电路、电源供电电路、STM32控制器，以及步态信号特征提取模块、步态信号特征分类模块、分类结果液晶显示模块等组成；其中前端探测器模块由红外探测器、激光测距传感器、红外光栅阵列等组成。平台的硬件结构设计和电路实物图如图2、3所示。

该平台搭配选用多种传感器模块，通过搭建电平转换电路与信号调理电路实现步态信号的预处理。STM32控制器主要负责步态信号特征提取与分类的算法运行，通过串口通信将步态信号与分类结果显示到液晶屏上，实现对进入检测区域的步态信号自动检测与分类的功能。

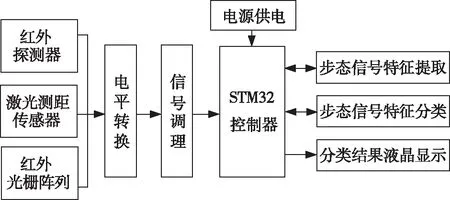
图2 步态特征分类实验平台硬件结构设计Fig.2 Design of hardware structure of gait feature classification experimental platform

图3 平台电路实物图Fig.3 Physical diagram of platform circuit

5.2 平台的软件流程设计

本文设计的步态信号检测与分类平台的软件运行流程，如图4所示。软件开始运行时，前端各传感器工作在正常状态下，主程序静默等待步态信号的触发，之后对触发的信号进行特征提取，判定是否为步态信号，再对步态进行分类，最后将步态信号、分类结果一同显示到LCD液晶屏。

6 结果分析

6.1 步态信号采集

在指定的探测区域内有步态信号产生，前端探测器采集到幅值连续变化的电信号经过电平转化、信号调理等处理后的正常、非正常步态信号，如图5所示。

图4 步态信号实验平台软件运行流程Fig.4 Software running process of gait signal experiment platform

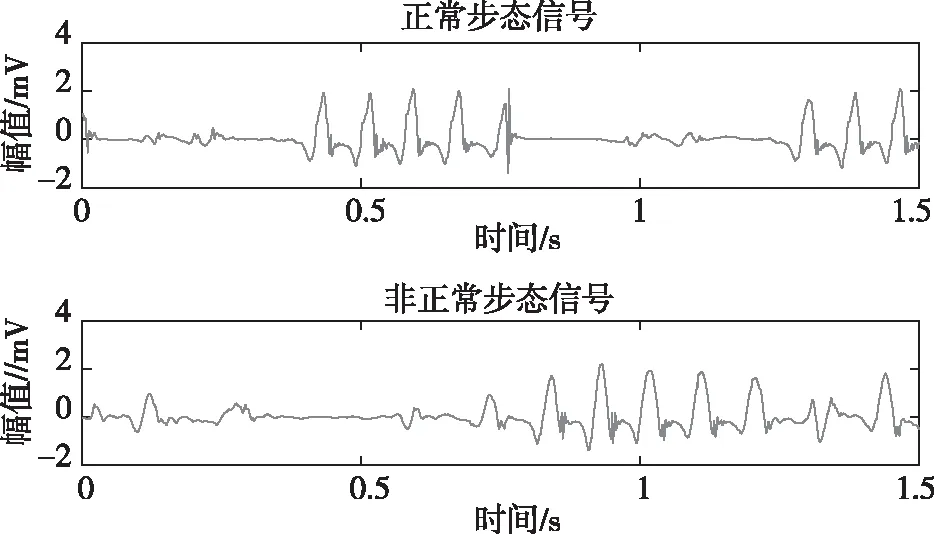
图5 步态信号波形图Fig.5 Gait signal waveform diagram

6.2 步态信号的特征提取与分类

经过EMD后的步态信号各阶IMF分量能量矩占比T、方差贡献率M分别由式(2)、(3)给出，表1给出了步态信号的特征参数。

表1 步态信号特征参数 单位：%

对前5阶IMF分量运用线性插值法进行信号重构，重构后的步态信号经过BRCSP、FLDA后的特征分类，如图6所示。

图6 步态信号特征值分布图Fig.6 Characteristic value distribution diagram of gait signal

由图6可知：经过改进EMD滤波和BRCSP特征提取等处理后的步态信号，在FLDA上可以找到最佳投影轴实现正常与非正常步态的准确分类，分类结果之间具有明显的类间间距和类内间距，使得步态的个性差异化和共有特征得到完整体现。为了进一步提高步态分类的精度，通过建立大量的正常、非正常步态数据集来强化不同步态之间的特征值。

6.3 实验结果

利用步态信号实验平台对不同测试者在不同的步行速度下进行步态二分类实验，结果见表2。测试者1～3模拟足下垂患者的步态，测试者4～5模拟正常人的步态；测试者以0.15、0.20、0.25、0.30、0.35 m/s的步速通过同一个红外、激光探测区，步速分别以v1、v2、v3、v4、v5表示。实验结果表明该平台对步态能做出准确的分类。

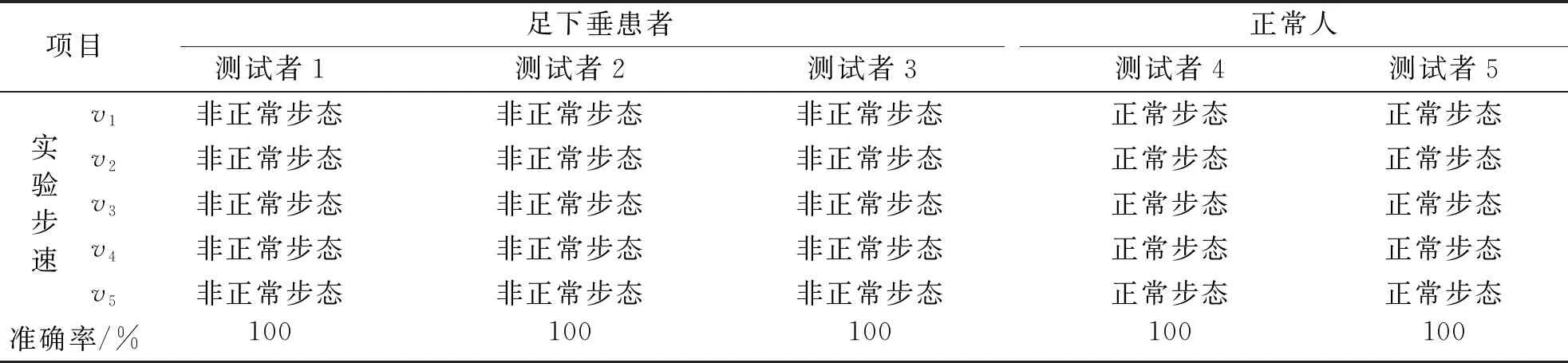
表2 不同步态二分类实验结果Tab.2 Experimental results of binary classification of different gaits

为了充分验证新方法的有效性和可行性，利用本文设计的硬件平台进行大量的步态信号采集实验，然后利用支持向量机(support vector machines, SVM)、BP神经网络、RBF神经网络、CNN卷积神经网络进行步态二分类识别的对比实验。其中，支持向量机中最优参数惩罚因子c与基于高斯径向基RBF的核函数参数g是通过网格法进行全局搜索并寻优后得到的；BP神经网络隐含层神经元个数为12，输入层与隐含层之间是tansing函数，隐含层与输出层之间是purelin函数，迭代次数为100，训练的误差目标设置为0.000 01；RBF神经网络的最大神经元个数为3 000，训练的误差目标设置为0.000 01；CNN卷积神经网络由8层网络组成，输入层为32×16的数据量，卷积层有2个特征图，卷积核大小为5×5[19]。测试者仍以0.15、0.20、0.25、0.30、0.35 m/s的步速经过探测区域，步速分别以v1、v2、v3、v4、v5表示，每种步速进行30次实验。对经过5种不同算法计算后得到的步态分类准确率进行对比，结果见表3。

表3 不同分类方法的步态分类准确率对比 单位：%

由表3可以看出，本文算法较其他算法具有更高的分类精度，表明该算法对步态特征提取是准确有效的。对算法的耗时进行比较发现，本文算法基于矩阵的运算，不涉及模型、网络的建立，算法矩阵的计算量很小；但前4种算法需要进行网络的优化和参数的迭代，耗时长、计算量大，说明复杂的智能化算法对系统的耗时影响显著，不利于软件算法的实现，会导致平台总体造价的提高。综上所述，本文提出的算法相较于其他算法，在分类准确率、识别快速性及算法实现方面等问题上具有一定的优势。

7 结论

本文应用改进EMD，结合BRCSP与FLDA判别法，设计了一个能够准确识别步态信号的平台，实验结果表明该平台对步态信号的平均识别准确率达到96.6%。相比现有的步态评估系统，该平台的优势表现在：步态信号的共有特征及个体步态的差异性得到有效的强化；平台的硬件组成结构简单、模块化设计，软件算法易于实现，总体造价低廉；不受测试环境、空间条件的约束，平台易于在有限的空间内进行部署并实现步态的快速检测与分类；无接触式的步态检测极大地降低了对被试者的外部干扰，免除了穿戴式传感器等检测装置需要保证牢固穿戴、设备重复标定的困扰。

下一步的工作方向是进一步改进算法，通过建立大量的步态数据样本集来强化正常、非正常步态的特征值，进一步提高步态分类的精度，同时细化非正常步态的分类结果，实现对非正常步态不同严重程度的评估，预测人体的康复状态及健康趋势。