模糊自抗扰的双电机同步驱动电动缸起竖策略*
2022-07-11陈俊侨汪晓军崔臣君王海岳
陈俊侨,汪晓军,崔臣君,王海岳
(1.中国航天科工二院研究生院,北京 100854;2.北京机械设备研究所,北京 100854)
0 引言
双电机同步驱动系统相对于单电机驱动系统,体积、质量更小,动力分散,同时满足输出功率的要求。双电机驱动克服了传动距离小、结构布局限制等单电机驱动存在的缺点。实现双电机同步方式多为耦合式控制,能够减小同步所需时间、提高同步精度[1-2]。
对于双电机同步驱动电动缸起竖系统,在起竖过程中,负载扰动随角度而呈非线性变化;此外也存在摩擦等其他非线性因素。为了提高系统的稳定性和鲁棒性,国内外学者提出不同应用于伺服系统中的控制方法。模糊PID 控制能够通过输入信号及其微分信号,实现参数自整定,然而PI 控制器存在带宽有限、抗扰动能力弱等缺点[3-5];RBF(radial basis function)神经网络控制算法相比传统PID 算法,提高了精确度,但其运算量过大导致其很难在短时间做出灵敏的反应,且容易陷入局部最优而无法取到全局最优[6-9];自抗扰控制对于负载扰动具有较强的鲁棒性,且其建模不依赖系统模型。但是由于参数整定之后,不能在线实时调整,控制器无法同时兼顾起竖系统的快速性和抗干扰能力,将会使起竖过程负载扰动变化影响双电机同步性[10-11]。且大部分控制策略的验证只基于Matlab/Simulink 环境进行仿真,缺乏对动力学模型仿真,并不十分精确。
为了提高双电机驱动电动缸起竖系统的快速性,同时兼顾对负载扰动的鲁棒性以及双电机同步性能,本文提出了基于模糊自抗扰的双电机同步控制电动缸起竖控制策略。建立双电机驱动和电动缸起竖的数学模型,根据系统输入与输出及状态反馈设计自抗扰控制器与模糊控制器;设计交叉耦合同步控制器,实现双电机同步运行。通过Matlab/Simulink 与Adams 的联合仿真试验,将传统的PID控制、自抗扰控制、模糊自抗扰控制策略进行对比,仿真实验结果证明本文设计的控制策略对负载扰动具有更好的鲁棒性和同步性。
1 双电机同步驱动电动缸伺服系统数学模型
1.1 双电机驱动的数学模型
如图1 所示为双电机驱动电动缸伺服系统示意图。从图中可看出伺服电机通过减速器,将输出力矩传递给末端齿轮等传动机构,带动推杆行进从而完成发射架起竖过程。

图1 双电机驱动电动缸伺服系统示意图Fig.1 Schematic diagram of double motor driven electric cylinder servo system
永磁同步电机数学模型可表示为

式中:Uq,Ud,iq,id,Lq,Ld分别为交、直轴电压,交、直轴电流,交、直轴电感;ψf为转子磁链;R为定子电阻;np为电机极对数;we为电角速度;Te为电磁力矩。
经减速器后,电机力矩和减速器输出力矩关系式可表示为

式中:Jm1,Jm2,Jr1,Jr2分别为电机和减速器的转动惯量;θ1,θ2为电机的转动角度;Bm1,Bm2为动摩擦因数;M1,M2为减速器的输出力矩;i为减速器的传动比。
经小齿轮后,减速器输出力矩和小齿轮输出力矩关系式可表示为

式中:Jg1,Jg2,θg1,θg2分别为小齿轮的转动惯量和转动角度;Bg1,Bg2为动摩擦因数;Mg1,Mg2为大小齿轮间的传递力矩。
齿轮传动结构间的传递力矩可表示为

式中:Mm,Jm分别为大齿轮与推杆的驱动力矩和转动惯量;θG为大齿轮的转动角度;Bm为动摩擦因数;TL为扰动力矩;iG为大小齿轮的传动比。
1.2 电动缸起竖的数学模型
传统车载垂直起竖装置的模型如图2 所示,该系统主要由负载和起竖电动缸两部分构成。电动缸的上支耳与发射臂通过固定装置铰接,铰接点为C,发射臂上承载发射箱和导弹,此即为电动缸的负载;电动缸的下支耳和导弹车之间通过固定装置铰接,铰接点为B。当进入起竖工作状态时,电动缸通过绕起竖转轴旋转,驱动负载绕定轴转动[12-14]。电动缸起竖的受力分析简图如图3 所示。

图2 传统车载垂直起竖装置模型图Fig.2 Model diagram of traditional vehicle mounted vertical erection device

图3 电动缸起竖受力分析图Fig.3 Analysis of vertical force of electric cylinder
起竖电动缸行程和负载起竖角度对应关系式可表示为

起竖行程中力矩平衡关系式可表示为

式中:θ0为起竖前角∠BAC的值;θ为起竖角度,BC为起竖电动缸行程;AB,AC分别为铰接点之间的长度,为固定值;G,MG分别为负载及起竖架的重力和其对回转轴的重力矩;F,MF分别为电动缸对起竖架的推力以及对回转轴的力矩;l为负载及起竖架的质心与回转轴的距离;J,α为负载及起竖架对回转轴的转动惯量和角加速度。
2 模糊自抗扰控制和同步驱动控制
设计模糊自抗扰控制和同步驱动控制伺服系统,其系统控制框图如图4 所示。

图4 模糊自抗扰控制和同步驱动控制伺服系统Fig.4 Fuzzy active disturbance rejection control and synchronous drive control servo system
2.1 模糊自抗扰控制器(Fuzzy-ADRC)设计
2.1.1 自抗扰控制器(ADRC)设计
自抗扰控制器(auto disturbance rejection con⁃troller,ADRC)由能快速跟踪输入信号及其微分信号的跟踪微分器(tracking differentiator,TD)、能对系统扰动进行处理且不依赖系统具体模型的扩张状态观测器(extended state 0bserver,ESO)、将观测得到的扰动经过补偿后,得到系统的控制量的非线性状态反馈控制器(nonlinear state error feedback,NLSEF)三者组成[15-16]。
令起竖达到给定角度值时,对应大齿轮转动角度θG为系统给定输入值。系统给定输入值θG经过TD 后得到跟踪信号x1,x2分别跟踪大齿轮角度及其角速度。
依据式(4),可将大齿轮及负载动力学方程改写为
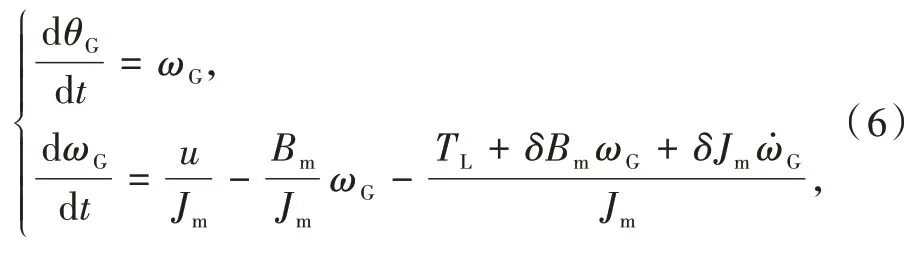
式中:ωG为大齿轮转动角速度;u为两侧电机驱动大齿轮转动的驱动力矩。设系统总扰动为f,令ẋ3=f。

因此对于双电机同步驱动电动缸起竖伺服系统,可以将系统状态方程写成:

TD 跟踪系统预设值,而过程反馈的状态量需要通过ESO 进行观测,式(8)为系统三阶ESO 表达式,其作用是:通过采集系统反馈的大齿轮转动机械角度和输入到电机的电流,实现对大齿轮端角速度以及系统扰动等信息的实时估计。

式中:β1、β2、β3为误差校正增益;a1、a2为非线性因子;δ为非线性区间宽度;y为位置测量反馈,即大齿轮转动角度;u为伺服系统输入;fal(e,ai,δ)函数可以有效避免系统产生高频振荡。
NSLEF 对ESO 实时估计得到的系统扰动进行补偿,可表示为

式中:β01为误差增益;β02为误差微分增益;b0为补偿因子。
2.1.2 模糊控制器设计
非线性状态反馈控制器(NLSEF)对伺服电机的状态反馈及电动缸起竖过程的内外扰动进行实时补偿,是自抗扰控制器的核心部分。其参数β01、β02的选取直接影响系统鲁棒性。β01、β02太小会导致系统动态响应慢,太大会导致系统刚度大,位置超调;若直接选取固定值,则很难满足起竖过程的状态变化。基于以上特点,本文设计模糊控制器,选择位移信号e1和控制信号e2作为其输入变量,β01、β02的变化量Δβ01、Δβ02为输出量,实现β01、β02在一定变化范围内进行参数自整定,有效解决自抗扰控制器参数多,难以整定的问题。
其中e1、e2的论域范围为[0,75],Δβ01、Δβ02的论域为[-5,5][15]。采用三角形函数,模糊推理模型选择Mamdani 型。参数设计采用相同的模糊规则,模糊规则表如表1 所示。其中e1、e2均分为7 个模糊子集,表示为{PB(正大),PM(正中),PS(正小),ZO(零),NS(负小),NM(负中),NB(负大)}。解模糊化采用质心法求解[15-17]。

表1 Δβ01Δβ02 模糊规则表Table 1 Fuzzy rules of Δβ01Δβ02
2.2 同步驱动控制设计
图4 中设计交叉耦合控制器,将两侧电机转速作差并经过控制器调节后,给主电机电流环负反馈输入,给从电机电流环正反馈输入,从而驱动双电机转速达到大小方向一致,实现同步。
3 仿真校验
3.1 仿真环境的搭建
在起竖过程中,传动结构中的齿轮存在齿隙,齿轮传递力矩随着齿隙变化而变化;且由式(5)可知重力矩和推杆的力矩都随起竖角度变化,转动角速度也呈非线性变化。为更精确模拟起竖过程力矩传递,本文提出了基于Matlab/Simulink 与Adams的联合仿真,即将传统PID、传统ADRC、模糊ADRC控制算法的数学模型在Matlab/Simulink 中实现,将齿轮、推杆和发射架之间的动力学仿真在Adams 中实现[18]。首先在三维仿真软件CREO 中建立发射架和包含大小齿轮、丝杆、丝杆螺母、推杆等结构的电动缸的模型,保存为parasolid 格式后导入Adams中,添加齿轮间的接触力、部件的基本运动约束及运动副,其中主要运动副为:电动缸下支耳和地面的旋转副、电动缸上支耳和发射架铰接点处的固定副、发射架底部和地面的旋转副、丝杠和大齿轮的固定副、丝杠和推杆的螺旋副,电动缸起竖模型图如图5 所示。

图5 电动缸起竖模型图Fig.5 Vertical model of electric cylinder
在Adams 中建立系统的输入输出接口,将大小齿轮输入力矩作为输入接口、大小齿轮各自的转动角度和转速、发射架起竖角度作为输出接口。将其导出成用于Matlab/Simulink 仿真的接口文件和模块,将其和Simulink 中的控制算法连接,设置仿真步长及系统仿真时间,运行联合仿真系统。其中联合仿真系统框图如图6 所示。

图6 联合仿真系统框图Fig.6 Block diagram of joint simulation system
3.2 联合仿真
仿真实验设置为模糊ADRC 控制、ADRC 控制和传统PID 控制3 种方案,对不同方案的系统响应能力和抗干扰能力作对比。观察发射架达到90°的位置曲线和齿轮1 的速度曲线。仿真中对电流限幅为-25A~+25A,交叉耦合控制器参数取2。电机和传动结构参数为:电感L为4.25 mH;电阻R为0.26 Ω;力矩系数Kt为1.066 N·m/A;反电势系数Ce为0.8 V/rad·s;减速器减速比i为10;齿轮结构传动比iG为5;负载转动惯量Jm为22.776 kg·m2;摩擦系数Bm为0.01 N·m·s/rad。
PID、ADRC 控制器参数为:电流环比例、积分系数为:0.213,13;速度环比例、积分系数为0.6,0.1;位置环比例系数为30;ESO 系数β1,β2,β3为10,50,10;ESO 系数a1,a2,δ,b0,h为1,2,0.1,100,0.01;TD系 数h,r为0.1,5;NLSEF 系 数a01,a02;δ为0.02,0.04,0.1;β01,β02初值取为40,40。
Adams 中螺旋副节圆大小选取为5 mm,且电动缸原始长度BC为3 m,大齿轮转动75 rad,电动缸伸长量为2.5 m 时发射架起竖达到90°,θ0为10°。
现给定系统大齿轮端0.1 s 到达75 rad 的阶跃位置指令信号,得到各方案下系统状态响应曲线如图7~8 所示。

图7 空载位置响应曲线Fig.7 Position response curve with no load

图8 转速响应曲线Fig.8 Rotation Speed response curve
图7~8 的仿真结果表明:由于自抗扰控制器和模糊控制器使系统抗干扰能力增强,惯性增大,Fuzzy-ADRC 和ADRC 控制方案启动和停止时能得到更快的响应速度和加速度;Fuzzy-ADRC 到位时间和ADRC,PID 相 比 分 别 提 高 了 约0.6 s 和6 s,且Fuzzy-ADRC,ADRC 和PID 的 静 态 误 差 分 别 为0.005°,0.007°和0.4°。现给定系统0.1 s 时75 rad的阶跃位置指令后,待系统稳定时40 s 处突然施加大齿轮端100 N·m 的恒定扰动力矩,得到的系统状态响应及大小齿轮转速差响应曲线如图9~10所示。

图9 恒定扰动力矩作用下位置响应曲线Fig.9 Position response curve under constant disturbance torque
图9~10 的仿真结果表明:达到稳态时Fuzzy-ADRC,ADRC 和PID 的位置跟踪误差分别为0.02°,0.12°和1.84°;Fuzzy-ADRC 调节时间短,经过0.3 s后消除外界扰动;ADRC 和PID 调节时间为4.1 s 和5 s。加扰动前Fuzzy-ADRC,ADRC 和PID 转速差幅值变化分别为-1.2~1.7 rad/s,-2~1.8 rad/s、-3.1~3.2 rad/s。加 扰 动 后Fuzzy-ADRC,ADRC 和PID 转速差幅值变化分别为-2.3~2.5,-5.1~2.3,-5~5.1 rad/s。
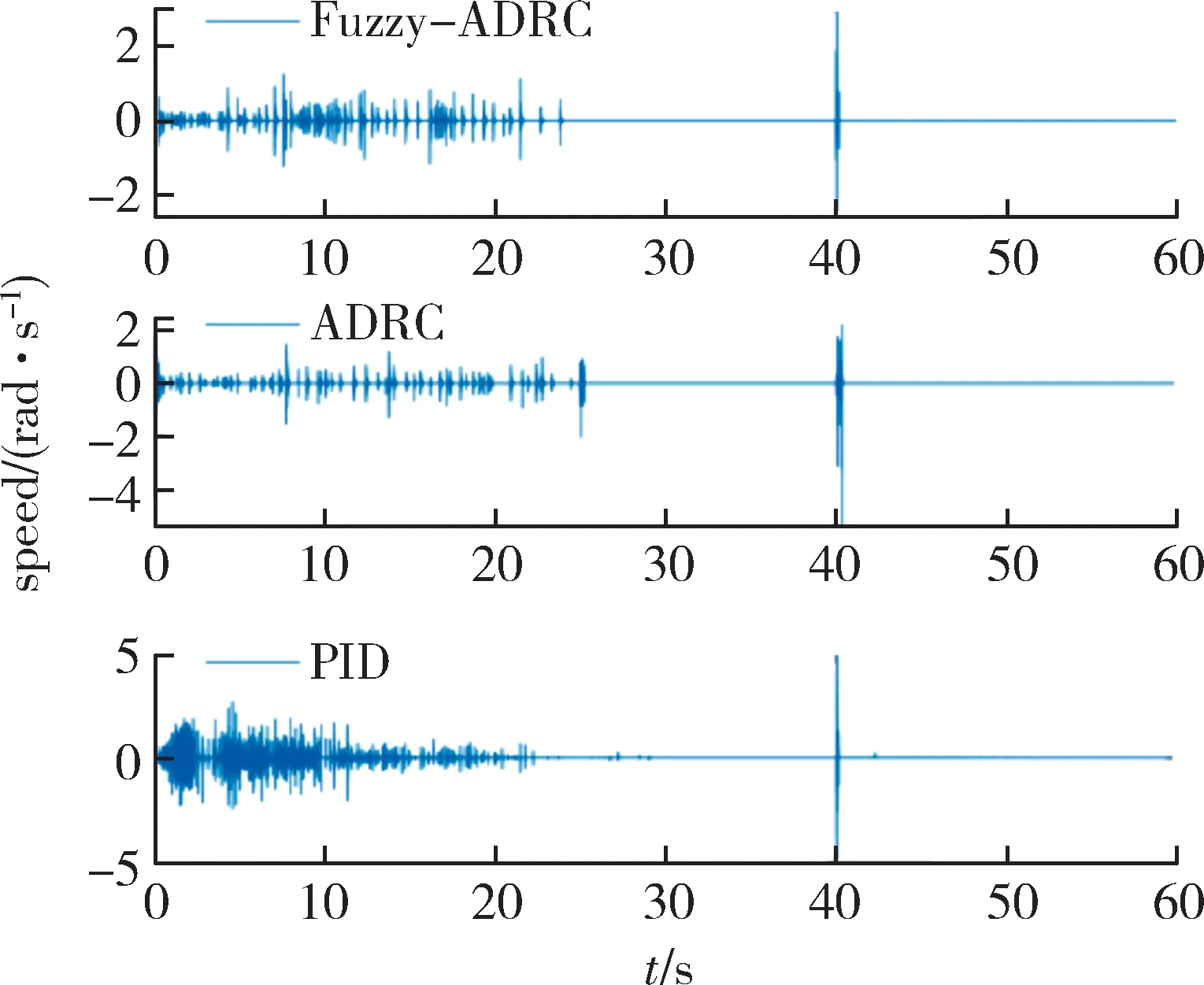
图10 恒定扰动力矩作用下转速差响应曲线Fig.10 Response curve of speed difference under constant disturbance torque
4 结束语
本文在自抗扰理论基础上,设计了基于模糊自抗扰的双电机同步驱动电动缸起竖伺服系统,在非线性反馈控制器中引入了模糊控制器,具有调试简单,可实用性强、具备参数自整定等优点。采用联合仿真的方式,更精确地模拟起竖过程负载力矩变化。仿真实验结果表明:Fuzzy-ADRC 对比传统ADRC 和PID,动态响应速度分别提升了2.38%和20%,稳态精度分别提高了0.002%和4.3%;Fuzzy-ADRC 对比传统ADRC 和PID,对转矩负载扰动的动态响应速度分别提升了92%和99%,稳态精度分别提高了0.1%和2%。在起竖过程和转矩负载条件下,Fuzzy-ADRC 双电机同步性能对比传统ADRC 和PID 也均有提升。对双电机同步驱动电动缸起竖系统,本文设计的基于模糊自抗扰的控制策略提升了系统的动态静态响应,且对负载扰动具有更强的鲁棒性及同步性。
