变刚度CFRP层合板在低速冲击下的分层失效分析①

牛雪娟，李辰阳，刘江雨

(1.天津工业大学 机械工程学院，天津 300387；2.天津市现代机电装备技术重点实验室，天津 300387)

0 引言

碳纤维复合材料具有比模量高、比强度高、比刚度高、抗疲劳性能强等优势，在航天工程、民用飞机、高端汽车、高速列车等领域有非常广泛的应用。其在各个应用领域、工况下都有可能受到冲击作用而引起整个结构的安全性降低，因此，冲击损伤对复合材料的使用安全造成的影响一直是国内外学者们研究的重要领域，且具有非常重要的实际意义。

近几年，众多学者在复合材料结构件渐进损伤方面已取得较成熟的研究成果。王威力等研究了在低速冲击载荷下纤维增强材料不同的复合材料之间损伤情况的差异。武海鹏等研究了复合材料损伤后的剩余强度，并分析了纤维种类、层合板结构形式对复合材料层合板损伤容限的影响。在低速冲击研究方面，段苗苗等对40层层合板进行冲击试验，在考虑分层和基体损伤的基础上另外研究了凹坑深度与冲击能量的非线性关系。复合材料层合板变刚度的铺放轨迹直接影响了结构件的性能，对变刚度层合板的铺放轨迹学者们也有众多研究方向。王琥等根据当前变刚度材料的发展现状和研究成果，从优化分析和制造等方面进行了研究。GÜRDAL等首先提出了纤维角度线性变化方法，利用数学公式描述了从板中心到边界纤维角度的连续变化趋势。牛雪娟提出了一种基于流场函数的轨迹设计方法并验证了设计方法的实用价值。卫宇璇等研究了三种变刚度铺放轨迹，分析得出特定参数的二次Bezier曲线的抗屈曲性能最佳。

以上研究工作中，关于变刚度曲线铺放改善结构件抗冲击性能的研究较少也均没有对分层损伤进行探讨。本文采用三维Hashin准则来判定损伤的起始，采用Cohesive粘聚区实现复合材料层间的失效模拟，验证通过变刚度曲线铺放的方法提高层合板的抗冲击性能的可行性。

1 冲击过程中的失效

1.1 面内损伤及损伤起始准则

本研究中采用三维Hashin损伤起始准则，具体描述如下：

(1)纤维拉伸模式(≥0)

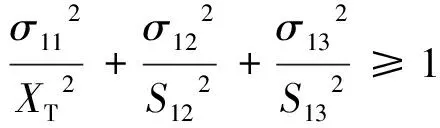
(1)

(2)纤维压缩模式(<0)

(2)

(3)基体拉伸模式(+≥0)

(3)

(4)基体压缩模式(+<0)

(4)

式中为1方向即纤维方向的拉伸强度；为1方向的压缩强度；为2方向即面内垂直于纤维方向的拉伸强度；为2方向压缩强度；、、分别为剪切强度。

1.2 层间分层失效及损伤起始准则

采用Cohesive粘聚区实现复合材料层间的失效模拟，称为内聚力模型。本文采用二次应力准则作为层合板层间失效的起始判据，具体的损伤起始判据如式(5)：

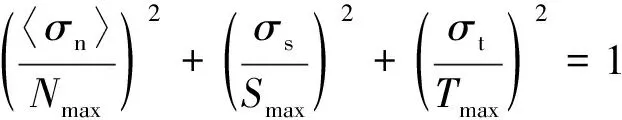
(5)

式中为层间正应力；、分别为两个方向的剪切应力；、、分别对应层间拉伸和剪切最大强度；≤0时，〈〉取值为0，即受压不会产生层间的分层损伤。

1.3 刚度退化方式

刚度退化方式一般分为两类，一种是直接将材料的模量瞬时折减为一个较小的值或折减为0，这种退化方式会造成层合板的提前失效，误差较大。另一种是刚度连续退化方式，此类退化方式更符合实际情况，本文采用连续退化模式中的线性连续刚度退化方式进行分析。

(6)

内聚力模型的损伤演化规律采用基于BK混合模式的能量准则。

(7)

式中、、分别为Ⅰ型、Ⅱ型、Ⅲ型裂纹对应的应变能释放率；、、分别为Ⅰ型、Ⅱ型、Ⅲ型裂纹对应的临界应变能释放率；为损伤因子，一般在0.5～2.0之间取值，本研究与参考文献[9]取值一致，=1.45。

2 变刚度复合材料层合板

2.1 预浸料窄带曲线铺放

现如今自动铺丝技术AFP正在高速发展，采用AFP技术可以实现层合板刚度连续变化，这种复合材料层合板称为变刚度复合材料层合板。

变刚度复合材料层合板的曲线铺放路径会直接影响产品的力学性能。GÜRDAL和OLMEDO提出了纤维角度线性变化的方法，该方法的纤维角度沿参考坐标方向的线性变化趋势如下：

(8)

式中为纤维轨迹的特征长度；为纤维在参考坐标下原点位置的方向角度，即纤维在原点处的切线与轴形成的夹角；为纤维在特征长度处的方向角度。

根据曲线斜率与切角之间的关系，可将函数表达为如式(9)关系式：

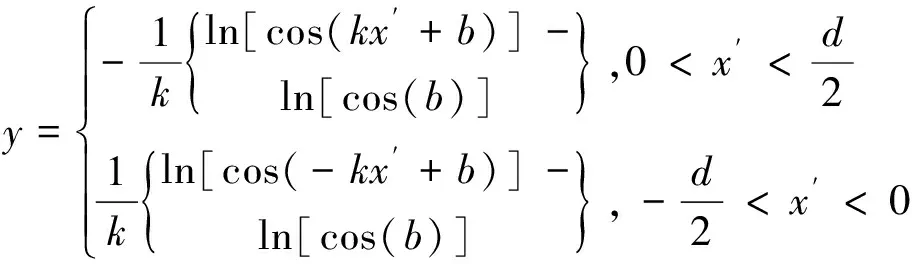
(9)

在总体坐标系中，层合板中任意一点的纤维角度为

(，)=Ø+()

(10)

其中，Ø为参考坐标轴与总体坐标轴的夹角，如图1所示。

图1 角度线性变化纤维路径示意Fig.1 Schematic diagram of fiber path withlinear angle change

2.2 基于VUMAT子程序的层合板低速冲击响应特性分析

2.2.1 VUMAT子程序分析

有限元软件Abaqus中存在两个常用的求解器，即Abaqus/standard隐式求解器和Abaqus/explicit显式求解器。在低速冲击情况中使用显式求解器更为适合，它的计算方式无需迭代，各增量步都可以保证收敛。本文针对落锤冲击试验模型，采用显式求解器进行分析。通过VUMAT来定义材料本构关系、面内损伤起始准则以及损伤演化准则。

2.2.2 算例仿真分析

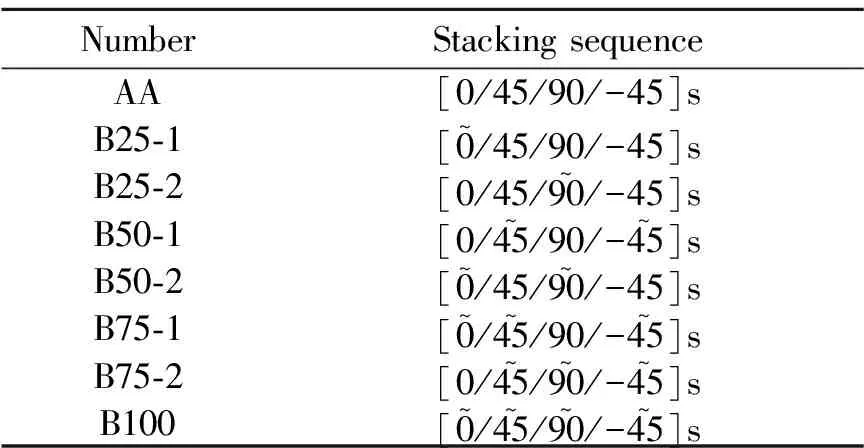
表1 层合板铺层方式

图铺层材料方向设置示意Fig.2 Schematic diagram of laying orientation of variablestiffness laminate

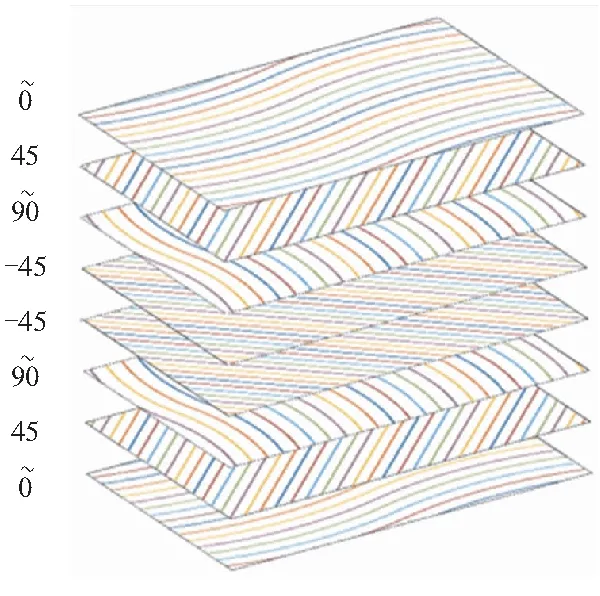
图3 B50-2变刚度层合板铺层示意Fig.3 Schematic diagram of B50-2 variable stiffnesslaminate layer

本文中为研究纤维曲线铺放与直线铺放复合材料层合板在受到载荷时的对比效果，选取纤维铺放角度的变化走势与直线铺放角度相同的铺层顺序。此种方法增加了层合板铺层结构的可设计性，限制了纤维角度变化的具体数值，同时与常刚度层合板的对称铺层结构保持铺层顺序一致，方便组间进行比较，研究在同一种纤维角度变化的情况下，不同变刚度铺层百分比对抗冲击性能的影响。

由于变刚度层合板所用材料与传统层合板一致，且角度固定从而限制了曲率，保证了纤维体积百分比变化不大，因此可假设变刚度层合板厚度均匀且界面属性与常刚度层合板相同。通过将坐标相同的单元赋予相同材料方向的方式，来模拟平移法预浸料铺放。在层间插入0厚度的内聚力单元模拟层间界面。假设冲头与支座为刚体，冲头为直径16 mm的半球形圆柱体，质量为2 kg，冲头初速度为5 m/s，方向延轴指向层合板表面，模拟25 J的冲击能量。使用中心镂空125 mm×75 mm的底座支撑复合材料层合板并将层合板4个角的轴方向位移限制为0来模拟边界条件。所有接触采用通用接触，法向属性硬接触，切向属性摩擦系数为0.3。建立的模型如图4所示；单向板的材料参数如表2所示，层间界面的材料参数如表3所示。表2中、(s=‘f’或‘m’)分别为纤维或基体的拉伸、压缩能量释放率，参与子程序中刚度退化的计算。

(a)Frontview (b)Backview图4 低速冲击Abaqus有限元模型Fig.4 Abaqus finite element model for low velocity impact

表2 复合材料参数

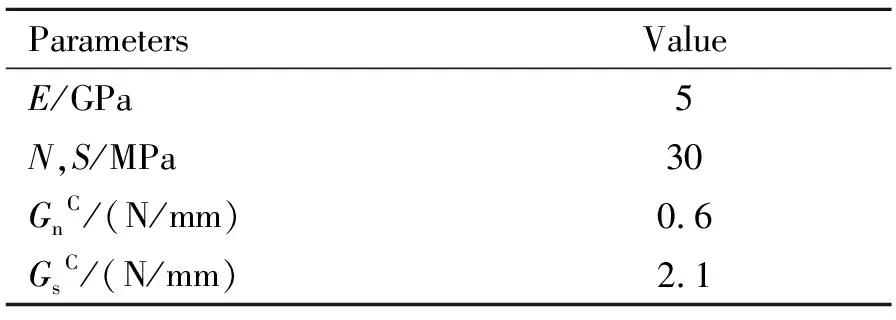
表3 层间界面材料参数

3 分析结果

通过有限元仿真得到了8组层合板在冲击载荷下的冲击力-时间、总动能-时间、冲头位移-时间曲线，并进一步分析了各组层合板冲击响应、分层损伤和应力分布的情况。

3.1 冲击力学响应分析

图5、图6分别为25 J冲击能量下各组层合板的冲击力-时间、冲头位移-时间曲线；图7为总动能-时间曲线。在冲击过程的初期，层合板受到冲击后产生振动，冲击力随着时间增加而逐步震荡上升。随着冲击时间的增加，冲击力变大，层合板内部造成损伤。峰值过后冲头开始反弹，冲击力逐渐减小至0，冲头离开层合板表面。

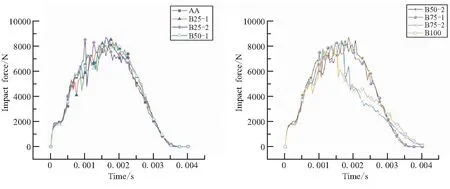
(a)AA，B25-1，B25-2，B50-1 (b)B50-2，B75-1，B75-2，B100图5 冲击力-时间曲线Fig.5 Force vs time curves

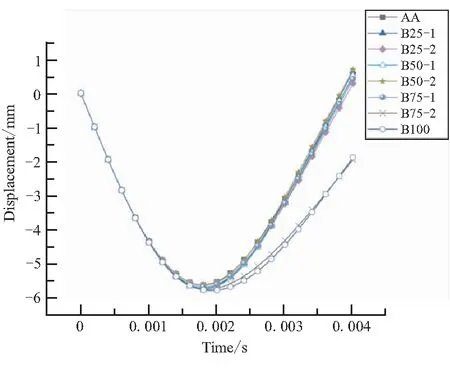
图6 冲头位移-时间曲线Fig.6 Displacement vs time curves

图7 总动能-时间曲线Fig.7 Total kinetic energy vs time curves

AA、B25-1、B25-2、B50-1、B50-2、B75-1六组层合板冲击力下降的时间明显晚于B75-2、B100两组层合板，且B75-2、B100两组层合板出现了明显的骤降现象，说明B75-2、B100两组层合板较早发生了严重损伤且抗冲击性能比其他组层合板更弱。

结合图5、图6、图7和表4可以得出，B25-1、B50-1、B50-2因抗弯刚度相对AA组常刚度层合板较低而吸收的能量较少，其中B25-1吸收能量最少，为10.61 J。

表4 层合板冲击特性

冲头与层合板接触时间的长短与损伤面积有关，接触时间过长会导致损伤面积变大，上述三组层合板吸收能量大小相近，但B50-2组层合板与冲头接触的时间最短，层合板承受冲击载荷峰值和最大位移的时间也最短，损伤面积也略小于另外两组层合板。另外B75-2、B100吸收的能量更多，且接触时间明显大于其他组层合板，因此发生了更严重的损伤。说明了不同层合板在吸收能量相似时，冲击力峰值持续时间与损伤情况存在正相关关系。

3.2 应力分布分析

从图5可以看出，各组层合板冲击力峰值出现在0.002 s左右，对比在0.002 s时各组层合板底层Cohesive的应力分布情况，图中红色区域表示应力集中区域，如图8所示。变刚度层合板可以改变层合板的面内刚度，不均匀的冲击力载荷在变刚度层合板平面上可以沿着预浸料曲线铺放轨迹良好分布。变刚度铺层百分比为25%的两组变刚度层合板应力分布与AA常刚度层合板相似。变刚度铺层百分比为50%、75%、100%的变刚度层合板底层应力分布相比AA常刚度层合板有明显的扩散现象，但B75-2和B100两组层合板的应力集中区域仍然处于层合板中心，容易造成分层损伤的完全失效。B50-1、B50-2、B75-1不仅出现了良好的应力扩散，而且应力集中的位置沿着曲线纤维的角度延伸，避免了在冲击中心处造成应力集中而产生更严重的分层损伤。

结合各组层合板的冲击力学曲线与应力分布情况，变刚度铺层百分比为25%时，改变0°铺层为曲线铺放的变刚度层合板的抗冲击能力强于改变90°铺层的变刚度层合板。变刚度铺层百分比为50%时，改变0°、90°铺层为变刚度的层合板的抗冲击能力略微高于改变±45°铺层的变刚度层合板。变刚度铺层百分比为75%时，改变0°、±45°铺层为曲线铺放层合板的抗冲击能力明显强于改变±45°、90°的变刚度层合板。

3.3 分层损伤分析

通过Abaqus仿真分析得到8组不同层合板在25 J能量下低速冲击后的分层损伤情况。其中变刚度铺层百分比为50%的层合板吸收能量较少，且与冲头接触时间最短，因此分层损伤面积最小且刚度退化率低，层合板底层没有出现完全损伤。变刚度铺层百分比为25%的两组分层损伤情况与AA常刚度层合板相近，变刚度铺层百分比为75%和100%的三组层合板比常刚度损伤更严重，这是因为层合板与冲头接触时间过长导致。说明并不是所有变刚度铺层结构的层合板都可以提升抗分层损伤的能力。

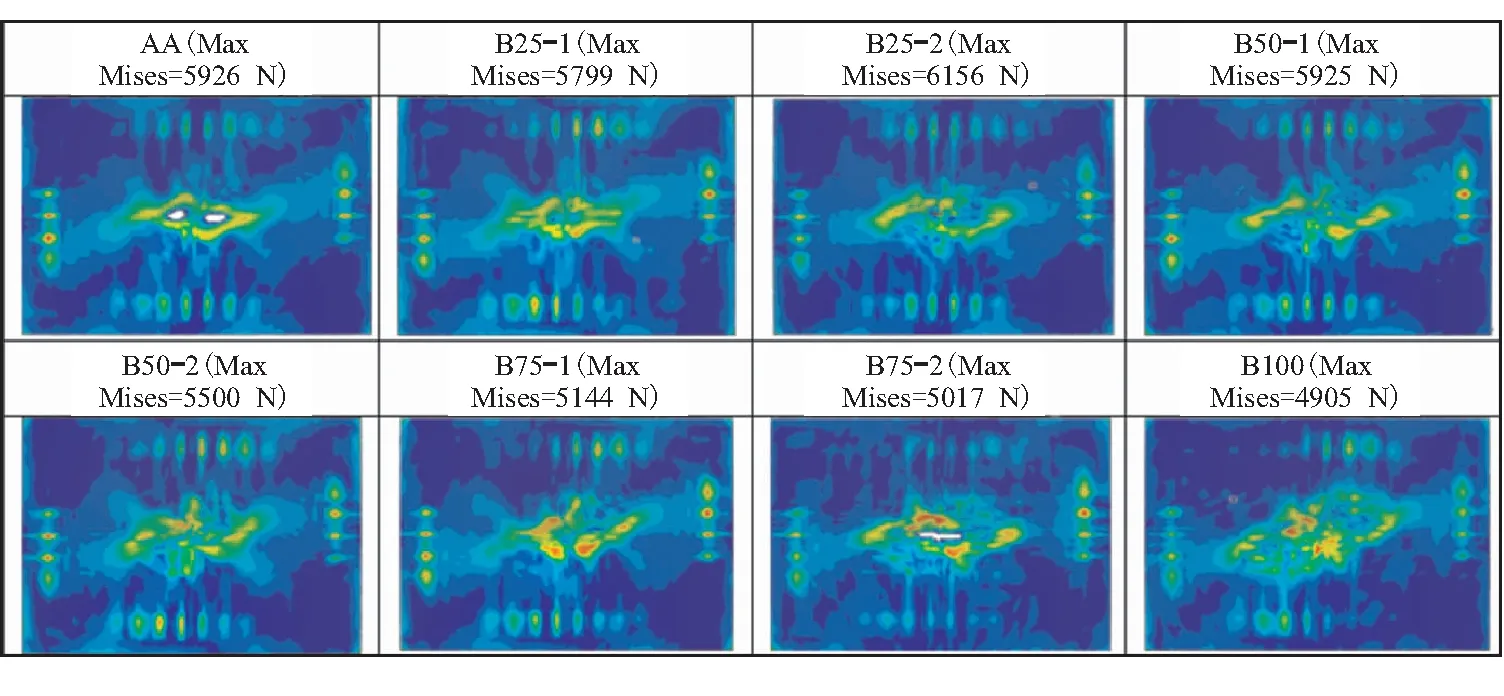
图8 冲击力峰值0.002 s时层合板底层应力分布对比Fig.8 Comparison of stress distributions at the bottom layers of laminate whenthe peak impact force is 0.002 s

图9为AA常刚度层合板与B50-2变刚度层合板分层损伤对比图，与冲头最先接触的为第一层。从图9中可以看出，两组层合板的前三层分层损伤区别不明显，但从第五层可看出B50-2组变刚度层合板分层损伤完全失效且被删除的单元面积明显小于AA组常刚度层合板，AA组被删除单元面积占层合板总面积的3.06%，B50-2组变刚度层合板为0.49%，完全失效面积减少了层合板总面积的2.57%。第七层中AA组层合板完全损伤面积为0.22%，而B50-2组层合板没有出现完全损伤。由此可知，B50-2组变刚度层合板相比AA组常刚度层合板在低速冲击下抗分层损伤的性能更好。

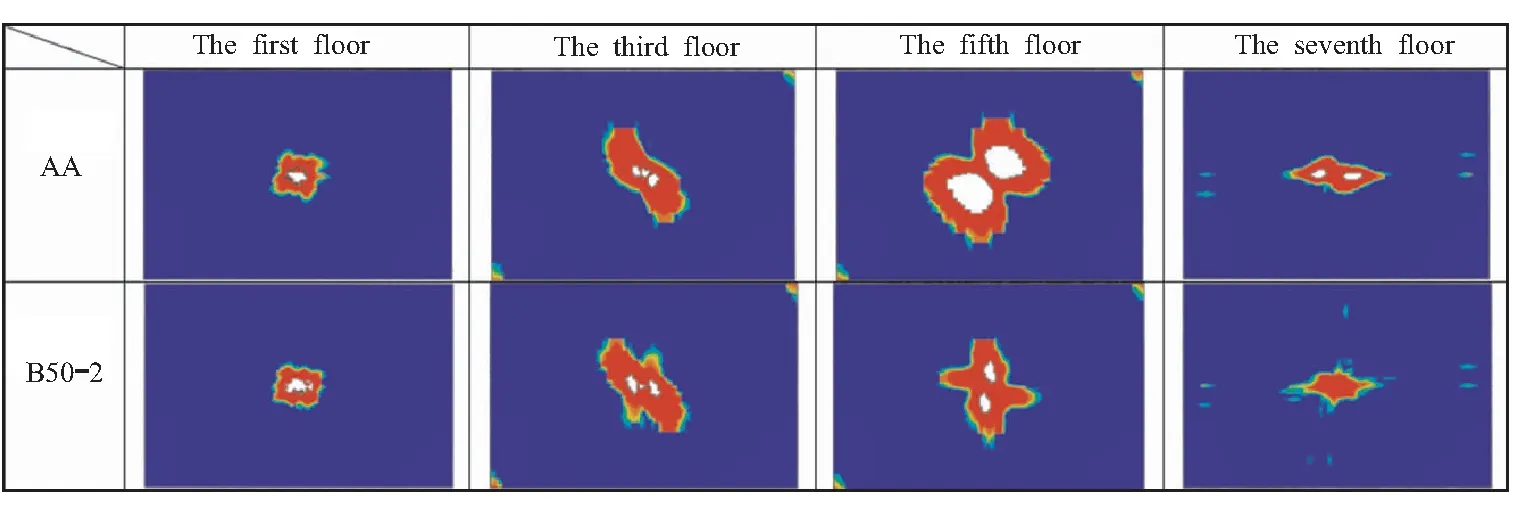
图9 层合板AA与B50-2分层损伤对比Fig.9 Comparison of delamination damage between laminates AA and B50-2

4 结论

通过对比不同组变刚度层合板与常刚度层合板之间的冲击力学响应、应力分布和分层损伤情况，研究了变刚度层合板的抗冲击性能。

(1)具有变刚度铺层结构的层合板可以改变层合板的抗弯刚度、缩短冲头与层合板的接触时间，因而可以减小吸收的动能并大大改善层合板的抗分层损伤能力，且越靠近冲击背面抗分层损伤能力提升越大。

(2)在吸收能量相近时，与冲头接触时间更短的层合板造成的分层损伤更小，变刚度铺层百分比为50%的层合板相比常刚度层合板的单层损伤面积最多可减少2.57%。

(3)不均匀的冲击力载荷在变刚度层合板面内可以沿着预浸料曲线铺放轨迹良好分布，避免了在冲击中心处的应力过度集中而造成分层损伤的完全失效。

(4)变刚度层合板的抗分层损伤能力与层合板吸收的能量、抗弯刚度以及冲头与层合板接触的时间有关。本文相关研究结果对变刚度层合板抗冲击的设计和优化有一定参考意义。