柔性喷管用弹性件材料动态力学性能试验与数值模拟①
2022-07-11李定机毛成立
李定机,毛成立,郑 庆,童 悦,马 超
(1.上海航天动力技术研究所,上海 201109;2.上海市塑料研究所有限公司,上海 201702)
0 引言
柔性喷管是固体火箭发动机推力矢量控制的结构形式之一,柔性接头作为其关键部件,对柔性喷管的摆动特性有重要影响。柔性接头一般由金属增强件、橡胶弹性件、前后法兰构成,前后法兰中间包夹着数层增强件与数层弹性件交替层叠粘接的结构,从而形成可全轴摆动结构。橡胶材料在不同形式的载荷下表现许多与金属材料不同的力学特性,如Payne效应、Mullins效应、超弹性以及粘弹性的应力松弛、蠕变、迟滞等。导弹飞行过程中,在燃气高压、伺服机构驱动的联合动态载荷作用下,柔性接头结构内部受力情况较为复杂,对摆动力矩特性具有决定性影响的弹性件橡胶会表现出复杂的几何、材料双重非线性。因此,对弹性件材料力学行为的研究是柔性喷管静态、动态力矩特性计算的重要基础。
SHANI等在计算其设计的柔性接头摆动力学性能时,在有限元程序中直接采用线弹性的假设对弹性件材料进行建模,弹性件在计算中的剪切模量被设为恒定值。王成林等及史宏斌等采用弹簧单元模拟柔性接头弹性件的力学行为,弹簧单元的刚度系数矩阵来自喷管摆动试验的摆动刚度。文献[4-12]从弹性件材料本构出发,通过材料的基础力学试验确定了基于唯象理论的超弹性本构模型来描述弹性件的非线性弹性行为。目前,相关文献资料中对柔性喷管弹性件建模都是基于线弹性或非线性超弹性的理想模型,适用于描述静态或准静态过程中的弹性行为,由于未考虑材料的粘弹性性质,因此无法描述动态过程中与时间相关的各类力学行为。
本文针对柔性喷管用弹性件橡胶材料,建立了橡胶材料的超-粘弹性模型,进行不同加载速率和不同应变水平的试验研究,并通过试验验证该模型和方法在模拟弹性件材料动态迟滞行为上的有效性,从而为后续柔性接头动态特性的计算研究提供材料层面的建模方法。
1 超-粘弹性本构模型的建立
1.1 超弹性模型
橡胶通常被认为是不可压缩的各向同性材料,其应力-应变的本构关系由含应变能函数W偏导项的等式描述,如式(1)所示。

(1)
式中为主应力;为应变能函数;为主伸长比;,分别为第一应变、第二应变不变量;为静水压强。
目前,有大量关于超弹性本构方程的研究,按机理可分为两大类,即基于连续介质力学的唯象理论和基于分子结构和构象熵改变的统计理论。在数值模拟中,常用的模型有Ogden、多项式模型及缩减多项式模型。在不可压缩的假设下,一些常用的唯象理论模型的应变能函数如下:
Mooney-Rivlin:
=(-3)+(-3)
(2)
Neo Hooke:
=(-3)
(3)
Yeoh:

(4)
Ogden:

(5)
对于材料的单轴拉伸(UT)、平面拉伸(PT)和双轴拉伸(ET)三种变形状态而言,其Cauchy应力可通过应变能的偏导数形式表示成式(6)~式(8),从而能通过各类试验来确定应变能表达式中的各个材料系数。

(6)
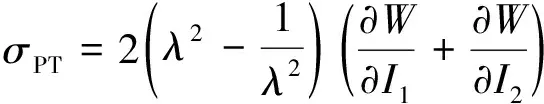
(7)

(8)
1.2 超-粘弹性模型
将粘弹性引入本构模型中,考虑时间相关性从而计算材料动态的特性。常用的超-粘弹性模型的建立方式是通过粘壶和弹簧单元的串联和并联构造一个力学单元,以模拟材料的弹性和粘性。BERGSTRÖM等从高分子链的蠕动运动出发,推导建立了非线性超-粘弹性模型。模型网络如图1所示,由平行的A 网络和B网络部分构成,A网络能够描述力学单元平衡状态下的响应,而B网络则描述时间影响下偏离平衡态的响应。两个网络的应变梯度张量相同,即==,二者贡献的应力之和即为模型的瞬时应力。
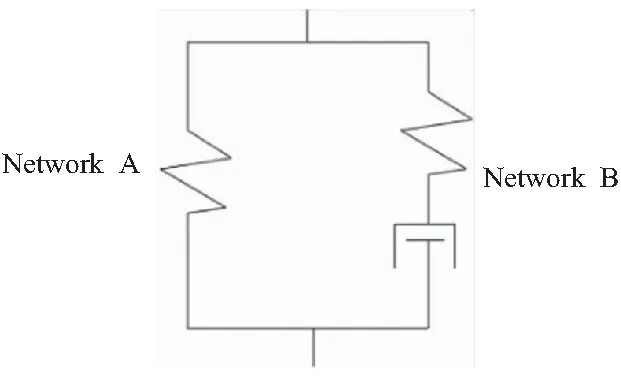
图1 Bergström-Boyce网络模型示意图Fig.1 Schematic of Bergström-Boyce network model
基于超弹性应变能函数理论,网络中的弹性部分的本构关系形式如式(1)所示,描述与时间无关的应力-应变关系。
而粘性效应由式(9)所示的等效应变率描述:
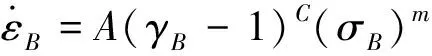
(9)
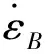
另外,还需要定义应力比例因子,其意义是在瞬时载荷作用下,B网络和A网络承载的应力大小之比。
2 弹性件材料力学试验
对于弹性件使用的橡胶材料来说,需要通过材料基础力学试验确定所使用的超弹性模型及其参数,这些试验包括单轴拉伸和压缩、双轴拉伸和压缩以及平面拉伸和压缩试验。考虑到柔性接头的变形形式主要是剪切变形,并在拟合过程中,除了缩减多项式模型,Ogden模型和Mooney-Rivlin模型均需要两种及以上的变形类型试验数据,以得到确定的材料参数。因此,本文采用单轴拉伸试验和四板剪切试验研究弹性件材料的力学性能。
单轴拉伸试验方法参照GB/T 528—2009,选择总长度75 mm、厚度2 mm、中间宽度4 mm的Ⅱ型哑铃型试样;四板剪切试验方法得到参照GB/T 12830—2008。两种试验均在电子拉力机上完成,如图2所示。

(a)Uniaxial tensile test (b)4-slice shear test图2 单轴拉伸和四板剪切试样Fig.2 Uniaxial tensile specimen and 4-slice shear specimen
为了研究Mullins效应对该橡胶材料的影响,需要对试件进行数次加载循环,对单轴拉伸试件和四板剪切试件分别进行4次加载循环得到图3和图4的应力-应变曲线。由多次加载的曲线可以看出,对于两种不同的变形形式来说,材料第一次加载和第二次加载的应力-应变曲线,都有显著差异。在相同的应变下,第二次加载的应力相较于第一次加载的应力来说显著减小,而在第二次加载之后,应力-应变曲线则逐渐稳定下来。其中,单轴拉伸的第一次加载和第二次加载曲线之间差异较大,第二次加载应力值相比第一次最大减少了50.6%;拉伸应变在0%~150%的范围内,应力稳定较快,在该应变区间内可以选择第三次或第四次的数据进行拟合,但应变超过150%时则需要更多次数的试验来确定更稳定的应力曲线;相比而言,剪切变形的第一次和第二次加载之间的差异相对更小,第二次加载应力值相比第一次最大减少了27.1%,并且应力值在更少的加载次数下能达到更稳定的状态。因此,剪切试验进行3次加载循环就可确定应力软化后的曲线。
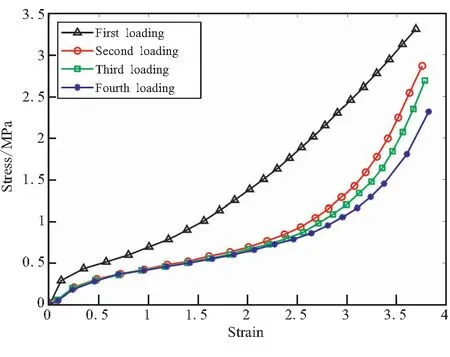
图3 单轴拉伸机械调节Fig.3 Mechanical adjustment on uniaxial tensile specimen

图4 四板剪切机械调节Fig.4 Mechanical adjustment on 4-slice shear specimen
由于柔性接头在工作过程中需要连续、多次摆动,因此应当采用机械调节之后的应力-应变数据拟合超弹性模型,即对试样进行4次重复加载,并记录每次应力-应变,取最后一次加载时的应力-应变,以消除Mullins效应。分别取图3和图4中最后一次加载曲线,并取二者同应变范围内数据以提高拟合准确度,如图5所示,采用此数据用于拟合本构模型。Abaqus中超弹性参数的拟合需要平面拉伸的试验数据来描述材料的剪切变形性能,而本文采用的是四板剪切的试验。二者的区别在于前者是纯剪切的变形形式,后者则是简单剪切的变形形式,简单剪切可以看作是一种纯剪切加上转动的变形形式。因此,在拟合之前要对数据进行转换。参考文献[14]可以推导出简单剪切和纯剪切的应力-应变关系如下:

(10)
式中,分别为四板剪切获得剪切应变和剪切应力;、分别为平面拉伸的名义应变和名义应力。

图5 超弹性模型拟合所用数据Fig.5 Data for fitting hyperelastic model
柔性喷管在不同的摆角幅度和摆动速率下,表现出的力矩特性也不同。为了研究柔性喷管往复摆动过程中的动态力矩特性与弹性件材料动态力学特性的关联性,本文基于四板剪切试验形式,在不同速率和不同最大应变水平的试验条件下进行了剪切加载回复试验。按照本文所研究柔性接头的尺寸估算弹性件在在摆动到较大角度6°和中等角度3°时的最大剪切应变分别对应四板剪切试验70%和150%的应变水平;而估算柔性接头在中等摆角3°时,在1、0.5、0.1 Hz的摆动频率下,剪切应变速率分别对应四板剪切试验加载速率为420、240、50 mm/min时的剪切应变速率。因此,从上述估算得到的2个应变水平和3个速率水平中选择并组合,形成四板剪切动态试验的加载工况,图6是四板剪切试件以240 mm/min的加载速率分别加载到应变为150%和70%时,再以相同速度回复的迟滞曲线,图7是四板剪切试件分别以420、240、50 mm/min的加载速率加载到应变150%附近的迟滞曲线。
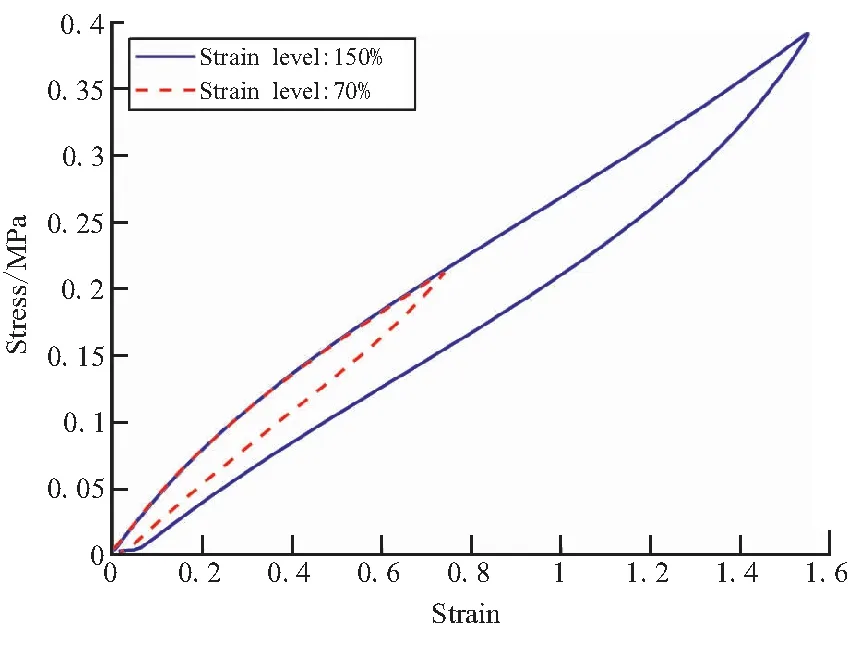
图6 不同应变水平下四板剪切迟滞曲线Fig.6 Shear hysteresis curve at differentstrain levels

图7 不同加载速率下的四板剪切迟滞曲线Fig.7 Shear hysteresis curve at differentrates of loading
迟滞曲线围成的面积表示材料在一个加载循环周期内的能量损耗,这种损耗和材料的粘弹性密切相关。为了量化能量损耗大小,将迟滞环包络面积与加载段曲线和应变轴所围面积之比值定义为一个循环加载过程中的能量损耗率。从图6中70%和150%应变幅度的迟滞曲线面积可以看出,应变幅度对能量损耗的影响很大,随着最大应变的增加,循环过程的能量损耗增大,这主要是由于阻尼力做功的行程增加了,70%和150%应变条件下的能量损耗率分别为21.59%和17.59%。图7反映了应变速率对迟滞曲线的影响,随着加载速率的增加,加载在试件上的载荷也随之增加。而随着变形的增大,加载速率对载荷的影响也越来越显著,在应变为150%时,加载速率为240 mm/min和50 mm/min的曲线应力值分别相比于加载速率为420 mm/min的曲线对应应力值下降了4.24%和6.03%。而在所研究的加载速率范围内,能量损耗的变化不大,三个速率下能量损耗率为21.46%,21.59%和21.44%。这些应变幅度和应变速率对材料力学性能的影响规律与文献[7]中所描述的摆动幅度和摆动频率对柔性接头力矩特性的影响规律是一致的。因此,针对弹性件材料本构进行建模,通过数值计算的方法可预示柔性接头的静态、动态力矩特性。
3 模型参数确定
3.1 超弹性模型参数的确定
根据图5中的单轴拉伸和四板剪切的试验数据,分别使用2阶Ogden、3阶Ogden、Mooney-Rivlin、Neo Hooke和Yeoh模型进行拟合,得到的原始数据与拟合曲线的对比图如图8和图9所示。

图8 单轴拉伸拟合结果Fig.8 Curves fitting to uniaxial tensile test
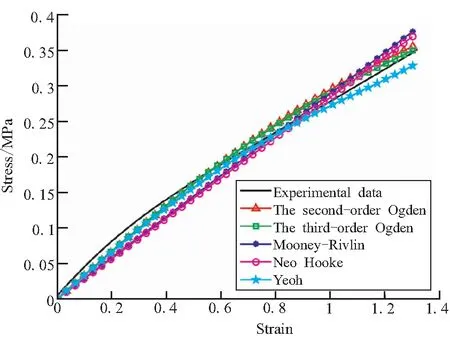
图9 剪切拟合结果Fig.9 Curves fitting to simple shear test
对于单轴拉伸,Ogden模型相比多项式及缩减多项式模型更为逼近试验数据;而对于四板剪切,列出的模型拟合效果较好,其中最大的平均误差不超过20%。为了比较超弹性本构模型拟合单轴拉伸应力-应变和剪切应力-应变的整体效果,利用组试验-预测数据可以计算拟合的归一化残差,同时考虑模型对单轴拉伸和四板剪切的整体预测效果,则整体残差如式(11)所示。

(11)
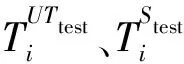
采用式(11)计算得到表1中各个模型的整体残差,由此判断采用3阶Ogden模型时整体拟合效果最好,相应的材料参数在表2中列出。根据Drucker稳定性条件可知,这组本构参数在所研究的应变范围内能够保证材料计算的稳定。

表1 超弹性模型预测单轴拉伸和剪切的整体残差

表2 三阶Ogden模型材料参数
3.2 粘弹性模型参数的确定
粘性部分的材料参数具有相互耦合的特点,因此文献[16-17]中给出了该模型下一般弹性体的粘性部分参数,即=5,=-1,=4,并建议从给出这组一般性参数出发,采取试错法改变参数,以使得计算结果符合试验曲线。为节省时间和成本,本文利用Python对Abaqus进行了二次开发,实现了参数化建模和计算结果的自动化处理。采用模拟退火算法,将材料参数和作为设计变量,将计算得到的应力-应变曲线和试验的应力-应变曲线的平方误差作为目标函数,编写了相应的脚本,迭代优化后得到如表3的材料参数。

表3 粘弹性模型材料参数
4 计算与结果分析
4.1 有限元模型的建立
在Abaqus中建立与试验中所使用试件同尺寸的有限元模型,如图10和图11所示,分别为单轴拉伸试件和四板剪切试件的网格划分以及边界条件加载情况。橡胶部分均应用C3D8H杂交单元以适应橡胶的不可压缩性,刚性板则采用C3D8R单元。另外,在四片刚性板中央分别定义参考点,基于这些参考点定义刚性板的刚体约束以节约计算资源。分析采用Dynamic,Implicit过程求解,以计算与时间相关的力学行为,利用表2和表3的参数定义橡胶的材料属性。

图10 单轴拉伸试件计算网格Fig.10 Computation grids on uniaxialtensile specimen
4.2 模型计算检验
采用第2节中建立的超-粘弹性模型进行计算,超弹性部分采用三阶Ogden模型,粘性部分采用Bergstrom-Boyce迟滞模型。试件达到最大位移时的应力云图如图12和图13所示,应力的分布符合实际标准件的变形规律。由于柔性喷管摆动时弹性件主要应变形式为剪切应变,故下文只针对剪切形式变形进行计算仿真。分别在加载速率为420、240、50 mm/min的条件下进行最大应变水平为100%的四板剪切试验和对应的仿真计算,得到如图14所示的应力-应变曲线。试验和计算结果呈现出一致的规律,即随着加载速率减小,应力值也减小,尤其是在应变较大的区域,加载速率对剪切应力的影响更为明显,而应变较小时加载速率对剪切应力几乎没有影响。三个加载速率下的计算结果与试验的平均误差均不超过8%。
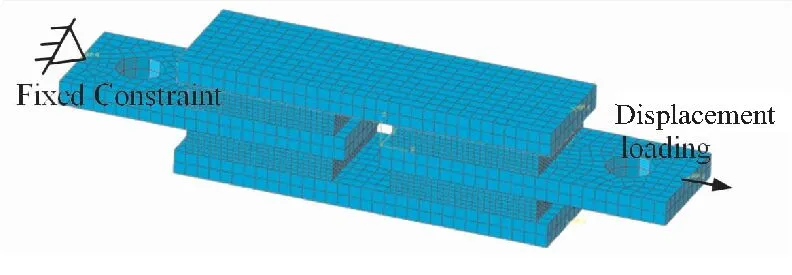
图11 四板剪切试件计算网格Fig.11 Computation grids on 4-slice shear specimen

图12 单轴拉伸应力云图Fig.12 Stress contour of uniaxial tensile simulation
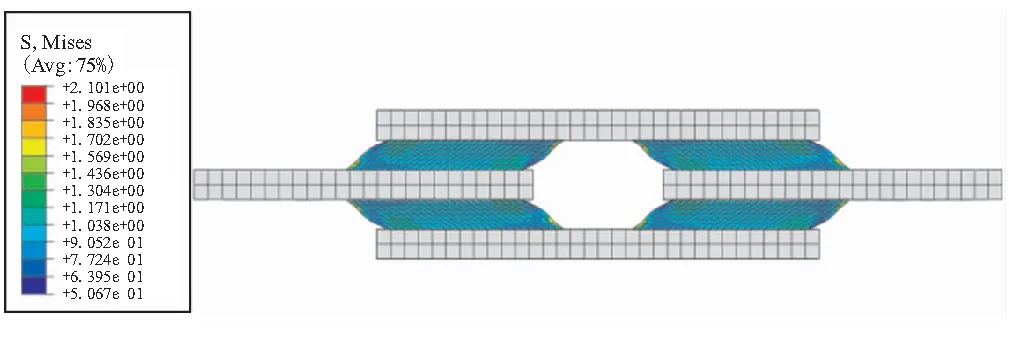
图13 四板剪切应力云图Fig.13 Stress contour of 4-slice shear simulation

(a)420 mm/min (b)240 mm/min (c)50 mm/min图14 不同剪切速率下的剪切试验与仿真对比Fig.14 Comparison between test and simulation of 4-slice shear at different rate of loading
在四板剪切有限元试件上施加速率为240 mm/min位移边界条件,在位移达到5.6 mm,即70%应变时再以相同速度回复到零位移处,以模拟四板剪切加载回复循环的试验。模拟计算的应力-应变数据与试验数据对比如图15所示,计算结果与试验数据吻合较好,迟滞曲线形状一致,曲线包围面积相对误差21.3%。由于该模型没有考虑材料塑性,无法反映永久形变,导致曲线在原点附近的小应变范围内相对误差较大,因此除去应变0.05以下的数据点,模型计算结果的平均相对误差为9.80%。说明所使用的超-粘弹性模型能够较好地计算材料的迟滞特性,从而描述材料力学行为的时间相关性。
因此,数学模型在超弹性和粘弹性力学行为的模拟上效果较好,能够较准确地计算出具有非线性性、速率相关性和迟滞特性的应力-应变曲线,结果符试验规律,可以进一步用于其他结构件的动态特性的计算。
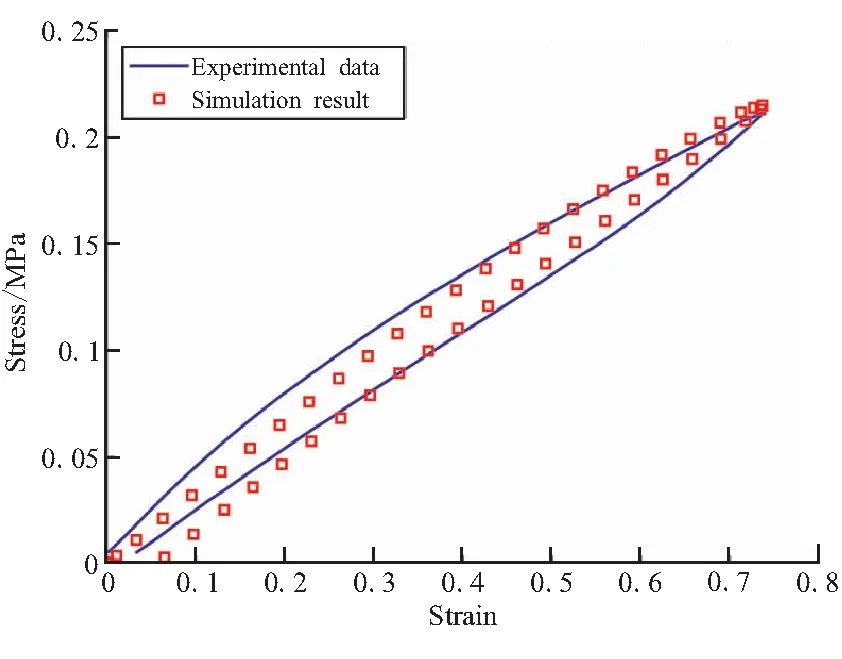
图15 四板剪切循环加载试验与仿真结果Fig.15 Result of test and simulation in 4-slicecycle loading process
4.3 数值研究
4.3.1 加载条件对计算结果影响
针对不同加载速率和不同应变水平的情况进行剪切循环的计算。
图16为70%应变水平下以速率240 mm/min和420 mm/min循环加载的计算结果对比,图17为以240 mm/min速率分别加载到应变为70%和110%的循环加载计算结果对比。
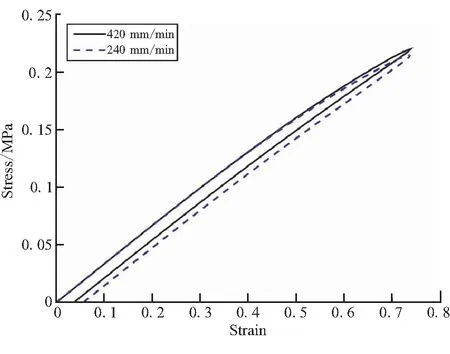
图16 应变水平70%不同加载速率的循环加载计算结果Fig.16 Result of cycle loading simulation with 70%strain at different rates of loading
最大应变水平一定的情况下,随着加载速度的增加,迟滞曲线的面积略有减小,加载到相同应变处所对应的应力略有增大;加载速率一定的情况下,最大应变水平迟滞环面积影响较大,即应变水平增大,循环过程能量损耗显著增加,主要是由于回复过程中载荷力减小造成的。因此,模型能够反映橡胶的动态迟滞行为及其在不同应变速率和不同应变水平下的变化规律。

图17 加载速率240 mm/min时不同应变水平的循环加载计算结果Fig.17 Result of cycle loading simulation at 240 mm/minloading rate with different strain levels
4.3.2 材料参数对模型的影响
Bergström-Boyce迟滞模型的材料参数需要通过不同速率下的试验数据进行辨识,但是由于这几个材料参数之间的耦合特性,确定所研究橡胶的粘弹性参数比较困难。参数和参数与高聚物分子的类型有关,与填充物无关;而参数和参数对模型影响较大。为了研究等效弹性伸长率和蠕变参数对模型计算迟滞特性的影响,以表3中参数为基础,分别改变和进行加载速率240 mm/min,应变70%的加载回复计算,结果如图18和图19所示。
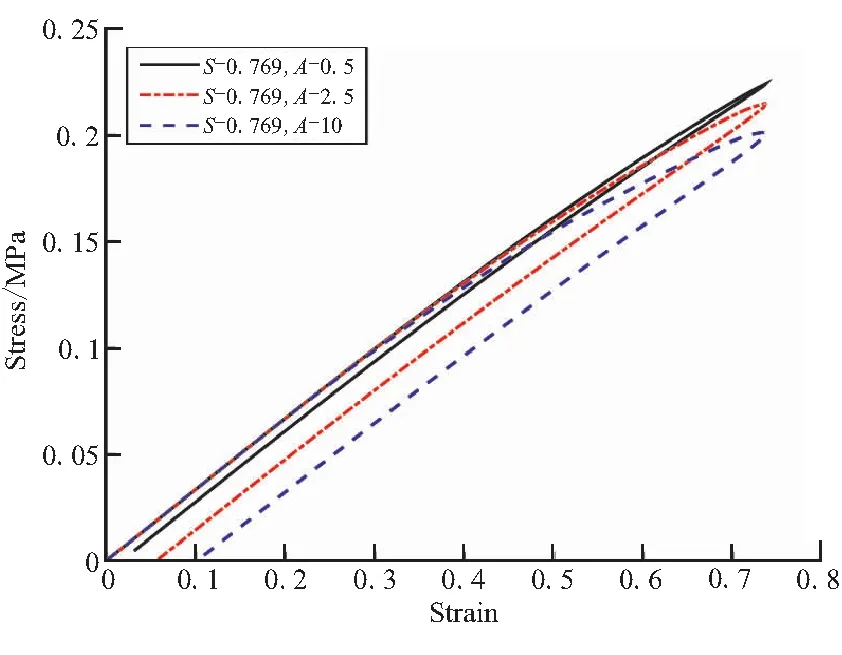
图18 改变参数A的迟滞计算结果Fig.18 Calculation results of hysteresis processunder changing parameter A
结果显示,增大参数,则迟滞曲线的包围面积增大,并且在应变较大的区域,更大的值使得应力值更小。这是因为在式(9)中,参数以比例形式改变等效蠕变速率,在越大的值下计算的等效蠕变速率也越大,分子链来不及松弛便发生了滑移使得滞后效应增强。相比之下,参数对迟滞计算的影响更为显著,参数增大,模型的迟滞特性也随之增强。参数是模型网络粘性部分(Network B)应力和弹性网络部分(Network A)应力的比例,因此增大时粘性部分的耗散也更大,当减小到图19中0.1的情况时,几乎体现不出迟滞效应,所采用的超-粘弹性模型便退化为只有A网络部分的超弹性模型。
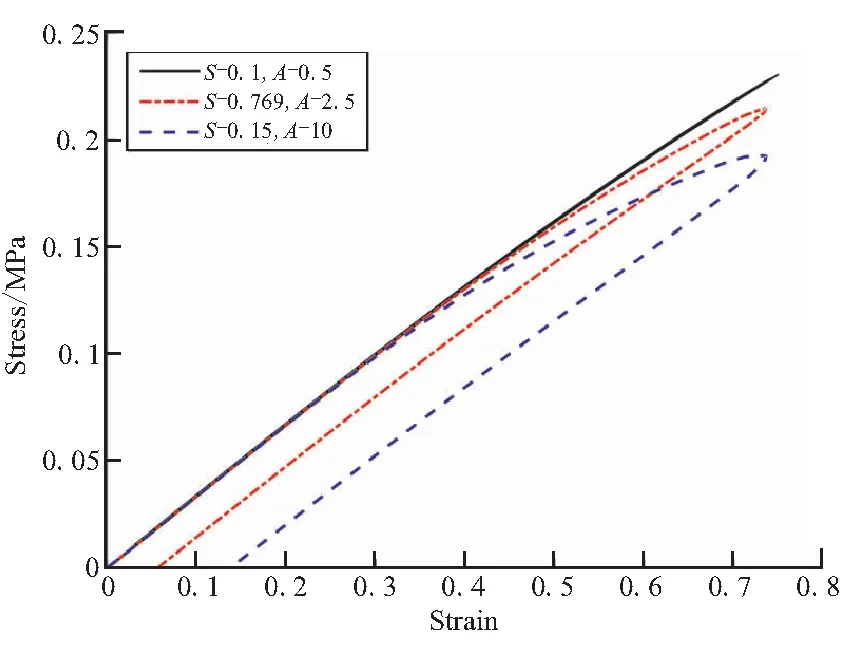
图19 改变参数S的迟滞计算结果Fig.19 Calculation results of hysteresis processunder changing parameter S
4 结论
(1)Mullins效应对四板剪切应力-应变曲线的影响比对单轴拉伸应力-应变曲线的影响更小,前者在第一次和第二次加载中应力值最大减少了50.6%,而后者应力值最大仅减少27.1%,另外四板剪切应力-应变曲线稳定较快,仅在两次加载之后的曲线就有较好的一致性。
(2)加载速率和应变水平对材料的迟滞特性都有影响;加载速率越大,应力值越大;应变水平增大,迟滞曲线面积显著增加,主要是由于回复段的加载力减小造成的。
(3)所使用的超-粘弹性模型,能够较准确地捕捉材料在单轴拉伸和剪切变形时的非线性、速率相关性和迟滞行为,计算不同速率剪切应力-应变曲线时最大误差不超过8%,而计算迟滞曲线时应力平均误差为9.80%,迟滞曲线包围面积计算误差为21.3%,并且对于不同的加载条件也能符合试验规律,在迟滞模型中,参数和的增大都能增加粘性的迟滞效应;以此为基础,可以指导柔性接头的动态计算建模。
杂志排行
固体火箭技术的其它文章
- 吸气式高速飞行器内外流耦合设计与多学科设计优化
- 固体发动机挂机滑块与壳体连接结构优化①
- 基于卷积神经网络的固体火箭发动机内弹道参数辨识①
- 实测燃速处理误差对内弹道性能预示的影响分析①
- A novel energetic potassium salt of 2,3,5,6-tetranitro-4H,9H-dipyrazolo [1,5-a:5',1'-d][1,3,5]triazinane:Synthesis,crystal structure and performance①
- Formulation research on UV-curable polyether modified HTPB solid propellant for 3D printing①
