基于三维八节点内聚单元的固体火箭发动机粘接界面结构分析①

崔辉如，王佳奇，吕 轩，许玉荣

(1.陆军工程大学 国防工程学院, 南京 210007；2.中国酒泉卫星发射中心，酒泉 732750；3.航天动力先进技术湖北省重点实验室，湖北航天技术研究院总体设计所，武汉 430040)

0 引言

固体火箭发动机作为性能优越的动力装置被广泛地应用于军事和航天等领域。高体分比、服役周期长以及竖直贮存等一系列的严格指标使得发动机粘接界面面临着前所未有的考验。

在粘接界面的监检测方面，不少科研人员开始利用红外热扫描和成像法进行绝热层/推进剂粘接界面的检测。海军航空大学在国内率先开展了固体火箭发动机界面实时监测系统设计与试验相关工作。通过将传感器埋入粘接界面处，并进行了长时间的跟踪监测。监测结果表明，传感器对界面的粘接性能影响较小，监测结果准确可靠。类似地，美国的空军实验室在绝热层与推进剂之间内置一定数量的传感器实时监测界面处的径向应力以及温度。

传统的仿真分析过程中，将粘接界面等效处理的方法已经难以满足现阶段界面破坏过程模拟的需求。在BARENBLATT和DUGDALE提出内聚力模型的概念之后，内聚力模型俨然成为描述脱粘过程强大的分析和数值计算工具。不少研究人员针对发动机粘接脱粘问题，利用内聚力模型开展了一系列的研究。CUI等通过建立松弛内聚力和松弛参数的方法，分别创建了两种粘弹性内聚力本构模型。仿真结果表明，这两类模型可以很好地应用于推进剂和绝热层之间粘接界面的分离破坏。马晓琳等通过内聚单元构建了衬层和推进剂粘接界面的二维有限元模型，通过反演手段获得内聚力模型参数，研究了发动机在典型工况下，推进剂和绝热层粘接界面的力学响应。南京理工大学团队采用内聚单元和双线性内聚力模型，在有限元方法的基础上分别开展了推进剂和绝热层粘接界面的I型、II型界面分离特性研究，并取得了一系列的成果。

综上可知，目前利用内聚力模型进行的界面力学行为模拟主要还集中在试验件层面。为了满足发动机粘接界面的结构完整性分析，本文从界面的力学模型入手，构建了三维八节点内聚单元，推导了单元内力矢量以及单元刚度阵，研究和建立有效的有限元仿真方法，并对某固体火箭发动机固化降温和点火增压两种工况条件下的粘接界面结构进行了三维有限元分析。

1 基于松弛效应的粘弹性内聚力本构模型

1.1 PPR内聚力本构模型

PPR内聚力模型是考虑物理断裂参数以及连续断裂边界的势相关内聚力模型。利用势函数与内聚力之间的关系，可以得到两个方向的内聚力表达式。

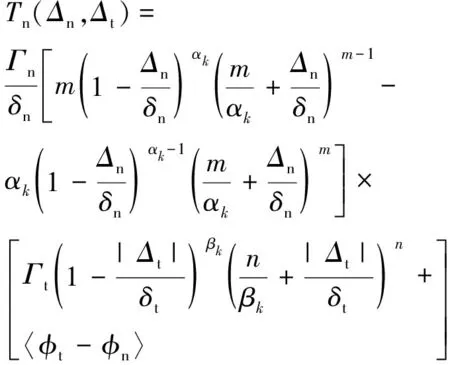
(1)

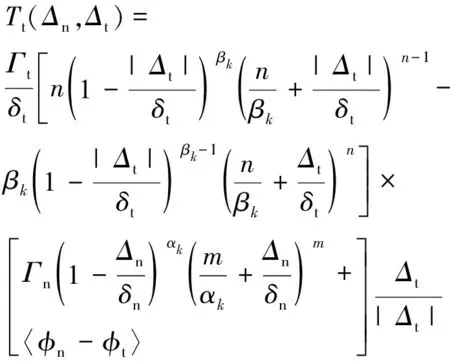
(2)

式中和分别代表法向和切向的分离位移；和分别代表切向和法向内聚能；和为能量常数；和为初始斜率参数；和为模型的形状参数，分别控制法向和切向的内聚力和分离位移曲线下降段的凹凸特性；和为模型的法向和切向的临界位移。

和的计算与两个方向的内聚能相关。

(1)当≠时

(3)

(2)当=时

(4)

此外

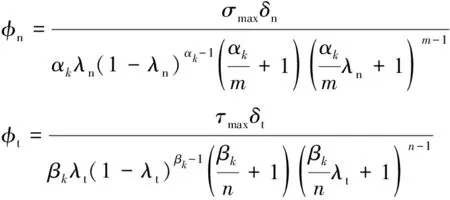
(5)

式中和为法向和切向内聚强度；和为初始斜率指针。

(6)

PPR内聚力模型的控制参数可以分成4组，即初始斜率参数、，内聚强度、，临界位移、以及形状参数、。

1.2 粘弹性内聚力模型

大部分的情况下，衬层内的粘接剂和固体推进剂的粘接剂采用相同的高聚物配方，是典型的粘弹性材料。研究表明，粘接界面具有典型的粘弹性效应。为此，CUI等提出了粘接界面内聚参数随时间松弛的假设：

(1)时间相关内聚力的内在机制是内聚力模型参数的松弛，这些内聚力模型参数包括临界位移、内聚强度以及初始斜率参数。

(2)时间相关的内聚力依然是内聚力模型中势函数对分离位移的偏导数，这一条件在任意时刻都满足。

(3)加载时间以及加载温度的力学效应可以依据时温等效原理进行相互转化。

根据上面的基本假设，这里采用形如()=+exp(-)的标准线性固体松弛模型。为了使得系数在初始时刻为1，那么+=1。初始的内聚力模型参数乘以松弛系数就可以获得松弛的内聚力模型参数。式(7)以I型内聚参数为例给出了松弛的临界位移、内聚强度以及初始斜率参数的时变关系：

(7)

式中(0<<1)、(0<<1)、(0<<1)、、以及为未知的松弛参数；(0)、(0)以及(0)为=0时刻的内聚强度、临界位移以及初始斜率参数。

考虑到加载温度的影响，依据时温等效原理获得的缩减时间将会被引入到以上定义之中，即

(8)

其中

(9)

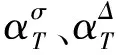
(10)

1.3 缩减时间的数值积分

本部分将具体介绍如何在增量步中计算松弛型的内聚力模型参数，主要的工作将集中在缩减时间的计算上面。接下来的部分将以内聚强度为例进行介绍。

如式(11)，缩减时间是温度的非线性函数。通过两边进行求导，可得

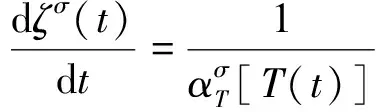
(11)

为了计算缩减时间，这里将采用增量的方法。将计算时间区间分解成份时间子区间，即

(12)

令

(13)

假设温度()以及()在时间区间[,+1]上线性变化，那么

()=+

(14)

其中

(15)

结合上式，可得

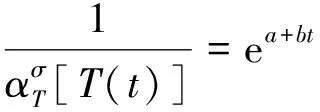
(16)

依据式(16)，缩减时间的增量可以表示为

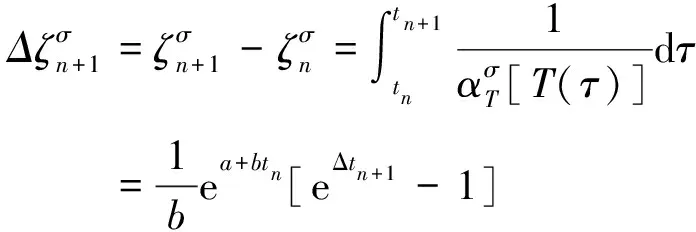
(17)

计算过程中，时间增量Δ+1是已知量，与之对应的临界位移，内聚强度以及初始斜率参数的缩减时间可以采用以上方法获得。

2 三维八节点内聚单元

为了实现对粘弹性内聚力本构模型的应用，还需要开发相应的内聚单元。目前，为了确保有限元分析精度，三维固体火箭发动机结构完整性分析大都采用六面体单元。相应地，内聚单元主要采用三维八节点的形式。为了简化问题，这里仅讨论初始厚度为0的三维八节点内聚单元，如图1所示。

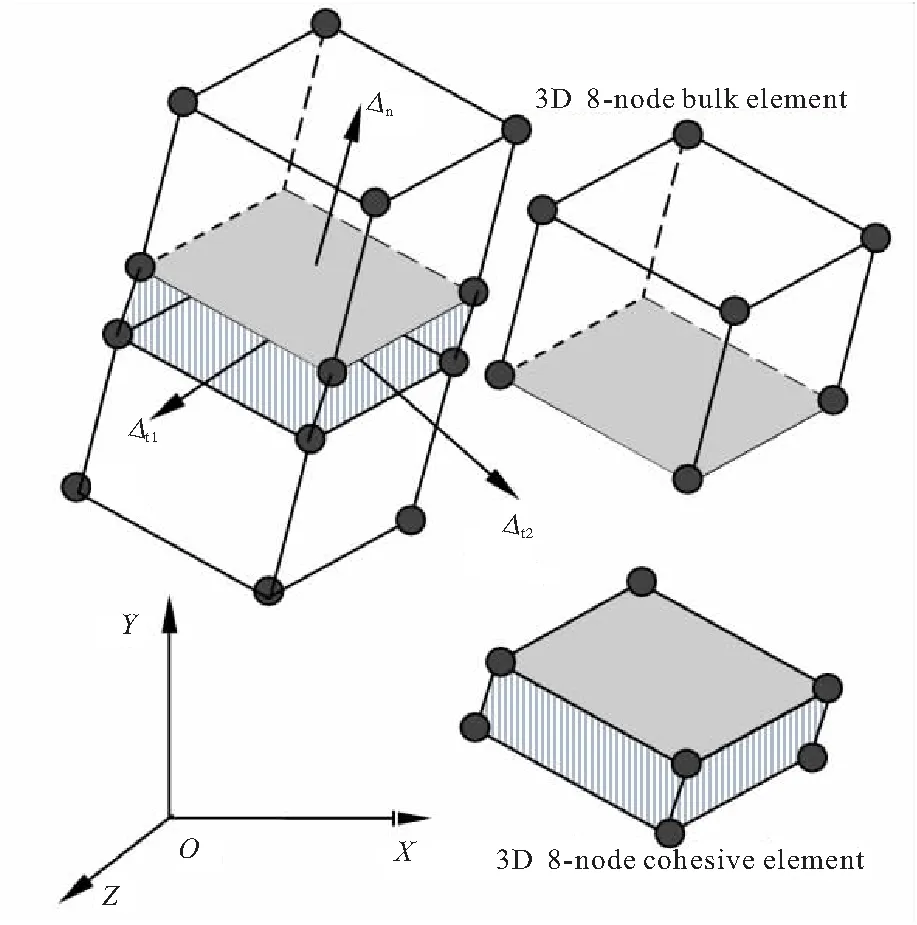
图1 三维八节点零厚度内聚单元应用示意图Fig.1 Application diagram of 3D 8-node zero-thickness cohesive element

2.1 单元位移变换矩阵推导

在进行三维八节点内聚单元的推导之前，需要对单元的编号规则进行简单的介绍。如图2所示，单元的下表面的节点编号按照逆时针的规则分别为节点1、2、3、4。与之对应的单元的上表面的节点编号按照逆时针的规则分别为节点5、6、7、8。首先提取三维内聚单元的中面，即平面1′2′3′4′。

如图3所示，规定为单元所处的整体坐标系，为单元参考的坐标系。假设中面各顶点的坐标在整体坐标系和参考坐标中分别表示为

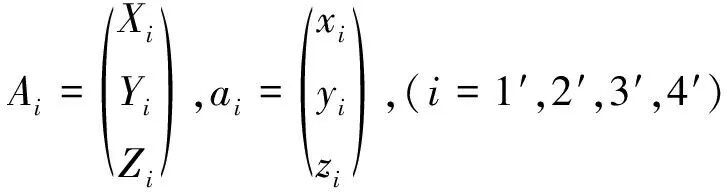
(18)

依据中面的定义，顶点1′、2′、3′、4′的整体坐标可表示为式(19)～式(22)。

图2 三维八节点内聚单元及其中面示意图Fig.2 Diagram of 3D 8-node cohesive element and its middle surface

图3 三维八节点内聚单元参考坐标系示意图Fig.3 Reference frame scheme for 3D 8-node cohesive element

(19)

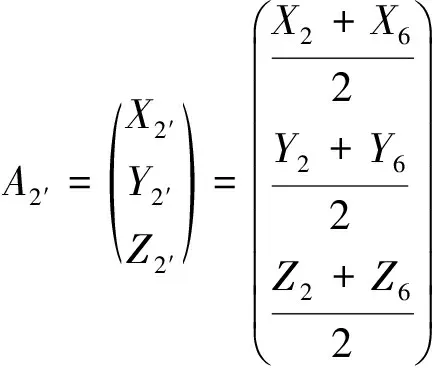
(20)

(21)

(22)

参考坐标系的原点可以选择在单元内的任意一点，以1′点为例，即

=

(23)

在单元平面内选择和轴，那么轴自然垂直于单元面，按照角点1′→2′→3′右螺旋指向的正方向。

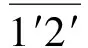
(24)

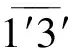
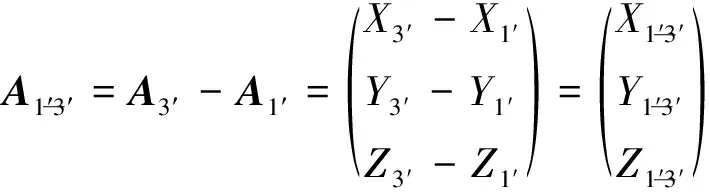
(25)

那么，轴的方向余弦为

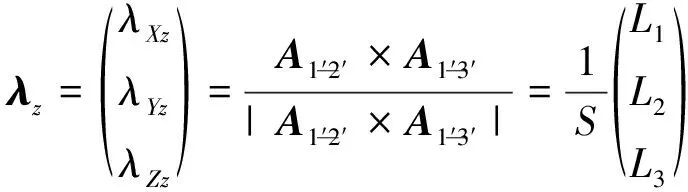
(26)

其中

(27)

(28)

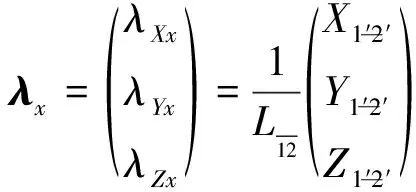
(29)

其中

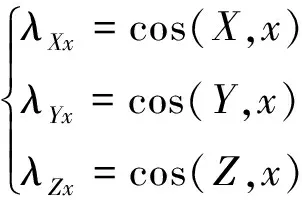
(30)

(31)

此时，方向的余弦可以由轴和轴确定，根据右螺旋法则有

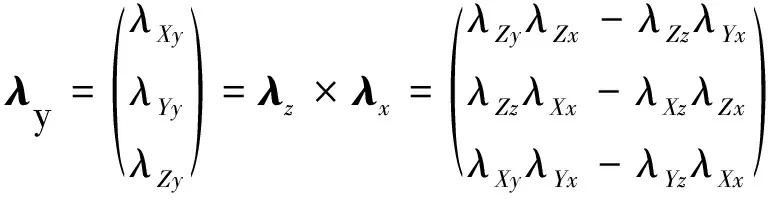
(32)

坐标变换矩阵为

(33)

以上图为例，参考坐标系内的节点位移向量为

(34)

总体坐标系内的节点位移向量为

=[]，(=1,2,…,8)

(35)

节点的位移向量满足

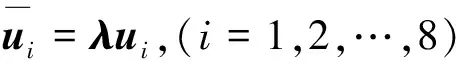
(36)

为方便，令

=[]

(37)

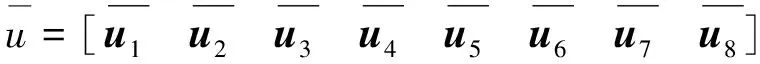
(38)

单元的节点位移向量满足

(39)

(40)

式中代表三阶单位矩阵。

2.2 单元分离位移场推导

已知内聚单元变形后节点的参考坐标表示为

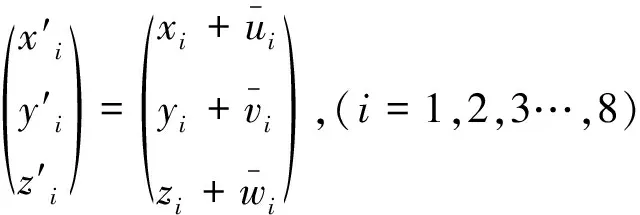
(41)

那么，参考坐标系下的分离位移为

=[]，(=1,2,3,4)

(42)

(43)

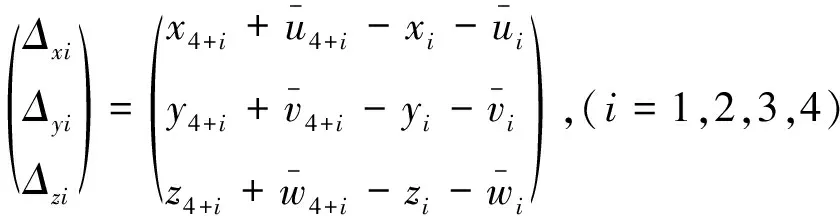
(44)

考虑到零厚度单元：

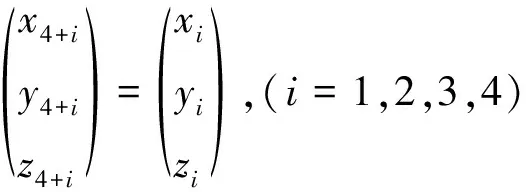
(45)

(46)

=[]

(47)

建立节点分离位移与节点参考位移间的关系

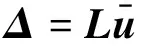
(48)

其中

=[-]

(49)

建立分离位移场与节点分离位移关系：

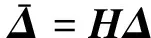
(50)

其中

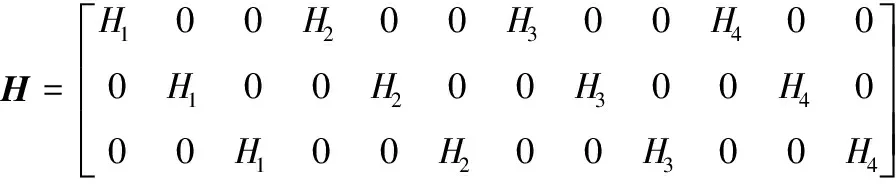
(51)

(52)

建立分离位移场与节点整体位移间的关系，即

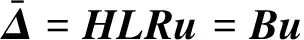
(53)

2.3 八节点六面体等参单元

类似四边形的等参元，可以建立八节点六面体等参单元。对于如图4所示的等参单元，其形函数在自然坐标系中如式(54)所示。

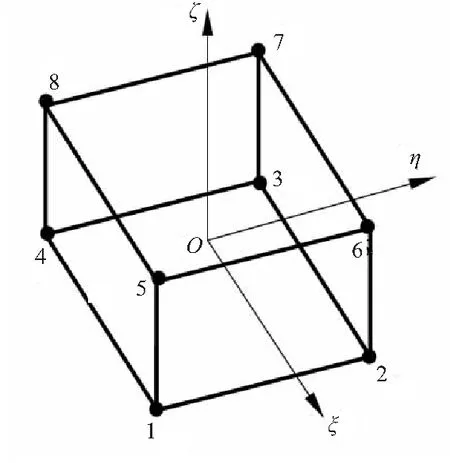
图4 自然坐标系中的八节点六面体等参单元Fig.4 8-node hexahedral isoparametric element in natural coordinate system

(54)

类似地，可以通过形函数，建立自然坐标系中的点与图5中物理坐标系中的点之间的映射关系，即

(55)

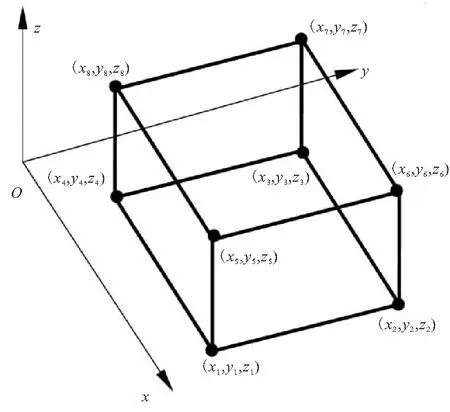
图5 物理坐标系中的八节点六面体单元Fig.5 8-node hexahedron element in physical coordinate system

对于单元上的面积积分而言，令

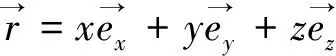
(56)

(57)

利用自然坐标系有

(58)

中面上(=0)的面积积分为

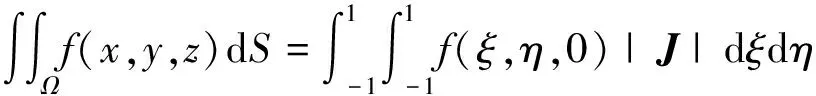
(59)

(60)

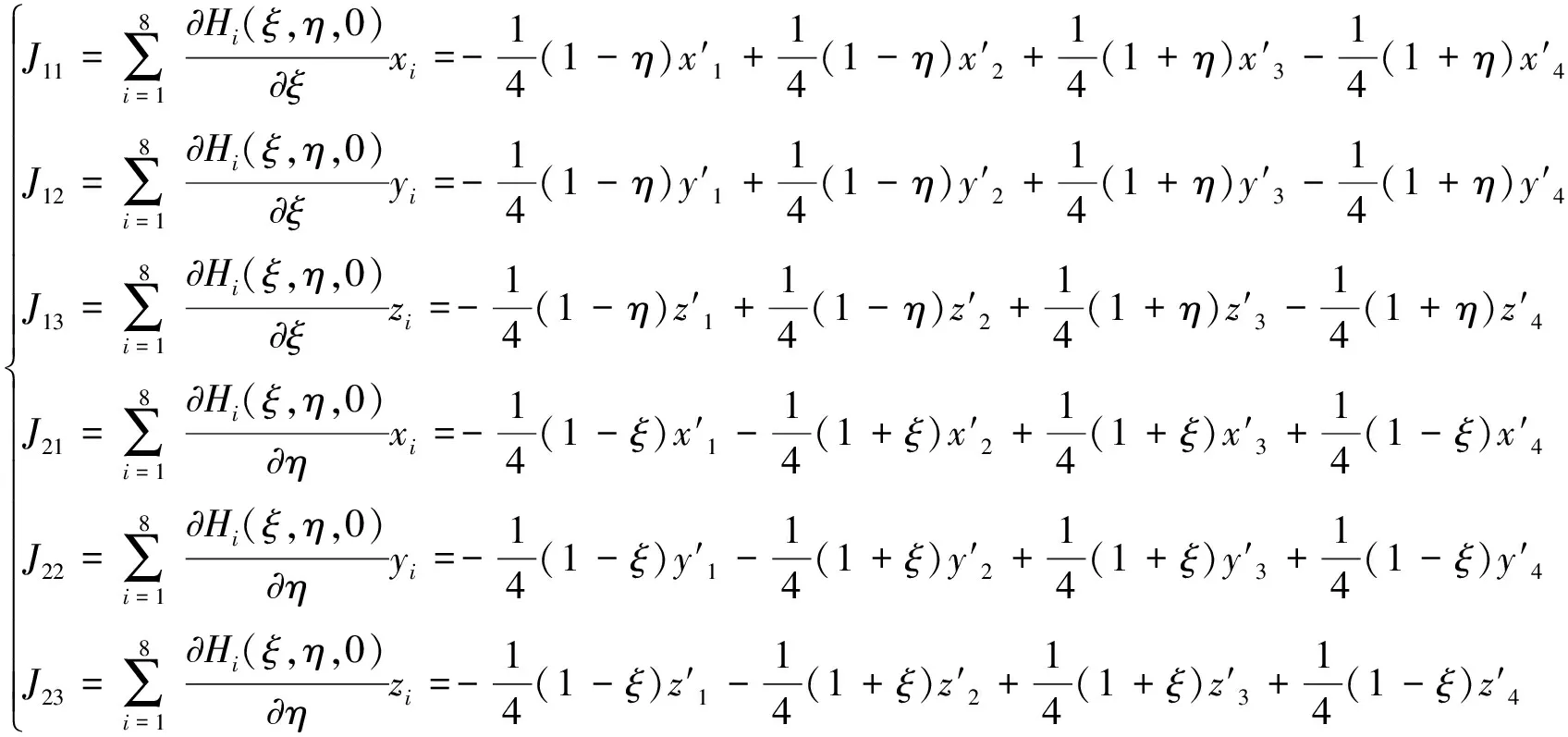
(61)

故

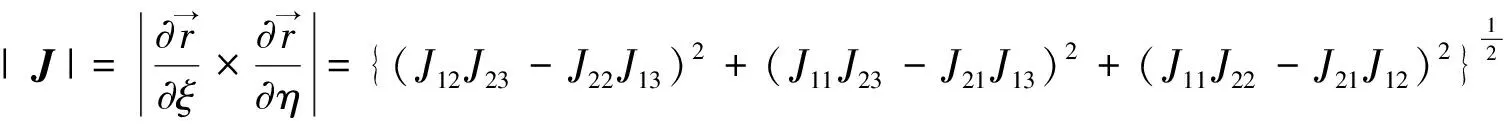
(62)

2.4 单元内力矢量及单元刚度阵推导

依据虚位移原理，有

(63)

式中和分别为格林应变张量和第二PK应力张量；和分别为分离位移及内聚力；为单元中面；、分别为外力及节点位移矢量；为整个单元外边界。

通过伽辽金法结合等参元理论，推导可得单元的刚度矩阵及内力矢量为：

(64)

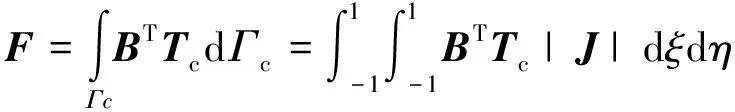
(65)

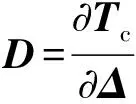
基于以上推导并结合ABAQUS中的用户单元模块，将本文开发的内聚单元进行有限元应用。

2.5 单元验证算例

验证算例的主要对象为弹性圆管粘接结构，如图6所示。圆管的内外径分别为8 mm和2 mm。在圆管靠近外表面的位置，沿着圆管的径向，设计了长度为3 mm的预制裂纹。圆管的内部受压，压力值为1 MPa，圆管结构的底部被固定约束。沿着预制裂纹的方向是后加工而成的粘接界面，结构受内压过程中，裂纹将沿着粘接界面的方向扩展。材料的杨氏模量以及泊松比分别为10 MPa和0.33。PPR模型的初始参数满足(0)=0.5 MPa，(0)=0.1672，=3.10以及(0)=2.5 mm。另外，切向的内聚参数假设和法向是一致的。

图6 圆管结构几何模型(单位：mm)Fig.6 Geometrical model of tubular structure (unit:mm)

为了方便分析粘弹性模型的特性，这里定义模型的参数满足

====03

====50

(66)

网格方面，图7针对圆管结构本文分别采用了二维四节点单元(Q4)和三维八节点单元(Hex8)。网格主要的尺寸为0.5 mm，三维网格结构的整体厚度为2 mm。这里的二维单元均采用平面应力单元。网格规模上，六面体网格的数量是四边形网格数量的4倍。在结构的粘接界面处分别设置了经过文献[31]检验的二维四节点内聚单元(COH2D4)和本文设计的三维八节点内聚单元(COH3D8)。内聚单元数量方面，六面体网格中的内力单元是四边形网格中内聚单元数量的16倍。

(a)Quadrilateral mesh

(b)Hexahedral mesh图7 圆管结构网格Fig.7 Mesh for tubular structure

图8给出的是不考虑温度变化条件下，内压在8 s内从0 MPa匀速增加到0.8 MPa时，圆管结构顶部裂缝宽度随时间的变化。可以发现，不同网格在平面应力下的计算结果和三维应力状态下的计算结果是对应一致的。通过以上分析，可以认为，本文提出的内聚单元推导过程和仿真方法是准确的。

图8 裂缝宽度随时间分布曲线Fig.8 Crack width versus time

3 粘接界面结构完整性分析

3.1 发动机有限元模型

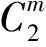
表1 推进剂松弛模量Prony级数系数

表2 粘弹性粘接界面内聚力模型参数

如图9所示，在发动机推进剂和绝热层之间对网格进行加密，尽量将内聚单元附近的网格质量对结构分析的影响降到最低。在提交计算时，根据对称特性，对结构的环向位移进行约束。为了抑制刚体位移，对发动机壳体的一端进行约束。

(a)Overall schematic diagram

(b)Partial grid diagram between propellant and insulation(case,insulation and propellant from outside to inside)图9 发动机有限元网格示意图Fig.9 Finite element mesh diagram of solid rocket motor

3.2 固化降温分析

药柱在零应力温度58 ℃(331.15 K)浇注成型，还需要经过长达1 d(86 400 s)的固化降温阶段，直到温度降到室温20 ℃(293.15 K)。在这一阶段，假设发动机结构内部是没有温度差的。发动机内部的温度变化曲线可以近似表示为

()=-(-)×(1-e- ×10)

(67)

其中，为初始固化温度；为室温；参数=8 s；时间以秒计。

固化降温的初期，温度变化较快，在降温的后半段时期，温度变化较慢。固化降温结束时，推进剂和绝热层粘接界面上的内聚力分布云图如图10所示。可以发现，在粘接界面的两端，单元的切向和法向内聚力急剧增加。在降温阶段，药柱热胀系数较大，药柱整体向中心收缩。因此，药柱两端的变形剧增，这就导致了粘接界面在两端的内聚力较中间部位稍大。从发动机的纵剖面，更加直观地表现出了这一趋势。

此外，从图10(a)可以看到，切向内聚力(这里的切向内聚力是发动机纵向和环向内聚力的合力)在发动机的纵向会出现明显的极小值，这一极小值在圆管段区域。法向内聚力方面，如图10(b)所示，由于推进剂沿着法向的装填量有一定差异，降温时收缩变形量不同，法向内聚力在星孔段以及翼槽段会出现一定的波动，而在圆管段，法向内聚力基本保持不变。

在固化降温结束时，粘接界面上最大的切向和法向内聚力分别为0.03 MPa和0.065 MPa，远小于粘接界面的内聚强度，此阶段粘接界面结构破坏的可能性较低。

(a)Tangential direction (b)Normal direction图10 固化降温结束粘接界面内聚力空间分布云图Fig.10 Spatial distribution of traction on the bonding interface at the end of cooling stage

3.3 点火增压分析

发动机的点火增压阶段是发动机结构设计中另一个较为危险的阶段。为了方便计算，这里直接给出发动机点火建压过程中的-关系式：

()=(1-e-)

(68)

其中，=6 MPa为内压峰值；时间的单位为s；参数=20 s；这里加压时间采用0.3 s。

图11给出了三维发动机结构在20 ℃状态下点火增压结束时，发动机推进剂和绝热层粘接界面上的法向和切向内聚力分布。与固化降温阶段不同的是，在点火增压阶段，药柱的侧面也是受到燃气压力作用的。因此，在增压阶段，切向内聚力并没有在界面的两端出现极值。在点火结束时，粘接界面上最大的切向和法向内聚力分别为0.11 MPa和-0.348 MPa。此外，云图结果显示，粘接界面上不存在界面单元失效情况，点火增压结束时，粘接界面结构安全。

图12给出了发动机粘接界面上靠近模型边界处的三个特征点上切向和法向内聚力随时间的分布。其中，点位于圆管段的端部，点位于翼槽段的中间部位，点位于星孔段的端部。可以看到，随着点火阶段的推进，内压逐渐增大，粘接界面上的切向和法向内聚力都将逐渐变大。此外，由于空间位置的不同，切向内聚力方面差异较大，但是法向内聚力的差异较小，这与该阶段处于受压状态有关。

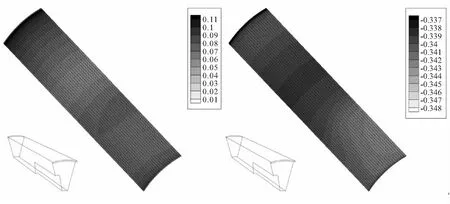
(a)Tangential direction (b)Normal direction图11 点火增压结束粘接界面内聚力空间分布云图Fig.11 Spatial distribution of traction on the bonding interface at the end of ignition pressurization stage

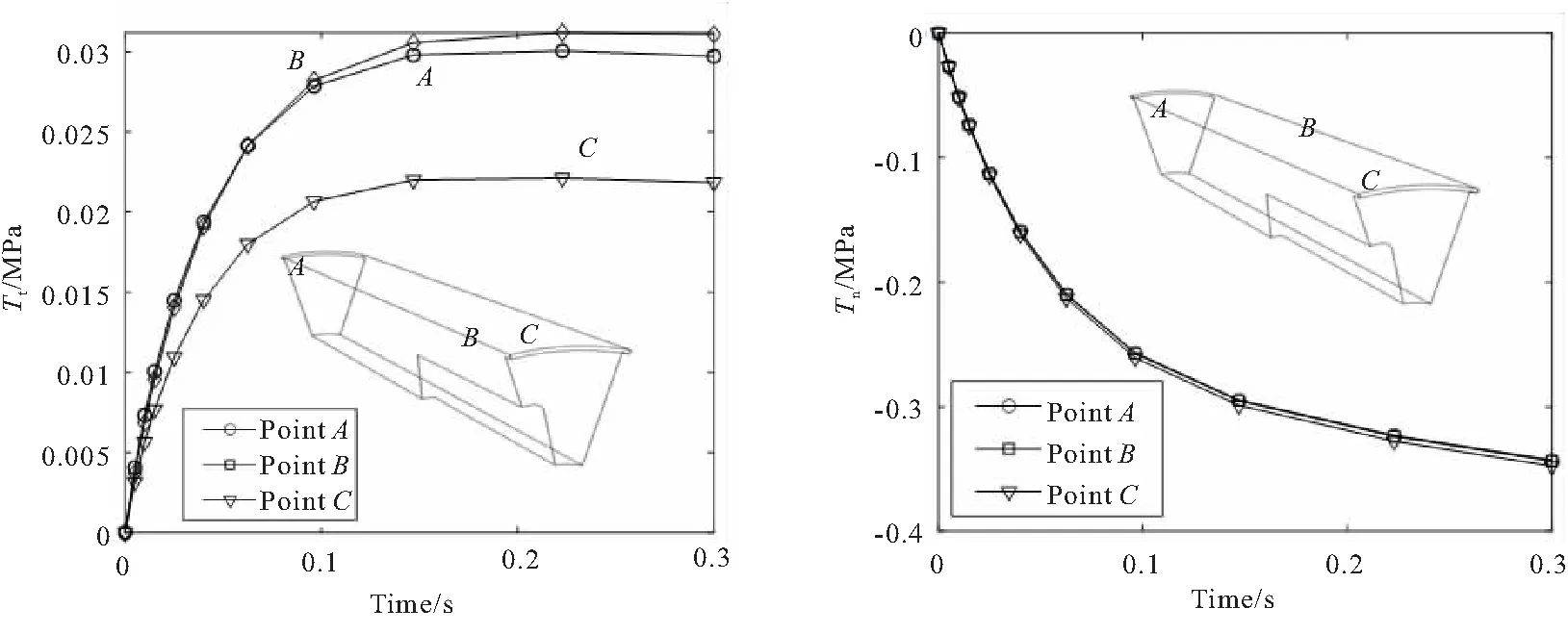
(a)Tangential direction (b)Normal direction图12 点火增压阶段粘接界面内聚力随时间变化曲线Fig.12 Traction on bonding interface versus time during ignition pressurization stage

4 结论

(1)通过圆管粘接结构中的裂纹扩展算例，验证料三维八节点内聚单元，建立了含粘接界面复合结构的有限元仿真计算方法。相比于传统的结构分析手段，该方法可以通过内聚单元直接获得推进剂与绝热层粘接界面上内聚力的分布，为粘接界面的结构完整性分析提供判断依据。

(2)针对某发动机固化降温和点火增压工况，开展了三维发动机粘接界面的有限元仿真分析，得到如下结论：

1)在固化阶段，由于被粘接材料热胀系数的差异，推进剂收缩的速率明显比绝热层高，粘接界面受到持续的分离效应。固化降温结束时，粘接界面上最大的切向和法向内聚力分别为0.03 MPa和0.065 MPa，远小于粘接界面的内聚强度。

2)在点火增压阶段，粘接界面的法向持续受压，界面的法向比较安全。但是由于持续的挤压，界面两侧的切向位移不连续加剧，导致界面的切向内聚力增加明显，相比于固化降温结束阶段，增加了近2.7倍。点火结束时，粘接界面上最大的切向和法向内聚力分别为0.11 MPa和-0.348 MPa，不存在界面单元失效情况，粘接界面结构安全。