基于迁移学习的卷积神经网络的金融指数预测

李子玥 曲英伟

（大连交通大学 软件工程学院 辽宁省大连市 116028）

1 引言

与传统的金融指数相比，互联网金融指数起步较晚，其原因在于互联网金融的起源比较晚。国外的相关研究资料较少，国外提出一种电子金融，类似于我们国内所研究的互联网金融。这是因为国外的发达国家的金融业发展较早，当互联网技术成熟更新后，他们已经形成了稳定的能经受考验的金融市场体系。而我们国家互联网金融起源于20 世纪末到21 世纪初期，在招商银行开通了招商银行的官网，标志着我们国家金融电子服务进入了一个网络时代。随着电子商务的兴起，我们国家的互联网时代进入了一个新的阶段，此时我们可以借助于手机查看各种的金融理财产品。当大量的互联网企业开始涌入市场时，互联网金融也进入了一个高速发展阶段并逐步趋向于成熟。简单来讲互联网金融就是基于互联网技术和互联网环境而进行的一个金融活动，是一种新的金融模式。互联网金融指数就是基于与金融相关的互联网上市公司或关联上市公司编制而得的股票指数。

迁移学习理论最早是Thorndike 和Woodworth 在1901年从心理教育学的角度提出，后来随着机器学习的发展，人们猜想机器能否像人一样进行学习的迁移，在学习已有的知识内容上能够很快的学会相类似的知识内容。在1995 年NIPS-95 的“学会学习(learning to learn)”的专题研讨会上正式开始对迁移学习的研究。能够进行迁移学习的内容可以分为两部分，把已知的知识内容或者是带有标签的数据记为源域或者是源任务，把想要进行学习的新内容或者是没有标注标签的数据记为目标域或者是源任务，找到源域与目标域之间的共性进行学习，从而完成目标域任务。迁移学习常用来解决数据量较少或者是个性化的问题。

1998 年纽约大学的Yann Lecun 首次提出局部连接和权值共享的方式的卷积神经网络，该算法不仅减小了过拟合现象而且利用共享权值使网络因权值量减少而优化。卷积神经网络可以按照输入信息的结构进行平移不变的分类，同时是一种有深度结构和卷积计算的前反馈神经网络，因此也称为“平移不变人工神经网络”。卷积神经网络对输入的数据进行处理，通过特征提取进行局部特征提取，特征与其所在空间位置确定；通过特征映射结构中的激活函数使特征映射具有位移不变性，这些工作主要在卷积层完成。池化层进行信息的筛选和过滤，全连接层将提取的特征进行非线性组合，输出层采用逻辑函数或归一化函数进行分类输出。更详细分析整个卷积过程即分析这几层的运算过程：

（1）卷积计算：能进行学习的卷积核与前面的特征图卷积后经激活函数形成本层特征图；

（2）池化运算：该步骤即把上层特征图分割不重叠的区域进行池化降低网络空间分辨率，可以消除信号的偏移，常见的方式有最大池化层、均值池化层和随机池化层。

（3）全连接运算：将多组信号依次组合为一组信号。

（4）识别运算（输出）：经过前面的特征学习运算，根据实际需要加上一层进行分类输出。

卷积神经网络属于神经网络的一种，具有多层网络结构，同时还具有权值共享、局部连接、池化操作。一般是由输入层、卷积层、池化层、全连接层和输出层构成。输入层的神经元个数取决于输入的特征个数，卷积层和池化层对特征进行再次提取同时池化层具有降噪的作用，全连接层的输出值传给输出层，根据输出的结果的要求可以选择逻辑回归函数进行分类。经典的CNN 结构是卷积层和池化层进行交替连接最后通过一个或者是多个全连接层输出。卷积神经网络的不同结构所应用的场景不同，对于时间序列分析或者是对自然语言的处理常采用一维的结构，对输入数据进行调整为一维矩阵；二维结构则用于日常所见的图片处理，计算机视觉处理，数据输入是常规矩阵形式；三维结构更多用于医学上的ct影响，或者是摄像头对工作环境中的人物识别检测，比如常见的火车站的人物是否戴口罩，回放视频中人物是否佩戴安全帽等。在做实验中，如何选取合适的卷积神经网络结构则需要看实验研究领域进行确定，也可以重新搭建合适的结构层次。

随着人工智能、机器学习的发展，借助于BP、LSTM、RNN 等神经网络对金融指数的趋势走向研究越来越多，近年来CNN 的研究发展也让学者把目光放在对金融时序问题的研究上，并且取得较好的结果。本文是基于python 库中的卷积神经网络对传统金融指数的价格趋势进行模型预训练，同时在获得预训练模型的基础上进行迁移学习得到新的模型进行数据量较少的互联网金融指数的预测，预测效果比用CNN 单一模型较好。

2 文献综述

从互联网金融概念的提出后，不少学者对其进行了不同方面的研究。李烨（2014）从互联网金融的定义、分类和发展进行分析构建互联网金融指数指标体系的理论依据。黄锐、黄剑（2016）基于98 家商业银行的面板数据证明互联网金融给传统的金融带来了竞争，提高了风险但也提高了盈利能力。申创、赵树敏（2017）基于101 家商业银行首次利用百度指数构建的互联网金融指数，理论加实证分析的方法分析了互联网金融对商业银行收益的影响。戴天骄（2018）利用Realized EGARCH 模型和时变Copula 模型分析发现互联网金融行业和金融行业的股票指数有明显的尾部相关性。多层前馈神经网络的CNN 在金融指数价格趋势的应用也有一定的发展，部分研究利用k 线图进行特征分析还有一部分是通过转换金融数据的维度进行分析预测。王希峰（2017）进行了基于卷积神经网络的K 线图有效性的验证。孙舒蓉（2020）通过构建新的卷积网络结构验证K 线图以图片的形式能够被卷积神经网络识别并分类预测。陈祥一（2017）利用卷积神经网络强大的监督功能以及从不同的角度进行模型调优使得模型在对股票指数未来一分钟和五分钟的价格趋势变动中取得了较高的预测结果。章静怡（2020）构建的引入平均趋向指标ADX 卷积神经网络模型在股票指数价格趋势预测中取得较好的结果。迁移学习与卷积神经网络结合模型在各个应用领域也有一定的进展。杨子文（2019）针对传统抽象图像情感识别任务中“语义鸿沟”的问题和数据集小样本问题提出一种基于两层迁移卷积神经网络的抽象图像情感识别模型。徐旭东、马立乾（2018）通过经典的卷积神经网络VGG16 和迁移学习在相同样本的条件下提高了控制图识别的准确度。陈立福、武鸿（2018）等人针对卷积神经网络中因网络参数随机初始化和参数过多导致的收敛速度慢及过拟合的问题，提出了一种基于迁移学习监督式预训练的卷积神经网络。所以，利用卷积神经网络特征提取的优势以及迁移学习解决小样本容量问题对于解决当前数据量较少的互联网金融指数预测准确度具有一定的可行性。

3 预训练模型构建及测试

3.1 预训练模型构建

卷积神经网络的卷积层，池化层全连接层又称为隐藏层，总体划分卷积神经网络的架构即为三大层，输入层，隐含层和输出层。卷积神经网络的一维卷积更适合用于时序序列的数据，因此本次实验采用一维卷积网络结构，由单个神经元构成输入层连接卷积层和池化层进行数据处理再通过输入层输出。同层神经元之间相互独立，不同层之间的神经元相互连接。一维卷积神经的卷积核可以看做是一个向量在一个方向上进行移动，对于时序数据就是在时间列上进行移动，样本中的一个数据所拥有的特征可以看成是该数据的多个维度，可以类比对文本数据的分析。

按照金融数据的日数据，输入最高价、最低价、开盘价、收盘价以及成交量，在卷积层和池化层进行特征提取之后进行平坦化连接全连接层进行输出。设置滤波器大小为64，卷积核大小为2，步长为1，激活函数使用常用的Relu 函数。Relu 函数输入值小于0 时输出值为0，输入值大于0 时输出值等于输入值，且在反向传播中减轻梯度弥散在正向传播中可加快传播速度。池化层使用最大池化层，池化大小为2，以前一天的涨跌预测第二天的涨跌趋势。为防止数据过拟合加入Dropout 层，参数设置为0.5。Dropout 层会随机地为网络中的神经元赋值零权重。参数设置为0.5 表示有一半的神经元将是零权重，降低对数据微小变化敏感度，提高对不可见数据的准确度。损失函数用来描述真实值与预测值的不同程度，常用来衡量模型的性能，本实验选择的平均绝对函数是通过计算真实值与预测值差的绝对值来衡量模型。

步骤一：通过财经网站和软件获取实验日数据和对应的研究的五大指标，并进行实验数据的处理，剔除掉数据残缺的样本；

步骤二：将预处理后的训练集数据以一维日频形式输入模型中进行训练；

步骤三：将预处理后的预测集数据以一维日频形式输入训练后的模型中，将结果与真实值进行比对；

步骤四：利用平均绝对函数作为损失函数进行估测与真实值的误差。

3.2 数据集确定及预处理

实验数据选用标准普尔500、恒生指数均从2000 年一月到2010 年十二月共十年的数据；互联网金融数据选取2015年一月到2020 年12 月共五年的数据。经分析之后选取实验数据不存在残缺样本。

将当天的收盘价作为此时的预测标签以此来应用监督学习序列，对输入的数据指标按照日期形式转换为整数编码。

3.3 模型预训练及测试

模型数据中，实验的前80%数据为训练数据，20%为预测数据。图1 为标准普尔500 训练集和测试集上损失函数值的下降情况，横坐标是轮次，纵坐标是损失函数值。

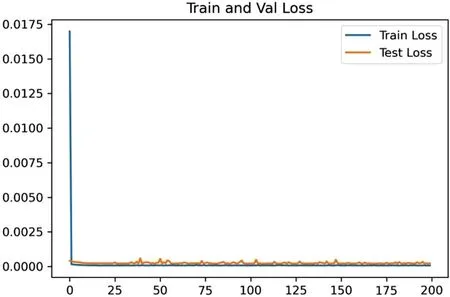
图1：标准普尔500 损失函数

标准普尔500 的真实值与预测值的平均绝对误差（MAPE）值为1.097%，损失函数值约在0.003，训练轮次约在10 左右达到稳定。

图2 为恒生训练集和测试集上损失函数值的下降情况。

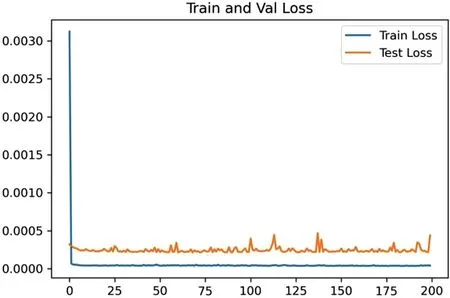
图2：恒生指数损失函数

恒生指数的真实值与预测值的平均绝对误差（MAPE）值为1.566%，损失函数值约在0.0035，训练轮次约在75 左右达到稳定

图3 为互联网金融指数训练集和测试集上损失函数值的下降情况。

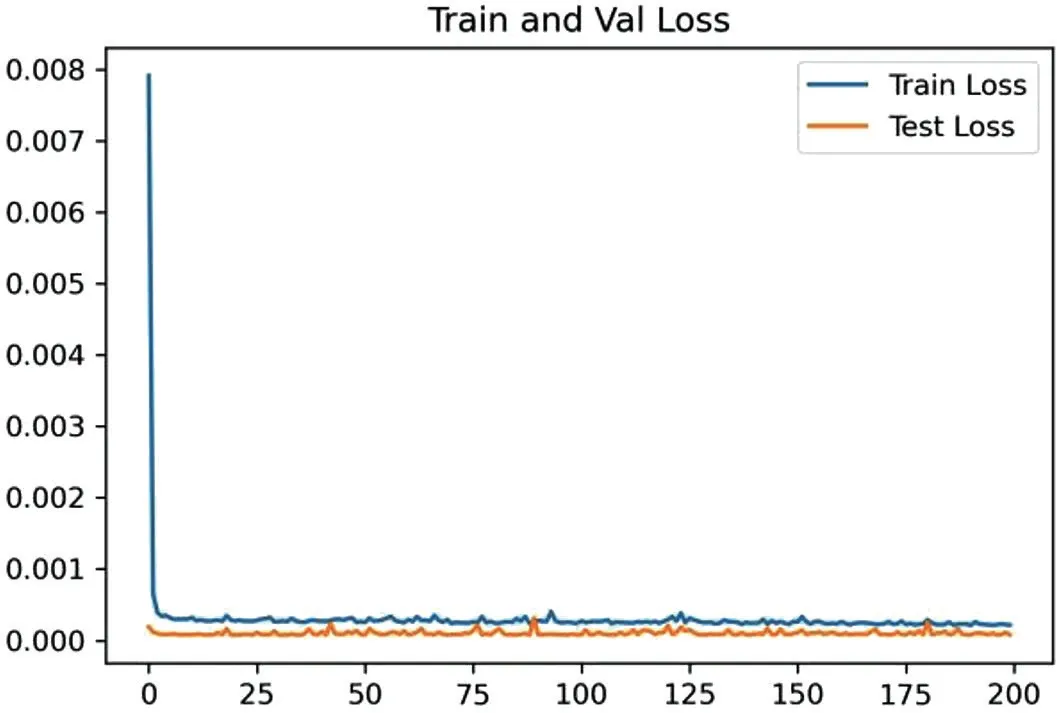
图3：互联网金融指数损失函数

互联网金融指数的真实值与预测值的平均绝对误差（MAPE）值为2.076%，损失函数值约在0.0002，训练轮次约在10 左右达到稳定。

经过实验结果对比，使用卷积神经网络构造的模型比使用LSTM 模型效果在整体上具有一定的优势。

4 基于迁移学习的金融指数预测

引言内容介绍了迁移学习本质上就是模仿人类在学习一定的内容知识后再次去学习新的相关内容的时候能更容易更快的接收，在机器学习中将算法先进行数据的训练形成一个学习好的模型，之后再该模型的基础上进行新的数据集的部分数据的训练作为新知识进行迁移学习，最后将进行迁移学习后的模型进行验证数据集的实验，并将实验结果与真实值进行比较，完成卷积神经网络的迁移学习。

实验步骤：

步骤一：获取标准普尔500，恒生指数在一维卷积神经网络算法下得到的预测模型一、二；

步骤二：将互联网金融指数数据进行预处理后分成训练集和验证集；

步骤三：将步骤二的训练集放入步骤一的到的预训练模型一和二进行迁移学习，得到学习后的新模型三和四；

步骤四：将互联网金融指数数据的验证集放入学习后的新模型中进行对比实验；

步骤五：分析实验结果得出结论，并用平均绝对函数进行误差估测。

使用前面的预训练模型进行迁移学习，获得基于前面两种模型基础上的互联网金融指数的二次训练模型，使得预测精度进一步提高。仍然使用互联网金融数据的前80%作为训练数据集，即是在预训练模型的基础上进一步进行数据的训练，20%作为预测数据集。

图4 和图5 为基于标准普尔500 迁移学习后的模型结果图。

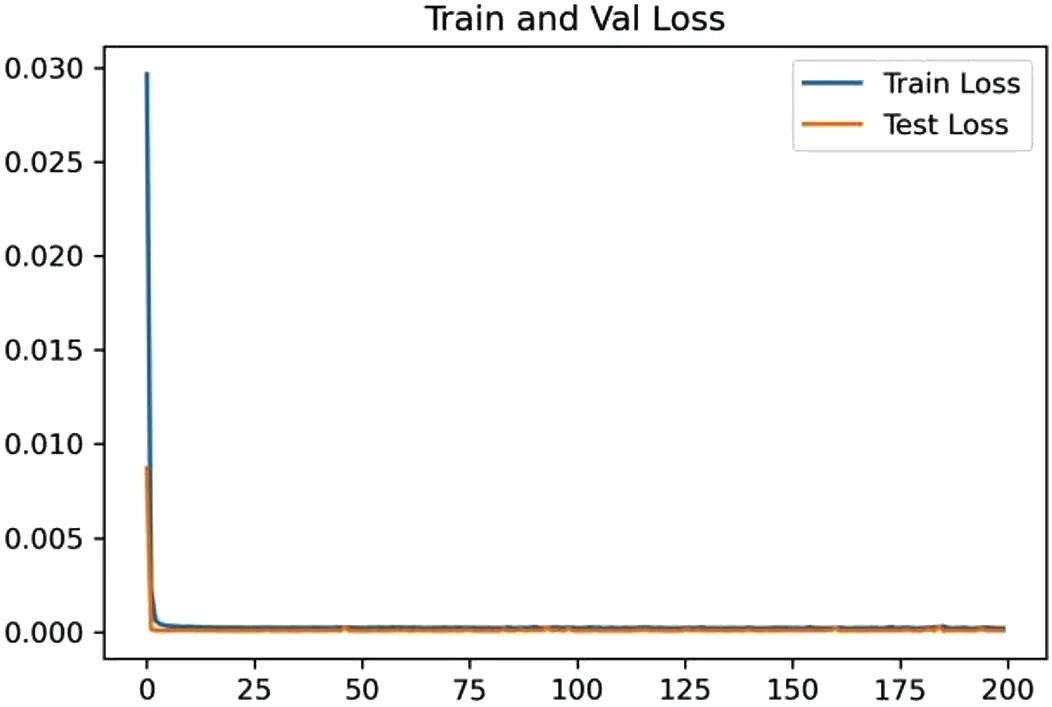
图4：基于标准普尔500 的迁移学习模型损失函数

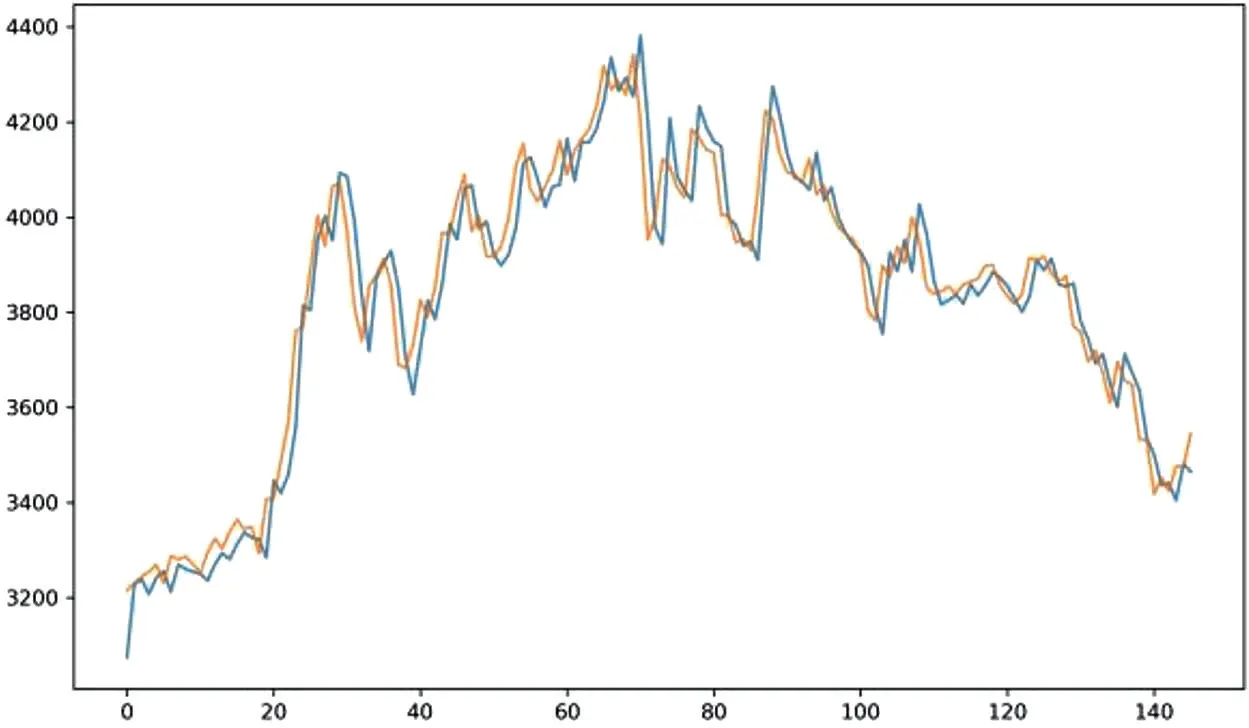
图5：基于标准普尔500 迁移学习模型的真实值与预测值对比

迁移后的模型的预测值与真实值的平均绝对误差（MAPE）值为1.024%，比原来下降了1.052%。

图6 为基于恒生迁移学习后的模型结果图。

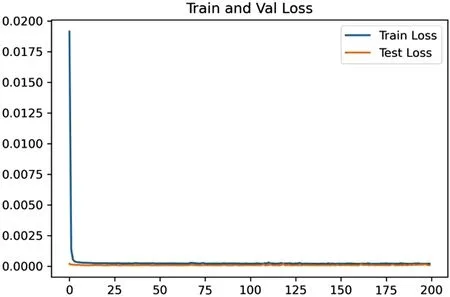
图6：基于恒生指数迁移学习模型的损失函数

迁移后的模型的预测值与真实值的平均绝对误差（MAPE）值为1.330%，比原来下降了0.746%。由此可以得出，在同样数据量的条件下基于标准普尔的数据模型的预测值与真实值的误差更小，预测结果更为准确。

5 结论

本文利用卷积神经网络与迁移学习相结合的模型进行预测互联网金融指数，首先在卷积神经网络上进行数据的训练预测形成预测模型，然后再选取互联网金融数据的部分数据再前面的预测模型上进行第二次的数据训练形成迁移后的新模型，用该模型进行预测，通过代码运行结果和图形显示可知在一定的程度上提高了准确度。此外，用卷积神经网络进行股指数值的预测在一定的程度上具有较好的预测效果，表明了用一维卷积神经网络进行数据预测是可行的。当预训练模型的数据量相当时，标准普尔500 的预测准确度较高，标准普尔的走向趋势与互联网金融指数数据相似度更高。