非相称分数阶多智能体系统脉冲一致性设计

林万丽

（广东工业大学自动化学院 广东省广州市 510006）

1 引言

近年来，研究者们发现在复杂环境中，有许多物理系统及机器因其特殊的材质和性质而表现出分数阶动力学行为，例如正弦振荡器、随机扩散、人群体编队、地震分析、粘弹性阻尼器等。因此，分数阶微积分系统逐渐地引起了研究人员的极大兴趣。

在现有的研究成果中，分数阶微分系统在多智能体系统的研究相对来说还是比较少。分数阶多智能体系统（FOMASs）作为一种特殊复杂网络系统，具有相对先进的科学课题。多智能体系统的协调控制以其高效、鲁棒性强等特点，在无人机群、分布式传感器网络、智能交通运输等领域引起了广泛的关注。多智能体系统的一致性是协调控制中的一个最基本问题，已经得到了广泛的研究，其目的是设计一个仅使用有限的局部信息的分布式算法，使所有智能体的状态在任意初始条件下都能达成一致。因此，研究FOMASs的一致性问题具有十分重要的理论和现实意义。

文献首先考虑了分数阶线性系统的一致性问题，其中一致性是由所设计的控制器实现的。此外，随着分数阶微分逐渐被人们重视起来，在文献中，Gong 等学者基于神经网络的鲁棒自适应控制上，设计了一些分布式跟踪协议。文献中提出了一个观察器来处理奇异分数阶多智能体系统领导-跟随一致问题。文献学者们在固定有向图上，研究了具有动态前导的异构非线性分数阶多智能体系统的一致跟踪问题。为了实现FOMASs 的一致性，研究者提出了许多控制方法，如自适应控制、滑模控制、鲁棒控制、脉冲控制等。

脉冲控制作为一种离散时间控制方法，可以不连续地占用通信信道，且有效地节省网络带宽资源的消耗。由于其突出的优点，分数阶微积分系统的脉冲控制方法引起了研究者的广泛关注。

在文献中，学者们利用脉冲控制方法分析了FOMASs 中具有固定和切换拓扑的聚类一致性。文献进一步考虑在时滞的情况下，分析了具有混合时变时滞分数阶非线性多智能体系统的领导跟随指数一致性。此外，在脉冲控制的帮助下，文献利用事件触发脉冲控制方法研究分数阶微分混沌系统的同步问题，该方法综合了脉冲控制和事件触发控制的优点。脉冲序列由一定的触发函数和触发条件定义，它们与主从系统的状态有关。控制器只在脉冲瞬间更新。通过降低控制器的更新频率，可以进一步降低控制器对通信带宽和计算资源的消耗。

上述研究成果都是基于相称的分数阶系统的分析，而非相称的分数阶系统被研究的相对比较少。在现有的文献中，如文献中提出了一种新的模糊自适应控制器来实现两个不相称分数阶混沌系统的适当广义投影同步。假设主系统和从系统具有结构不一致、外部动力扰动、不确定模型和明显分数阶，然后用自适应模糊系统估计一些未知的非线性函数。最后，采用李亚普诺夫方法推导了闭环系统的参数自适应规律，证明了闭环系统的稳定性。

基于上述的分析，本文提出了一种非相称分数阶多智能体系统牵引脉冲一致性的设计。基于领域变量的基础，Lyapunov 方法和牵引脉冲控制理论有以下三个优点：

（1）该方法控制成本低，收敛速度快；

（2）脉冲增益不仅取决于脉冲函数还取决于系统阶数；

（3）该方法操作简单，易于实现，更适合工程应用。

符号说明：N表示正整数的集合，R 为实数集和R是正实数集。N 定义为跟随者的数量，当N∈N时，N={1,2,...,N}是一个有限集。R和R表示n 维实数空间和n×n 个实数矩阵的集合。λ(A)表示实对称矩阵A 的最大特征值，定义对角矩阵为M=diag{m,m,m,...,m}。

2 问题描述

2.1 图论

2.2 Caputo分数阶导数和Mittag-Leffler函数

函数y(t)的Caputo 分数阶导数定义如下：

2.3 相关定义和性质

2.4 模型描述

考虑由N 个跟随者和一个领导者的FOMASs 的动力学模型为：

其中系统阶数为，是领导者的状态向量。

注释1：系统（1）和（2）中阶数α ≠β，表示该系统是非相称系统；在现有的成果中比如，系统阶数都是α=β，这样的系统表示相称系统，随着环境的复杂化，研究非相称系统会更加具有现实意义。

控制器设计如下：

3 主要结果

在本节中考虑了非相称分数阶多智能体系统的脉冲一致性，利用Lyapunov 方法和牵引脉冲控制理论推导出了一致性的充分条件。

定理1：基于假设1 和假设2 成立的情况下，如果

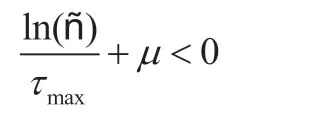
4 数值仿真

在这部分，为了验证提出的结果，直观地突出定理1，给出了一个数值例子。

假设FOMASs 由1 个领导者和4 个跟随者组成，则N=4。其拓扑图如图1 所示：领导者被标记为0，跟随者标记为1，2，3，4。

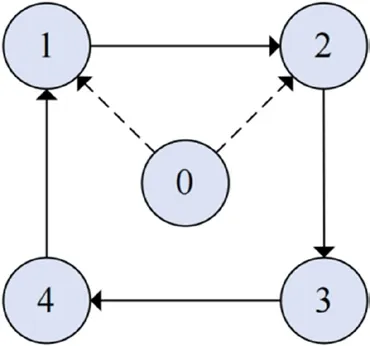
图1：系统拓扑图

图2 和图3 分别表达的是系统中智能体误差状态和牵引智能体的分布情况。通过图2 可知系统在牵引脉冲控制下能快速实现一致性。从图3 可以知道在每个脉冲时刻系统只牵引两个智能体，且这两个智能体在每个脉冲时刻都是变化的，其中变化的依据是由跟随者和领导者的误差大小来判断的，与领导者的误差越大的跟随者优先被牵引。

图2：系统中误差状态

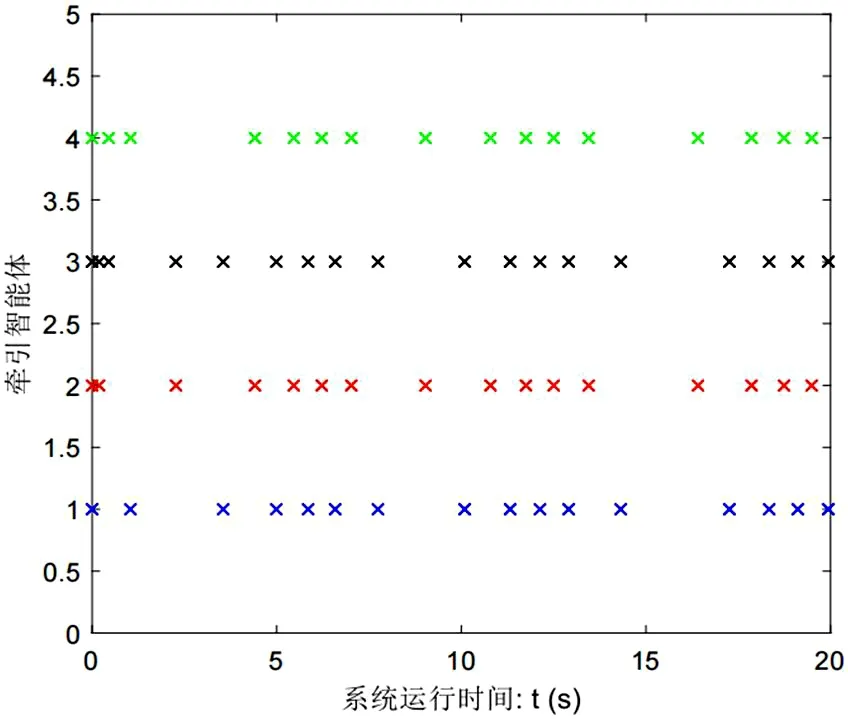
图3：牵引智能体

5 总结

为了解决非相称分数阶多智能体领导者跟随一致性问题。本文设计了一个领域变量函数，将分数阶系统转化为整数阶系统问题，实现多智能体系统一致性问题。通过利用Lyapunov 方法和牵引脉冲控制理论推导出了一致性的充分条件，同时获得更快的收敛速率。 研究结果表明，控制增益不仅取决于脉冲增益，而且还与系统的阶数有关。 最后，通过一个数值仿真，验证结果的有效性。