基于一种改进的CORDIC 算法的FFT 芯片设计

孔令甲

（中国电子科技集团公司第十三研究所 河北省石家庄市 050000）

快速傅里叶变换算法实现了信号从时域到频域的变换，运算速度快，在数字信号处理系统中应用广泛。FFT 算法利用DFT 运算旋转因子的对称性、周期性、可压缩、扩展性的特征来减少计算量，完成快速计算频谱的目的。FFT算法的硬件实现其硬件消耗主要集中在数据缓存和复数乘法碟形运算中，复数乘法运算算法是在单个或多个周期完成一次复数运算，运算量较大，复数乘法选择的运算的复杂性也会限制硬件的工作速度。

目前，为提高FFT 的精度和降低硬件消耗，一些研究者提出混合基等高基算法、可配置点数位宽、精度可调结构等方案来改进传统的radix-2FFT 算法和结构。但这些算法结构复杂，只是在精度或者速度等单个指标性能较优，没有在硬件面积、速度、精度等方面达到一个比较均衡的结果。FFT 处理器每一级运算需要进行一次碟形运算，传统的FFT 实现方式是提前把碟形运算的旋转因子存储在内部存储空间ROM 中，之后通过读取ROM 模块，完成复数乘法运算，这需要消耗一定的硬件面积。

CORDIC 算法通过简单的多次加法与移位运算，可以完成复数乘法、模计算、三角函数计算等，硬件结构实现简单，在工程中应用广泛。但是在需要完成较高运算精度的情况下，传统的CORDIC 迭代次数较高，会影响FFT 的实时处理速度。当FFT 运算点数越多，运算级数越多的情况下，CORDIC 迭代运算带来的时间消耗成倍增加。

本文提出了一种改进的CORDIC 算法实现复数乘法运算，通过改进单次迭代角度和旋转方程式，改进当前选择角度判断方程，在实现同样计算精度的情况下可以将迭代次数减半，减少蝶形运算时间，提高FFT 运算速度。蝶形运算的旋转因子的旋转系数通过控制模块内部实时产生，从而减少ROM 开销，减小FFT 硬件面积。通过合理的设置CORDIC 算法迭代次数和每次运算的数据截断位数，可以实现较高的FFT 运算精度。

1 原理分析及设计

1.1 CORDIC算法原理

坐标旋转数字计算CORDIC 算法是由Jack E. Volder于1959 年提出来的，当时主要用于实时飞行计算，此后CORDIC 算法在各个领域获得广泛的应用。

CORDIC 算法分为矢量方式（Vector Mode）和旋转方式（Rotation Mode）两种旋转方式。矢量方式是给定一个矢量的X、Y 坐标，计算该矢量的大小（平方和的平方根）和角度；旋转方式是给定初始矢量的X、Y 坐标以及要旋转的角度，计算旋转后矢量的大小和角度。

矢量方式是由旋转方式派生出来的，在旋转方式中，将初始矢量旋转到角度为0，则转过的角度即为初始矢量的角度的负数，而新的X 坐标与初始矢量的大小成正比。该比例系数为常数K。对于矢量模式、旋转模式和圆旋转、线旋转的四种不同组合，可以分别完成不同的运算。具体来说，在笛卡尔坐标平面上将点P(x,y)逆时针旋转θ 角度得到P(x,y)，CORDIC 算法的基本思想是将旋转角度θ 分解成一系列小角度θ，逐渐逼近θ。规定单次旋转的小角度θ正切值为tanθ=2，则小角度旋转角度正切值和坐标值乘法可以通过移位完成。

点P(x,y)，逆时针旋转θ 角度到P(x,y)。

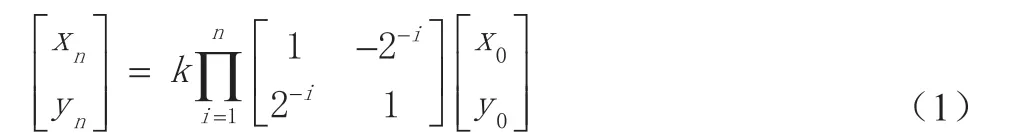
经过多次旋转角度迭代，伪旋转的幅度偏差可以近似为一个固定值：

表1：判决因子

经过伪旋转，P(x,y)旋转到正确的角度，但模值增加1/cosθ 倍，伸缩因子可以通过查表得到。

从而坐标旋转转换成简单的加减法和移位操作。

1.2 改进的CORDIC算法

根据以上的推导分析，CORDIC 算法的旋转次数选多，越逼近真实的目标值，得到的计算精度越高。但是，越多的迭代次数也意味着更大的延时和硬件消耗。本文提出改进的CORDIC 算法，增加每次的迭代角度选择判定，减小迭代次数，从而减少计算时间。由式（6）可得：

根据新的伪旋转方程式和角度累加方程式，新的 历次迭代角度如表2 所示。

表2：改进的CORDIC 算法历次旋转角度

则改进的方程式只需传统的CORDIC 算法的一半迭代次数，即可以达到相同的计算精度，从而减少了迭代运算带来的计算延时，提高FFT 实时处理能力。

1.3 改进的CORDIC算法在FFT硬件实现中的应用

1.3.1 复数乘法

本文采用基4-FFT 算法完成芯片设计。设输入序列长度为N=4M（M 为正整数）。

当序列点数满足N=4时，可以将x(n)分解抽取，n 分为4m、4m+1、4m+2、4m+3，将该序列按时间顺序的奇偶分解为4 个子序列有：

基4 FFT 运算在每次碟形运算之前先进行复数乘法运算（），包含四次乘法两次加法，运算量较大。

基4 FFT 算法单个碟形运算流图如图1 所示。

图1：基4 碟形运算

每一次碟形运算完成之后需要进行3 次复数乘法，而单次复数乘法需要完成如下运算：

式（9）、（10）分别代表复数运算结果的实部和虚部。因此，复数运算可以看作是数据旋转-2nkπ/N 角度。利用CORDIC 算法，多次累计迭代标定z角度，累加θ(n)无限逼近目标旋转角度值z(0)（-2nkπ/N），如果前一次累积旋转级数角度z大于目标旋转角度z(0)，则当前累积旋转角度z减去θ(n)，为此次顺时针旋转角度θ(n)。如果前一次累积旋转级数角度z小于目标旋转角度z(0)，则当前累积旋转角度加上θ(n)，为此次逆时针旋转角度θ(n)。迭代次数越多，幅度偏差K 值近似为常数0.60725。

CORDIC 算法实现复数乘法结构框图如图2 所示。

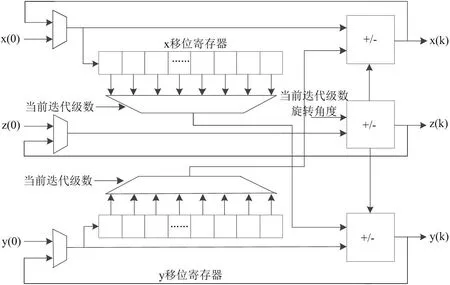
图2：CORDIC 算法实现复数乘法结构框图

数据传输给复数乘法模块前首先进行预处理，根据z(0)初始值将初始数据做取反和符号位预处理，操作预旋转π/2或π，后面的CORDIC 迭代旋转角度在[π/2, π]区间，之后通过CORDIC 算法迭代使z(k)逼近0，完成复数乘法运算。旋转因子不需要预先计算存放在ROM 表中，FFT 处理器根据当前运算的级数和数据位置由内部状态机实时产生旋转因子的系数nk，之后给串行流水线结构完成复数乘法和其他运算，这样节约了选择因子ROM 存储表带来的硬件消耗。

1.3.2 基于CORDIC 算法的FFT 硬件设计

FFT 设计采用串行流水线单路延时置换结构。1024 点FFT 由5 级流水线完成，，第一级碟形单元包含深度为256的3 块RAM 进行数据缓存，后面级数依此类推，各级数据缓存寄存器数量消耗为64..4/1，后四级数据缓存数量少，直接用寄存器代替RAM。

每一级碟形单元调用CORDIC_BF 单元进行一次复数运算。控制模块内部计数器根据当前每一级运算数据序列位置实时产生旋转因子系数给CORDIC_BF 单元。FFT 运算完成，运算结果输出实部和虚部给CORDIC 幅值运算单元完成模值运算。控制模块内部计数器根据当前每一级运算数据序列位置实时产生旋转因子系数给CORDIC_BF 单元。

FFT 硬件实现结构框图如图3 所示。

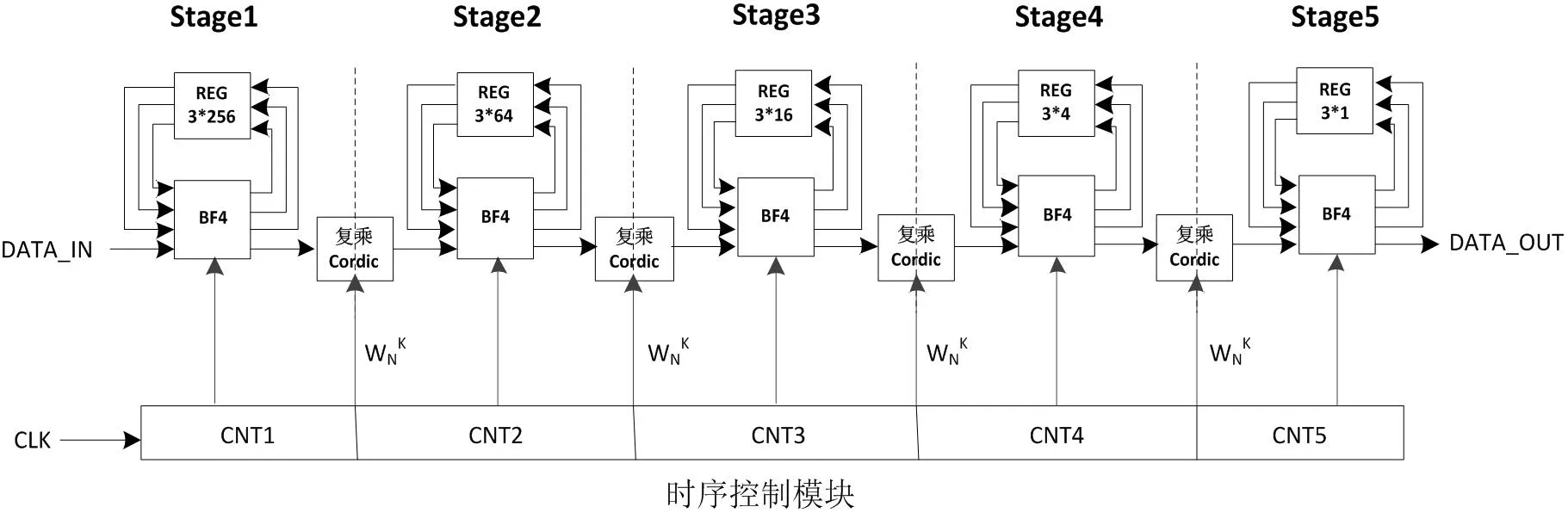
图3：FFT 硬件实现结构框图

数据采用定点运算，输入数据为12bit，为提高计算精度减少截断误差，选择因子系数为12bit ，选择CORDIC 运算迭代次数为12 次。在数据输入时首先进行零值检验判定，减少计算误差。采用上述结构，用VERILOG 语言完成1024点FFT 运算模块设计，通过VCS 进行仿真验证，利用MATLAB 内部FFT 算法作为标准参考输出验证设计。

2 结果分析

采用0.18um 工艺对设计进行时序综合和后端版图设计并流片。搭建芯片测试平台，验证FFT功能，图4为测试结果。

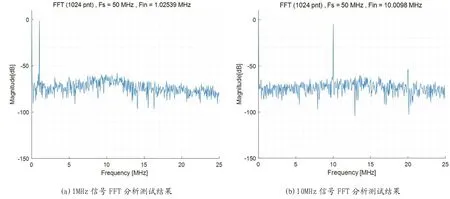
图4：芯片测试结果

表3 为本设计和部分参考文献的设计结果对比。

表3：结果对比

本设计的测试结果SNQR 有一定优势，信号量化噪声是数据位宽、截断误差等多方面的影响，结果可以说明基于改进的CORDIC 算法完成的FFT 处理器具有较高的运算精度。同时，基于CORDIC 算法采用流水线型SDF 结构完成的FFT 模块与通用复数乘法方案面积优势较大。综合面积、精度、计算时间几个指标，本设计方案具有一定的优势。

3 结论

基于改进的CORDIC 算法完成的FFT 复数运算模块通过多次迭代完成碟形运算，可以减少通用复数乘法运算时间，提高FFT 实时处理能力。同时，CORDIC 算法模块可以复用在FFT 的复数求模运算中，在相同的运算精度的情况下减少CORDIC 算法迭代次数。FFT 运算旋转因子的旋转系数通过控制模块处理器内部实时产生，不需要提前存储旋转因子，减少了ROM 开销。同时通过合理的硬件结构和数据位数、截断位数分配，此方案可以实现较高的计算精度和计算速度，在工程应用中具有一定的优势。