基于主成分分析的光通信神经网络均衡算法

江逸宁 滕旭阳 孙雨潼 毕美华

（杭州电子科技大学通信工程学院 浙江省杭州市 310018）

1 引言

目前，下一代接入网技术（Next Generation Passive Optical Access Network, NG-PON）研究的重点主要集中在系统容量100Gb/s 下的单波长25Gb/s 速率及其相关技术。同时，PON 系统也需要在实现高容量的基础上保持低成本。在传输技术方面，强度调制直接检测（Intensity Modulation Direct Detection，IM-DD）和相干传输技术是目前主流的传输技术。其中，相干传输由于接收机结构复杂度高等原因，不利于成本控制。因此，基于IM-DD 的光传输技术基于其低复杂度低成本的特性，主要运用于中、短距离光通信传输系统。而在短距离光通信系统中，四电平脉冲幅度调制（4 Pulse Amplitude Modulation,PAM-4）具有较低的功耗以及更简单的结构，对带宽要求低，从而降低了每比特的成本，得到了广泛应用。由于系统中存在的非线性失真与码间串扰（ISI，InterSymbol Interference）将严重影响系统性能。目前研究的低成本高带宽NG-PON 系统通过在发送端或接收端采用了均衡技术来补偿非线性损伤与ISI 影响的传输性能。国外如Hao Ying等人的研究中，利用FFE 均衡器(Feed Forward Equalizer)结合BP 神经网络(Back Propagation Neural Network)，对非线性失真进行抑制，提升了均衡器的整体性能，但对ISI 的补偿性能精度不够。而Jing Zhang 等人提出了运用卷积神经网络进行光通信均衡来降低系统的误码率，缺乏对前后码元及其相关性的分析。同时，韩国KAIST 将简化版的Volterra 非线性均衡器应用于光传输系统，其中NG-VNLE 通过简并二阶Volterra 项而大幅减少了系统复杂度，而该操作也忽略了ISI 补偿过程中的相关性致使信息损失。因此，本文基于滑动窗口，提出了一种基于滑主成分分析法的深度神经网络算法，在保证较低复杂度的同时，补偿了光通信系统中的非线性损伤。在距离为20km时，以发射功率为-14dBm 的80Gb/s PAM-4 信号系统为例与Volterra 非线性均衡器相比，本文提出的方法可以有效提高均衡性能，将误码率降低至1.4×10。

2 神经网络非线性均衡器

2.1 基于滑动窗口法的深度神经网络

深度神经网络（Deep Neural Networks, DNN）是一种机器学习算法，具有多层隐藏层神经元，多个输入层神经元以及多个输出层神经元的线性或非线性方程，常利用其高维尺度适于对复杂数据结构分类的优势对多维特征进行分类。而基于滑动窗口，可以找到输入序列中存在数据波动的临界点，以该点的维数作为输入窗口的滑动长度。如图1 所示。

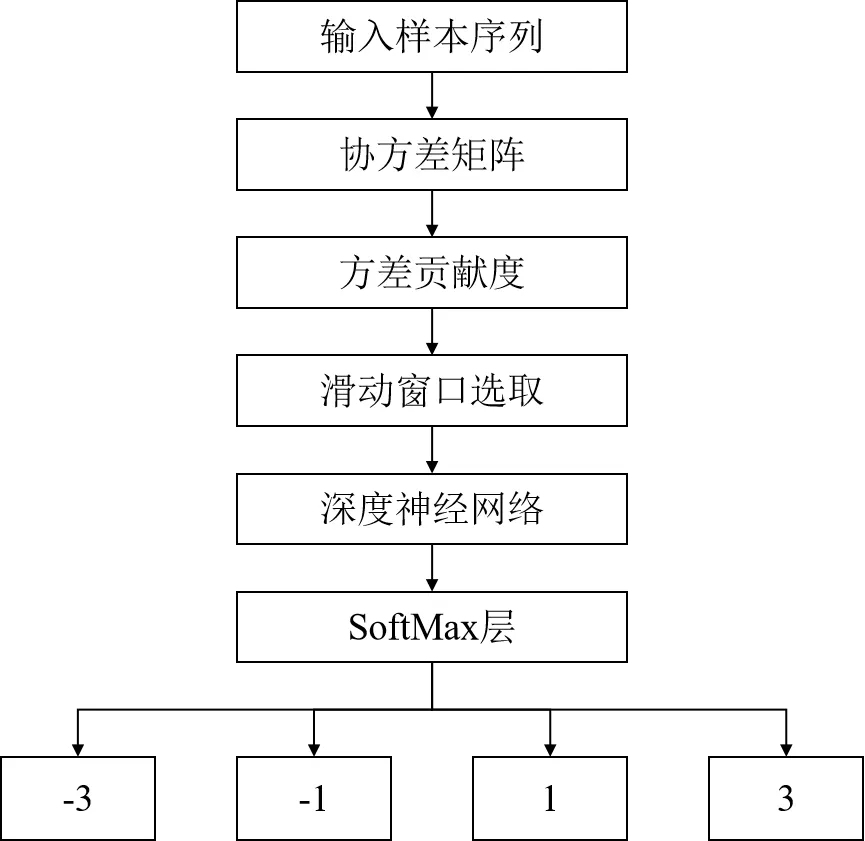
图1： 输入样本分类过程

假设每个样本序列中共有n 个样本，即X=(X,X,...,X)，每个样本对应的标签序列为：

Label=(Label, Label, ..., Label)

由于前后码元存在相关性，所以样本序列唯一对应标签序列中一个标签。定义数据波动的临界点长度为l，即滑动窗口的长度为l。假设需要通过神经网络分类器对第i 个样本进行分类。可以得到滑动后的窗口范围为[i-l:n-l]。如图2所示。

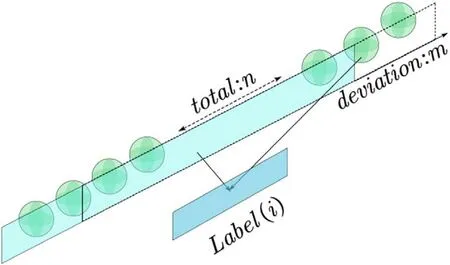
图2： 滑动窗口示意图

而相应的输入样本即为：

选择数据集中35%的数据用于评估检验。当检验误差在迭代过程中逐步减少时，学习速率也将随之降低。因此实际处理时，使用200000 个样本特征向量训练神经网络，其中35%用于验证，从而可用160000 个测试样本评价分类精度，初始学习率设为0.01。图3 的神经网络分类器具有2 层隐藏层的全连接前馈结构，使用ReLu 函数作为非线性函数。

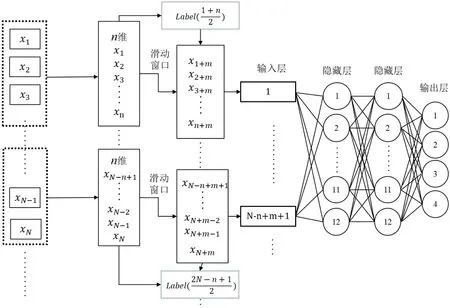
图3： 滑动窗口输入神经网络

为了尽量降低模型的复杂度，输入到输出各层的隐含节点数分别设为N-n+m+1、12、12 和4。输出层选用归一化指数函数 （Softmax）生成PAM-4 码型四种波形。

处理时需要先将输入到神经网络中的各个样本特征向量元素进行归一化后再进行序列划分与窗口滑动。不同于其他类型的机器学习方法，深度神经网络在特征空间维数较高的情况下能通过滑动窗口调节前后输入样本的比例，同时很好地从大量特征中提取有用信息，并提供良好的识别性能。

3 主成分分析

在输入网络前，前后码元之间存在相关性，即各输入码元具有内关性，通过计算输入特征的方差贡献率，可以得到码元序列所包含特征信息的情况。计算原始输入特征码元序列的协方差矩阵：假设在原始输入数据集中有N 个码元序列，每个序列中共有p 个样本，即X=(X,X,...,X)，其中X=(X, X, ..., X)。因此可将输入码元数据集的协方差矩阵A 表示为：

其中λ为协方差矩阵的特征值。通过对样本序列的方差贡献分析，可有效且直观观察输入样本序列的信息分布情况。当部分特征的累计方差贡献率达到95%时，对应的m 个主成分能够包含影响判决的大部分特征信息，并可以此为基准进行降维。而本文在实验过程中，将699维信息降维至399维。在整体特征信息分布较为平均时，同时结合滑动窗口法，抑制低信息量的方向样本在判决过程中的重要性，着重对反向的时间序列样本进行特征提取。

4 实验设计

4.1 数据集与实验配置

本数据集由发射功率为-1dBm 到-22dBm 的80Gb/s PAM-4 信号系统得到。其中不同发射功率下对应的数据集均有200000 个训练样本以及50000 个测试样本。

4.2 滑动窗口比例设置

在确定前后输入比例时，本实验将采用的样本数据集，按照14:1:14 的比例（即14 个先前样本、1 个当前样本、14个后续样本），分割成具有29 个样本数量的序列。在深度神经网络中，输入尺寸为199972×29，通过长度为4 的滑动窗口对序列对应标签值进行调整，即前后码元比例为5:9，模型可以抑制低信息量的方向样本在判决过程中的重要性，着重对反向的时间序列样本进行特征提取。如图4 所示。

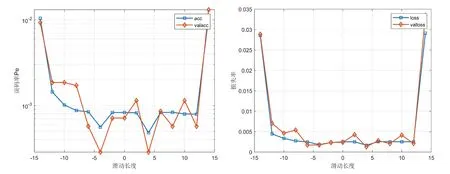
图4： 滑动长度对应的误码率与损失率

网络具有两层隐藏层，输入到输出各层的隐含节点数分别设为29、12、12 和4。优化器为rmsprop，其中初始学习率设为0.01，损失函数采用交叉熵损失。

为了更好地评估滑动窗口输入法的分类性能，设置步进为2，对基于不同滑动窗口长度所对应神经网络分类器性能进行对比。由图4 可知，当滑动长度过大，即彻底忽略先前样本或后续样本的信息时，训练损失迅速上升，误码率达到了1.06×10。当输入序列向后移动4 位时，即前后比例为5:9时，误码率最低，达到了2.86×10。

对传统的FFE 滤波器，DFE 滤波器等方法和本文的方法进行性能仿真比较，横轴表示训练的迭代次数，纵轴表示训练过程中得到的误码率，结果如图5 所示。其中将长度为4 的滑动窗口处理后前后样本比例为10:1:18 时的训练曲线，与未经处理的前后样本比例为14:1:14的训练曲线进行对比。

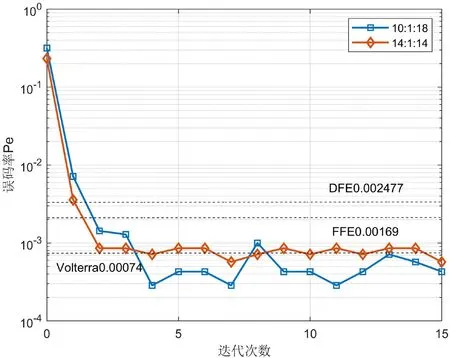
图5： 滑动窗口输入DNN 性能对比

由图5 可知，通过滑动窗口对深度神经网络进行处理，可以得到更低的误码率，且性能均优于传统的Volterra、FFE、DFE 等分类方法，且在前后输入码元比例为5:9 时效果达到最佳。

4.3 实验结果分析

训练长度和滤波器抽头数（神经网络输入层码元）是影响算法性能最大的两个因素。图6(a)为发射功率为-14Bm的80Gb/s PAM-4 信号数据的 BER 与滤波器抽头的关系曲线图。可以发现，本文方案在输入层码元数量为699 时效果最好，通过主成分分析法进行降维，将699 维降维至399 维，复杂度降低了42.918%。如图6(b)所示，可以得到本方案在不同训练长度下的 BER 性能。可以发现随着训练长度的增长，均衡精度提高并趋于稳定。

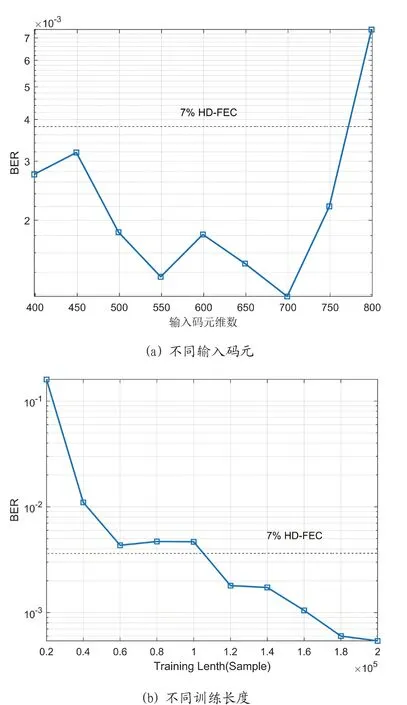
图6

为了提高均衡精度同时避免训练过程中产生的过拟合现象，对所有研究方案均采用了码元数量为100000 的相同训练长度，且使用了滑动窗口将前后输入码元比例确定在5:9。此外，通过主成分分析法将这将699 维降维至399 维，有效降低了实际应用中的复杂性和均衡开销。

对传统的FFE 滤波器，DFE 滤波器以及Volterra 滤波器等方法和本文的方法进行性能仿真比较，横轴表示不同接受光功率，纵轴表示训练过程中得到的误码率，结果如图7 所示。

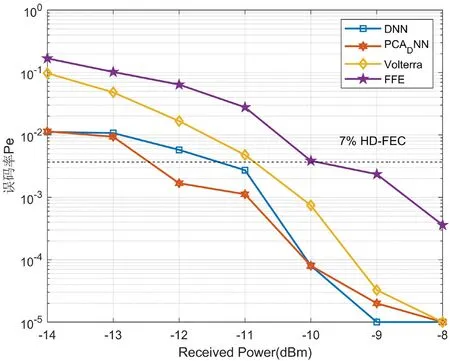
图7： 不同接受光功率下的误码率

其中将滑动窗口处理后前后样本比例为5:9 时，再从699 维降维至399 维的均衡训练曲线，与FFE、DFE 与Volterra 滤波器以及未进行降维的DNN 网络得到的误码率进行对比。

可以发现，通过滑动窗口与主成分分析法对深度神经网络进行处理，可以在降低42.918%复杂度的基础上得到得到更低的误码率，在接受光功率为-11dBm 时的误码率达到1.1×10，且性能均优于传统的Volterra、FFE、DFE 等传统方法。

5 结束语

本文利用滑动窗口长度对输入序列的前后样本比例进行调整，并基于多维输入样本特征的方差贡献率对输入码元序列进行主成分分析，对距离为20km 时，对发射功率为-1dBm到-22dBm 的80Gb/s PAM-4 信号系统进行实验，发现相比于DFE、FFE、 Volterra 等传统分类方法，本模型方法有着更高的分类准确度，可以在降低42.918%复杂度的基础上得到得到更低的误码率，在接受光功率为-11dBm 时的误码率达到1.1×10。