对一道不等式恒成立问题解法的探究

梁红涛

不等式恒成立问题是不等式板块中具有代表性的一类问题.这类问题的实质是使不等式的解集包含于某一个区间，但我们往往无法直接求出不等式的解集，此时通常需将问题进行转化，运用函数的图象、性质以及不等式、导数的性质来解题.下面结合一道例题谈一談如何解答不等式恒成立问题.

该题主要考查对数函数、二次函数以及不等式.该不等式中含有对数式，很显然，我们无法通过解不等式求得问题的答案，需将问题进行合理转化，从其他角度寻找解题的思路.通过分析，笔者找到以下的解题思路.

思路一：利用函数的单调性求解

利用函数的单调性求解不等式恒成立问题，要先根据不等式的特点构造合适的函数模型，然后根据导函数与函数的单调性、函数单调性的定义来判断函数的单调性，求得函数的最值.一般地，f（x）≥a恒成立可转化为f（x）≥a;f（x）≤b恒成立可转化为f（x）≤b.

当a>l时，x→0，logx→-∞，x→0，

∴f（x）→-∞，这与f（x）>0相矛盾，

我们还可以将不等式中的参数a分离，然后构造函数，再利用导函数与函数的单调性之间的关系来判断函数的单调性，进而求得最值，这样也能将问题转

化为函数最值问题，从而求得参数的取值范围.

当a>1时，不满足题意;

思路二：借助函数的图象求解

对于形如或者可以变形为f（x）>（<）g（x）的不等

式，我们可采用数形结合法，借助函数的图象来分析

问题.首先画出函数y=f（x）和y=g（x）的图象，然后借助图形分析两个函数图象之间的位置关系，讨论使不等式恒成立的临界情形，据此建立关系式，求得问题的答案.

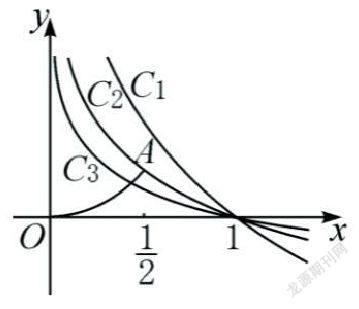
解：由logx-x>0得logx>x，

设y=logx，y=x，

当a>1时，不满足题意;

可见，函数的单调性和图象是解答不等式恒成立

问题的重要工具.因此在解题时，同学们要学会将不等式恒成立问题与函数关联起来，将问题转化为函数问题，利用函数的单调性、图象来解题.