设而不求,提升解答圆锥曲线问题的效率
2022-07-11桂燕
桂燕

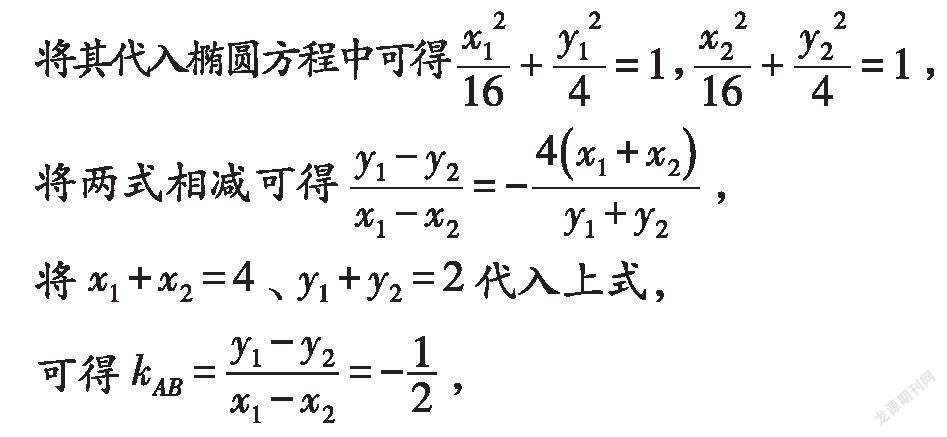



设而不求法是解答高中数学圆锥曲线问题的常用方法之一.运用该方法解题,需根据题意,找到问题中所求目标与已知条件之间的联系,并设出相关的参数,如直线的斜率、方程、点的坐标、曲线的方程等,然后将其代入题设中进行求解.下面谈一谈如何巧妙运用设而不求法求直线的方程以及求解定值问题.
一、求直线的方程
圆锥曲线问题中的求直线方程问题通常涉及直线与圆锥曲线的位置关系.采用设而不求法解答此类问题,需从直线与圆锥曲线的位置关系入手,根据其位置关系设出切点、交点的坐标、直线、曲线的方程等,然后将其代入题设中进行运算,得到直线的斜率、方程.
解:设弦所在的直线与椭圆交于A(x,y),B(x,y)两点,
将x+x=4、y+y=2代入上式,
故所求直线方程式为x+2y-4=0.
解答本题主要采用了设而不求法,先根据直线与椭圆相交,设出两个交点的坐标,然后将其代入椭圆方程中,并作差,便可根据直线的斜率公式和中点坐标公式得到弦所在直线的斜率、方程.
二、求解定值问题
圆锥曲线问题中的定值问题比较常见,但难度较大,一般要求根据题意求证直线恒过的定点、某条线段的长为定长、某两个线段的比值为定值、某个代数式的值为定值等.在采用设而不求法解题时,可根据题意设出相关点的坐标、直线的方程、曲线的方程等,然后根据弦长公式、韦达定理、两点间的距离公式、勾股定理、圆锥曲线的性质等求得定值,或者得到与变量无关的式子.
得(9-16k)x+160kx-400k-144=0,
設点A(x,y),B(x,y),AB的中点N(x,y),
令y=0可得x=ky+x,
可见,采用设而不求法求解圆锥曲线问题,能有效减少运算量,提升解题的效率.而采用设而不求法解题的关键是设出合适的参数,用以表示出直线的方程、曲线的方程、目标式.一般地,可根据题意设出与已
知条件、所求目标关联较多的变量,这样便于将未知量与已知量关联起来,根据已知条件、定义、性质、公式等求得目标式,再通过消参或代换,达到解题的目的.
