怎样选择合适的方法来求函数的解析式

周必辉

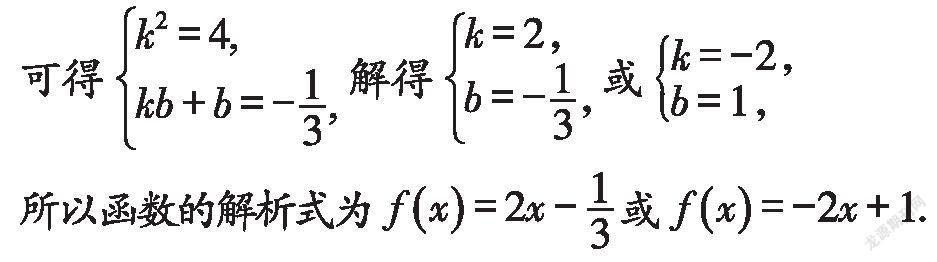
求函数的解析式问题主要考查函数的定义域、基本函数的图象、性质.此类问题的难度不大，在解题时只要能选择合适的方法，便能快速求得问题的答案.

一、待定系数法

待定系数法是指将多项式表示成另一种含有待定系数的新形式，进而得到一个新的恒等式，根据恒等式的性质得到系数应满足的方程或方程组，然后通过解方程或方程组，求出待定的系数或找出这些系数应满足的关系式.运用待定系数法求函数的解析式，需先根据函数的类型，引入待定系数，设出函数的解析式，再把题设中的条件代入，建立方程（组），求得待定系数的值，即可求得函数的解析式.

例1.已知f（x）是一次函数，且f（f（x））=4x-1，求f（x）的解析式.

分析：由于函数的类型已确定，所以只需根据一次函数的表达式，引入待定系数k、b，设出函数的解析式f（x）=kx+b（k≠0，b为常数），根据题意建立方程或方程组，求得待定系数k、b的值，即可求得函数的解析式.

解：设f（x）=kx+b（k≠0），

则f（f（x））=f（kx+b）=k（kx+b）+b

=kx+kb+b=4x-1，

利用待定系数法求函数的解析式，需熟练掌握各类基本函数的表达式，这样才能引入合适的待定系数，设出正确的函数解析式.

二、换元法

换元法是将代数式中的某一部分用一个或几个新的变量替换的方法.换元法主要适用于求解代数式较为复杂或复合函数的解析式問题.在解题时，可将代数式的某一部分或复合函数f（g（x））中的g（x）用一个新元替换，得到关于新元的式子，再将新元用x替换，就能得到函数f（x）的解析式.

运用换元法求函数的解析式，要注意换元前后自变量的取值范围，以确保得到正确的函数解析式.

三、方程组法

当已知关系式中的自变量之间互为倒数或互为相反数时，可通过构造新方程来解题.

上述三种方法均是求函数解析式的常用方法，每种方法的适用题型各不相同，同学们在解题时，要仔细审题，若已知函数的类型，可采用待定系数法;若由复合函数求函数的解析式，可采用换元法;若遇到含有与f（x）相关的关系式，可采用方程组法求解，同学们要学会根据解题需求选择合适的方法进行求解.