由一道多元变量最值题引发的思考

王金萍

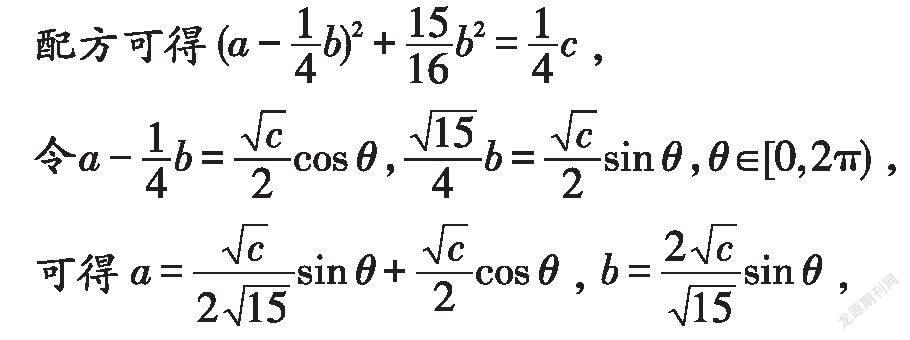
多元变量最值问题中通常会涉及两个或两个以上的变量，因而此类问题的难度一般较大，且对同学们的代数运算、逻辑推理、数学抽象等能力有较高的要求.对此，笔者对一道典型的多元变量最值问题及其解法进行了研究，下面谈一谈个人的一些看法.

一、问题呈现

二、解法分析

方法1.基本不等式法

解：由4a-2ab+4b-c=0可得4（a+b）=c+10ab

通过对方程进行变形，得到ab，便可利用基本不等式得到关于的不等关系式.再根据二次函数的性质，分两个情况：a=b>0和a=b<0讨论a+b+c的最值.

方法2.判别式法

对于有关二次方程、函数、不等式的最值问题，我们都可将问题转化为一元二次方程问题，利用方程的判别式来建立不等关系式.一般地，若变量的取值范围为R，则判别式△≥0;若方程无解，则判别式△<0，据此建立关于目标式的不等式.通过解不等式，即可确定目标式的最值.

解：设a+b=t，则b=t-a，

将其代入4a-2ab+4b-c=0，整理可得10a-10at+4t-c=0，

显然，关于非零实数a的二次方程有实数根，

结合题目中的已知条件，将目标式进行换元，便可构建出一元二次方程，利用方程的判别式法来建立不等式，根据不等式的性质来巧妙地将关系式a+b+c转化为二次函数式，再利用二次函数的图象与性质，就能求得最值.

方法3.三角换元法

三角换元法是解答二元变量最值问题的常用方法.在解题时，可根据同角的三角函数关系式：sinθ+cosθ=1進行换元，如令x=sinθ、y=cosθ，将其代入题设中，便将问题转化为三角函数最值问题，根据三角函数的单调性、有界性、图象求得最值.

解：由4a-2ab+4b-c=0可得4a-2ab+4b=c>0，

方法4.权方和不等式法

解：由4a-2ab+4b-c=0 可得4a-2ab+4b=c>0，

方法5.导数法

导数法是解答有关函数、不等式、方程的最值问题的重要工具.在解题时，需首先根据题意构造出函数模型，然后对其进行求导，通过分析导函数与0之间的关系，判断出函数的单调性，确定极值;或根据导函数的几何意义来确定临界情形：曲线与直线相切，顺利求得最值.

解：设f（a）=4a-2ab+4b-c，

把b=a代入4a-2ab+4b-c=0可得c=6a，

根据题意以a为自变量、b为因变量、c为常数，构造函数f（a），通过求导，根据导函数的几何意义求得切线的斜率，便可找到a+b取得最大值时的临界情形，确定a、b的取值，从而根据关于c的二次函数式及其性质求得最值.

可见，基本不等式法、判别式法、权方和不等式法、三角换元法、导数法均是解答多元变量最值问题的重要方法.在解答多元变量最值问题时，同学们要学会将问题与函数、方程、不等式、三角函数、解析几何、导数等知识关联起来，从不同的角度寻找不同的解题思路.