谈谈比较指数、对数函数式大小的技巧

张杰

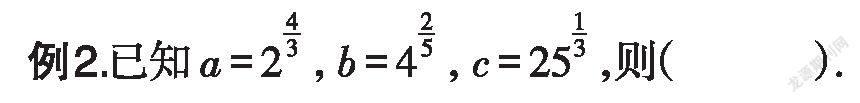
比较指数、对数函数式大小问题经常出现在函数试题中.解答这类问题，通常需灵活运用指数函数和对数函数的性质、图象、运算法则.对于一些无法直接利用指数、对数函数的性质、图象、运算法则比较出大小的问题，需采用一些小技巧，如取特殊值、化异为同、取中间量等来求解.

一、取特殊值

特殊值法是指选择一些满足题意的特殊值，通过代值、计算，从而比较出指数、对数函数式的大小.运用特殊值法解题，需先根据题设条件对未知量赋值，常见的有0、1、2、-1、-x等.通过取特殊值，可将运算过程化繁为简，这样有利于提高运算的速度和正确率.

例1.已知a>b>l，0<c<l，则（    ）.

A.a<b    B.ab<ba

C.alogc<blogc    D.logc<logc

所以D错误.

故本题选C.

二、化异为同

当遇到一些底数、指数、真数均不相同的指数、对数函数式问题时，可采用化异为同的技巧，根据换底公式，通过指数、对数函数互化，将指数、对数函数式化为底数、幂、真数相同的形式，再利用指数函数或对数函数的性质、图象来比较大小.

A.b<a<c    B.a<b<c    C.b<c<a    D.c<a<b

剖析：a、b、c均是指数函数式，可将其全部转化为底数相同的指数函数，再结合指数函数和幂函数在R上的单调性，比较出a、b、c的大小.

所以b<a<c，即A選项正确.

化异为同的技巧是比较对数函数和指数函数式大小的有效手段，主要适用于比较两个或两个以上指数函数或对数函数式的大小.

三、取中间量

有些指数、对数函数式之间的差异较大，直接利用函数的性质、运算法则等无法快速比较出它们的大小，此时，可以巧妙借助中间量来解题.根据题意确定一个中间量，通过比较待求值与中间量的大小关系，比较出指数、对数函数式的大小.

例3.已知a=log0.2，b=2，c=O.2，则（    ）.

A.a<b<c    B.a<c<b    C.c<a<b    D.b<c<a

解：因为a=log0.2<logl=0，

b=2>2=1，

0<0.2<0.2=1，

所以0<c<1，

因此a<c<b，故正确选项为B.

我们结合题意，以“1”为中间量，分别比较a、b、c与1的大小，进而确定a、b、c三者的大小关系.借助中间量比较指数、对数函数式的大小，需结合函数式选取合适的中间量，通常取0、-1、1等.因为loga=1、a=1（a≠0），这样便于转化函数式，比较出函数式的大小.

比较指数函数、对数函数式的大小问题的难度不大，常以选择题、填空题的形式出现.同学们在解题时，要结合题型、函数式的特点，选取合适的特殊值、中间量，化异为同，还要灵活运用指数、对数函数的图象、性质、运算法则等.