基于时延线阵列的毫米波NOMA 系统混合预编码设计和功率分配

孙钢灿，吴新李，郝万明，朱政宇,3

（1.郑州大学信息工程学院，河南 郑州 450001；2.郑州大学产业技术研究院，河南 郑州 450003；3.郑州大学电子材料与系统国际联合研究中心，河南 郑州 450001）

0 引言

随着5G 的普及，无线网络将会接入越来越多终端设备。毫米波（频率为30～300 GHz）具有丰富的频谱资源，可以为终端设备提供高速率数据传输[1-2]。另外，由于毫米波信号传输路径损耗较大，基站通常配备大规模天线以形成高增益的方向性波束。因此，毫米波大规模多输入多输出（MIMO,multiple input multiple output）已作为未来无线通信候选技术之一[3-4]。在传统大规模MIMO 中，为实现全数字预编码，每根天线连接一个射频链。但是，射频链功耗较大，大量射频链将导致较大的能量消耗。为降低系统功耗，稀疏射频链天线结构被提出，即少量射频链通过移相器连接到所有天线，这种结构降低了大量射频链带来的硬件成本和能耗[5-6]。非正交多址接入（NOMA,non-orthogonal multiple access）技术近几年获得较多研究，它通过串行干扰消除（SIC,successive interference cancellation）技术降低/消除用户间干扰，有效提高了系统频谱效率[7-8]。因此，结合以上两大技术构建基于NOMA的毫米波大规模MIMO 系统，可为未来无线网络提供高速率低功耗数据传输。

目前，相关文献已经对NOMA 技术在毫米波通信系统中的应用进行了较深入的研究。文献[9]研究了单射频链下毫米波NOMA 系统的功率分配和波束设计联合优化问题，提出了一种有效的优化方法。文 献[10]扩展到多个射频链，提出了一种基于K-means的用户分组算法，在此基础上设计了一种混合预编码和功率分配方案，实现系统谱效最大化。文献[11]以信漏噪比为性能指标，联合优化模拟数字混合预编码和功率分配以最大化系统谱效。文献[12]考虑了全连接和子连接2 种混合预编码结构，提出了一种低复杂度的功率分配算法以最大化系统能效。文献[13]研究了两用户下系统能效最大化问题，并提出一种基于Dinklebach 和拉格朗日对偶法的两层迭代优化算法，但其复杂度较高。文献[14]为最大化系统谱效提出了一种联合簇内和簇间的功率分配算法。文献[15]研究了基于开关反向器结构下系统的能效最大化问题，提出了一种两阶段功率分配策略。

然而在以上工作中，文献[9-13]研究的NOMA系统均基于高分辨率高能耗的移相器调制网络，这将导致较大的能量消耗。文献[14-15]研究的NOMA系统均基于开关反相器的混合预编码架构，虽然可以显著提高系统能效，但却造成频谱效率的严重损失。文献[16-17]提出通过简单的开关控制时延线阵列来实现连续相位调制，其硬件实现简单、功耗低。文献[18]将时延线阵列引入毫米波通信系统，研究了系统混合预编码设计问题，但其在基于NOMA的毫米波通信系统中的研究尚未开展。基于此，本文研究了基于时延线阵列的毫米波NOMA 系统的能效问题。

本文的主要研究工作如下。

1) 为实现连续相位调制及降低硬件设计复杂度，提出将开关控制的时延线阵列引入毫米波NOMA 系统，研究了系统能效最大化问题。为降低用户间的干扰，提出改进K-means 算法对用户进行分组，并为每组用户选择一个簇头；然后根据簇头集合组成的相关用户信道矩阵，设计了一种低复杂度的模拟预编码；之后采用迫零技术设计数字预编码以消除波束间用户干扰，并形成一个优化发送功率的能效最大化问题。

2) 针对上述所形成的非凸优化问题，提出了一种两层迭代算法。在外层应用Dinkelbach 算法将能效优化中目标函数的分式结构转化为相减结构；在内层将其转化为凸优化问题，提出一种交替优化（AO,alternating optimization）迭代算法。最后通过内外两层循环迭代获得最初问题的解。

3) 仿真结果表明，所提两层迭代算法在5 次迭代后即可达到收敛状态。与传统基于移相器的毫米波NOMA 系统相比，所提方案的系统能效和谱效分别提高了32.3%和10.7%。

1 系统模型

基于时延线阵列的下行毫米波NOMA 系统如图1 所示。将射频链和天线均进行分组，每个组中的射频链通过开关和时延线组成的时延线阵列网络连接到所有天线。假设基站配备NTX根发射天线和NRF个射频链，发射天线和射频链的分组数为m，K（K≥NRF）个单天线用户随机分布在基站覆盖范围内。为了充分利用系统的复用增益，假设波束数G等于射频链数量NRF[19]，将K个用户分为G个簇，定义每个簇的用户集合为Cg（g=1,… ,G），且Cg≥ 1。设第g个簇中第k个用户为(g,k)，每个簇内所有用户采用NOMA 技术进行数据传输。通过串行干扰消除技术消除弱信道增益用户对强信道增益用户的干扰[20]

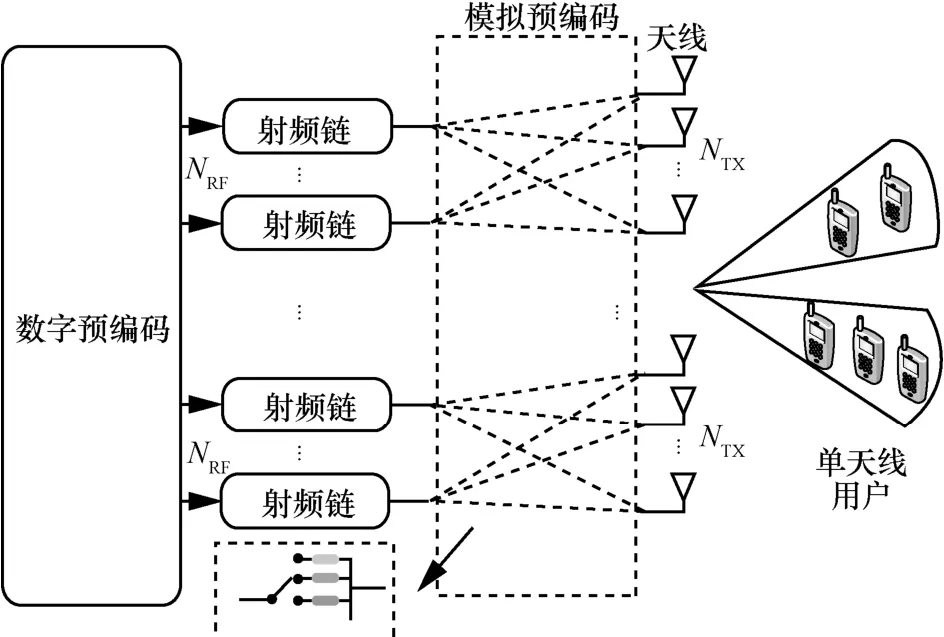
图1 基于时延线阵列的下行毫米波NOMA 系统

经过混合预编码之后，可以获得用户的等效信道增益，则用户(g,k)g k的接收信号为

其中，d和λ分别表示相邻天线的间距和信号的波长，满足；n1=0,…,N1，n2=0,… ,N2，N1和N2分别表示水平方向和垂直方向上的天线数，且NTX=N1N2。

2 用户分组和混合预编码

为充分利用NOMA 传输技术特性，降低不同波束之间的干扰，本文首先利用信道状态信息对用户进行分组，并找出每一簇中的簇头用户。然后，设计了一种两阶段混合预编码，在保证最大化天线阵列增益的同时，最小化用户间的干扰。

2.1 用户分组

为降低波束间干扰，可以尽可能提高同一簇用户信道的相关性，降低不同簇用户间的相关性。针对多用户的NOMA 技术，本文提出改进K-means用户分组算法，初始簇头通过最小化簇头之间的信道相关性进行选择。其中，用户k1和k2之间的信道相关性定义为[11]

定义选择的簇头集合为Ω={Ω1,Ω2,… ,ΩG}。根据式(4)计算剩余用户与每个簇头的相关性，并将相关性高的用户分在相应簇。分组完成后，为进一步减少波束间干扰，对每簇的簇头进行更新，选择每个簇中与其他簇具有最低信道相关性的用户作为新的簇头。定义单个用户与别簇用户的信道相关性之和为

因此，第g簇的簇头可以被更新为

当簇头被更新后，再根据式(4)进行用户分组。然后进行新一轮簇头更新，直到簇头不再变化，具体过程如算法1 所示。

算法1用户分组算法

2.2 模拟预编码

基于开关控制的时延线阵列结构如图2 所示，它是由复杂可编程逻辑器件（CPLD,complex programmable logic device）通过控制一个开关连接到4 条时延线来实现的[16]。在一个调制周期Tp期间，只选择2 条相邻的时延线。不同的时延线表示不同的相位时延[16]。每次选择的2 条时延线分别标记为α和β，开关接通α和β的持续时间为τ1和2τ。每根天线元件被相应的脉冲P(t) 调制，其幅度和相位如图3(a)和图3(b)所示。

图2 基于开关控制的时延线阵列结构

图3 脉冲p(t)的幅度和相位

将P(t)分解为傅里叶级数可得

由式(7)可得傅里叶系数pm为

其中，τ1和τ2分别表示时延线α和β上的脉冲持续时间，有τ=τ2+τ1≤Tp，在中心频率处有

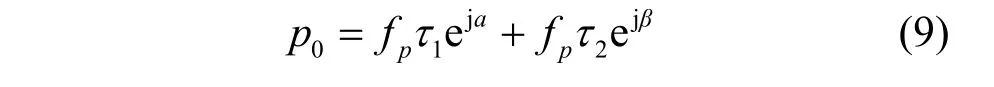
由于pTτ≤，式(9)可以改写为

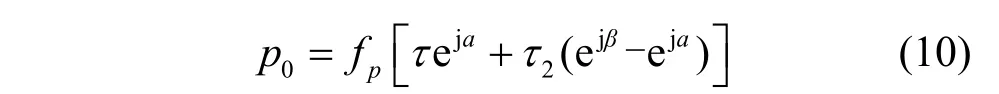
根据图2 可知，(α,β)有4 对可能组合，分别是，因此可以根据式(10)得到p0的可覆盖区域，即图4 的阴影部分。由图4 可知，在[0,2π]范围内给定天线的预期角度，则均可以通过时延线阵列控制实现，图4 阴影部分就是模拟预编码的可行域。

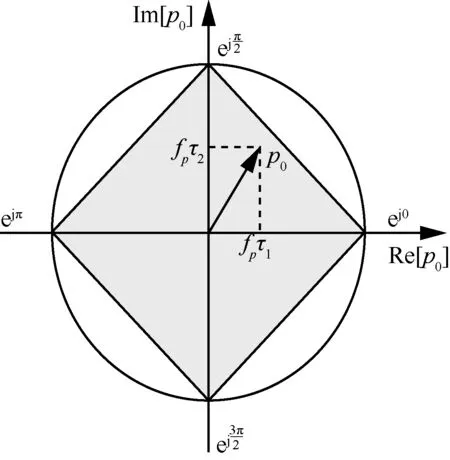
图4 p0 的可行域

在完成用户分组后，每簇中的用户与簇头具有高度相关性。所有簇头的信道矩阵可写为HΩ=[hΩ1,hΩ2,… ,hΩg]。本文提出的分组连接结构，模拟预编码A是块对角矩阵，即

其中，，且1,,jm=… 。从图4 可以发现，通过时延线阵列可以实现连续相位调制，同时在调节相位时其模拟预编码的幅度不受恒定的模值约束。受此启发，为了在增大用户阵列增益的同时降低用户间干扰。使用迫零技术构造低复杂度预编码矩阵作为中间变量，=，其中λ需要保证足够小，才可以满足预编码矩阵的所有元素都在矩形的可行域里。可得A中的每一列RF,ja为

2.3 数字预编码

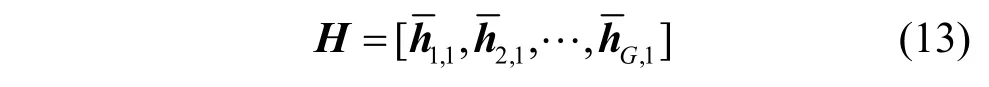
为消除波束间最强信道的干扰，使用经典的迫零技术可得数字预编码矩阵为

3 功率分配问题及其求解

在完成用户分组和混合预编码后，用户(g,k)的速率可表示为

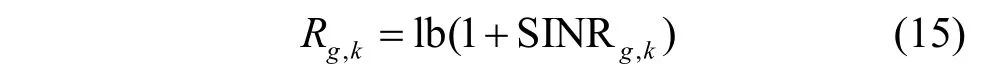
根据式(1)可得用户(g,k) 的信干噪比为

系统总速率可表示为

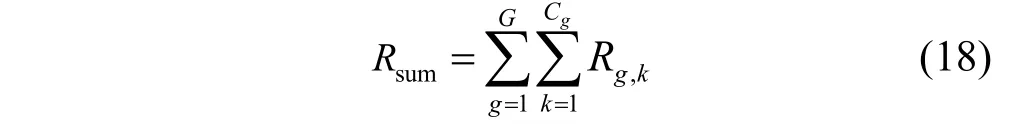
则系统能效定义为

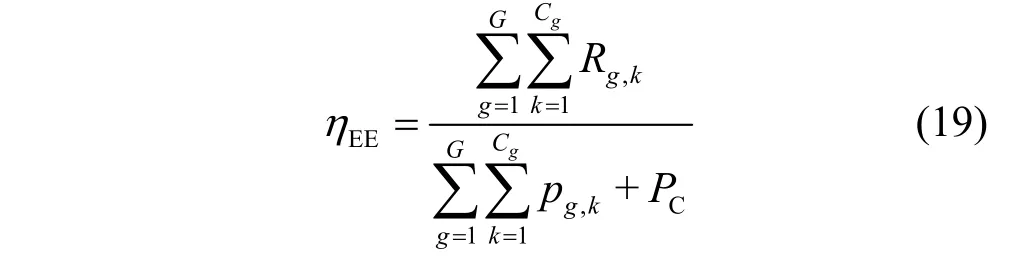
其中，PC是电路功耗，定义为

其中，PDL+SW=2PDL+PSW，PB、PRF、PDL和PSW分别表示基站、射频链、开关和时延线的电路功耗。因此，最大化系统能效问题可表示为

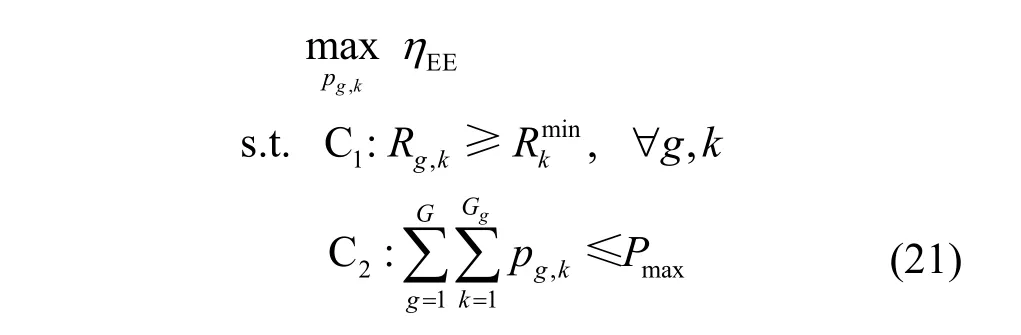
其中，C1表示用户服务质量约束，C2表示基站发射总功率约束。依据Dinkelbach 算法[22]，首先将式(21)中目标函数由分式规划问题转化为减法形式，即

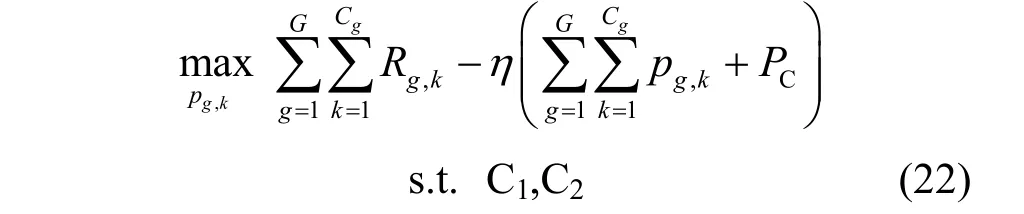
其中，η≥0。设式(22)的最优解为F(η)，式(21)的最优解为η∗，由Dinkelbach 算法可得[22]

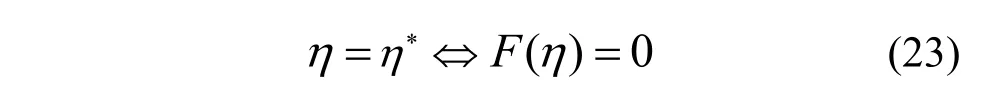
这意味只要找到F(η) 0=的根，则可以获得式(21)的最优解。当获得η时，需要重新求解式(22)。此时，式(22)的目标函数和C1约束仍然是非凸优化问题。首先，把式(15)和式(16)代入1C 中，将其转化为如下凸约束。

很明显，式(25)的前半部分是凸函数，同理，-lbζ g,k是非凸的，为了解决这个问题，引入引理1对其进行化简。

引理1定义函数y(t)=-xt+ln(t)+1，其中x是正实数，则有

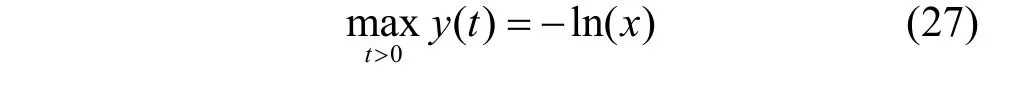
证明可以发现y(t) 是关于变量t的凹函数，则其最优值t∗可以表示为

将式(28)代入y(t)可得式(27)。

证毕。

根据引理1，式(25)可化简为

将式(29)代入式(22)可得等效的优化问题为

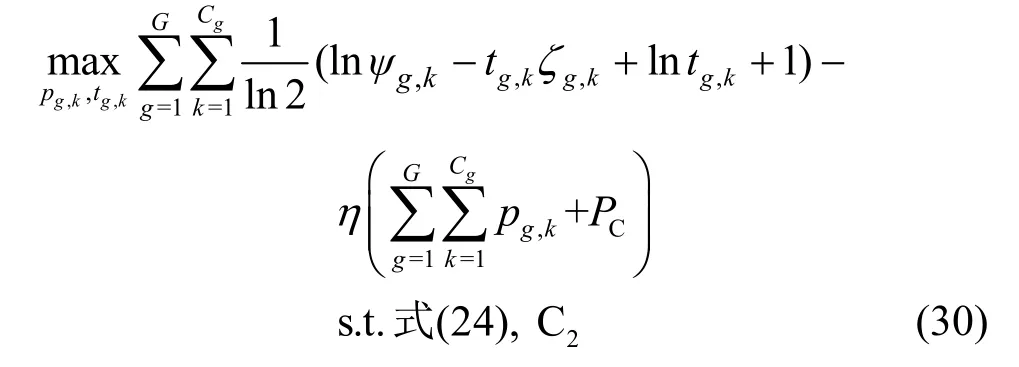
接下来，采用AO 算法，求解松弛变量tg,k和功率分配Pg,k。给定r-1 次迭代的功率分配，由式(28)和引理1 可得，在第r次最优的tg,k为

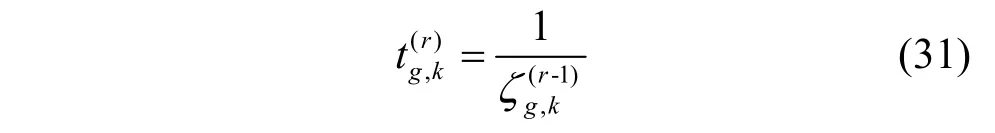
此时，式(32)是一个凸优化问题，可以通过凸优化工具CVX 对其直接求解[23]。最后采用本文所提出的基于Dinkelbach 算法和AO 的两层迭代算法得到原始问题式(21)的解。具体过程如算法2 所示。

算法2两层迭代算法

4 仿真分析

本节对所提方案性能进行仿真验证。具体仿真参数如表1 所示。

表1 仿真参数

表1 中，信道路径数目F=6包括一条可视路径和5 条非可视路径。m=1 代表全连接结构，m=2代表混合连接结构，m=4 代表子连接结构。另外，本文对比了传统基于2 bit 移相器的全连接和子连接混合预编码结构（简称为传统基于移相器全连接和子连接结构）以及基于全数字预编码结构下系统的谱效和能效。

所提算法的收敛性分析如图5 所示。其中，内层迭代收敛如图5(a)所示，可以发现5 次迭代后趋于收敛。外层迭代收敛如图5(b)所示，可以发现4 次迭代后趋于收敛。这充分表明了所提算法的有效性。

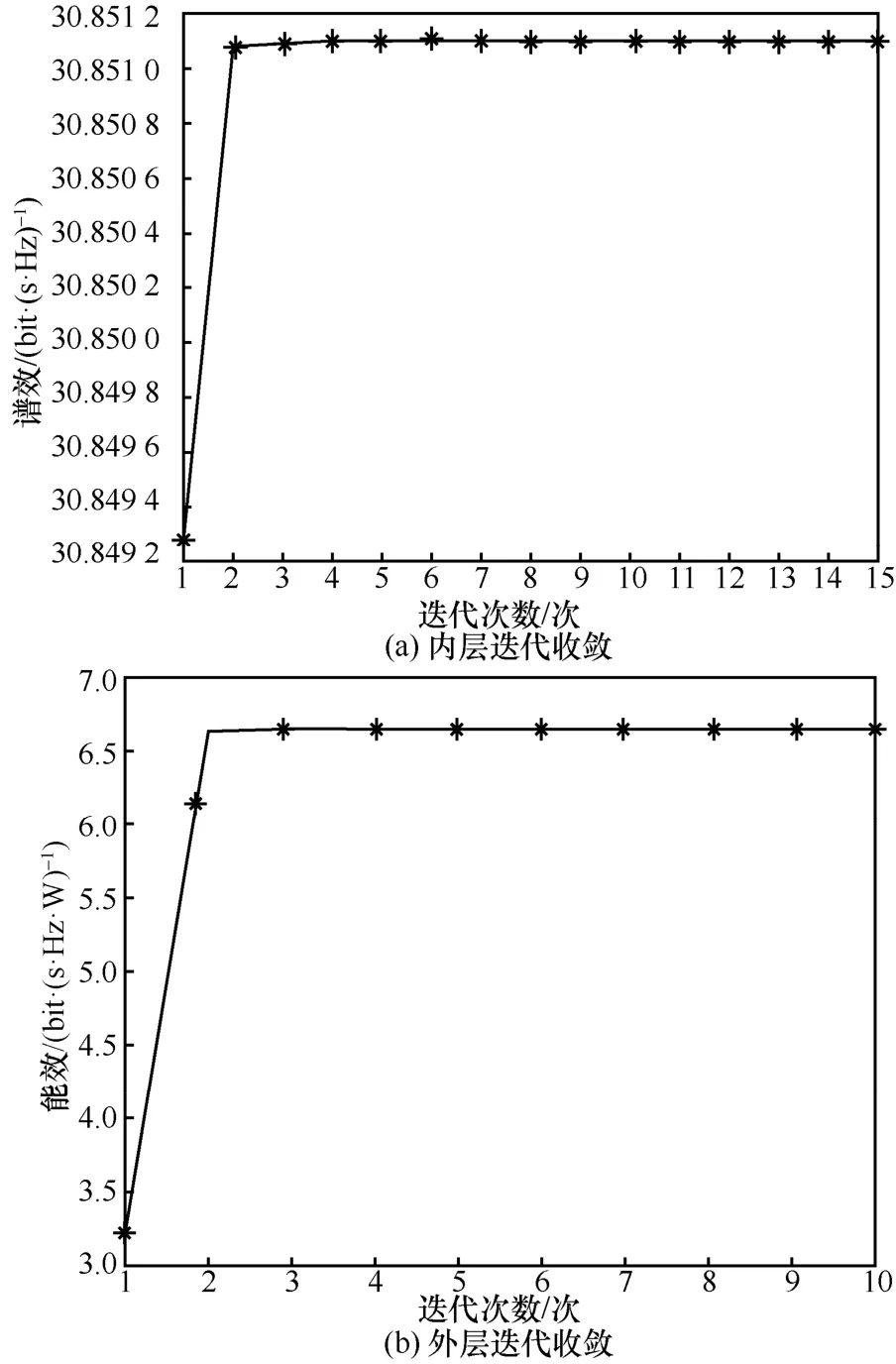
图5 所提算法的收敛性分析

图6 展示了不同连接结构和不同调制网络下，系统谱效和能效与总功率Pmax的关系。图6(a)中计算系统谱效时，令式(22)中η=0，根据算法2 的内层迭代算法进行求解。从图6(a)可以看出，所有方案下系统的谱效均随着Pmax增加而增加。其中，全数字预编码结构下系统的谱效最高，这是因为该结构下每根天线连接唯一的射频链，拥有充分自由度。所提方案下全连接结构的系统谱效优于混合连接和子连接结构。此外，在图6(a)中还可以发现，所提方案下全连接和子连接混合预编码结构的系统谱效均高于传统基于移相器的全连接和子连接结构的系统谱效。

从图6(b)中可以看出，在总功率Pmax较小时，所有方案下系统的能效均随着Pmax增加而增加。与图6(a)不同的是，全数字预编码结构下系统的能效最低，这是由于大量高功耗的射频链导致系统功耗增加。当Pmax≥28 dBm 时，系统能效趋于稳定，这是因为当总功率Pmax较小时，系统能效取决于系统的可达速率；而当Pmax到达30 dBm 后，用户速率的增加无法补偿总功率的消耗。另外，所提方案下系统的子连接结构能效优于混合连接和全连接结构，这与图6(a)中连接结构与系统谱效的关系相反。因此，可以根据对谱效和能效的实际需求选择连接结构。此外可以发现，所提方案的系统能效也均优于传统基于移相器和全数字预编码结构的系统能效。

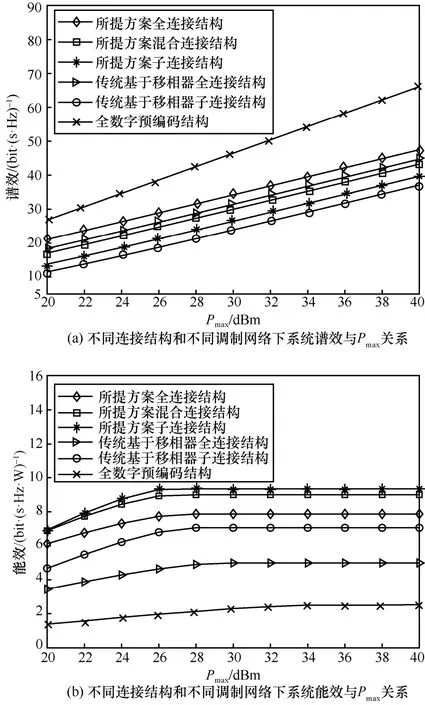
图6 不同连接结构和不同调制网络下系统的能效和谱效与总功率Pmax 关系

设Pmax=30 dBm，不同连接结构和不同网络下系统谱效和能效与天线数的关系如图7 所示。从图7(a)中可以看出，所有方案下系统的谱效都随着天线数的增加而增长。这是因为当天线增多时，天线的阵列增益将变大。此外，从图7(a)中也可以发现，全连接结构的系统谱效优于混合连接和子连接结构，所提方案的系统谱效优于传统基于移相器的系统谱效。

从图7(b)中可以看出，所有方案下系统的能效都随着天线数的增加而降低。这是因为当天线增多时，所需的调制网络器件增多，导致更多的能量消耗，因此许多文献都采用典型的天线数量NTX=64。此外，从图7(b)中也可以发现，子连接结构的系统能效优于混合连接和全连接结构，所提方案的系统能效优于传统基于移相器的系统能效。

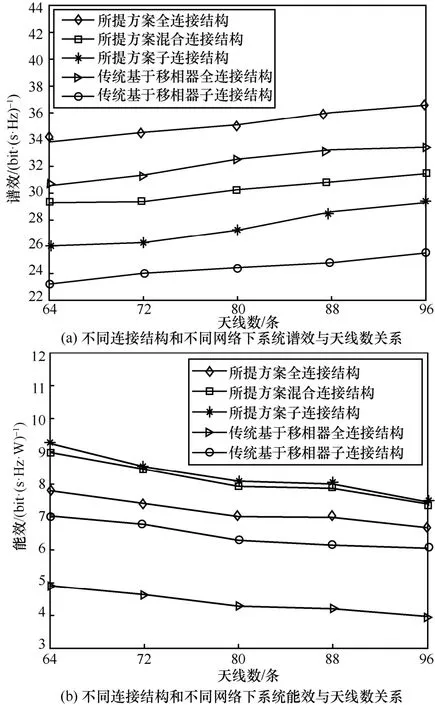
图7 不同连接结构和不同网络下系统的能效和谱效与天线数关系

不同方案下系统的谱效和能效与总功率的关系如图8 所示。从图6 和图7 可以发现当m=2 时，即天线和射频链之间采用混合连接时，系统在频谱和能效方面可以达到一个更好的平衡关系，因此在图8(a)和8(b)的仿真中，设置m=2。其中，MaxEE表示系统能效最大化，而MaxSE 表示系统谱效最大化，即式(22)中η=0。本文的OMA 方案采用的是频分多址接入（FDMA,frequency division multiple access）技术[10]。从图8(a)中可以看出，当总功率Pmax≤26 dBm 时，MaxEE 和MaxSE 的谱效相同，当Pmax＞26 dBm 时，MaxEE 的谱效增速变慢并最终稳定在峰值保持不变。而MaxSE 的谱效随着总功率的增加而增加，这是因为对于MaxSE，系统为了最大化谱效，将总功率分配给了所有的用户。在图8(a)中还可以发现，与OMA 方案相比，NOMA 传输技术可以实现更高的谱效。

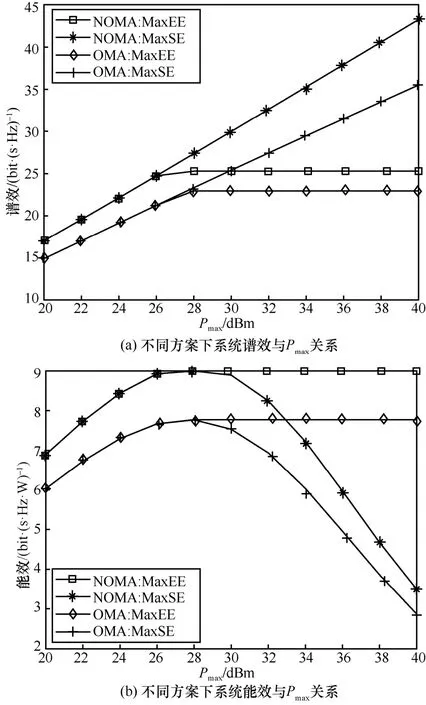
图8 不同方案下系统的能效和谱效与总功率Pmax 关系

从图8(b)可以看出，Pmax为26～28 dBm 时，MaxSE 和MaxEE 的能效增加均变缓，当发射总功率Pmax＞28 dBm 时，MaxSE 能效降低，MaxEE 能效趋于稳定。此外，在能效方面，NOMA 传输技术也是优于OMA 方案的。

图9 展示了不同用户分组方案下系统能效与总功率的关系。可以看出，本文所提改进K-means 用户分组算法性能是最优的。K-means 用户分组算法[11]虽然可以根据信道的状态信息较好地完成用户分组，但其初始簇头的随机性将会影响算法收敛性和系统性能。另外，随机分组算法的性能最差，这是因为NOMA 系统存在用户干扰，而随机分组将会使同一簇内的用户干扰增大。

图9 不同用户分组方案下系统能效与总功率Pmax 关系

5 结束语

本文将NOMA 技术与基于时延线阵列的毫米波系统相结合，研究其能效和谱效最大化问题。其中混合模拟数字预编码设计方面考虑了全连接、混合连接和子连接3 种结构。在完成用户分组和混合预编码设计之后，形成了一个优化功率分配的能效最大化问题。针对该非凸问题，提出一种两层迭代优化算法求得原问题的解。仿真结果表明，与基于时延线阵列的毫米波OMA 系统相比，所提方案在能效和谱效方面均可以获得更好的性能。与传统基于移相器的毫米波NOMA 系统相比，所提方案的系统能效和谱效分别提高32.3%和10.7%。并且通过对比所提方案下3 种不同连接结构的能效和谱效发现，全连接结构谱效最优，子连接结构能效最优，而混合连接结构可以更好地权衡系统谱效和能效。