方形桥墩紊动特性及尾涡区尺寸PIV试验
2022-07-10王茂枚
刘 洋,徐 毅,王茂枚,赵 钢,王 远
(1.江苏省水利科学研究院,江苏 南京 210017; 2.江阴市水利工程公司,江苏 江阴 214400)
桥墩局部冲刷一直以来是水利、水运工程关注的热点问题,大量学者对此开展了研究。例如:王飞等[1]采用FLUENT的自定义函数功能和动网格更新技术,实现了桥墩冲刷过程的可视化模拟,并对圆柱形、尖角形和流线形桥墩的冲刷特性进行了分析;潘志刚等[2]基于支持向量机(SVM)构建了圆形桥墩(以下简称圆墩)局部冲刷深度预测模型,模型预测值与试验值吻合良好。桥墩紊动特性与尾涡区尺寸直接关系到涉水桥梁局部冲刷、水流力计算等一系列工程实际问题,钟亮等[3-4]研究指出,桥梁局部冲刷问题与水流绕桥墩流动而产生的复杂三维紊动特性密切相关,而杨万理等[5-8]研究表明,桥墩所受绕流阻力与墩后尾涡区尺寸之间存在密切关系,因此,针对桥墩紊动特性和尾涡区尺寸的研究均具有重要现实意义。
长期以来,关于桥墩绕流的研究主要以圆墩为原型,方形桥墩(以下简称方墩)绕流水动力特性的研究相对较少。然而,方形作为桥墩结构的一种重要截面形式,由于其工程量小、施工简单,在实际工程中得到较为广泛的应用,在跨长江桥梁中也大量采用,如四川泸州长江大桥等[9]。Tseng等[10]研究发现方墩与圆墩周围水流结构类似,桥墩附近均具有复杂的三维紊动特性,墩前有下降流和马蹄涡,墩后有周期性漩涡运动,但两者在流动细节上有明显的不同。Das等[11]采用声学多普勒测速仪对方墩与圆墩冲刷坑内的马蹄涡结构进行了测量,并比较了两者冲刷坑内墩前马蹄涡的不同特点。Thanh等[12]对方墩局部冲刷特征进行了研究,结果表明方墩的最大冲刷深度发生在墩前角点附近,同时指出采用泥沙输运与床面形态流动模型(FSUM)可以较好地模拟墩柱绕流水流及冲刷特征。梁发云等[13]进一步考虑体型效应对砂土中沉井基础局部冲刷形态的影响,开展了波流水槽模型试验,得出圆形沉井最大冲刷深度和冲刷范围分别位于迎水侧和背水侧的45°范围附近,而方形沉井的冲刷主要发生在方形角点附近的结论。此外,针对方墩所受绕流阻力的研究也取得了一定成果。例如:邓绍云等[14-15]针对前人测量技术的缺陷,设计了专门的测力设备对方墩所受绕流阻力进行了试验测量,得出了各级雷诺数下的阻力系数;Yang等[6-7]和邓斌等[8]类比阿基米德原理对桥墩所受绕流阻力与尾涡区之间的关系进行了初步探究,结果表明方墩所受的绕流阻力与尾涡区体积之间具有较好的线性关系。上述研究主要针对方墩三维绕流流场特性和所受绕流阻力特性,未专门对桥墩周围紊动特性和尾涡区尺寸进行研究。
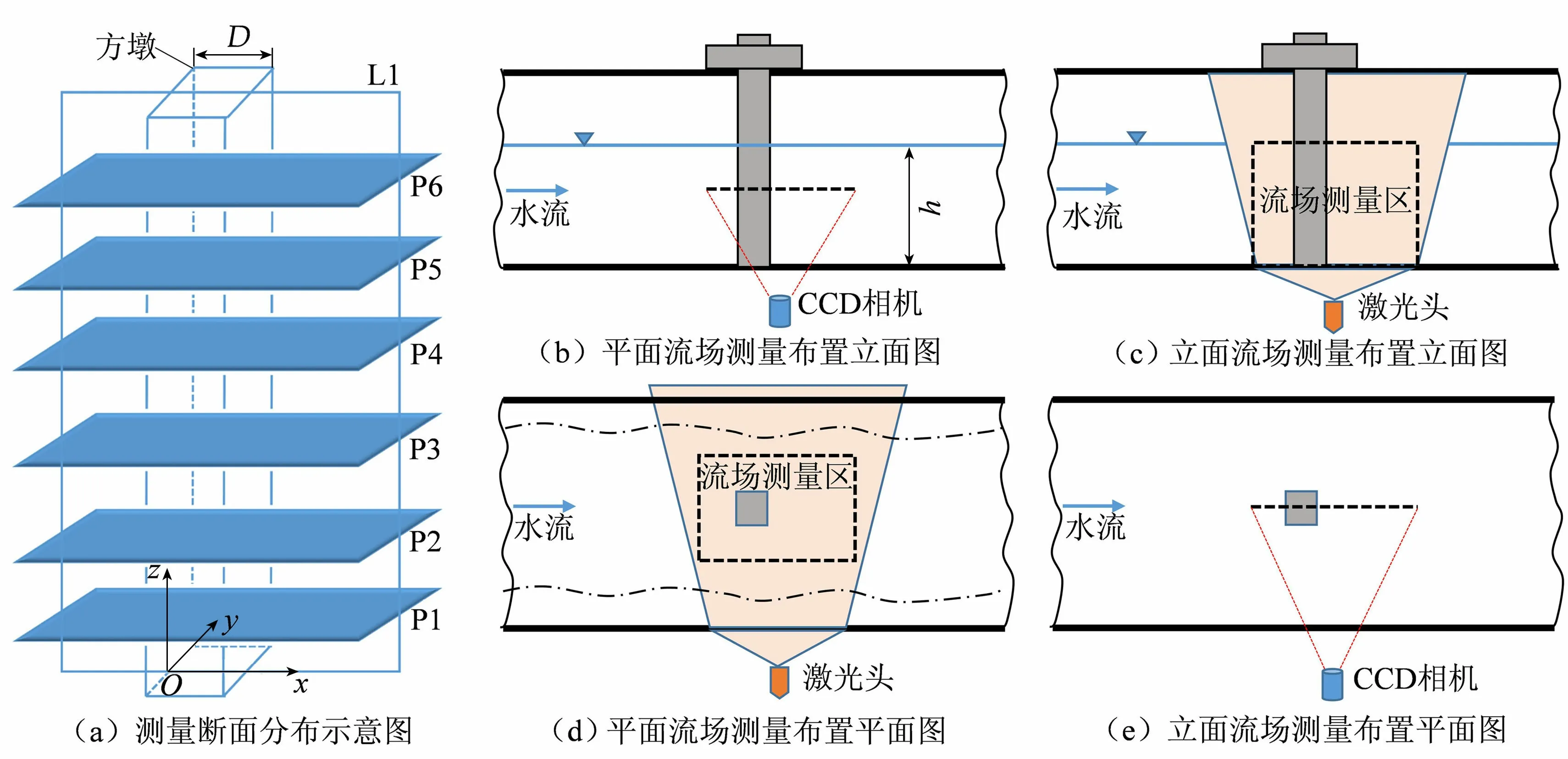
图1 PIV流场测量断面分布及测量布置
为了解方墩周围紊动特性和墩后尾涡区尺寸规律,本文基于粒子图像测速(particle image velocimetry,PIV)技术,对方墩附近紊动特性及墩后尾涡区尺寸进行试验研究,并拟合得到了方墩紊流宽度和墩后尾涡区相对时均体积与弗劳德数的关系式,以及墩后尾涡区相对时均面积与相对水深和弗劳德数的关系式,可为该类水工建筑物的设计和施工提供参考。
1 试验方法
1.1 水槽试验
PIV流场测量断面分布及测量布置如图1所示(图中P1~P6为PIV的xOy平面流场测量断面,L1为xOz立面流场测量断面),试验仪器和坐标系的建立参见文献[8]。根据以往河工模型试验的成功经验[5],本文以边长为5 m的中等尺度方墩为研究对象,淹没水深为20 m,水体流速为1.5~4 m/s,采用1∶100的缩尺比,依据重力相似准则,确定方墩模型边长D=0.05 m,模型淹没试验水深h=0.20 m,试验断面平均流速v控制在0.15~0.40 m/s。为获得多组试验数据以便进行较为系统的分析,设计试验工况6组,相应雷诺数Re为7 500~20 000,弗劳德数Fr为0.107~0.286,试验时保持各组工况水槽底坡i=0.002 5不变,水流工况见表1。
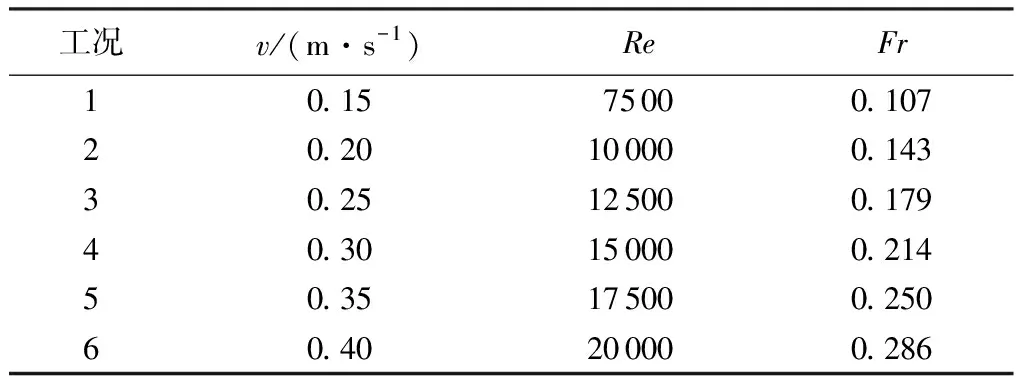
表1 水流工况
试验开始前,利用流速剖面仪(ADCP)检查水槽边壁对试验结果的影响,检查结果表明水槽边壁对试验测试区无明显影响[8]。同时,为验证PIV测量数据的可靠性,在无墩与有墩两种情况下,分别采用ADCP和PIV对同一测线(无墩条件测线位于x/D=0、y/D=0处;有墩条件测线位于x/D=-1、y/D=0或x/D=3.5、y/D=0处)进行流速测量,并将时均处理后的流速数据进行对比,结果如图2所示,可见两种情况下两者测出的流速数据均吻合良好,说明采用本PIV系统测量流场信息具有较高的准确性。
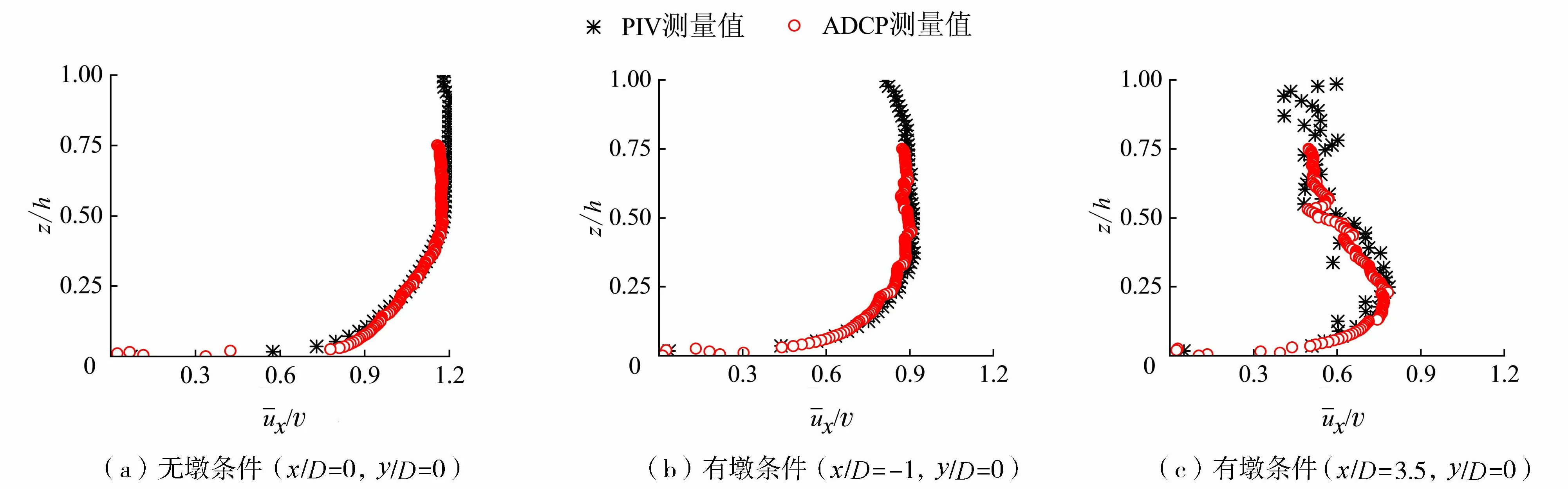
图2 PIV流场测量准确性验证(Re=12 500)
1.2 参数计算方法
为便于对方墩附近紊动特性进行分析,参考文献[3],采用各工况的摩阻流速u*对紊动参数绝对值进行无量纲化处理。各参数计算公式如下:
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
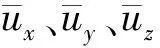
2 试验结果与分析
2.1 方墩附近平面紊动特性
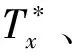
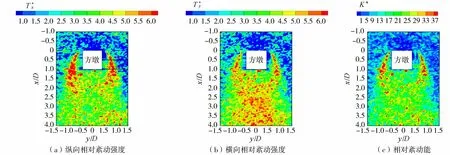
图3 方墩附近紊动参数分布云图(Re=15 000,z/h=0.5)
为进一步对比分析不同雷诺数下方墩两侧紊动参数的分布规律,图4给出了不同雷诺数下3个紊动参数沿特征线T1和T2(特征线见图3,T1线、T2线分别为方墩左侧x/D=0.5和x/D=1.0的水平线)的分布,可以看出,3个紊动参数沿两条特征线分布的总体趋势一致,墩侧水流紊动强度沿横向先从桥墩侧壁的零附近增大一定距离后至极大值,然后迅速减小至零附近,而在墩侧小范围回流区内紊动并不十分强烈;3个紊动参数沿T2线分布的数值大小总体大于沿T1线的分布,说明在墩侧,紊动强度沿水流方向逐渐增大;随着雷诺数的增大,沿两条特征线分布的紊动参数数值逐渐增大,并且极大值逐渐向远离桥墩侧壁的方向推移,说明随着雷诺数的增大,墩侧水流紊动的影响范围进一步扩大。
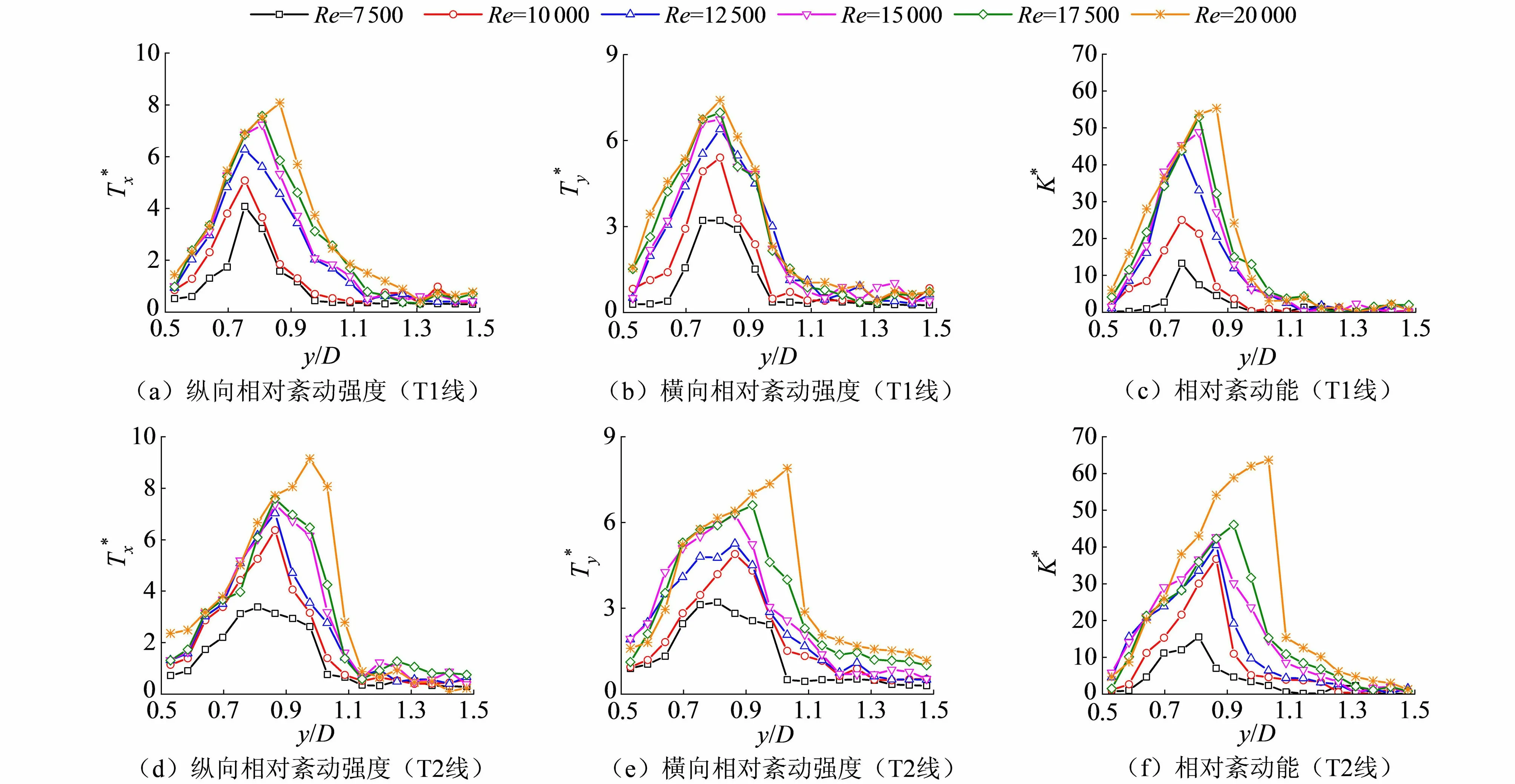
图4 紊动参数沿特征线分布
2.2 方墩紊流宽度分析
前人对于紊流宽度的定义有所差异,李鹤高等[16]以横向流速0.3 m/s为界确定圆墩紊流宽度的范围;沈小雄等[17-18]以横向流速消失点为界确定圆墩的紊流宽度范围,认为桥区水域影响船舶操纵安全和桥梁净宽尺度的水流主要是横向水流;胡旭跃等[19]从紊动强度的角度出发,以桥墩附近总紊动强度极大值出现位置为界确定圆端形桥墩紊流宽度。本文从紊动能的角度出发,将桥墩附近紊动能从极大值减小至较小值(K*=5 )的位置离桥墩纵向中轴线的距离定义为单侧桥墩紊流宽度,两侧桥墩紊流宽度记为B。依据紊动特性试验成果,可得出桥墩相对紊流宽度(B/D)。
图5为不同研究得到的桥墩相对紊流宽度随弗劳德数变化的对比图。由图5可知,沈小雄等[17]和魏彭林等[18]的研究结果变化趋势相似,但魏彭林等[18]的研究结果相对偏小。沈小雄等[17]采用PIV试验测量直槽中圆柱周围近区表层的速度分布,试验时Fr=0.14~0.38,并基于此得到了水流表层紊流宽度与Fr的相关关系。魏彭林等[18]采用格子Boltzmann方法模拟直槽中圆墩三维紊流流场,模拟时Fr=0.14~0.50,并以0.85h水层为研究对象,得出紊流宽度与Fr的关系。由于采用的研究方法不同,且基于的水层不同,沈小雄等[17]是基于水流表层,而水流表层紊动宽度相较其他水层或有偏大,这可能是造成两者计算结果差距较大、魏彭林等[18]计算结果相对偏小的原因。本文方墩的紊流宽度实测值较沈小雄等[17]和魏彭林等[18]圆墩的计算值整体偏大,说明方墩紊流宽度相应要大于圆墩紊流宽度。随着弗劳德数的增大,紊流宽度逐渐增大,这是由于随着弗劳德数的增大,导致桥墩两侧及墩尾涡量相应增大,桥墩两侧水流方向变化范围随之扩大而造成的。
由以上分析可知,顺直河道中桥墩紊流宽度主要与桥墩尺度、弗劳德数等参数有关。利用实测数据拟合得到相对紊流宽度与弗劳德数的关系式(式(9)),相关系数达到0.99,相关性良好,说明方墩相对紊流宽度与弗劳德数存在较好的幂函数关系,如图5所示。
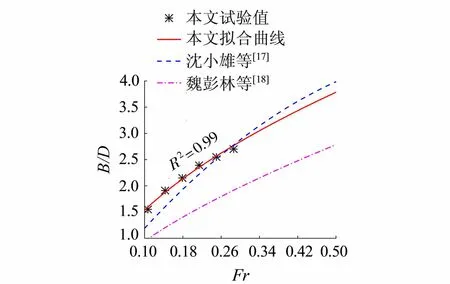
图5 相对紊流宽度随弗劳德数的变化
B/D=5.58Fr0.56
(9)
2.3 墩后尾涡区面积变化规律
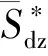
图6为不同弗劳德数下墩后尾涡区相对时均面积沿相对水深(z/h)分布对比图。由图6可知,同一水深位置处的尾涡区相对时均面积随弗劳德数的增大而增大;而同一弗劳德数下,尾涡区相对时均面积沿水深方向(z轴正向)先增大后减小,这是由于水槽底部边界层和墩后自由液面下降共同作用的结果;同时,随着弗劳德数的增大,墩后尾涡区相对时均面积沿水深方向由增大转为减小的拐点总体上向远离自由液面的方向移动,这是由于随着弗劳德数的增大,墩后自由液面向下波动更为剧烈,对尾涡的形成产生更为强烈的影响造成的。利用不同弗劳德数下墩后尾涡区相对时均面积随相对水深变化的实测数据,拟合得到尾涡区相对时均面积与相对水深和弗劳德数的关系式(式(10)),相关系数达到0.938 5,相关性良好,如图7所示。
(10)
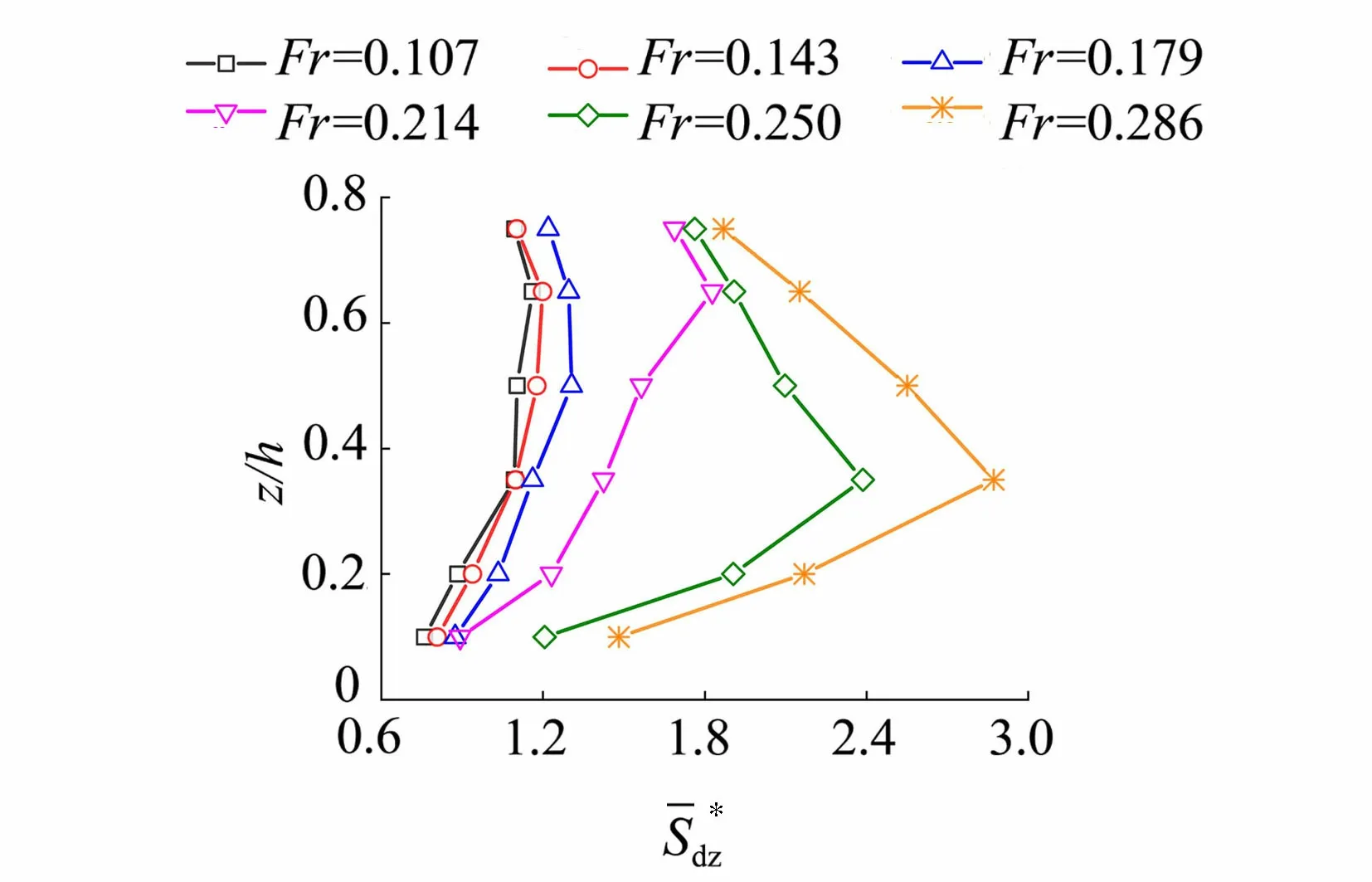
图6 墩后尾涡区相对时均面积沿相对水深的分布
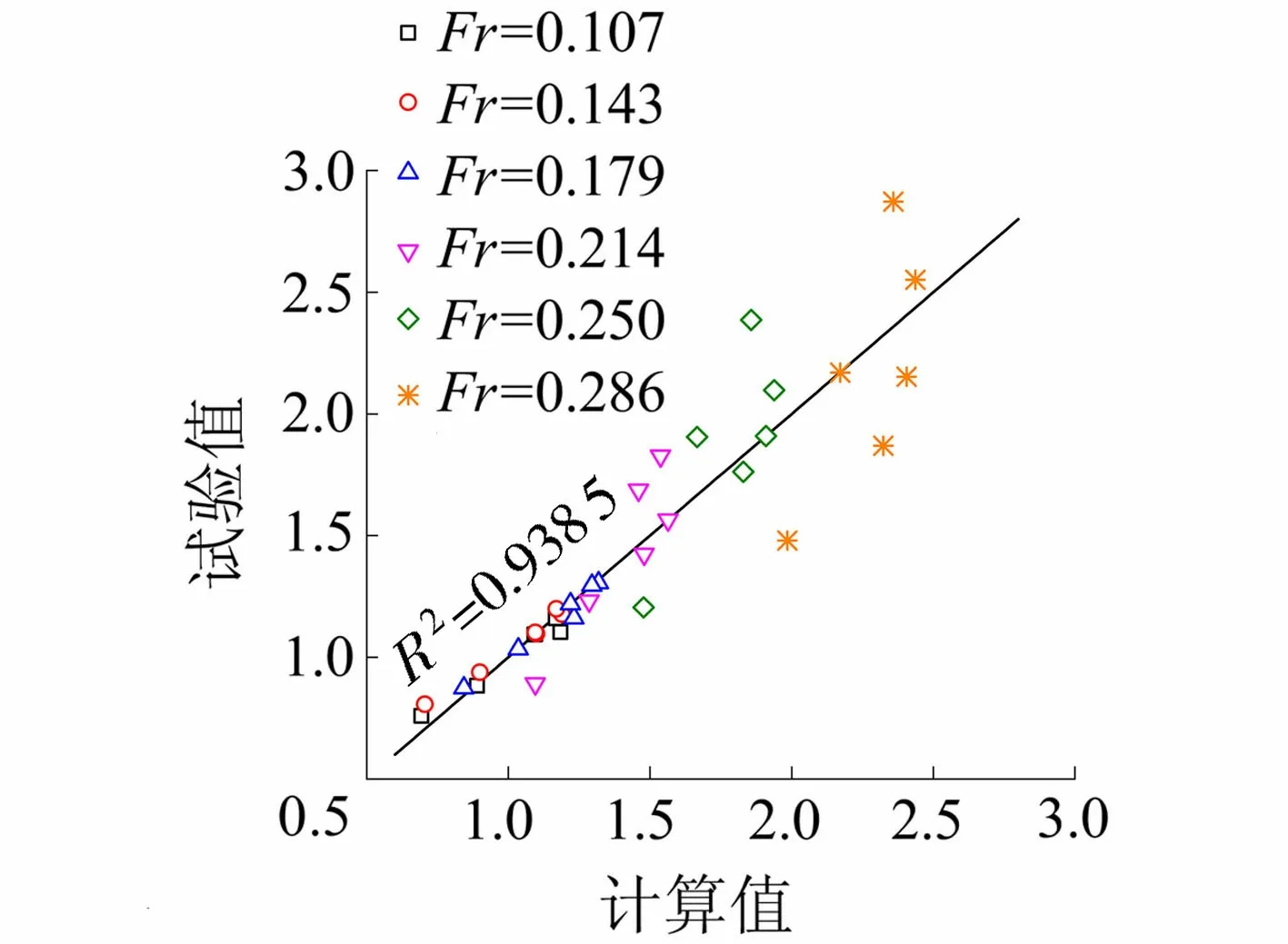
图7 尾涡区相对时均面积与相对水深和弗劳德数的关系
2.4 墩后尾涡区体积变化规律
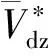
(11)
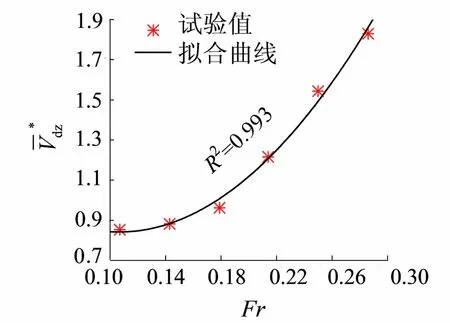
图8 尾涡区相对时均体积随弗劳德数的变化
3 结 论
a.方墩迎流角点两侧出现较大紊动强度分布,并呈现出包裹方墩的“喇叭”形状向下游逐渐舒展扩大;墩侧紊动强度沿横向先增大至极大值,而后迅速减小至零附近,紊动强度极大值往往发生在背流角点两侧附近,而两侧及墩后回流区内紊动并不十分强烈;随着雷诺数的增大,墩侧水流紊动的影响范围逐渐扩大。
b.从紊动能的角度出发,定义桥墩紊流宽度,并根据实测数据拟合出相对紊流宽度与弗劳德数的关系式,发现相对紊流宽度与弗劳德数存在较好的幂函数关系,相关系数达到0.99,相关性良好。
c.根据实测数据,拟合出墩后尾涡区相对时均面积与相对水深和弗劳德数的关系式,相关系数达到0.938 5,相关性良好;同时,拟合得到墩后尾涡区相对时均体积与弗劳德数的关系式,发现尾涡区相对时均体积与弗劳德数存在较好的二次函数关系,相关系数达到0.993,相关性良好。
