考虑橡胶坝影响的水动力学模型
2022-07-10刘恒光郝瑞霞何晓燕胡孜军
刘恒光,郝瑞霞,何晓燕,胡孜军
(1.太原理工大学水利科学与工程学院,山西 太原 030024; 2.中国水利水电科学研究院,北京 100038;3.水利部防洪抗旱减灾工程技术研究中心,北京 100038)
橡胶坝具有美化城市景观等功能。近年来许多城区河道建设了橡胶坝。水流在河道及河漫滩的演进过程可用水动力模型模拟[1-3],但橡胶坝对河道行洪具有复杂的阻水影响,给含橡胶坝河道的洪水演进数值模拟带来了困难。考虑橡胶坝影响的水动力学模型可以有效地预测河道水流过程,模拟河网中复杂水利工程的调度和控制,对刻画水位、流量等水力要素的时空变化具有重要的实用价值,能够为相关部门提供科学精准的技术支撑,对保障流域经济社会平稳发展具有重要意义[4]。
目前已有很多学者开展了闸堰影响下的水流数值模拟研究。例如:Feng等[5]建立了一种洪水演算方法,提出在闸堰调控的多分支河网中建立虚设单元河段,然后采用双追赶方法求解;姜恒志等[6]采用泰勒级数展开法,进行堰出流的模拟,建立了具有内部边界堰存在时的河网非恒定流水动力学模型;施勇等[7]提出了基于水动力学的闸坝调度计算格式并应用于长江中下游防洪系统;张晓波等[8]利用替代法处理过闸流量并模拟了河网闸堰过流和调度影响;李大鸣等[9]考虑河网中复杂的水闸控制条件,提出了双向迭代内边界控制法,对具有闸堰的特殊河段进行数值模拟;吴松柏等[10]提出了改进双向迭代内边界法求解含闸堰方程,并应用于多闸联合调度方案的数值模拟,可以有效模拟河网地区的闸堰过流和调度影响;刘芹等[11]全面比较了对闸堰过流能力公式线性化处理的泰勒法和替代法两种计算方法,得出替代法具有处理方式更便捷、计算公式更简洁、更易程序化的优点,在河网模型中可优先采用;陈炼钢等[12]根据已知的闸坝运行水位流量资料、调度规则和设计参数等内边界条件给出了闸堰所在河道断面的追赶系数,进行了闸坝调度过程模拟;杨甜甜等[13]为提高洪水预报精度建立了水文水动力耦合模型,但未考虑汛期遇洪水时研究流域内橡胶坝等工程对河道洪水演进过程中水位和流量等水力参数的时空变化影响。可见,关于橡胶坝运行过程对河网水流运动影响的相关研究较少,专门考虑橡胶坝内边界条件的河网水动力学模型并不多见,需要展开深入研究。
汛期橡胶坝与普通闸堰在实际运用过程中有一定的差别,通常在大量蓄水后开始运用橡胶坝,然后橡胶坝逐渐降坝,直至完全塌坝。本文构建考虑橡胶坝的不同过流情况的一维水动力学模型,并将该模型应用于淠河流域干流下龙爪到隐贤集河段,对近年来淠河发生的实测典型洪水过程进行模拟验证,对橡胶坝不同运行工况进行数值模拟,并对计算结果进行对比分析。
1 控制方程与数值方法
1.1 控制方程
一维河道水动力学计算采用圣维南方程组,其连续性方程和动力方程形式如下:
(1)
(2)
式中:B为过水断面宽度;Z为断面水位;t为时间;Q为过水断面平均流量;x为空间坐标;q为单宽旁侧入流;α为动能校正系数;A为过水断面面积;g为重力加速度;C为谢才系数;R为水力半径。
1.2 控制方程的离散与数值计算方法
采用Preissmann四点隐式差分格式离散方程(1)(2)并作线性化处理,得到任一河段的差分方程为
(3)
(4)
忽略n+1,式(3)(4)可写为
Qj+1-Qj+CjZj+1+CjZj=Dj
(5)
EjQj+GjQj+1+FjZj+1-FjZj=Φj
(6)
式中:上标n与下标j分别为时间与空间步数;Cj、Dj、Ej、Fj、Gj、Φj为计算系数,均由初值计算,具体见参考文献[14]。
一维河网非恒定流水力计算的关键在于汊点水力要素的求解,本文采用河网三级联解法[14]对河网模型进行求解。基本思路为:①将河网中两节点间的河道划分为若干小河段,在计算断面上对圣维南方程组进行有限差分计算,离散后得到河道各断面水位、流量的差分方程组;②对方程组进行自消元,形成河道首末断面的流量与水位之间的线性关系;③根据汊点的水量平衡关系得到汊点水位方程组,求解该方程组可计算出各汊点的水位值;④根据各汊点水位值回代求解各河道断面的水位和流量。
2 含有橡胶坝的特殊河段处理方法
在河道上布置闸坝等水工建筑物,会使河道上出现几何形状或水力特性的间断点,河道水流不再具有连续性[14]。因此,传统的圣维南方程组不再适用于此类复杂河网,必须根据其水力特性进行特殊处理。而汛期橡胶坝是一类具有复杂水利工程调度规则的挡水建筑物,需要合理、科学地在这类特殊河段上考虑橡胶坝的内在调度运行方式,并保证水流运动计算的连续性和稳定性。
2.1 橡胶坝数值模拟计算流程
水动力学模型橡胶坝数值模拟计算分为控制对象、控制条件、控制目标3个部分。控制对象是一个或者多个实际工程控制对象(如单级橡胶坝或梯级橡胶坝等),汛期橡胶坝调度控制起始条件是基于实际的水利工程调度运用规则确定的,常用的规则包括坝上水位与坝顶最高高程的水位差、区间降水量与上游水库是否超过汛限水位、水利工程出流量、关注点水位及流量、多组条件综合等,进而达到设定的控制目标(如调节橡胶坝的塌坝速度,延时控制时间等),最终形成完整的橡胶坝数值模拟计算流程。
当模型需要精细化模拟含有橡胶坝河段的洪水演进过程时,模型进入橡胶坝模块,根据计算流程中的判断条件判定是否开始塌坝,结合工程实际情况给模型设计一个合理的塌坝速度并均匀降坝,坝高在每个时间步长内线性地降低,使橡胶坝在上游洪水到达坝址前完成降坝。确保模型的运行逻辑与实际工程安全运行下的情形相一致。模型计算出当前时刻含有橡胶坝河段的追赶方程,联合河网方程组,完成求解。当前时刻计算完成后,进行下一时刻的计算,迭代直至整个计算历时完成。
图1为橡胶坝模块数值模拟计算流程图。在实际工程中,由于橡胶坝通过排出坝袋中的水来实现塌坝泄流,随着坝高的降低,坝顶宽度逐渐增加,坝袋形状由最初的实用堰型塌至近似于宽顶堰型[15]。所以在设计模型时,橡胶坝在塌坝过程中以实用堰堰型匀速进行控制塌坝,在完全塌坝后以宽顶堰的过流方式进行计算。计算完成后,结束并退出该模块。如果当前时刻的雨水工情不满足橡胶坝模块的判定条件,则说明实际橡胶坝未触发降坝,按照设计坝高的实用堰进行过流计算。
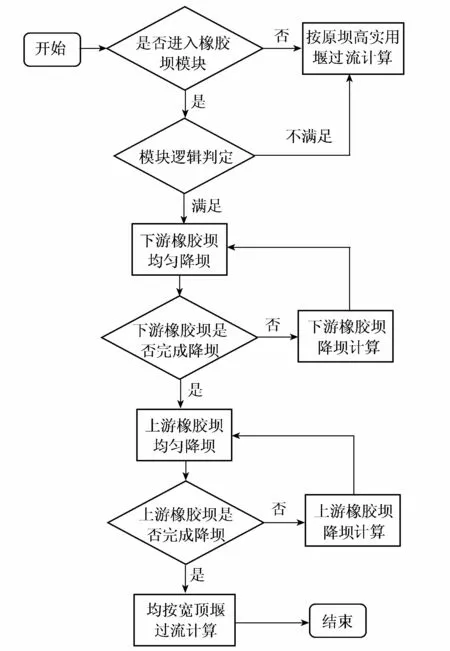
图1 橡胶坝数值模拟计算流程
2.2 含有橡胶坝河段的计算方程
由于过坝水流为急变流,且流态变化十分复杂,模拟的关键技术是如何准确描述堰坝的过流能力和确定计算方程的数值计算格式,使模拟计算稳定,不易发生震荡[12]。一维水动力学模拟中堰坝调控的线性化处理方法主要有泰勒级数展开取一阶项[6]、前时段计算结果近似替代(简称替代法)[8]、转化微分形式[12]、能量方程构建调度计算河段方程[7]以及双向迭代法[9]等。由于替代法的方法处理方式简洁、易于程序化实现,本文采用替代法对含有橡胶坝的特殊河段进行处理。
当流态为自由出流和淹没出流[14]时,过流流量分别为
(7)
式中:Q为过坝流量,m3/s;m为自由出流系数;B为坝宽,m;Zj、Zj+1分别为当前时刻坝上游水位和下游水位,m;Zd为坝顶高程,m;φ为淹没出流系数。
在模型数值模拟计算中,水流流态处于自由出流与淹没出流过渡段时,可能会出现数值异常,产生数值振荡或发散等问题。采用线性插值连接自由出流和淹没出流这两种流态过渡区间段的方法,可以保证流态转换过程中的连续性。经过本文数值模拟验证,采用这种方法,既可以有效提高模型的稳定性,又可以保证模型的精确性。
根据替代法思想[8],在计算时间步长不大的前提下,认为前后两个时段断面的水力要素变化较小,可以利用前一时刻的部分变量替代当前时刻的部分变量,以达到分离未知量的目的,这样的处理方法在文献[8,11]都有应用和验证。
以河道首末断面水位为未知量构建含有橡胶坝计算河段的双追赶方程[17]:
Qj=αj+βjZj+ζjZj+1
(8)
Qj+1=θj+1+ηj+1Zj+1+γjZj
(9)
式中:Qj、Qj+1分别为当前时段含有橡胶坝河段j断面与j+1断面的流量,m3/s;αj、βj、ζj、θj、ηj、γj为式(5)(6)相应的追赶系数。
本文只研究坝的过流在水力计算中的特殊处理,故将过坝流态分为自由出流和淹没出流两大类。推求替代法构建的含有橡胶坝计算河段的追赶系数αj、βj、ζj、θj、ηj、γj,具体计算公式如表1所示。

表1 替代法推导的含有橡胶坝河段的追赶系数计算公式
3 实例验证
3.1 流域概况及模型建立
为检验受汛期橡胶坝调度影响所建立的水动力学模型的稳定性和有效性,选取位于淮河支流淠河流域佛子岭、响洪甸两座水库至迎河集区间作为试验河段,重点研究位于下龙爪站至隐贤集站河段六安城区的六安橡胶坝和六安城北橡胶坝两座串联橡胶坝,如图2所示。
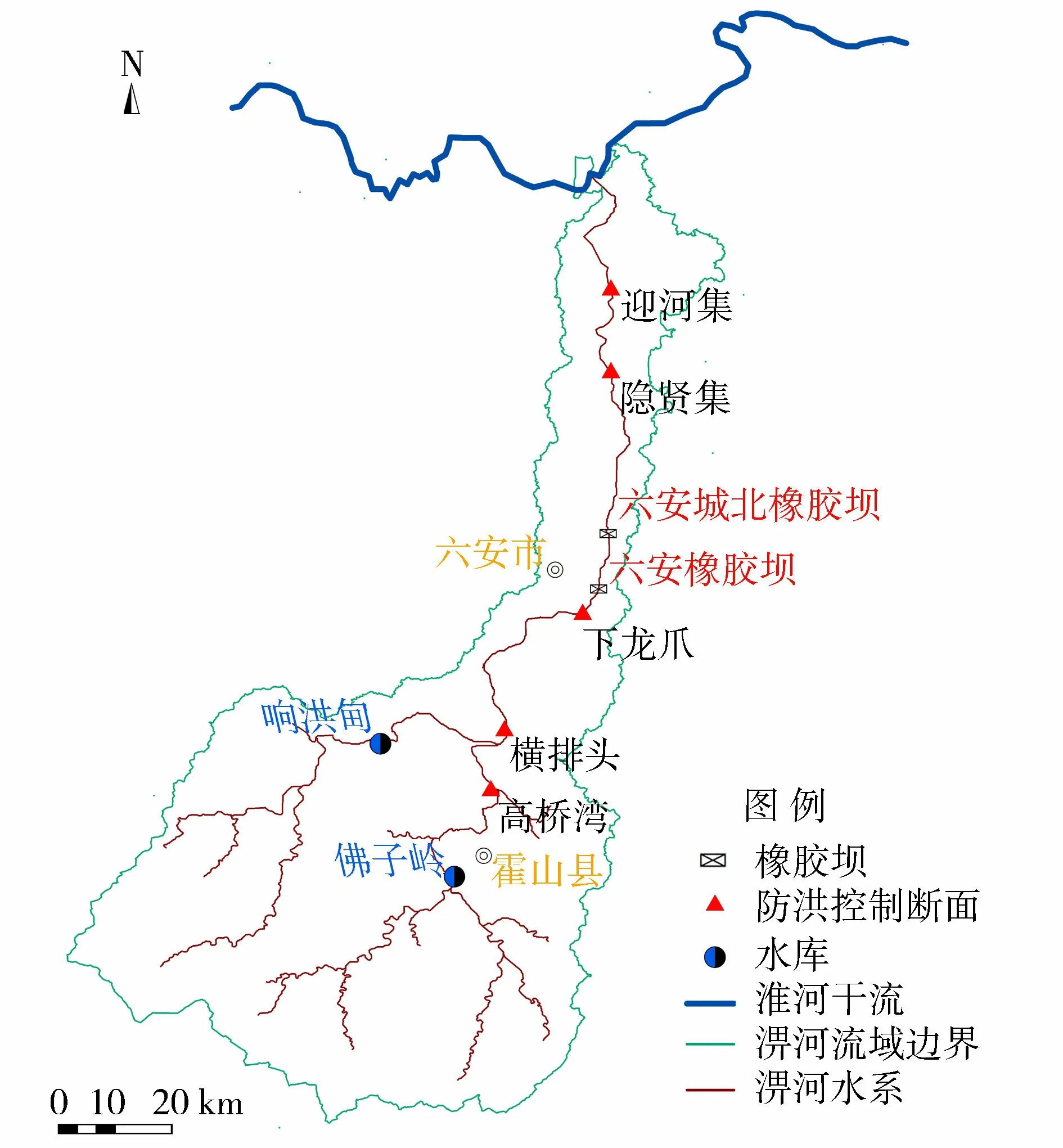
图2 淠河流域研究区域
淠河是淮河中游南岸的一条较大支流,全长260 km,流域面积6 000 km2,是六安市防汛重点河流。六安城区两座橡胶坝对流域防洪安全十分重要。将研究流域整个河道共分为现东淠河河段、西淠河河段、淠河干流上游河段、月亮岛东侧河段、月亮岛西侧河段和淠河干流下游河段等6个河段,其中横排头、下龙爪、隐贤集3站具有实际观测资料。本文采用断面资料为2019年实测地形数据,其中东淠河上有42个断面,西淠河上有31个断面,淠河干流上有86个断面,共159个大断面,断面平均间距约1 km,满足模型计算要求。采用近年来发生的典型历史洪水过程进行演算作为验证,时间步长Δt取200 s,空间步长采用断面间距,由于河道区分滩地和河槽不同地形条件,糙率n的取值范围为0.035~0.050。以响洪甸水库和佛子岭水库的实测调度出库流量作为上边界条件,迎河集站水位流量关系作为下边界条件,在此基础上建立水动力学计算模型进行洪水演算。为有效模拟汛期六安两座橡胶坝受到的影响,在坝上和坝下分别设置上下两个特殊节点作为橡胶坝模块的特殊计算河段。上游六安橡胶坝充满状态时的坝顶高程P1为36.00 m,下游六安城北橡胶坝充满状态时的坝顶高程P2为34.40 m,两座橡胶坝概化图见图3所示。
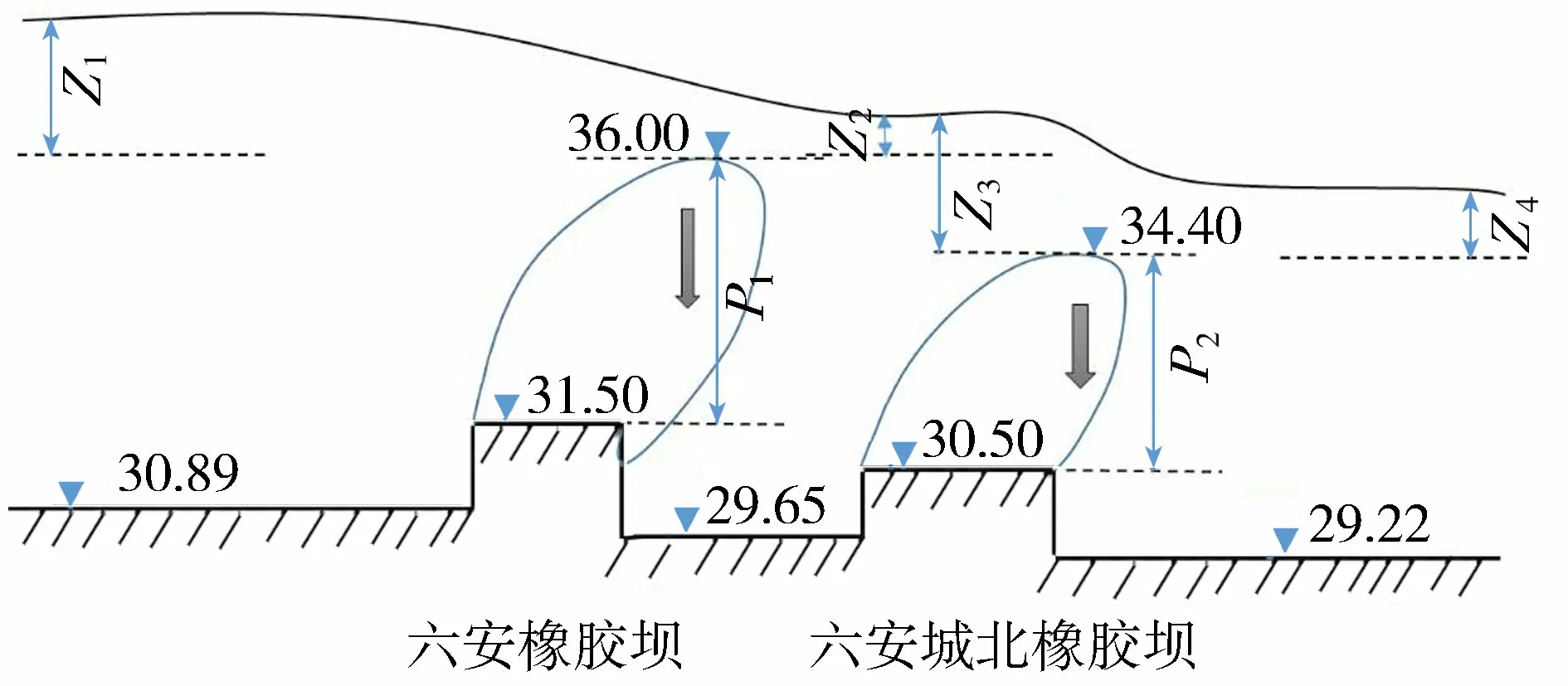
图3 淠河串联橡胶坝概化(单位:m)
根据《六安市淠河城区段橡胶坝群联合运用调度办法》调度运用规则条件及要求,当坝上水位超坝顶最高高程0.3 m,横排头下泄流量达到200 m3/s,横排头至橡胶坝区间降水量达到50 mm,且上游水库超汛限水位,并有大暴雨时串联橡胶坝群进行降坝运用。橡胶坝群自下而上开始逐级泄水,即在上游洪水到来之前,首先泄掉六安城北橡胶坝的蓄水,然后开始泄六安橡胶坝的蓄水。由于上游水库放水到达六安橡胶坝处时间约为2 h,洪水到达坝前时,橡胶坝均已完成降坝。根据两座橡胶坝的实际坝高,计算出模型中两座串联橡胶坝在每个时间步长内的降坝高度达到0.23 m,即降坝速度v至少为0.23/Δt,方可达到实际工程要求。所以设计降坝过程中每个时间步长橡胶坝的坝高会随着时间变化,直至上游洪水到达橡胶坝前,两座橡胶坝已经按照调度运用规则完成塌坝,则两座橡胶坝均按照完全塌坝高度的宽顶堰堰型进行过流计算。综上所述,本模型中的控制对象是六安城区的两座串联橡胶坝。控制条件为同时满足:①橡胶坝群坝上水位大于0.30 m;②横排头下泄流量大于200 m3/s;③横排头至橡胶坝区间降水量大于等于50 mm时。开始执行淠河串联橡胶坝对象组合控制目标,即下游的六安城北橡胶坝开始执行以0.23/Δt的启闭速度匀速降坝,最终控制目标为完全塌落,完全塌落后,按宽顶堰堰型过流计算。上游的六安橡胶坝在达到控制条件时,延迟相应的时间(本文设为3 400 s)再执行塌坝控制,以0.23/Δt的启闭速度匀速降坝,最终控制目标为完全塌落。直至上游橡胶坝降至坝底高程后,也按照宽顶堰堰型过流计算,直至整个计算历时完成。
3.2 情景模拟及结果分析
下龙爪和隐贤集水位站分别位于两座橡胶坝的上游和下游。以2020年淠河流域发生的典型洪水“20200719”为例进行情景模拟,以下龙爪和隐贤集两个水位站的实测资料作为水动力学模型的验证资料,对洪水期间未塌坝运行(情景Ⅰ)和考虑橡胶坝影响(情景Ⅱ)两种情景分别进行数值模拟,通过比较典型洪水不同情景下的数值模拟结果与两个水位站实测资料的拟合程度,进行数据分析。计算结果对比过程线如图4所示,橡胶坝所在断面的模型计算流量和水位过程如图5所示。
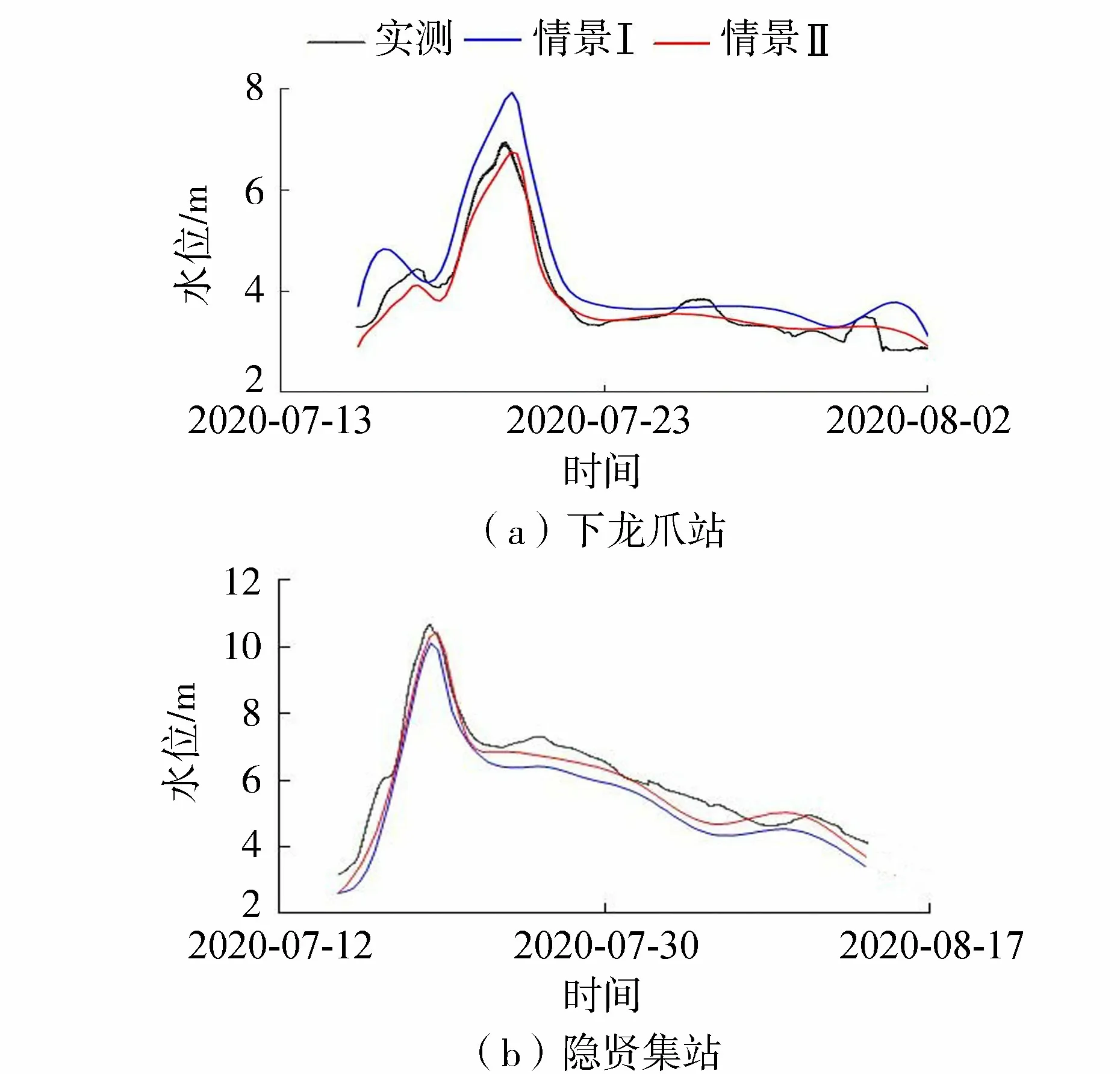
图4 下龙爪站和隐贤集站“20200719”洪水水位模拟过程对比
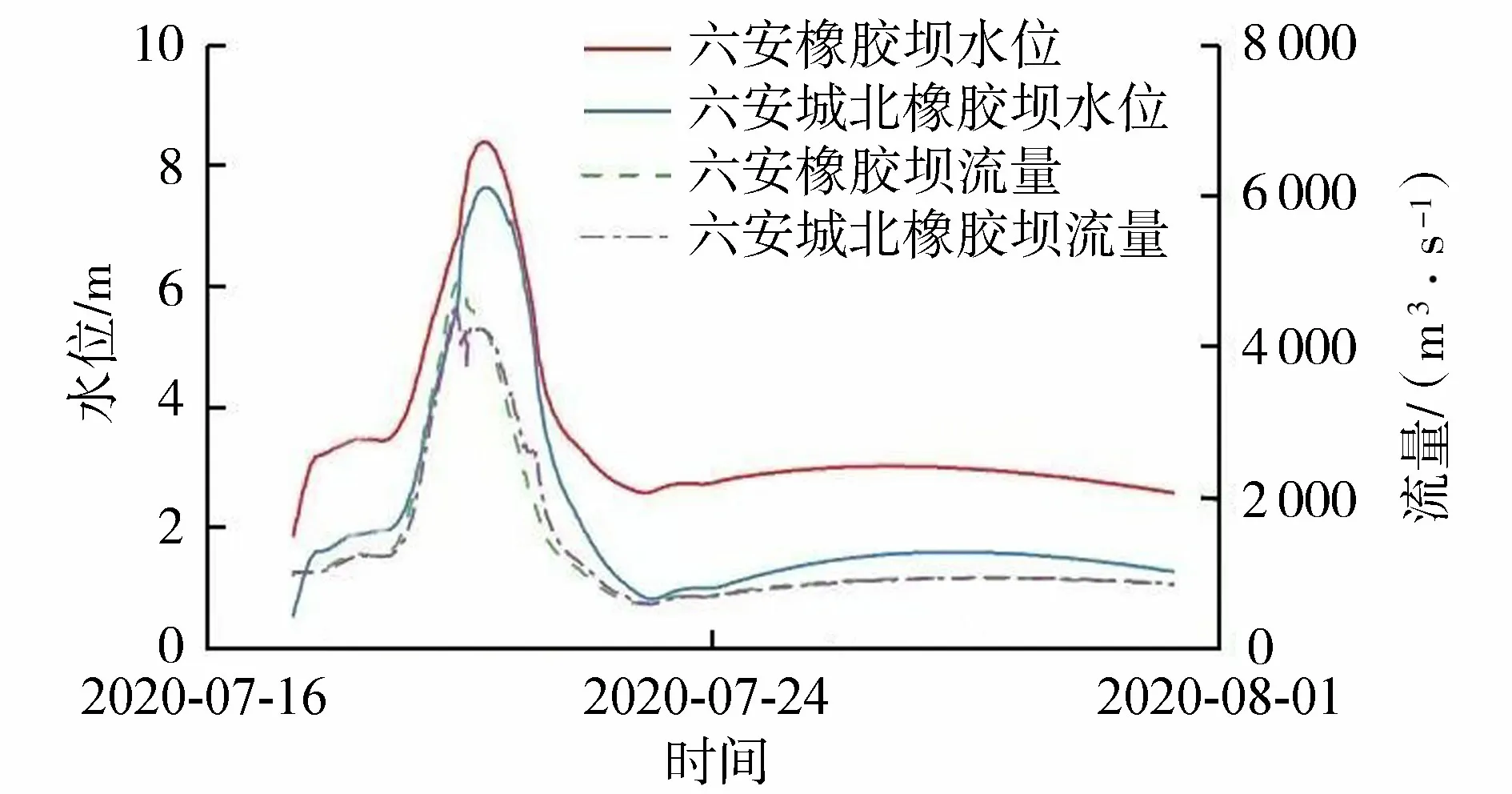
图5 “20200719”洪水橡胶坝所在断面的模型计算流量和水位过程
模型在两种情景下的计算过程中均没有出现不收敛的情况,说明本文构建的水动力学模型算法稳定。情景Ⅱ的计算结果与下龙爪、隐贤集水位站的实测数据拟合程度较高,涨落趋势一致,洪峰水位及峰现时间基本吻合。相较于情景Ⅰ,情景Ⅱ的计算精度得到明显改善。由图4(a)可知,下龙爪站在2020年7月19日22:36水位达到峰值6.94 m,情景Ⅰ计算水位在2020年7月20日0:54出现洪峰水位7.89 m,绝对水位误差为0.95 m,情景Ⅱ计算水位在2020年7月20日0:43出现洪峰水位6.71 m,绝对水位误差为0.23 m;由图4(b)可知,隐贤集站实测水位在2020年7月20日7:18水位达到峰值10.65 m,情景Ⅰ计算水位于2020年7月20日11:33出现洪峰水位9.60 m,绝对水位误差为1.05 m,情景Ⅱ计算水位于2020年7月20日9:47出现洪峰水位10.40 m,绝对水位误差为0.25 m。影响水位精度的主要因素可能是:①淠河下游控制断面的边界条件迎河集水位流量关系不稳定且呈现复杂的绳套关系;②淮河干流的顶托现象对淮河支流淠河下游河道可能造成实测水位比模拟水位偏高,导致计算结果与实测结果有一定误差,但模拟结果整体满足精度要求,具有较高的稳定性和可靠性。
另外选取近年来发生的“20160702”“20180818”和“20200623”3场典型历史洪水进行分情景演算,并用实测水位资料、峰现时间误差进行验证,情景Ⅱ的计算拟合效果均优于情景Ⅰ的拟合效果,将4场典型洪水计算结果整理至表2。由表2可知,情景Ⅱ实测水位与水位计算值相差极小,峰现时间也吻合较好,表明根据本文提出的思路所建立的一维水动力学模型可以较好地模拟含有橡胶坝河段的洪水演进过程。而在实际模拟中,如果对洪水期间橡胶坝塌坝过程考虑较少,导致计算误差较大,对洪水预报精度产生影响。
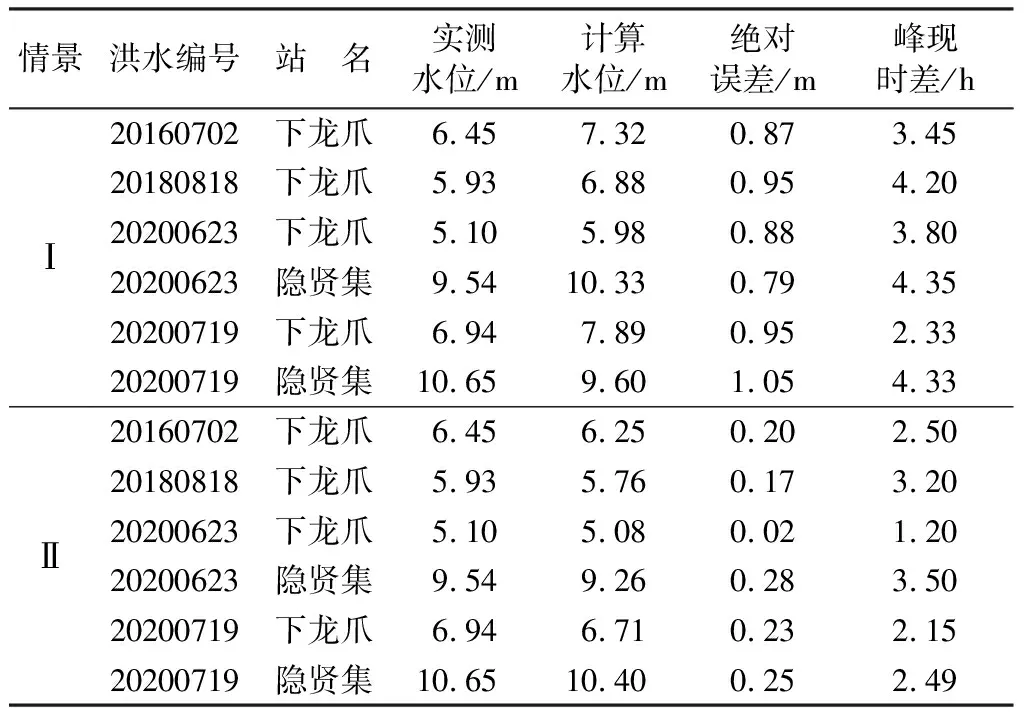
表2 历史典型洪水计算误差
4 结 论
a.在Preissmann四点隐式差分格式离散方法基础上,提出了以橡胶坝作为内边界条件的河网水力计算模型,主要包括含有橡胶坝的特殊河段计算流程和考虑橡胶坝工程过流计算中采用的处理方法等。
b.针对淠河流域下游橡胶坝的运行规则特点,构建淠河流域橡胶坝数值模拟计算流程,通过多年实测水文资料验证,对比洪水期间两种工况下的情景模拟结果可以看出,过于简化考虑橡胶坝运行过程会使计算结果产生较大误差。而考虑橡胶坝影响的水动力学模型可以提高洪水期间的模拟精度,有效模拟含有橡胶坝河段的洪水演进过程。
c.本文采用的模型可以较好地拟合淠河流域的洪水演进过程,可以稳定、精确地模拟六安城区含橡胶坝河段的洪水演进过程,并在淠河流域洪水预报预警调度系统中取得较好的应用效果。可将该模型推广应用于其他含有橡胶坝河段的洪水预报。
