低轨TDICCD相机像质地面模拟测试技术研究
2022-07-10成俊舟胡明鹏王玉龙杨文博
成俊舟,胡明鹏,王玉龙,杨文博
(1.中国科学院光电技术研究所,四川 成都 610209;2.中国科学院大学,北京 100049)
引 言
近年来,遥感技术作为一种重要的地球观测手段,在各个领域愈发起着重要的作用。为了保证特定遥感器在轨工作性能与预期指标相符,需要对其进行充分的地面测试。为此,需要一套时间延迟积分电荷耦合器件(TDICCD)相机地面模拟测试设备。
长春光机所的何煦等[1-2]研制了一套调制传递函数(MTF)测试系统,能够对成像系统的动、静态的传递函数进行测量,其使用的测量方法是鉴别率法,虽然这种方法较为简单、容易实现,但一次只能测量有限点处的MTF,而且需要根据不同的被测系统更换靶标;北京空间机电所的杨沐等[3]搭建了一套面向动中成像工作模式的地面成像试验系统,研究了光强、积分级次等因素对MTF的影响,但该系统没有实现偏流角模拟的功能,且靶标同样是鉴别率靶,具有一定的局限性;西安应用光学研究所的姜昌录等[4]研制了一套光电成像系统动态传递函数测量装置,动态MTF测量范围为 0.10~0.99,测量不确定度为U=0.05(k=2),但是,在这套系统中没有增加对偏流角的模拟功能。
针对以上不足,本文提出了一种用于空间TDICCD相机地面模拟测试的装置,可以对相机在轨时的速高比v/h、偏流角 θ 这两个主要像质影响因素进行模拟。装置采用刃边法进行MTF测量,能够快速、便捷的对系统性能进行评估。理论分析证明其测量精度优于5%,实验验证了其可行性,满足项目需求。
1 理论基础
1.1 TDICCD成像原理
TDICCD成像原理是在相机运动过程中,不同的积分级次分别对同一景物进行成像,最后将各级次的结果累加起来并输出。这种方式相当于增加了积分时间,从而提高了成像质量[5]。从该原理可知,需要不同级次所拍摄的景物保持一致才能保证输出图像的质量。诸如振动、姿态变化等因素都会对这种相机的像质造成影响。本文针对速高比v/h和偏流角 θ (见图1)这两个主要因素对像质造成的影响进行了分析。

图1 速高比(v/h)及偏流角(θ)示意图Fig.1 Schematic diagram of velocity height ratio (v/h) and deflection angle (θ)
1.2 刃边法测量原理
MTF是当前最常用、最核心的相机性能指标。成像系统可以被看作是一个空间低通滤波器,MTF则表征了该滤波器对不同空间频率的衰减程度,如图2所示。

图2 MTF表征系统对不同频率的衰减作用Fig.2 MTF characterizes the attenuation effect of the system on different frequencies
刃边法是一种常用的MTF测量方法,如图3所示。该方法测量条件简单、能够较为完整地获得系统的MTF曲线,对噪声有一定的容忍度,其关键在于垂直于刃边方向的灰度变化情况的提取。

图3 刃边法计算过程Fig.3 Calculation process of edge method
2 装置的系统组成及工作原理
所提出装置的测试系统针对一个TDICCD相机展开设计。整个系统由目标生成装置、运动装置及平行光管组成。设备工作在可见光波段,要求相机工作积分级次为32级时,测试系统在奈奎斯特频率fN处测量精度达到±0.05。整个系统的结构如图4所示。

图4 系统组成Fig.4 System composition
在测试时,将被测系统置于光管前的合适位置,根据需要设置动态目标发生器的运动状态。运动的靶标经过准直系统后由被测系统成像,对成像结果进行分析,从而实现对相机性能的评估。整套系统处于大理石平台上,以减少外界对测试结果的影响。
多个光学子系统的整体传递函数满足相乘律原则[2],整个系统的MTF可以表示为各部分MTF的乘积:

由式(1)可见,任意一个环节均会对设备的MTF测量造成影响,而各个部分的影响都不可能从原理上进行消除,因此需要严格控制各个部分MTF对系统测试的贡献。为了达到精度要求,需要将总的测量精度分解到各个部分。
2.1 目标生成装置
照明系统同靶标一起构成目标生成装置,其作用是提供一个理想的目标。照明系统是用来对靶标进行均匀、明亮照明的装置,它的照明均匀性会直接影响系统MTF的测量。综合考虑常用的照明方式之后,本文选择了双排复眼照明系统[6],该方法是目前最有效的匀光手段,通常可以实现很高的照明均匀性[7]。
照明系统的结构如图5所示。采用Tracepro软件的10 000万条光线仿真结果如图6所示。照明均匀度公式为:

式中:Iunif为照明不均匀度;Imax、Imin分别为最大光强与最小光强。由式(2)可得,在靶标尺寸范围内,其照明均匀性能达到99%。实测其均匀性为98%左右,在奈奎斯特频率fN处造成的传递函数约为0.98。
靶标是被测光学系统成像的目标。根据所采用的测量方法不同,靶标的图案也不同。本文主要使用刃边靶进行测试。刃边靶标如图7所示,这种靶标制作简单、使用方便。为了提高测量精度,在测量时通常采用倾斜刃边法的方法[8-12]。由于靶标的加工工艺成熟,且所需的图案简单,故可忽略靶标对测量结果的影响。

图5 照明系统光学组成Fig.5 Optical composition of illumination system

图6 照明系统仿真结果Fig.6 Illumination system simulation results

图7 刃边靶标图示Fig.7 Illustration of edge target
2.2 四维运动平台
为了实现TDICCD的成像及目标生成装置与准直系统光轴的对准,本文设计了一个四维运动平台,其结构如图8所示。
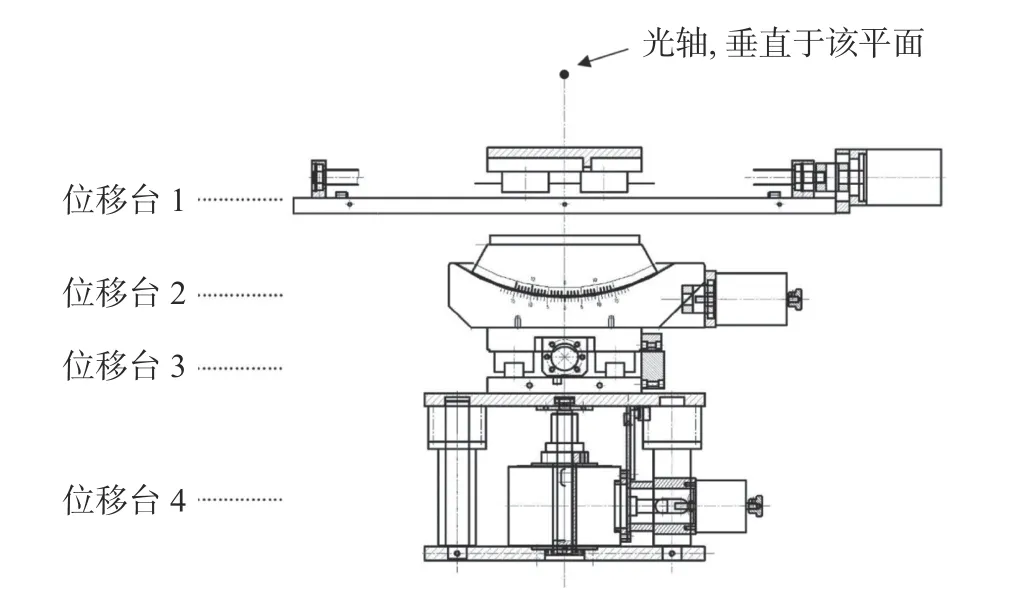
图8 四维运动平台正视图Fig.8 Front view of four-dimensional motion platform
在图8中,位移台1是一个水平位移台,靶标固定在这个平台上。位移台1可以在垂直于光轴方向的水平面内匀速运动,实现被摄目标与相机之间的相对运动。相机像面处TDICCD的扫描速度在某行频下为v2,公式为:

式中:f1、f2分别为平行光管和被测系统的焦距;v1、v2分别为平行光管焦平面处的速度与对应TDICCD的扫描速度。根据式(3),结合实际情况,可以选定位移台所需要的运行速度。
在TDI方向,速度不匹配所造成的MTF可以由下式计算[13-15]:

式中:f为空间频率;m为TDI级次;a为CCD像素尺寸;v为电荷转移速度; Δv为电荷转移速度和焦面上图像移动速度的差值。对式(4)进行理论仿真得到图9。
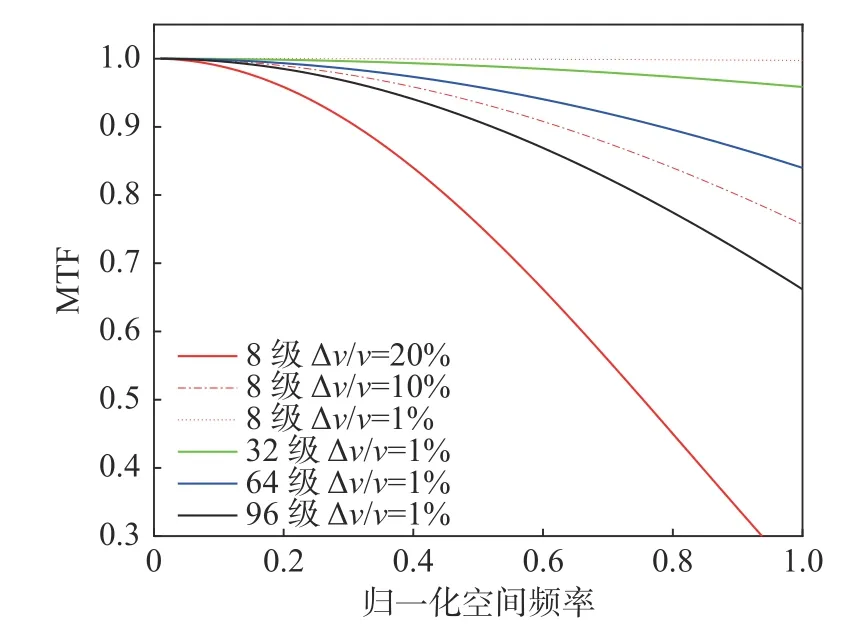
图9 不同级数、速度失配时引起的TDI方向的MTFFig.9 MTF in TDI direction caused by different stages and speed mismatch
位移台2用于实现偏流角的产生,均匀光源被固定在位移台2上。位移台2可以围绕着平行光管的光轴所在直线旋转,其作用是实现实际成像过程中偏流角的模拟。卫星在特定轨道飞行时,偏流的变化范围大概在在±3°,同时考虑到未来增加其适用范围,将转台角度的变化范围选择为±14°。
偏流角在垂直于TDI方向上造成的MTF可表示为[13,16]:

偏流角在TDI方向上造成的MTF可被表示为:

图10为根据式(5)、(6)所得的仿真结果。由图10可见,偏流角θ主要影响的是垂直TDI方向上的MTF,在TDI方向上虽然也有影响,但一般可以忽略。

图10 不同积分级次、不同偏流角对TDI方向及垂直TDI方向MTF的影响Fig.10 Effects of different integration levels and different bias angles on MTF in TDI direction and vertical TDI direction
位移台3可以沿着光轴方向运动,从而将靶标移动到平行光管的焦面位置。在实际场景中,只需要移动到允许的焦深范围ΔZ内即可,焦深范围ΔZ可被表示为:

式中u为光管的数值孔径。根据式(7)可以计算出平行光管的焦深范围ΔZ,从而选择位移台3的精度。
位移台4是一个升降台,可以实现靶标上下位置的调整,并且需要在相机装调时对靶标的条纹与TDICCD进行像素级对准,可表示为:

式中:f1、f2分别为平行光管和被测系统的焦距;d1、d2分别为平行光管焦平面处的物理尺寸与对应的被测系统像面处的物理尺寸。结合CCD像素尺寸信息,可以得到CCD投影在靶面上的尺寸,根据该尺寸可进行位移台4精度的选取。
根据以上分析、测量精度要求及现有条件,对各位移台的精度选择如表1所示。

表1 四维位移台的参数选择Tab.1 Parameter selection of 4D translation stage
2.3 光学准直系统
光学准直系统是用来产生无穷远目标的设备。为了测量的准确性,平行光管的焦距至少应为被测系统的2~5倍[17]。考虑到被测系统的焦距,本文选择了一个焦距值为7500 mm,口径为400 mm的离轴抛物平行光管,其结构如图11所示。

图11 平行光管结构Fig.11 Structure of collimator
图12为实测的平行光管在的轴上及轴外波前图像,其RMS小于 λ /14 。

图12 平行光管波前测试结果(轴上、轴外)Fig.12 Wavefront test results of collimator tube (on-axis, off-axis)
图13为平行光管实际轴上MTF与理论MTF。可以看到,该平行光管的MTF曲线已经接近衍射极限,修正后在系统奈奎斯特频率fN处对测试结果的MTF影响大概在0.98左右。

图13 平行光管实测MTF与理论MTFFig.13 Measured MTF and theoretical MTF of collimator
2.4 精度分析
对以上各部分的影响做一个总结,如表2所示。

表2 TDI级数为32时系统各部分在奈奎斯特频率fN处对结果的影响Tab.2 The influence of each part of the system over the result at the Nyquist frequency when the TDI level is 32
可见其在奈奎斯特频率fN处的影响在0.95左右,精度满足了设计要求。
3 实验结果及分析
在实验测量过程中,首先将被测相机放置在平行光管前的合适位置,调节四维调整台使得靶标处于恰当的位置。调节位移台1速度使之与TDI速度相匹配,使用被测系统进行图像采集。受限于测试条件,本次实验主要在行频为1000 Hz、积分级次为8级时进行,采集到的图像如图14所示。

图14 TDICCD采集到的速度匹配图像Fig.14 The image collected by TDICCD
对刃边图样进行MTF计算,在其奈奎斯特频率fN范围内得到的曲线如图15所示。

图15 刃边法测得TDI方向的MTFFig.15 The MTF in the TDI direction measured by the edge method
在fN/2 处附近选择一空间频率f为27.71 lp/mm,刃边法测得结果为0.121,鉴别率靶测得的结果为0.143,两者相差较小,可以认为两种方法测量结果一致。
图16是TDI级次为8级时、速度失配分别为±10%、±20%时所获得的图像。
此时由于实际的采样间隔的变化,获得的图像相对于速度匹配图像存在明显的几何畸变,在计算MTF时要加以修正。计算所得的MTF曲线如图17所示。
不同情况下8级TDI时在空间频率f为27.71 lp/mm处的MTF值以及由速度失配引起的MTF及其理论值如以表3所示, 可见其实测值与理论值相符。
图18显示了无偏流角θ时与存在偏流角θ时TDI方向上的MTF,两者保持一致,与之前的理论分析结果一致。偏流角θ对TDI方向上的像质影响不大。

图16 速度失配±10%和±20%Fig.16 Speed mismatch ±10% and ±20%

图17 速度失配对TDI方向MTF的影响Fig.17 The effect of speed mismatch on MTF in the TDI direction

表3 8级TDI时速度失配引起的MTF与理论值的对比Tab.3 Comparison of MTF theoretical value and actual value caused by velocity mismatch at 8-level TDI

图18 有无偏流角时获得的图像及TDI方向的MTFFig.18 The image obtained with or without drift angle and the MTF in the TDI direction
4 结 论
本文提出了一种对微结构TDICCD相机动态MTF地面模拟的测试装置,针对TDICCD的成像特点,设计了相应的结构,实现了对相机在轨运行时速高比v/h及偏流角θ这两个主要因素的模拟。其中照明系统采用双排复眼的结构,靶面处照明不均匀度优于2%。四维位移台各方向均根据需求选定了对应的精度。平行光管轴上波前小于 λ /14 ,接近衍射限。经过理论分析及试验验证,其测试精度满足测试装调需求。本文只对速高比v/h、偏流角θ这两个因素进行了模拟,下一步工作可以添加对震动、离焦、卫星姿态等其它因素的模拟。
