基于粒子群算法的应变传感器的优化布置

叶海林 刘路 李素贞

[摘  要]：文章针对构件损伤识别中应变传感器的优化布置问题，提出基于粒子群算法的应变传感器的优化布置方法，首先根据结构发生损伤前后应变振型的差异性，曲线拟合得到应变传感器的区域检测概率模型，求解得到传感器的最优数目;其次，基于粒子群算法分别得到在2种不同的适应度函数下的最优解。这种方法最终建立起和损伤程度一一对应的布置方案。算例分析表明：采用该方法在减少应变传感器数目的同时，也能够达到精确定位损伤杆件位置的目的。

[关键词]：损伤识别; 应变传感器; 优化布置; 曲線拟合; 识别概率; 粒子群算法

TV312A

海洋平台所处的环境十分恶劣，风、浪、流、冰和海底地震等荷载作用对平台的安全构成严重威胁。同时，由于环境腐蚀、海生物附着、构件材料老化、疲劳损伤等都将成为威胁平台结构构件和整体抗力的因素，这些作用会使得结构出现损伤，影响平台结构的服役安全性和耐久性[1]。因此需要对海洋平台结构及构件进行损伤监测，确保海洋平台的安全正常运行[2]。

总体来说，损伤识别的方法主要分为2类，第1类是常规检测技术和手段，第2类是监测技术。第1类的方法较为机械，工作量较大而效率较低，且安装实现难度大，不易于连续实时监测，因此第2类方法得以广泛的关注和研究。第2类方法即通过建立传感器网络对结构的响应信息进行监测，并对采集到的结构信息进行数据分析，进而对结构的损伤进行定量的评估。

在传感器网络中，如果传感器数目布置过少，则会大大降低识别精度;如果传感器数目过多，会造成计算量加大，数据冗余，经济上也不可取。因此如何合理地选择传感器类型以及布置传感器，从而达到经济性和有效性的统一是传感器优化问题的关键[3]。目前传感器的优化布置方法主要大致分为2种，一种是传统算法，如运动能量法[4]、QR分解法[5]、有效独立法[6]，这些算法都有各自的局限性;另一种是以神经网络、遗传算法为代表的非传统算法，具有较高的优化能力和全局能力，不易陷入局部最优。以上的大多都是对加速度传感器的布置方案进行优化，而针对应变传感器的优化布置工作却研究较少。李德春等[7]提出基于克隆选择和离散粒子群的混合算法，并将该方法应用在拉西瓦拱坝上的应变传感器的优化布置中;高长青等[8]以8 m天线臂架为研究对象，通过模态误差贡献率法（MER）法有效地解决了大型空间桁架结构中应变传感器的布置问题;莫徽忠[9]提出基于改进型遗传算法的光纤光栅传感器网布的优化布置方法，对传感器的布置角度进行了优化等等。不过以上研究仅限于在规定传感器数量的前提下研究最优布置，在确定传感器数目方面，缺少相应的研究。而在传感器布置方案中，确定传感器的最优数目也是非常重要的一环。

本文以一导管架结构海洋平台为对象，针对构件损伤识别中应变传感器的优化布置问题，提出了基于传感器的区域检测模型的最优数目确定方法，并利用粒子群算法对应变传感器的最优布置方案进行了设计。

1 基于应变模态的损伤识别方法及应变传感器优化布置技术框架

当结构构件发生损伤时，结构的应变模态会发生变化，同时也可以通过比较损伤前后应变模态的改变进行损伤定位。由此可定义结构第i阶的应变模态差值见式（1）。

Δεi，j=ψuij-ψdij（1）

式中：Δεi，j为损伤前后第i阶模态j节点的应变模态差值，ψuij、ψdij分别是损伤前、后第i阶模态j节点的应变模态。

通过应变模态差的突变从而确定损伤的位置，可以通过幅值的大小确定损伤的程度。

相对于加速度传感器，应变传感器在监测结构损伤方面有其独有的优势：灵敏度高，能感应出极其微小的应变，且应变模态对杆件局部损伤较位移模态敏感;尺寸小，重量轻，适合较大规模布置;具有较好的环境适应性，抗干扰能力强，能在各种严酷环境中工作;对测试对象的影响较小等等。因此本文主要探讨应变传感器优化布置问题。

基于应变传感器的优化布置问题，本文的总体框架主要分为2个步骤：第一，确定某损伤程度下对应的应变传感器最优数目;第二，通过寻优算法（粒子群算法）迭代求得传感器的最优布置方案。最终建立起损伤程度、传感器最优数目及最优方案一一对应的关系。以下将2个步骤分别展开介绍。

2 传感器最优数目的确定

2.1 传感器的区域检测模型

通常认为传感器的检测概率是有一定范围的。当被检测目标位于传感器的检测范围内，传感器的检测概率随传感器到被检测目标的距离增大而减小;当被检测目标位于传感器的检测范围之外，传感器检测到被检测目标的概率大大减小，几乎完全不能被检测到[9]。因此可以将这种检测概率可以大致写成式（2）。

Pij=pijd≤d0

0d≥d0（2）

式中：pij表示传感器检测到被检测目标的概率，i表示传感器的所在点号，j表示被检测目标所在传感器的所在点号，d表示传感器与被检测目标之间的距离，d0表示传感器的检测阈值距离。

2.2 利用传感器的区域检测模型确定数目

如果传感器的数目为N，并假定损伤源为检测目标，那么对于任意一个损伤源，传感器网络系统中所有传感器的检测概率表示为式（3）[9]。

Pj=1-∏Ni=1（1-Pij）（3）

设定系统中有M个损伤源，那么传感器检测到系统中所有损伤源的概率平均值表达式见式（4）。

P=∑Mj=1PjM （4）

当式（4）表示的网络系统中所有传感器对损伤源的检测概率平均值达到最大值或趋于稳定值时，得到的传感器的最小数目即可认为是布置传感器的最优数目。

3 传感器最优布置方案的确定

3.1 传感器的最优布置原理

对于一个多自由度系统，它的运动方程见式（5）、式（6）。

MX··+DX·+KX=P（5）

X=qΦs+ε（6）

式中：M、K分别为系统的质量、刚度矩阵，D为结构阻尼矩阵，P为外力作用。X为系统的位移向量，Φs为结构的位移振型，q为模态坐标，ε代表均值为0，方差为σ2的高斯白噪声的影响。

系统的位移向量X可以通传感器得到的模态向量线性无关信息得到，但模态坐标q很难得到，一般要对其估计，得到其估计值见式（7）。

Na=（X-qΦs）T（X-qΦs）（7）

当Na取最小值時，此时得到模态坐标估计值。因此将Na对模态坐标q求导，令导数为零，可以得到模态坐标的最小二乘估计值表达式为式（8）。

=（ΦsTΦs）-1ΦsX（8）

可以经数学分析得到是模态坐标q的无偏估计。此时，计算q和的协方差为式（9）。

C=1σ2ΦsTΦs-1=1σ2Q-1（9）

式中：Q为Fisher信息阵，它能够度量结构响应包含信息的多少，因此可以通过将Fisher信息阵行列式最大化来优化传感器设置[10]。

3.2 粒子群算法（PSO）

粒子群（PSO）算法最初是在1995年由Eberhart和kennedy受鸟群捕食行为的启发而提出的，他的思想可以简单表述为：每个优化问题的解空间里面的元素都可以看作为一个约束在搜索空间的粒子，每个粒子有一个速度向量来决定他们飞翔的方向和距离，而这些所有的粒子都有一个被目标优化的函数（称之为适应度函数）决定的适应度值，然后粒子们就追随在解空间中的搜索最优的位置。粒子群的主要是通过迭代首群随机粒子，通过迭代找到最优解的过程。在每一次迭代中，粒子下一时刻的速度和位置由3个方面决定[11]：

（1）粒子当前的速度，用来说明粒子目前的状态。

（2）个体的历史最优位置，使粒子有较强的自我历史搜索能力。

（3）群体最优位置，这是一种共享信息，使粒子具有较好的全局搜索能力。

其数学描述为：一个由q个粒子组成的粒子群在D维搜索空间中以一定速度飞行，每个粒子都有当前位置、历史最好位置和速度3个属性。假设当前为第t代，那么对于D维搜索空间中的第i个粒子可以表示为：

粒子位置：Xti=xti1，xti2，xti3…xtiD

粒子速度：Vti=vti1，vti2，vti3…vtiD

粒子的当前个体最优：Pti=pti1，pti2，pti3…ptiD

当前群体最优：Pg=pg1，pg2，pg3…pgD

此时计算各个粒子的适应值，因此可以确定在第t代时每个粒子的当前最优位置和当前群体最优位置，然后根据当前速度、个体最优位置和群体最

优位置3个方面来更新它的的速度和位置，即式（10）、式（11）[12]：

vt+1id=ωvtid+c1r1ptid-xtid+c2r2pgd-xtid（10）

xt+1id=xtid+vt+1id（11）

式中：vtid表示第i个粒子第t次迭代过程中第d维的速度;i=1，2…q，q为种群中粒子数目;t=1，2…Tmax，Tmax表示最大迭代次数;d=1，2…D表示搜索空间的维数;c1、c2为加速系数，其作用是调节粒子速度，使其在使得自我和社会认知能力上保持均衡，一般取正常数;r1、r2为[0，1]上均匀分布的随机数;ω称为惯性权重，其作用是用来表明当前速度对下一时刻粒子速度的影响。从表达式可以看出，惯性权重越大，粒子当前速度的影响越大，有利于跳出局部极值点;反之，惯性权重越小，粒子当前速度的影响越小，有利于算法的收敛性。线性递减惯性权重表达式（12）。

ω=ωmax-ωminTmax-NTmax+ωmin（12）

式中：ωmax、ωmin分别表示为表示惯性权重的最大值和最小值，0.1≤ωmin≤ωmax≤0.9;N、Tmax分别表示当前迭代次数和最大迭代次数。

粒子群算法的具体步骤[13]（图1）：

步骤1：初始化群体;步骤2： 计算每个粒子的适应度值;步骤3： 比较粒子适应度值与个体最优值Pi，如果优于Pi，则将当前的位置作为Pi;步骤4：比较所有粒子中个体最优值Pi与群体最优值Pg，如果Pi优于Pg，则将该粒子的个体极值Pi设置为Pg;步骤5：根据式（10）和式（11）更新粒子的速度和位置;步骤6：当迭代次数达到最大迭代次数时，停止运算，且输出Pg及对应的适应度值，否则转到步骤2。

3.3 基于粒子群算法（PSO）的应变传感器最优布置的实现流程

应变传感器最优布置流程见图2。

4 算例分析

4.1 算例概况

以一海洋观测塔（平台）作为数值分析算例。基本数据为：该观测塔水深70 m，总高度114 m，其中导管架部分13.5 m，其上的风塔100 m，生活平台高0.5 m，以及结构各部分构件几何尺寸见表1。

4.2 建立有限元模型

管架平台模型主要采用了4种单元模型：PIPE16，PIPE59，BEAM4，及SHELL181。下部导管架和上部甲板框架的主要竖向支撑构件采用PIPE59 单元，泥线以下采用PIPE16 单元，甲板平面下的支撑结构采用BEAM4 单元，水平甲板采用SHELL181 单元。风塔全部采用PIPE16 单元（图3）。

（1）PIPE16 单元由外径和壁厚确定。

（2）PIPE59 单元截面由外径、壁厚、法向曳力系数、法向惯性系数、内部液体密度、外部附着物密度、外部附着物厚度确定。

（3）BEAM4 单元截面形式选用矩形，单元参数包括截面的高度、宽度、面积和截面惯性矩。

（4）SHELL181 单元参数包括四节点处的厚度。

有限元模型采用同一种钢材，弹性模量2.1×1011 Pa，泊松比0.3，密度7 850 kg/m3 ，屈服强度360 MPa 。

4.3 模态分析

利用Ansys对该模型的前5阶模态进行分析，提取结构的频率和振型分别如表2和图4所示。

4.4 应变传感器最优数目确定

考虑到实际应变传感器可能的布置情况，关于应变传感器数目的确定及其最优布置，仅讨论应变传感器布置在泥面上主导管架杆件中部的情况。

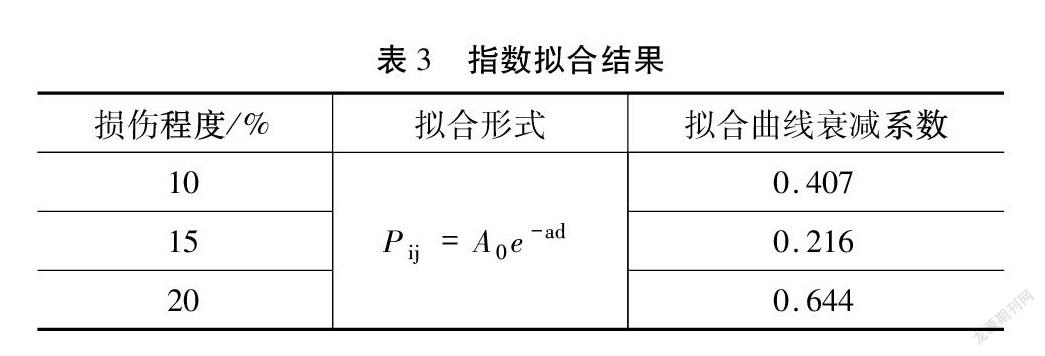
首先应计算应变传感器的区域检测概率模型。本文计划流程如下：模拟杆件的损伤，绘制损伤前后的损伤杆件应变振型差值曲线[15]，通过对该差值曲线进行拟合（指数拟合），得到传感器的应变差值随距离变化的表达式，可以近似认为该表达式为传感器检测概率模型。在不考虑系统中各传感器的差异和构件各处发生损伤的概率差异的条件下，系统中各个传感器的区域检测概率模型均一致。得到的应变差值曲线及曲线拟合的结果分别如图5和表3所示。

得到传感器的区域检测概率模型后，组建系统的检测损伤平均概率表达式，并对其最大化，得到相应传感器的数目，即认为得到该损伤程度下的应变传感器的最优数目，结果见表4。

4.5 应变传感器的最优布置方案

根据最优数目的结果，选取测点数目为5、8、10时，分别采用粒子群算法对应变传感器进行最优化布置。选取的优化准则有f1和 f2，具体的表达式见式（13）、式（14）[7]：

f1=αdet（Q）=αdet（ΨTΨ）（13）

f2=β∑mr-1∑ni-1ψ2ir∑ni-1ψ2irdet（ΨTΨ）（14）

式（13）中，Q為Fisher信息矩阵;式（14）中，α、β为调整参数，作用是将适应度值可以根据要求调节其范围。

f2引入了能量的概念，目的是使测点的模态应变能量与目标模态线性无关。基于2种适应度函数的优化配置结果如表5所示。

为了比较此2个适应度函数计算下应变传感器布置方案的性能，分别选取模态应变能和应变模态相关系数2种特征量对2个适应度函数得到的方案进行计算选优。2种特征量的表达式见式（15）、式（16）[7]：

E=∑mr-1∑ni-1ψ2ir∑ni-1ψ2ir（15）

MACij=ΨTiΨj2ΨTiΨiΨTjΨj（16）

基于以上2种特征量，测点数目为5、8、10情况下2种适应度函数的寻优性能比较见表6。

从表6可以看到，第2个适应度函数所对应的方案在模态应变能和应变模态正交系数方面均优于第1个适应度函数。因此选用第2个适应度函数下的最优布置方案，得到的最优布置方案如图6所示。

为了验证所得布置方案的有效性，分别设置不同的损伤工况，以检验是否能够通过上述布置方案较为准确地判断损伤位置。设置的损伤工况及杆件编号、应变传感器编号说明见表7和图6。

分别提取损伤前后应变传感器所测得的杆件的应变模态，并作差得到应变模态差值，可得到损伤前后的应变模态差值，如图7～9所示。从图中可以看出，损伤构件所在层的杆件应变差值均有明显突变，因此利用上述的应变传感器布置方案均可以有效对损伤构件的所在层号进行定位，传感器布置方案有效。

5 结 论

（1）针对应变传感器的优化布置问题，本文采用了2步走的流程。第一，传感器最优数目的确定;第二，确定应变传感器数目的前提下采用粒子群算法对布置方案进行优化。

（2）关于传感器数目的讨论，首先模拟了杆件的损伤，通过损伤前后的损伤杆件应变振型的差值，绘制差值曲线，通过对该差值曲线进行拟合，得到传感器的应变差值随距离变化的表达式，可以近似认为该表达式为传感器区域检测概率模型。在不考虑系统中各传感器的差异和构件各处发生损伤的概率差异的条件下，建立起系统中各个传感器检测到损伤的概率表达式对该表达式取得最大或趋于稳定时计算得到的传感器的数目即为该损伤程度下传感器的最优数目，不过该方法只能用于粗略估计所需要的应变传感器数目。

（3） 针对传感器最优布置方案问题，方法采用粒子群算法。首先针对此结构选取了2个目标函数（称之为适应度函

数），分别计算得到2种不同的优化结果，最后根据模态应变能和应变模态正交系数两个特征量比较了2种适应度函数的寻优性能优劣，最后择优选择较优适应度函数下的优化布置方案。

（4） 最后对所得的应变传感器布置方案进行验证，结果表明利用布置方案均可以对损伤杆件所在层号进行定位，传感器布置方案有效。

参考文献

[1] 钱晓东， 马汝建. 基于模态参数的海洋平台结构损伤诊断[J]. 济南大学学报（自然科学版）， 2011， 25（4）：383-386.

[2] Yang Chen J.Damage detection in offshore platflom by the random decrement technique[J].Journal of Resource Technology，ASME， 1984，106（1）：33—38.

[3] 吴子燕， 代凤娟， 宋静， 等. 损伤检测中的传感器优化布置方法研究[J]. 西北工业大学学报， 2007， 25（4） ：503-507.

[4] Worden K，Burrows A P.Optimal sensor placement for fault detection[J].Engineering Structures，2001，23（8）：885-901.

[5] Schedlinski C，Link M.An approach to optimal pick up and exciter placement[C]f//Proceedings of 14th International Modal Analysis Conference.Dearborn，USA， 1996：376-382.

[6] Kammer D C.Sensor placement for on-orbit modal identification and correlation of large space structures[J]. AIAA Journal，1991，26（1）：104-121.

[7] 李德春， 何龙军， 陈媛媛， 等. 基于改进粒子群算法的应变传感器优化布置[J]. 振动.测试与诊断， 2014， 34（4）：610-615.

[8] 高长青， 杜敬利， 张腾. 基于模态误差贡献率的应变传感器优化布置[J]. 机械工程师， 2018（4）：59-62.

[9] 莫徽忠. 基于遗传算法的光纤传感器网络优化布置研究[J]. 科技通报， 2016， 32（6）：172-176.

[10] Abdullah M M，Richardson A，Jameel H.Placement of sensors/ actuators on civil structures using genetic algorithms [J]. Earthquake Engineering and Structural Dynamics，2001，30（8）：1167 -1184.

[11] 赵建华， 张陵， 孙清. 利用粒子群算法的传感器优化布置及结构损伤识别研究[J]. 西安交通大学学报， 2015（1）：79-85.

[12] 朱喜华， 李颖晖， 李宁， 等. 基于改进离散粒子群算法的传感器布局优化设计[J]. 电子学报， 2013（10）：2104-2108.

[13] Chau K W.Particle swarm optimization training algorithm for ANNs in stage prediction of Shing Mun river[J]. Journal of Hydrology，2006，329（3-4）：363-367.

[14] 曲丽敏. 体育馆结构健康监测系统中传感器优化布置研究[D]. 山東：青岛理工大学建筑与土木工程系，2016.

[15] 蒋济同， 于红理. 基于应变模态差的海洋平台构件的损伤识别研究[J]. 灾害学， 2010， 25（S1）：67-70.