冰脊间遮掩作用对冰-水拖曳力影响的实验研究

王爽，卢鹏*，祖永恒，张丽敏，王庆凯，李志军

(1.大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024)

1 引言

海冰受到大气和海洋的动力作用产生漂移，其漂移速度与拖曳系数大小密切相关[1-3]。拖曳系数表征气-冰-海系统的动量交换效率。随着海冰拖曳系数参数化趋于完善，其量值从以前的经验常数发展到随着海冰形态变化的变量[4]。海冰的形态参数包括密集度、浮冰尺寸、冰脊间距和冰脊厚度等。由于冰脊厚度一般大于海冰的平均厚度，从而影响流速的分布，产生遮掩影响[5]，而冰脊间距又会影响遮掩作用的强度。因此在海冰拖曳系数参数化中，遮掩函数把冰脊间距和冰脊厚度作为自变量来定量描述相邻冰脊间下游冰脊受到的拖曳力随着这两个变量发生的衰减。遮掩函数直接决定下游冰脊所受拖曳力的大小，对海冰漂移产生不容忽视的影响。

目前，海冰拖曳系数参数化中应用的遮掩函数主要有指数函数和幂函数两类。Hanssen-Bauer 和Gjessing[6]首次将指数衰减函数应用到冰-气界面拖曳系数参数化公式中，计算风场中浮冰间的衰减影响。Lüpkes 等[7]将该指数函数应用到大气中性分层条件下的冰-气界面拖曳系数参数化方案。Tsamados 等[8]也选用该指数函数用于同样形式的冰-气和冰-水界面的拖曳系数参数化公式中，用来描述冰脊在风场和流场中的遮掩效应（简称TS2014）。此外，Tennekes 和Lumley[9]提出遮掩强度会随着流体中结构物间的距离而变化，从而得到遮掩效应的幂函数形式。Steele 等[10]首次将该幂函数应用在冰-水界面形拖曳力参数化公式中。Lu 等[4]将此衰减函数应用于冰-水界面并提出了系统的冰-水拖曳系数参数化方案（简称LU2011）。综上可见，目前使用的冰脊拖曳力的遮掩函数都是从其他相关研究中借鉴而来的，并非针对冰脊的实际情况进行研究的结果；而且，指数函数是从陆地风场防护林研究中得出并直接应用于气-冰-水拖曳系数参数化公式中。这种移植和借鉴是否可行，是否适合冰脊间流场遮蔽效应的实际情况仍值得讨论。

作为解决上述问题的第一步，本研究关注冰-水界面上冰脊间的遮蔽效应，通过在实验室物理模型试验中模拟冰下流场，测量前、后冰脊拖曳力的差异，探究冰脊间的尾流遮掩效应，初步给出以冰脊的形态参数为变量的遮掩函数公式，用于描述多冰脊间流场衰减情况，为海冰动力学模式的进一步完善提供参考。

2 多冰脊拖曳力实验研究

本次实验室物理模拟实验在大连理工大学海岸和近海工程国家重点实验室的PIV 水槽完成，该水槽长为22 m，宽为0.45 m，深为0.6 m，有效实验长度为11.5 m。本次实验水深为0.45 m，如图1a 所示。

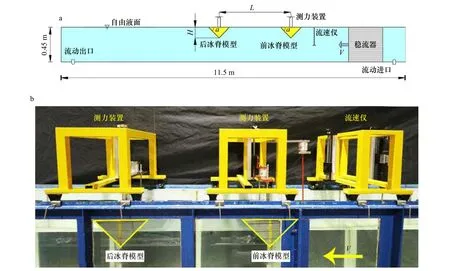
图1 实验示意图（a）和物理模型实验装置图（b）Fig.1 The sketch of the experimental study (a) and physical model test device diagram (b)

为使本次模拟冰下流场的物理模型实验接近北极海冰的真实流况，对主要参数采用动力学相似处理。首先问题的依赖参数有冰脊拖曳力F、冰脊间距L、冰脊入水深度H、水深D、流速V、冰脊底角a、流体密度ρ和流体黏性系数ν[11]。根据量纲分析原理选取H、ρ和V为独立量纲量，可以得到表1 所示的无量纲量相似依据。

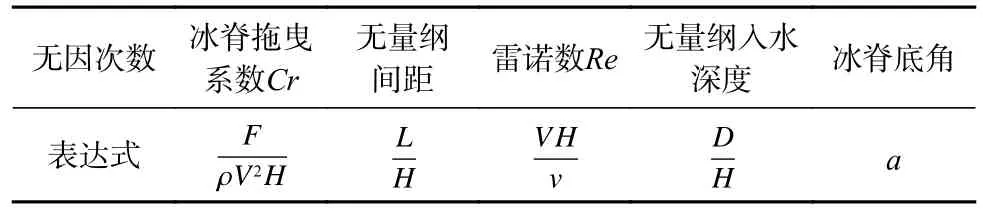
表1 模型实验相似依据Table 1 Similarity basis of model experiment

物理模型实验的设计保证无量纲参数的范围和真实海域的无量纲参数保持一致[10,12]。北极海冰的漂移速度一般不超过0.3 m/s，冰脊入水深度为2～10 m，冰脊底角范围为20°～50°[5,12]，雷诺数Re≥20 000。选用模型和原型的长度比尺λ=1/100，根据模型相似比计算得出模型的冰脊入水深度的范围是0.02～0.10 m。模型形状为底角为45°的等腰直角三角形，采用有机玻璃材料制作。与Waters 和Bruno[13]、Pite 等[14]和Zu 等[15]研究类似，该材料的表面粗糙度与真实海冰不同，但其影响仅限于表面摩阻力，对于本研究关注的形拖曳力的影响不超过0.3%，可以忽略[4]。选取的实验流速V分别为0.1 m/s、0.2 m/s、0.25 m/s、0.3 m/s、0.35 m/s。为使来流更加接近均匀流，本次实验加设稳流器，将其放置在入水口处。冰脊的入水深度H分别设定为0.02 m、0.04 m、0.08 m 和0.12 m，则物理模型实验的雷诺数Re为2 000～30 000。当Re≥10 000时，我们认为物理模型实验环境与实际海洋环境相似[11]。冰脊的间距L是本次实验研究的主要变量，由于PIV 水槽长度的限制，4 种入水深度选取了不同的间距，分别为2.5、5、7.5、10、20、30、50、70、100，共9 个间距。实验工况共145组。前后冰脊模型在竖直方向上连接量程为10 N 的拉力传感器，再固定到可移动架上，静置在水槽上方。为了排除造流机、移动架等振动对实验带来的干扰影响，本次实验加设空载，将直径为6 mm 的圆杆连接拉力传感器固定在可移动架上，如图1b 所示。为了减少不同位置流速的差异对实验准确性的影响，将流速仪和前冰脊模型的位置固定不变，通过移动后冰脊模型的位置来改变冰脊间距。由此可测量出冰脊模型在水流方向上受到的形拖曳力。

3 结果

3.1 前冰脊拖曳力

本实验研究相邻冰脊间的遮掩影响而产生的冰-水拖曳力衰减，物理模型实验结果显示，前冰脊未受遮掩效应的影响，其拖曳力值可以作为后续遮掩影响分析的基准值。图2 给出了前冰脊所受拖曳力F1随着无量纲参数间距L/H的变化。

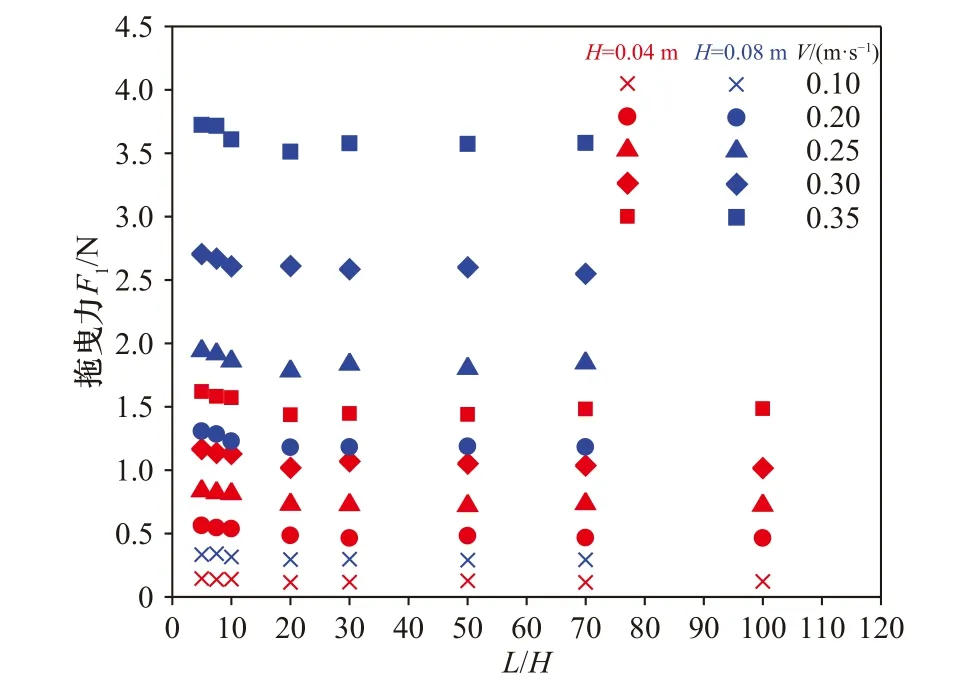
图2 前冰脊拖曳力F1 随无量纲间距L/H 的变化Fig.2 Variation of drag force of front ice ridge F1 with dimensionless distance L/H

从图2 可以看出，尽管前后冰脊间距不断变化，前冰脊拖曳力F1都表现出了良好的稳定性，其数值大小几乎与L/H无关，因此可以认为前冰脊没有受到后冰脊的影响。图2 中只呈现了H=0.04 m 和H=0.08 m两个入水深度F1的变化情况，其他入水深度组次结果的变化趋势类似。当然，流速较大时拖曳力值的浮动略大，其主要的原因是流速较大时，造流电机运行不稳定。综上，对于多冰脊实验研究，前冰脊拖曳力的变化规律与单个冰脊实验研究中的规律保持一致。目前已经有较完善的研究成果[4,16]，故本文将不再赘述。

3.2 后冰脊拖曳力

3.2.1 流速的影响

图3 给出了在不同入水深度以及冰脊间距的情况下，后冰脊拖曳力F2随流速平方的变化规律。

从图3 中可以看出，后冰脊拖曳力F2随着水流速度V的增大而增大，且F2与V2存在良好线性关系，与经典拖曳力公式吻合[17]。值得注意的是，在L/H≤7.5的小间距情况下，F2出现负值，即后冰脊产生反向拖曳力，其数值大小随着流速增大而反向增大，也保持着与V2的线性关系，与正值拖曳力形成对称现象。后冰脊拖曳力F2的大小和反转与冰下流场的形态密切相关。前冰脊尾流场的影响区域随着冰脊入水深度的增加而增大，而与流速无关[1]。在尾流后形成的漩涡场会产生相对低压区，这是产生后冰脊拖曳力的原因。随着冰脊入水深度增大，漩涡范围逐渐变大，漩涡中心也逐渐远离冰脊[3]，这使得在冰脊间距较近时，后冰脊落在前冰脊漩涡范围内从而产生反向拖曳力值；并随着冰脊间距的增加，拖曳力开始由负值到0 值再到正值。这一过程中，多冰脊遮掩的叠加对于浮冰所受到的总冰脊形拖曳力会产生较大改变，对于冰脊局地拖曳系数的确定也将产生较大的影响。

另外，图3 中冰脊拖曳力随流速平方的增长曲线的斜率实际上反映了后冰脊拖曳系数Cr的大小，拖曳系数Cr明显被分为两部分，以L/H=10 为分界。在L/H≤10 时，后冰脊受到前冰脊遮掩效果明显，此时拖曳系数Cr变化均匀，随L/H增大逐渐由负到正。在L/H≥10 时，拖曳力随速度平方的增长曲线十分集中，说明此时后冰脊的拖曳系数Cr十分接近，基本与L/H无关。为更清晰地体现这种变化，需要进一步分析F2随L/H的变化规律。

3.2.2 无量纲间距的影响

图4 给出了在不同入水深度以及流速下，后冰脊拖曳力F2随无量纲间距L/H的变化规律。从图4 的总体趋势可以看出，随着冰脊间距的增大，后冰脊的拖曳力F2不断增大直至平稳，它的变化分为3 个阶段：当L/H=2.5～10 时，尽管L/H增加较小，F2增长变化十分明显，称为迅速增加阶段；当L/H=10～30时，F2随着L/H的增长趋势相对较缓，称为缓慢增加阶段；当L/H≥30 时，随着L/H的持续增加，F2相对平稳，变化较小，称为稳定阶段。

在迅速增加阶段，拖曳力受L/H影响较大，且入水深度H越大F2增长越快，此过程中会出现反向拖曳力到正向拖曳力的变化情况。如果定义0 值拖曳力所对应的无量纲间距L/H值为临界间距值，则临界间距值主要在5～7.5 范围内；且随着入水深度的增加，临界间距值呈现出减小趋势，但是临界间距值的变化几乎与流速无关。在临界间距范围内，由于尾流漩涡场的回流作用，冰脊间流场趋近于静止，因此后冰脊拖曳力F2接近0 值。在缓慢增加阶段，小流速情况下，F2随L/H的增长已经十分缓慢；但是流速较大时，冰脊拖曳力总值较大，拖曳力受间距影响依然较大。在平缓阶段，后冰脊拖曳力F2增长缓慢趋于平稳，但是遮掩效应依然存在，后冰脊拖曳力F2逐渐接近前冰脊的拖曳力F1。当L/H超过70 时，F2的相对变化减小到不超过5%，可认为后冰脊已经离开前冰脊的尾流遮掩区[18]，不再考虑两个冰脊间的相互影响。

3.3 遮掩效应分析

由上述分析可知，后冰脊拖曳力主要受到流体速度、冰脊入水深度和冰脊间距3 个因素的影响，而前后冰脊的冰-水拖曳力比值则能直观地反映出前冰脊尾流遮掩效应的强度和范围。图5 给出了物理模型实验中前后拖曳力比值与无量纲间距L/H的关系。

图5 中的误差线表示了流速的影响，可以看到不同流速对应的拖曳力比值变化非常有限，而冰脊入水深度和冰脊间距的影响较大。将前后冰脊的拖曳力比值F2/F1与无量纲间距的变化关系进行拟合，发现两者之间有明显的指数函数关系：

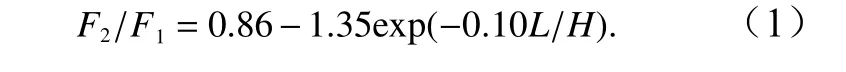
图5 中还给出了其他公式的计算结果作为比较。点划线表示的是Tsamados 等[8]在冰-气和冰-水界面拖曳系数参数化公式中所使用的指数衰减函数，即F2/F1=1-exp(-sL/H)，其中s为无量纲间距L/H的系数；虚线所表示的是Lu 等[4]在冰-水拖曳系数参数化公式中所使用的幂衰减函数，即F2/F1=[1-(H/L)1/2]2。当L/H≤20 时，指数衰减函数TS2014 表示的遮掩作用影响较弱；在L/H＞20 时，指数衰减函数TS2014 已经接近1，则遮掩效应带来的衰减不再存在。且指数衰减函数TS2014 公式来自陆地防护林实验，然而陆地防护林与海冰的真实情况存在较大差异，高密度的防护林也会允许风场通过[6]，因此指数衰减函数TS2014的不准确性主要体现在表示的遮掩影响较弱和遮掩影响的范围较小。且指数函数中s的选取没有统一确定，Hanssen-Bauer 和Gjessing[6]、Tsamados 等[8]选取s=0.18；而Lüpkes 等[7]在使用时选取了s=0.5。幂衰减函数LU2011 表示的遮掩影响相对较大一些，但是仍然可以发现与实验结果有较大出入。在L/H≤20 时，LU2011遮掩影响相对偏小，而在L/H≥20 时，遮掩影响又相对偏大。虽然整体遮掩影响的作用范围相对指数衰减函数TS2014 较大，但遮掩范围过大，在L/H=500 时仅趋近于0.91。

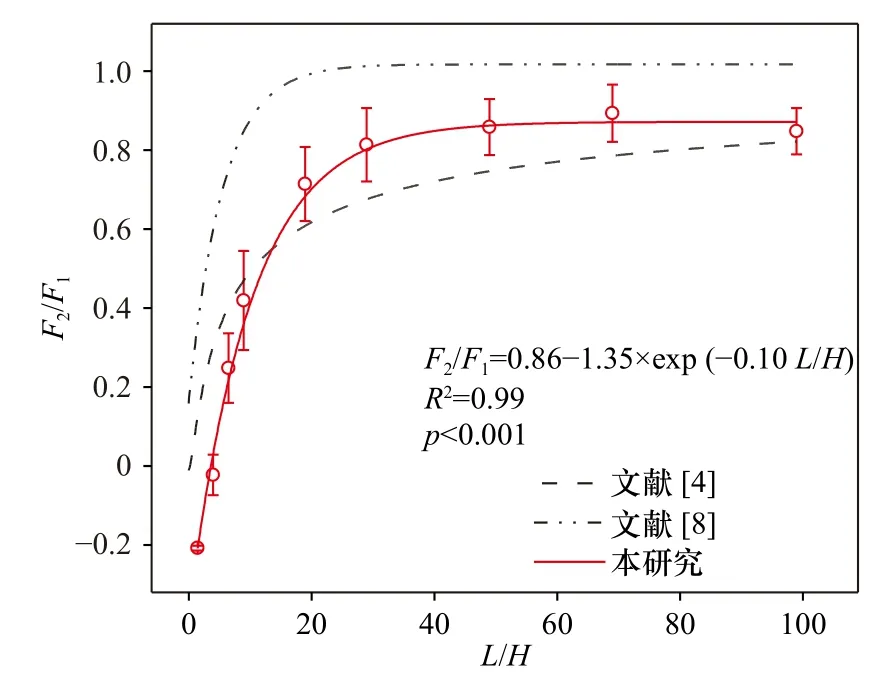
图5 拖曳力比值F2/F1 随无量纲间距L/H 的变化Fig.5 The drag force ratio F2/F1 changes with the dimensionless distance L/H

相比前两种衰减函数，本文结果显示的衰减函数可以更好地描述多冰脊之间的遮掩效应。尤其在小间距情况下，遮掩效应最为明显，且在L/H≤5 时出现反向拖曳力，即F2/F1＜0，而TS2014 和LU2011 的衰减函数均不能描述出这一特征，因为它们没有考虑到由于旋涡回流而产生的反向拖曳力会对冰脊总拖曳力产生的影响。而在密集度较高且浮冰较小的情况下，尾流的遮掩作用最强[10]，所以小间距条件在实际的海冰情况中显得尤为重要。且整体来看，式（1）所表示的遮掩影响更加符合实际情况。根据后冰脊拖曳力随无量纲间距变化（图4）可知，当L/H＞70 时，可以认为后冰脊已经离开尾流区，因此遮掩式（1）的适用范围为L/H=0～70。需要注意的是，随着间距的增大，式（1）的拖曳力比值F2/F1在超出尾流区后稳定在0.86，并未达到理想值1，与LU2011 幂衰减函数类似。这是由于在进行实验室物理模型实验时，冰脊的入水深度与实验水深在同量级，流场的演变会受到水深的明显影响；而且实验水槽水头会因水流的影响而产生损失从而导致流速衰减，影响拖曳力值的测量值[19]。该问题可以通过开展大水深条件下的物理模拟或者数值模拟研究来解决，最终得到无关水深条件的遮掩规律。

4 结论

本文以探究冰-水界面的多冰脊遮掩效应为研究目标，开展了测量前冰脊遮掩对后冰脊拖曳力影响的物理模型实验，得到了前后冰脊冰-水拖曳力在尾流遮掩情况下的变化规律，并总结出以下结论。

前冰脊拖曳力不受遮掩效应的影响，其拖曳力与流速和冰脊入水深度等变量的关系与单冰脊情况相同。后冰脊受到遮掩影响，拖曳力与水流速度的平方呈线性关系。当L/H≤7.5 时，后冰脊处在前冰脊尾流漩涡场中，从而出现反向拖曳力。后冰脊拖曳力由负值到0 值再到正值的过程中，拖曳力与流速平方的线性关系保持不变，而拖曳系数Cr呈现出先减小后增大至不变的趋势。后冰脊拖曳力F2随着L/H的增大而增大，0 值拖曳力对应的临界间距值主要集中在5～7.5 范围内，且随着入水深度的增加呈现减小趋势。在平缓阶段L/H＞70 时，可认为不再需要考虑尾流的衰减影响。

多冰脊间的遮掩效应主要受到冰脊入水深度和冰脊间距的影响，与流速无关。本实验发现，前后冰脊的拖曳力比值与无量纲间距L/H之间有明显的指数函数关系，并得到了可以更加准确描述冰下流场由于冰脊尾流所产生的遮掩影响的衰减函数，该函数直接从冰脊拖曳的物理模型实验中得到，将冰脊形态和冰脊间距对流速衰减函数的影响进行参数化表示，与现应用在海冰模式中的两种衰减函数相比，更适用于描述冰脊密集区域冰-水界面上的流速衰减过程。

作为冰脊间遮蔽作用研究的第一步，本文给出了倾角为45°的冰脊在有限水深下的实验结果，其意义在于给出初步规律以及验证研究方法的可行性。目前式（1）还不能直接应用于模式计算，下一步将通过更多的物理模型实验与数值模拟的计算，得到不同类型冰脊在无限水深情况下的结果，为海冰拖曳系数参数化的完善提供支持。