基于GAM 和GWR 模型分析环境因子对鱼类分布的影响-以山东近海多鳞鱚为例

简盈 ，张云雷 ，宋业晖 ，张崇良，纪毓鹏，任一平*

(1.中国海洋大学 水产学院，山东 青岛 266003；2.青岛海洋科学与技术试点国家实验室 海洋渔业科学与食物产出过程功能实验室，山东 青岛 266237；3.海州湾渔业生态系统教育部野外科学观测研究站，山东 青岛 266003)

1 引言

多鳞鱚（Sillago sihama），隶属于鲈形目（Perciformes）、鱚科（Sillaginidae）、鱚属（Sillago），为体长约20 cm 的小型海洋鱼类，多分布在河口和近岸水域[1]。多鳞鱚属于沿海暖水性底层鱼类，多栖息于沙泥和沙砾的海域，其肉质鲜美、商业价值高[2]。多鳞鱚是底栖生物食性鱼类，主要摄食多毛类和端足类，在生态系统物质循环和能量流动中有重要意义[3]。目前对多鳞鱚的研究主要集中在基因、摄食、生长和死亡参数估算、早期发育形态等方面[1,3-5]。有关多鳞鱚栖息地的研究罕见报道。栖息地为鱼类的生长提供适宜的生物及非生物环境，直接或间接影响鱼类的行为、丰度、渗透压调节、新陈代谢等[6-7]。此外，栖息地的丧失还可能导致生态系统的失调。

广义可加模型（Generalized Additive Model,GAM）通常用于研究物种分布和环境因素之间的关系，如李迎冬等[8]使用GAM 探究不同季节山东半岛南部海域小黄鱼（Larimichthys polyactis）分布与环境因子的关系；朱文斌等[9]基于GAM 分析了浙江沿岸日本鳀（Engraulis japonicus）幼鱼资源量受环境因子影响发生的变动。GAM 在分析数据之前，通常假定环境变量对物种分布的影响是恒定的，即假设变量间具有空间平稳性或者同质性[10]。然而，在一个大的空间尺度上，空间平稳性并不总是存在，特别是在海洋生态系统，水生生物的高度流动性和生物与环境变量之间的空间变化关系，使空间非平稳性比空间平稳性可能性更高[11]。

地理加权回归（Geographically Weighted Regression,GWR）模型本质上是改进的全局回归模型，是空间数据分析方法之一。根据采样点的坐标，GWR 模型在每个空间位置拟合出一个局部回归方程，从而得出各解释变量与响应变量关系的局部回归系数[12]。与GAM 相比，GWR 模型更适合用于研究物种分布与环境因子间的空间异质性，而不是在整个研究区域内只得到一个全局平均回归参数。GWR 模型被广泛应用于陆地上相关的研究，如杨逍遥等[13]使用GWR模型研究西安市共享单车分布情况与各影响因素的关系；丁亚鹏等[14]基于GWR 模型分析了伊河流域土壤有机碳空间分布与影响因素间的关系，并探讨影响因素的空间异质性；而其在海洋生物上的研究较少。Windle 等[15]最早应用GWR 模型探讨了海洋物种大西洋鳕鱼（Atlantic cod）分布与环境因子和生物因子的关系，并讨论了GWR 模型在渔业生态学研究上的优势。

本研究利用2016 年秋季在山东近海开展的渔业资源底拖网调查数据，使用GAM 和GWR 模型探讨环境因子对多鳞鱚分布的影响，旨在了解多鳞鱚数量空间分布特征，比较GAM 与GWR 模型的分析效果，以期为开展渔业生物空间分布研究提供新思路、新方法，为多鳞鱚资源的科学养护和管理提供基础。

2 材料与方法

2.1 数据来源

多鳞鱚样品来自2016 年秋季（10 月）在山东近海进行的渔业资源底拖网调查，调查海域为35°～38.5°N，118°～124°E。将调查海域分为莱州湾海域（A 区）、烟威渔场及其邻近海域（B 区）、山东近海南部及其邻近海域（C 区），3 个海域同时开展调查（图1）。采用定点设站的方法来进行渔业资源调查，A 区设置48 个站位，B 区设置51 个站位，C 区设置63 个站位。调查船为220 kW 单拖渔船，拖速为3.0 kn，每站拖曳时间约为1 h，拖网调查均安排在白天进行。拖网网具网口高度约为7.53 m，宽约为15 m，囊网网目大小为17 mm。同时，采用RBR-XR-420 型CTD 采集每个站位的水深（Depth）、底层海水温度（Sea Bottom Temperature，SBT）、底层海水盐度（Sea Bottom Salinity，SBS）。本次调查均按《海洋调查规范 第6 部分：海洋生物调查》（GB/T 12763.6-2007）[16]进行样品鉴定，获取多鳞鱚的密度和生物量等数据。依据拖网时间1.0 h和拖速3.0 kn 进行调查数据标准化处理，获得各调查站位多鳞鱚相对资源量（单位：g/h）[17]。

图1 山东近海渔业资源底拖网调查区域Fig.1 Bottom trawl survey areas for fishery resources in the Shandong coastal waters

2.2 分析方法

为了避免环境变量之间的共线性，通过方差膨胀因子（Variance Inflation Factor,VIF）函数检验环境变量之间的关系，筛选出适合加入模型的因子。一般认为，当VIF＞4 时，变量存在共线性[18]，因此，在建模前去除导致共线性的解释变量。

本研究应用GAM 对多鳞鱚相对资源量和环境因子进行分析[19]。GAM 利用非参数的方法灵活处理数据间的复杂联系，通过样条平滑函数反映响应变量与解释变量之间的关系。GAM 的一般表达式[20]为

式中，Y是多鳞鱚相对资源量（单位：g/h）；g（Y）为联系函数，本文采用自然对数；xj为解释变量，即各站位的环境因子；α为函数截距；fi（xj）为平滑函数；ε表示随机误差。

GWR 模型既能描述响应变量与解释变量之间的关系，又能反映空间异质性。它将数据的地理位置嵌入到回归参数中，通过每个空间位置分配的权重不同，从而在每个观测点都进行局部回归。GWR 模型的一般表达式[21]为

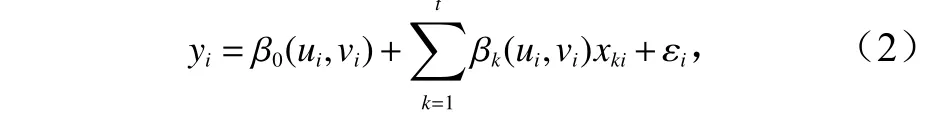
式中，ui是第i个采样点的纬度数据；vi是第i个采样点的经度数据，即（ui,vi）是第i个采样点的经纬度坐标；β0(ui,vi)是第i个采样点回归常数；βk是第i个采样点的第k个待估回归参数；xki为第i个点上第k个变量的观测值；t为解释变量的个数；εi是第i个采样点的随机误差。

GWR 模型的空间权重函数决定着局部回归系数等参数值，本文采用Gauss 函数法来确定权重函数和带宽，其公式[22]为

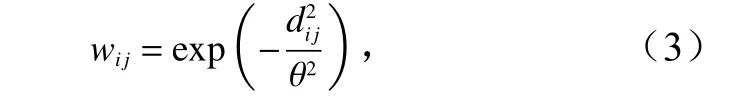
式中，i为预测点；j为观测点；wij为观测点j在预测点i的权重；dij为i、j两点间的距离；θ为带宽，是描述权重与距离之间函数关系的非负数衰减参数。带宽的大小影响着GWR 模型的分析结果，如局部回归系数值等。本研究基于赤池信息准则（Akaike Information Criterion，AIC）的自动黄金分割搜索方法选取最优带宽，即带宽最好的模型AIC 值最低。

在模型拟合过程中，依照AIC[23]、决定系数（R2）[15]和偏差解释率（Deviance Explained,DE）[15]评价模型效果，根据逐步回归的方法依次将因子加入模型中。AIC 值越低，R2和DE 越高，表明模型的拟合效果越好。

AIC 公式为

式中，D为偏差（残差平方和）；φ为离差参数（方差）；df为有效自由度。

以上模型构建过程均在R4.0.3 软件中实现，其中GAM 由mgcv 包构建，GWR 模型由spgwr 包构建，各回归系数空间变化的显著性检验使用GWmodel 包实现。

3 结果

3.1 模型构建

根据VIF 检验，水深、底层海水盐度和底层海水温度的VIF 值分别为1.57、2.17、1.51，均小于4，故本研究选取水深、底层海水盐度和底层海水温度3 个环境变量参与构建模型。

根据AIC、DE 和R2，采用逐步回归分析，最终选择水深（Depth）、底层海水盐度（SBS）和底层海水温度（SBT）作为解释变量，多鳞鱚相对资源量作为响应变量共同构建最优GAM。表达式为

式中，s()为自然样条平滑函数。其迭代过程如表1所示，最优GAM 的AIC 值为168.113，偏差解释率为31.87%，R2值为0.285。

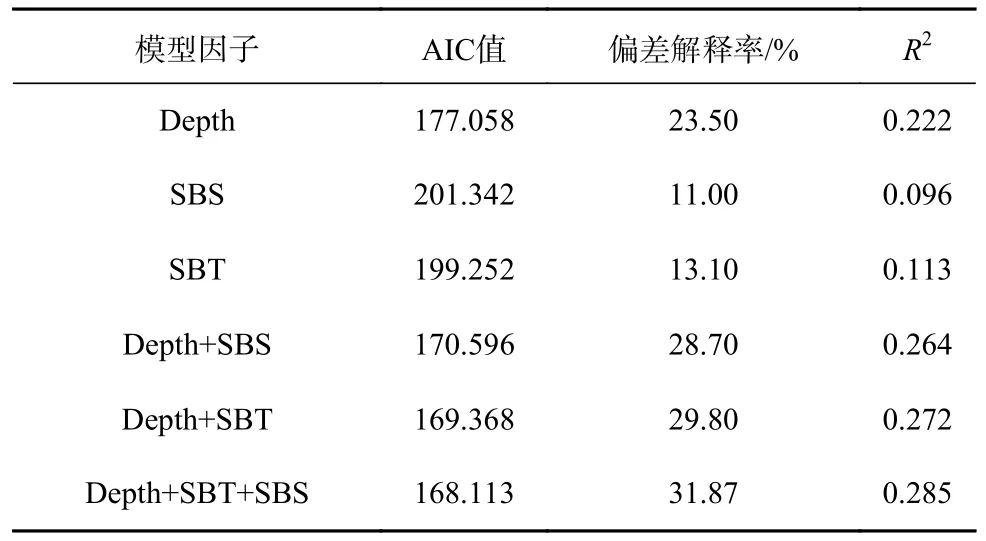
表1 GAM 变量筛选及影响因子的参数分析Table 1 The variable screening process for GAM and parameters analysis

GWR 模型筛选过程如表2 所示。通过比较各个GWR 模型的AIC 值和决定系数，Depth+SBT 模型的AIC 值最小，为126.296，R2值最大，为0.449，最优带宽为0.113。最优GWR 模型的表达式为

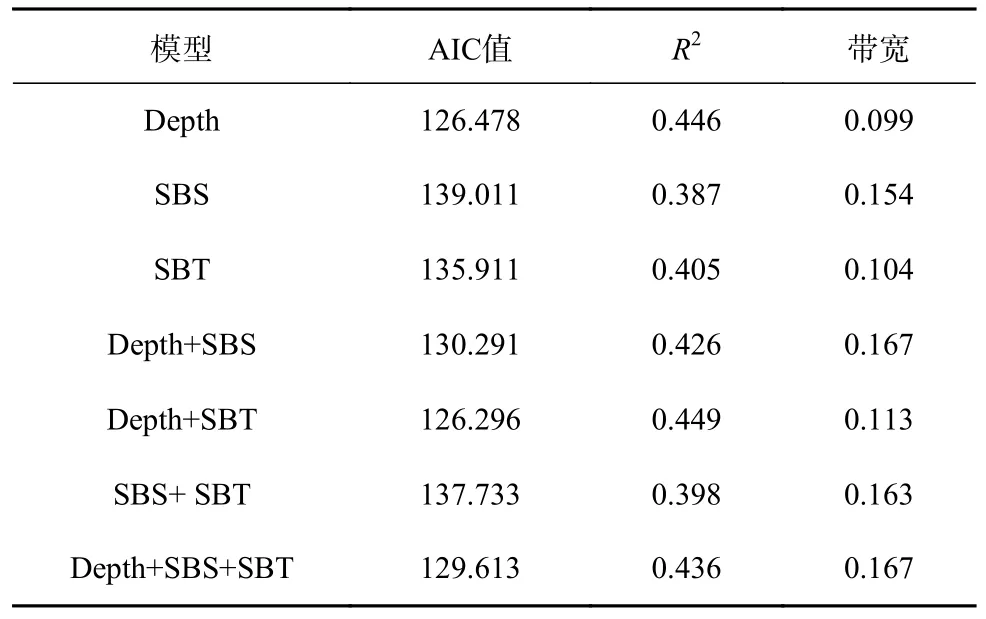
表2 多鳞鱚空间分布的环境影响因子的GWR 模型筛选过程Table 2 Forward-selection procedure of GWR model for environmental influencing factors on spatial distribution of Sillago sihama

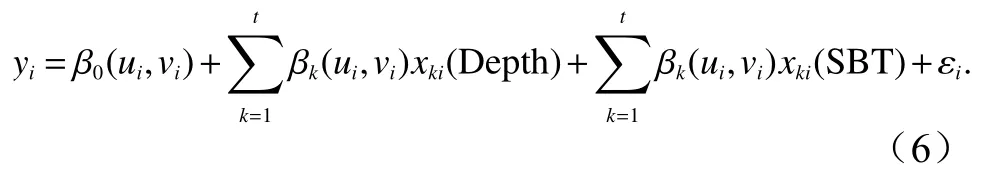
3.2 多鳞鱚空间分布

山东近海A 区、B 区、C 区共调查了162 个站位，其中A 区、B 区、C 区分别捕获到多鳞鱚的站位有41 个、10 个、11 个。多鳞鱚主要分布在山东近岸海域，在122.5°E 以东的远岸海域未捕获到多鳞鱚。大部分站位的多鳞鱚相对资源量在0～50 g/h，在150～215 g/h 的站位有2 个，分布在A 区，即37.5°～38.5°N，119°～120.5°E 的海域范围内（图2）。

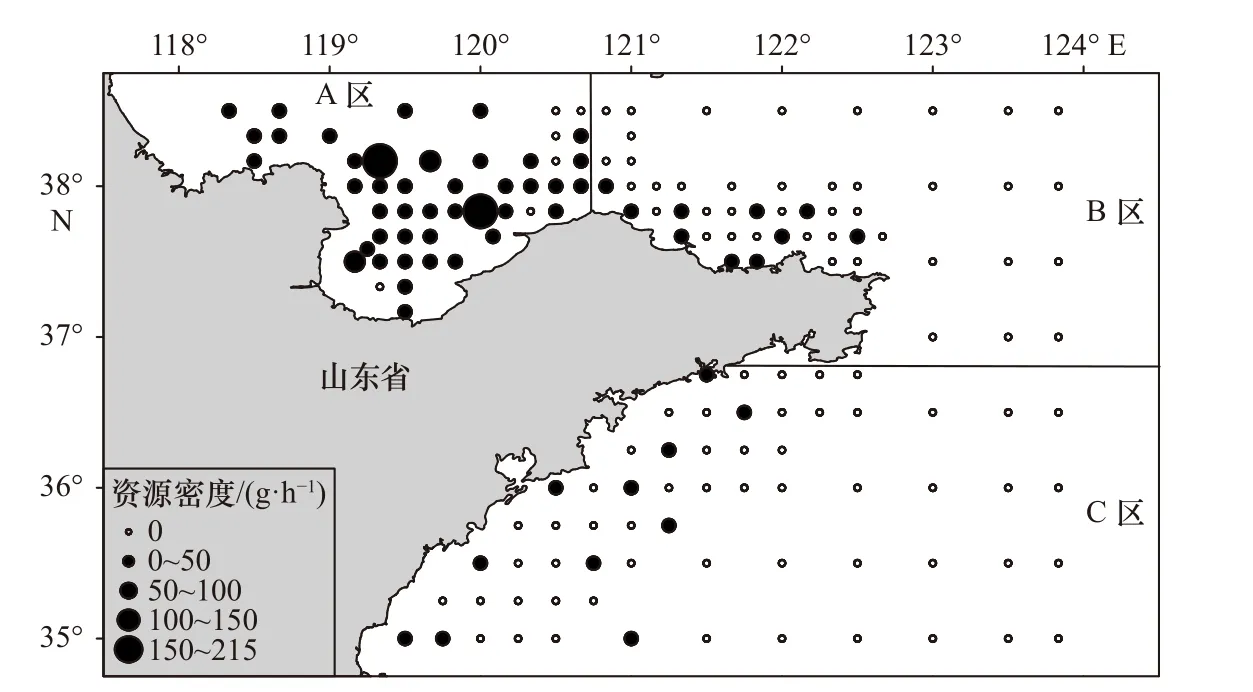
图2 山东近海多鳞鱚的空间分布Fig.2 Spatial distribution of Sillago sihama in the Shandong coastal waters

3.3 GAM 和GWR 模型对比

利用AIC 和R2指标对模型表现性能进行评估。结果显示，由相同解释变量构建的GWR 模型与GAM在不同解释变量组合中模型性能表现不同（表1，表2）。此外，分别对比具有相同解释变量组合的GWR模型和GAM 的AIC 和R2指标发现，GWR 模型具有较低的AIC 值和较高的R2值。可见，GWR 模型比GAM具有更优的拟合效果。

GAM 结果显示，在底层海水盐度、水深和底层海水温度3 个环境因子中，水深对多鳞鱚相对资源量的影响最大，其偏差解释率达到23.50%（表1）。多鳞鱚相对资源量随着深度的增加而降低（图3）。底层海水温度对多鳞鱚相对资源量的影响小于水深的影响，随着底层海水温度的升高，多鳞鱚相对资源量整体呈现先增加后降低的趋势，在19.8℃左右相对资源量达到顶峰。而底层海水盐度的偏差解释率最低，为11.00%（表1）。随着底层海水盐度的升高，多鳞鱚相对资源量逐渐升高（图3）。

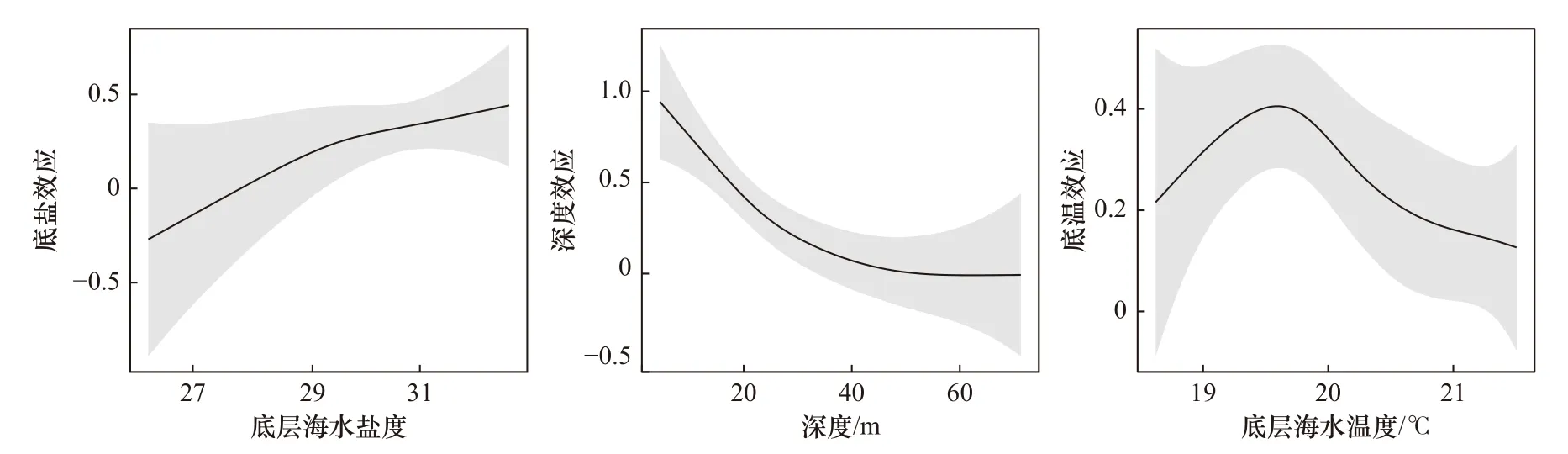
图3 GAM 中不同环境因子对山东近海多鳞鱚相对资源量的影响Fig.3 Effects of different environmental variables on relative abundance of Sillago sihama in the Shandong coastal waters in GAM

GWR 模型分析结果显示，多鳞鱚的相对资源量与水深、底层海水温度这两个环境因子之间的关系在空间上是非平稳的。从各参数上看，底层海水温度和水深对多鳞鱚相对资源量在空间上变化影响显著（p＜0.01）。截距局部回归系数的变化范围为-13.722～7.805，67.2%为负影响，32.8%为正影响。底层海水温度局部回归系数的范围为-0.349～0.755，对多鳞鱚相对资源量主要是正影响，正相关占68.8%，负相关占31.2%。水深局部回归系数的范围是-0.028～0.029，负相关占76.6%，正相关占23.4%，对多鳞鱚相对资源量的负影响多于正影响（表3）。

表3 最优GWR 模型局部参数估计汇总统计Table 3 Summary statistics of the local parameter estimates for the optimal GWR model

根据GWR 模型R2可以看出最优GWR 模型在近岸水域的表现更佳，近岸水域水深和底层海水温度的决定系数值达到0.30～0.40，远岸决定系数值大部分为0.10～0.20，少部分为0～0.10（图4）。总体上，近岸海域的模型拟合度较高，远岸模型拟合度较低。

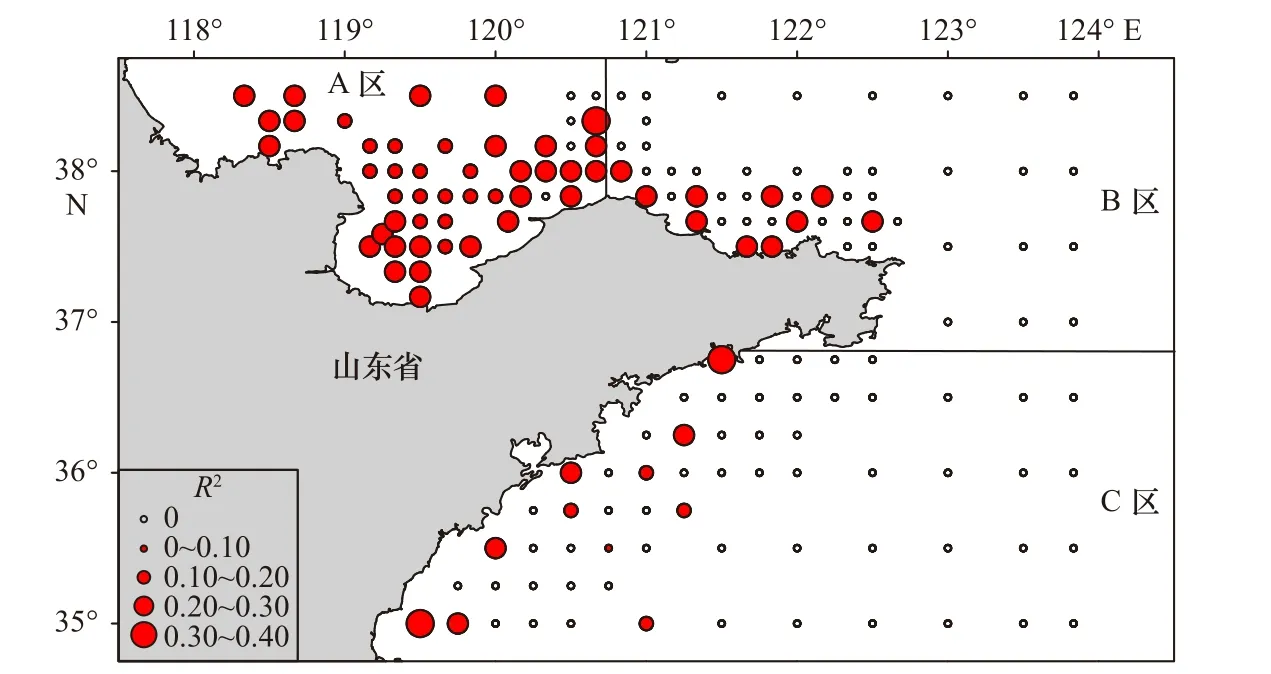
图4 最优GWR 模型决定系数（R2）的空间分布Fig.4 Spatial distribution of R2 values in the optimal GWR model

为了进一步分析GWR 模型中水深和底层海水温度对多鳞鱚空间分布的影响，分别绘制了水深和底层海水温度的局部回归系数空间分布（图5）。由图可以看出，局部回归系数随空间位置改变而改变，同一因子对不同地点多鳞鱚相对资源量的影响程度不同。在调查区域中，水深主要与多鳞鱚相对资源量形成负相关关系，底层海水温度主要与多鳞鱚相对资源量呈正相关关系。对比水深和底层海水温度的局部回归系数看出，水深和底层海水温度局部回归系数高值区均在A 区，并且底层海水温度局部影响程度高于水深，最高可达0.90，而水深局部回归系数最高仅为0.04。

图5 GWR 模型中水深（a）、底层海水温度（b）局部回归系数值的空间分布Fig.5 Spatial distribution of regression coefficient values for depth (a) and sea bottom temperature (b) in the GWR model

4 讨论

4.1 多鳞鱚的空间分布

本研究中发现多鳞鱚聚集区域虽然存在空间上的变化，但集中分布于近岸海域，这与以往的研究相一致[24-25]。值得注意的是，多鳞鱚主要分布在35°～38.5°N，122.5°E 以西的近岸海域，这可能与多鳞鱚的栖息习性有关。有调查研究发现，山东海域近岸底质类型主要为砂泥和砂砾，该特点与多鳞鱚喜栖息底质类型相一致[2,26-27]。此外，山东近岸海域具备水深较浅、营养盐丰富和饵料充足等优势，可以为多鳞鱚的生长提供有利的条件[26,28]。夏季是多鳞鱚繁殖期，产卵后开始分散索饵，之后随着温度降低逐渐向南洄游且迁移至较深水域[25,29]。可见，多鳞鱚的洄游习性对其相对资源量分布的时空变化也有影响。

多鳞鱚相对资源量较大的站位多分布在37.5°～38.5°N，119°～120.5°E 范围内，其原因可能是莱州湾海岸线较长且黄河、小清河等10 余条入海河流带来了丰富的营养盐，提高了该海域的初级生产力[30]。此外，多鳞鱚喜食底栖生物，主要摄食多毛类[24]。结合史书杰[26]对渤海底栖生物丰度和分布的研究，本研究发现多鳞鱚相对资源量高值区与底栖生物（其中多毛类丰度最大）资源分布的高值区重叠。可见，莱州湾可以为多鳞鱚提供较佳的摄食环境。

4.2 环境因子对多鳞鱚空间分布的影响

GAM 和GWR 模型结果显示，山东近海多鳞鱚分布主要受到水深、底层海水温度这两个环境因子的影响。底层海水盐度与多鳞鱚资源分布的相关性较低，这可能与多鳞鱚属于广盐性鱼类有关。沿岸、红树林、河口、沙洲等盐度变化较大海区均有多鳞鱚分布，其原因可能是在高低盐度变化交界的海域，其适宜盐度梯度有利于刺激多鳞鱚成鱼的性腺成熟[31-32]。

GAM 结果显示，水深与山东近海多鳞鱚资源分布的相关性最高，且随着水深的增加，多鳞鱚相对资源量呈现降低的趋势。多鳞鱚群体主要分布在0～60 m海域[4,33]。黄海水深10～30 m 处水温变化较大且其初级生产力高值区主要集中于中上层水域[8,34]。可见，水深差异会直接影响温度、海洋初级生产力等其他因素直接或间接对鱼类的空间分布造成影响。GWR模型结果也显示，多鳞鱚相对资源量与水深呈显著负相关关系。莱州湾（A 区）大部分水深在10 m 以内，最大水深为18 m，而黄海海域中部（B 区、C 区）水深在30～70 m 上下，由西向东逐渐加深[35]。总之，莱州湾水深小于黄海中部，更有利于多鳞鱚栖息。

底层海水温度与秋季山东近海多鳞鱚资源分布的相关性也较高。GWR 模型结果显示，莱州湾多鳞鱚分布与底层海水温度主要呈现正相关关系，而在黄海中部（B 区、C 区）主要呈现负相关关系，这表明多鳞鱚分布与底层海水温度存在空间非平稳性关系。GAM 根据所有调查数据得出的结论在某些区域不适用的原因可能是由于区域间的底层海水温度差别较大，也有可能在某些区域底层海水温度不是影响多鳞鱚分布的主要影响因子[12]。多鳞鱚属于暖水性底层鱼类，秋季B 区和C 区北部受到黄海冷水团的影响，使其周围海域温度降低，致使多鳞鱚呈零星分布[28,36]。

4.3 模型分析

本研究比较分析了GAM 和GWR 模型在拟合多鳞鱚相对资源量与环境因子关系方面的效果。研究表明，GAM 的表现劣于GWR 模型。值得注意的是，两个模型的最优模型的解释变量组成并不一致，如最优GWR 模型中缺少底层海水盐度这一解释变量。可见，模型的解释变量组合对GAM 和GWR 模型的拟合效果很重要。GAM 使用平滑函数来拟合非线性关系时，容易过度拟合[27]，而GWR 模型是基于线性相关的，过度拟合风险较小。此外，GAM 通常用于分析响应变量与解释变量间的非线性关系，得出全局统一规律，在处理复杂数据方面具有灵活方便的特点[12]。正如本研究中GAM 的结果可以直观地分析出适宜水深和温度范围。但在某些情况下，变量之间的关系不是通用的，而是取决于位置[37]。故GAM 在处理类似水深等可能存在空间非平稳性的变量时，不能全面准确反映自身的变异规律和可能的响应机制。

对比本研究中GAM 和GWR 模型结果，可以看出GWR 模型更有利于反映出空间上变量间复杂的关系，考虑空间关系的局部特征[38]。它能够根据不同的带宽在不同的观测点纳入不同的近邻点进行数据分析得出各解释变量与响应变量关系的局部回归系数，侧重于阐释空间异质性及其规律性特征，这是传统分析方法难以实现的[39]。同时，GWR 模型除考虑响应变量与各解释变量在局部范围内的特定关系外，还能考虑到该关系在全局尺度上的变化，有利于增强参数估计值对空间变化的灵敏性[22]。可见，GWR 模型在处理空间非平稳性数据时具有巨大的优越性。此外，生态数据并不都符合正态分布和线性关系的假设，GWR 模型代表使用相对较新的工具来研究空间非平稳性，在渔业数据空间动态分析中表现出了发展潜力[15]。

综上所述，本研究比较了GAM 和GWR 模型对山东近海多鳞鱚资源分布的拟合效果，当物种分布与环境变量存在空间非平稳性时，建议使用GWR 模型对物种分布进行研究，但在实际应用中，还应根据数据可获得性和实验目的不同选择合适的模型。此外，本研究中多鳞鱚主要分布于莱州湾，其相对资源量与水深、底层海水温度呈非线性关系和存在空间异质性。进一步的研究，还可以从食物网角度分析不同物种间相互作用对多鳞鱚分布的影响，进而根据山东近海多鳞鱚的分布特征和生物学特征规划保护区，这对多鳞鱚的资源管理、保护以及可持续利用具有重要意义。