动静组合加载数值模拟砂岩损伤演化规律
2022-07-09王晓雨李骞王伟张明涛王奇智
王晓雨, 李骞, 王伟, 张明涛, 王奇智
(1.石家庄铁道大学国防交通研究所, 石家庄 050043; 2.武汉地铁集团有限公司, 武汉 430070;3.石家庄铁道大学土木工程学院, 石家庄 050043; 4.河北科技大学建筑工程学院, 石家庄 050043)
在自然界中,岩石类材料随地质演变活动形成了大量的、复杂的和随机性的缺陷,这些缺陷使得岩石在动荷载作用下破坏机理和损伤规律更复杂[1]。在深部砂岩铀资源地浸开采渗透性低这一难题背景下,根据动损伤模型研究砂岩的损伤演化规律,对中国深部资源有效开采具有指导性意义[2]。
为了研究岩石的损伤破坏特征,许多学者在理论方法的基础之上进行了大量的数值模拟和室内试验,建立了岩石动态宏观和细观损伤模型。Grady等[3]从岩石内部微裂纹特征出发,分析出被激活的裂纹密度服从两参数的Weibull分布,由此建立了拉伸应变率效应各向同性的动态损伤模型。朱晶晶等[4]对花岗岩进行了霍普金森压杆(split Hopkinson pressure bar,SHPB)循环冲击试验,结合统计损伤理论和微元体强度规律,建立基于Weibull分布的动态损伤模型。高文学等[5]通过研究岩石损伤耗散能,计算能量耗散密度为建立新的动损伤模型提供条件。
在动态损伤试验和数值模拟方面,崔晨光[6]利用LS-DYNA 非线性动力分析软件建立数值试验模型,模拟岩石在不同应变率下的动态破坏过程。姚欢迎等[7]在单轴压缩条件下进行了声发射试验,并在岩石声发射特征基础上对页岩单轴压缩损伤演化规律进行了分析,提出受载岩石损伤先减小后增大结论,进一步扩展对受载岩石内部损伤演化机理的认识。张雨霏等[8]研究了含粗糙节理面水泥砂浆试块的动态破坏特征,分析了冲击荷载和试样表面形貌对节理面的影响,并通过能量法表征损伤变量。Wang等[9]以SHPB试验为基础并结合颗粒流离散元PFC2D程序,进行循环荷载作用下砂岩细观动态损伤和破坏过程分析,揭示了岩石宏观破坏机理。
汪鑫等[10]在冻融循环试验基础上,结合不同冻融次数下试样物理性质及细观结构的变化情况,采用ANSYS有限元软件进行试样冻融循环过程中应力应变及岩石内部温度变化的特征模拟,进一步揭示了英安岩冻融损伤劣化的力学机理。闻磊等[11]利用霍普金森杆对砂岩进行预加静载循环冲击,选用Logistic函数的逆函数表征岩石循环冲击损伤,进一步分析砂岩动态损伤演化特征,对其破碎形式和加载强度进行了研究。刘兵兵等[12]运用非线性显式动力分析程序ANSYS/LS-DYNA对水下钻孔爆破进行数值模拟,从不同起爆方式和不同堵塞材料方面进行分析,研究了水下钻孔爆破的效果。
大多学者在理论分析和实验研究及数值仿真方面做了大量的工作,采用不同方法建立了损伤模型,对岩石宏细观破坏机理进行了探究,但利用数值模拟分析岩石不同加载方式下损伤演化规律的较少。选用SHPB数值模拟方式进行砂岩动态冲击试验,结合裂纹密度法建立的动损伤模型,研究其不同加载方式下的损伤演化规律,为正确认识砂岩动态破坏机理和损伤演化规律提供理论基础,促进爆破增渗技术的进一步发展。
1 数值实验模型的建立
1.1 砂岩静态试验物理力学参数
砂岩的静态物理和力学试验在石家庄铁道大学工程力学实验室进行,试件尺寸取Φ50 mm×100 mm。通过单轴抗压强度试验测得单轴抗压强度、弹性模量等力学指标[13],基本数据参考文献[13]中静态试验数据和文献[6]中的公式计算得来,且砂岩静载物理力学参数如表1所示。

表1 砂岩静载物理力学参数Table 1 Physical and mechanical parameters of sandstone under static load
1.2 有限元模型的建立
数值模拟中以LS-DYNA3D软件为基本软件进行建模,此软件可进行显式和隐式两种求解方法,其中显式计算输出的d3plot文件占存小,计算快捷,收敛效果比较好,隐式求解需要进行方程式的平衡迭代,计算复杂。因此本文模拟以显式分析为主,不考虑隐式求解。杆件和试件材料模型分别采用MAT_ELASTIC和HJC(Holmguist-Johnson-Cook)关键字进行设置,利用ANSYS计算模块进行计算。HJC模型最初用于研究混凝土极限力学特性,由于其对描述高速冲击情况良好被岩石冲击研究引用至今[14]。受试验等条件的限制,HJC模型中21个参数除基本力学参数外均参考文献[14]中数据。SHPB杆件参数如表2所示,砂岩模型参数如表3所示。
常规状态下的模型在杆底端整体模型环向为自由无约束边界;一维加载透射杆底部为点约束边界,杆件环向边界约束转动,岩石无约束,无压力施加,入射顶端为面约束边界,施加入射应力波曲线;三维加载整体杆件底端与环向为点约束边界,岩石和入射杆顶端为面约束边界,施加对应荷载曲线。

表2 SHPB杆件模型参数Table 2 Parameters of SHPB bar model
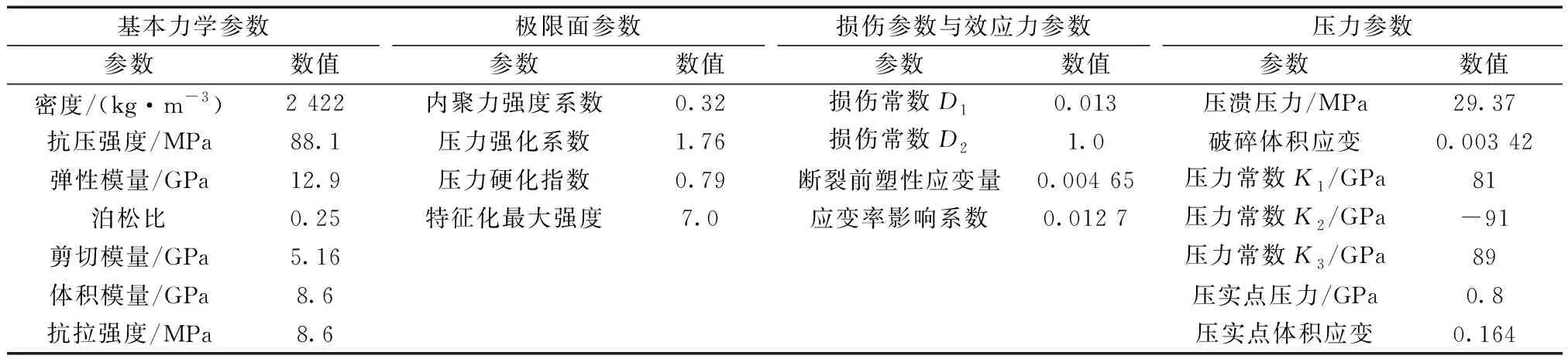
表3 砂岩HJC模型材料参数Table 3 Material parameters of sandstone HJC model
2 不同加载方式砂岩动态冲击模拟
2.1 常规动态冲击模拟
岩石SHPB数值模拟是在实验基础上进行的,为保证结果的可靠性和有效性,需要满足实验的两个基本假定条件:一维应力波原理和均匀性假定,本文模型在满足上述两个条件下建立。
模型参照霍普金森压杆试验仪构件的主要尺寸建立,其中砂岩试样尺寸选用直径50 mm,长度25 mm,杆件部分由300 mm长度子弹、3 000 mm长度入射杆和2 000 mm长度透射杆(半径均为50 mm)三部分组成。在模拟中为保证应力平衡,避免波形剧烈震荡,需要设置波形整形器。目前,整形器大多采用紫铜片,基于试验设置整形器尺寸为半径3.6 mm来进行建模,整形后的波形如图1所示。
从图1中可以看出曲线开始上升比较缓慢,波形比较平滑,无剧烈震荡效果,这样可使试件在冲击过程中达到应力平衡状态。
有限元分析包含前后处理两方面,网格划分作为前处理的重要一步,通常它的密度和划分形式对模拟数据结果影响颇大。本模型采用Solid164实体单元进行建模,考虑模型计算量和精度问题,选用映射网格划分方法进行划分,同时,为了更好地分析岩石损伤的效果,网格划分采用不同划分密度。子弹、入射杆和透射杆划分较组略且网格划分密度大致相同,其网格尺寸沿轴向为10 mm,划分结果为:子弹单元数3 151 个和节点数3 597 个;入射杆单元数31 501 个和节点数34 917 个;透射杆单元数21 001个和节点数23 317 个。试件划分较密,网格尺寸沿轴向为1.25 mm,划分结果为单元数21 301个和节点数23 017 个,砂岩试件局部放大图如图2所示。
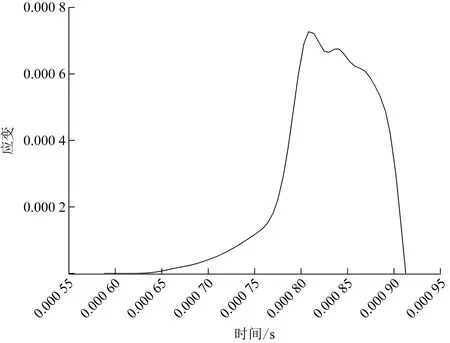
图1 波形整形图Fig.1 Waveform chart
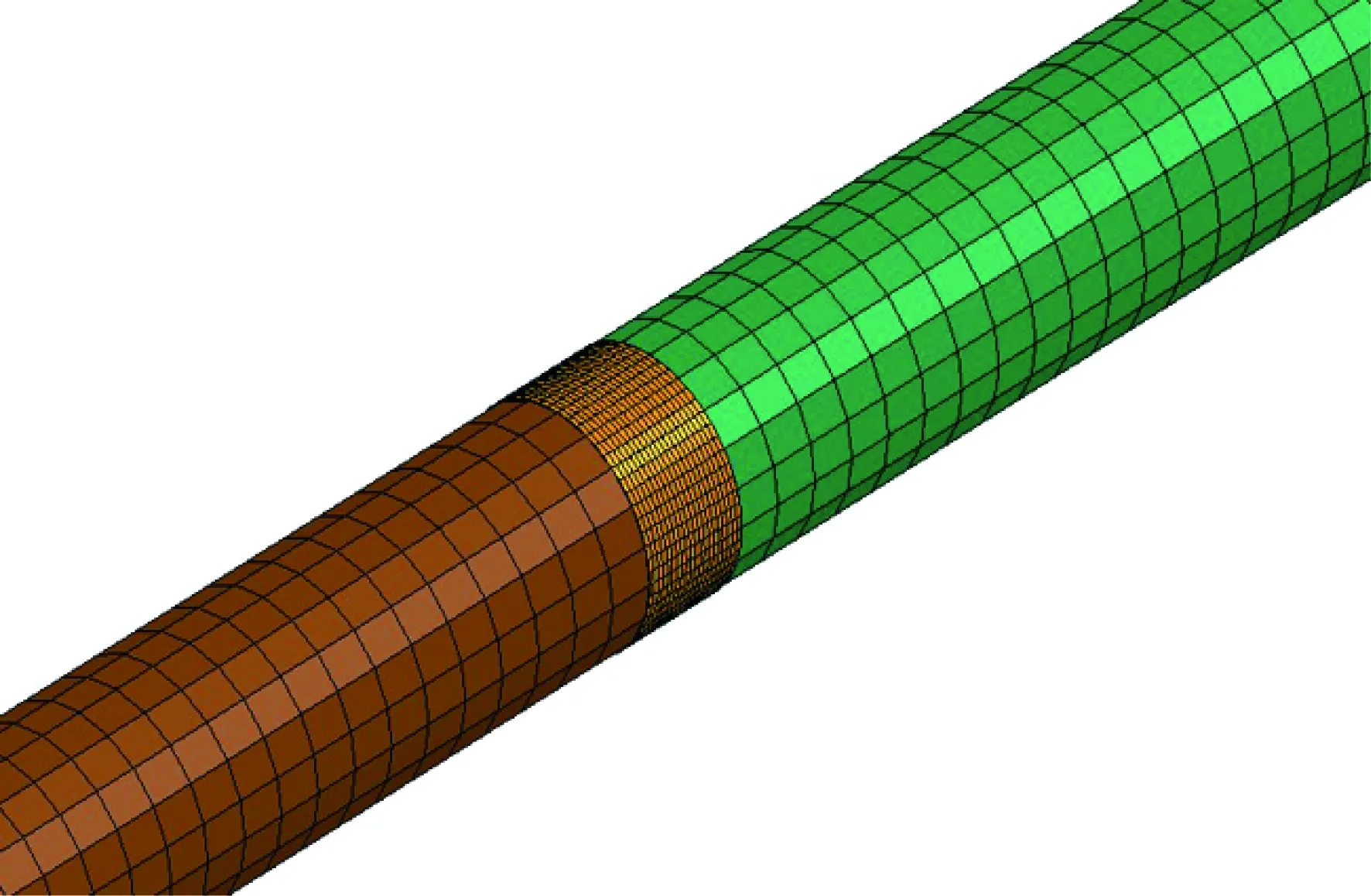
图2 模型局部放大图Fig.2 Model local magnific
在LS-DYNA软件中接触设置包括单面、双向、单向、固一4种类型,前3种接触类型的算法均采用罚函数法,固一连接接触算法不固定,一般有罚函数法、动约束法和分布参数法3种算法[15]。模型接触设置主要采用罚函数法,为了应力波更好传播以接近实际效果这一目的,全部设置成双向接触类型。子弹与杆件接触选用面面自动接触;杆件和砂岩的接触设置为侵蚀接触,设置接触主从面,砂岩面为主,两种接触其他参数默认系统设置。同时设置单元失效模拟砂岩冲击破坏,其最大失效主应变设为0.006,进而分析砂岩破坏后体积变化[16]。
2.2 轴压加载下砂岩数值模拟
轴压加载模拟对应试验的一维动静组合加载,对透射杆后端进行约束设置,入射杆前端施加预应力,模拟单向轴压作用下砂岩的损伤状况。轴压加载方法有动态松弛法和dyna文件法,LS-DYNA中为解决隐式问题引入动态松弛法,用于优先把预应力和变形考虑进去,避免应力变化过快和不收敛情况出现,与显示方式求解法不符,且dyna文件法对于隐式和显示都适用,它第一阶段进行应力初始化设置,第二阶段将dyna文件导入,其适用后续分析输入文件做大的改动[17]。
SHPB试验中只有轴压无围压时,砂岩与杆件接触的两端出现明显的端部效应,破坏形状呈锥形,端部基本无破坏,这是受界面摩擦的影响,在法向荷载和滑动速度较高时,动摩擦因数小于静摩擦因数,且仅对有轴压的试件考虑界面摩擦力[18],数值模拟则可以避免界面摩擦的影响,冲击中受力易平衡。为更好地与文献[13]中实验对应,应力初始化接触设置采用最简单的面面接触,设置静摩擦因数为0.18,动摩擦因数为0.05。
由文献[6]中提到采用入射波形式加载可以使试样在破坏前达到应力均匀,曲线震荡不明显。在模拟时考虑以常规状态模拟的入射应力与轴压值相拟合的曲线作为入射波来替代子弹撞击进行轴压加载数值模拟。模拟方案以轴压6、10、14、16 MPa,入射波速8、10、12、14、16 m/s进行20次冲击模拟,以研究不同入射波速和轴压对砂岩损伤演化规律的影响。以轴压10 MPa,入射波速8 m/s为例,入射波曲线如图3所示,入射波为半正弦波。
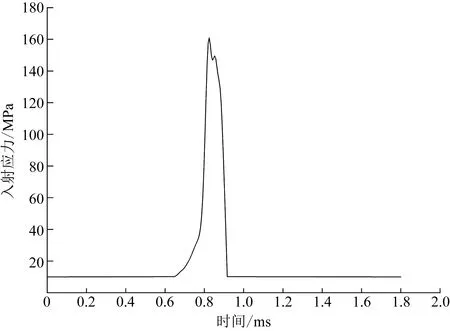
图3 入射应力波Fig.3 Incident stress wave
2.3 三维加载下砂岩数值模拟
三维加载中轴压和围压共同施加,制定6组组合模拟方案,轴压和围压分别为6、3 MPa,6、6 MPa,6、9MPa,12、3 MPa,12、6 MPa,12、9 MPa。使用dyna文件法进行模拟,对透射杆底端点约束,试件和入射杆顶端面约束,通过DEFINE_CURVE关键字定义第一步的围压和轴压曲线及第二步的围压和入射波曲线,并利用关键字LOAD_SEGMENT_SET导入先前所设置的曲线。
三维模拟为达到与试验加载高度相似,以轴向压力与速度波拟合曲线作为入射波施加于入射杆顶端,围压只施加于试样部分。总共进行30次模拟,以考虑相同轴压不同围压和相同围压不同轴压时砂岩的损伤破坏规律。同时,研究冲击速度、轴压和围压三者组合下对岩石破坏的影响。
3 砂岩损伤演化规律分析
3.1 损伤模型
砂岩损伤演化规律研究以损伤变量作为基础进行,损伤变量是表征结构内部劣化程度的量化参数[19]。损伤变量的定义形式有多种,以往研究中常采用弹性模量法和能量耗散法,其公式为
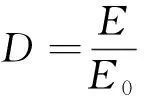
(1)

(2)
式中:D为损伤变量;E0和E表示岩石损伤前后的动态弹性模量;en和esum表示岩石第n次试验的消耗能和试验全过程耗能总和。
以上两种常规方法试验和计算比较复杂,同时会使损伤数值偏大,不适用于数值模拟。根据损伤变量定义特点,岩石损伤表征分为宏观和微观两方面,宏观损伤分析多以声波波速法为主,多用于实验,在数值模拟研究中适用以岩石各向同性为前提,大量裂纹混合,不考虑单裂隙情况,基于裂纹密度构建损伤变量[20]。由岩石的孔隙率表征岩石的损伤变量,定义为岩石的裂纹密度,公式为

(3)
式(3)中:Vn为砂岩冲击模拟前体积;V为砂岩冲击模拟后失效单元体积变化量。
3.2 损伤演化特性分析
从损伤模型中可以得出,损伤变量和冲击前后的体积变化量相关,不同冲击速度造成岩石不同程度损伤,损伤度用损伤变量来表征。裂纹密度法以体积变化为基础进行损伤表征,模拟中体积改变是通过失效单元关键字MAT_ADD_EROSION进行控制,利用LS-DYNA软件中Measure功能得到岩石微小体积改变量,将岩石体积改变量与其初始体积相比,得到最终的裂纹密度。无轴压和围压作用下冲击速度与裂纹密度关系如图4所示。从图4中可以得出,裂纹密度随着冲击速度的增加呈线性上升趋势,表明砂岩的损伤破坏程度与冲击波的大小密切相关。
在深部开采工程中,地应力状态研究越来越重要,地应力通常是由地层土压力和地质运动产生的构造应力组成,对其简化后只考虑土层应力进行一维轴向压力数值模拟。岩石轴压加载数值模拟过程中不同冲击速度与损伤关系如图5所示,以冲击速度为12 m/s为例,不同轴压与损伤的关系如图6所示。从图5中可以看出,砂岩的损伤和冲击速度仍呈正相关,随着冲击速度的增大,砂岩损伤逐渐增大,相同速度轴压值越大,曲线越靠下,裂纹密度越小。从图6中看出,随着轴压的增加,裂纹密度呈下降趋势。
模拟中以某一时刻的孔隙体积为基础进行裂纹密度分析,由于常规状态与轴压加载状态所建模型PART组成不同,单元划分不同,所取破坏点时刻出现差异,导致出现图4比图5数值偏小现象,而且轴压加载模拟中考虑的入射应力波直接加载处于更为理想状态下进行的,与试验中子弹撞击模式有所出入,但在同一加载方式下,轴压的增长又使损伤度降低。说明一端约束,一端施加动静组合入射波曲线在一定程度上达到了试验效果,同时验证了轴压作用下岩石初始损伤速率增长缓慢,轴压对岩石的初始破坏速率具有一定抑制作用。从微观角度看,由于轴压存在控制了岩石内部微裂纹的扩展,才会减缓损伤速率。
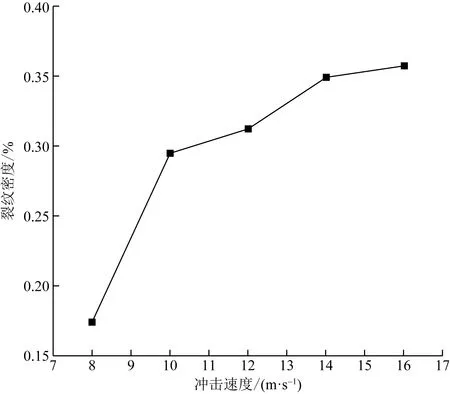
图4 常规冲击模拟损伤演化Fig.4 Damage evolution of conventional impact simulation

图5 不同轴压下冲击速度与裂纹密度关系Fig.5 Relationship between impact velocity and crack density under different axial compression
为满足实际工程的需要,进行三维加载条件下的模拟,从两方面考虑。第一是相同围压不同轴压下岩石冲击速度与损伤的关系,取围压为6 MPa,不同轴压冲击速度与损伤关系如图7所示,从图7中可以看出,轴压大小对岩石损伤影响颇大,说明轴压越小,损伤越大,曲线越靠上,这和只有轴压时的情况类似。第二是轴压固定,围压不同时岩石冲击速度与损伤关系,为了更好地分析取轴压为6 MPa,不同围压冲击速度与损伤关系如图8所示,从图8中可以得到,围压6 MPa比围压3 MPa损伤更为严重,而围9 MPa比围压6 MPa损伤降低,围压值超过轴压值时,损伤减小。因三维加载入射应力波和围压曲线进行分开加载,当围压值小于轴压值时,岩石所受的围压静载未起到抑制作用,反而增加了岩石的环向应变,导致损伤增大。

图6 不同轴压与裂纹密度关系Fig.6 Relationship between different axial compression and crack density
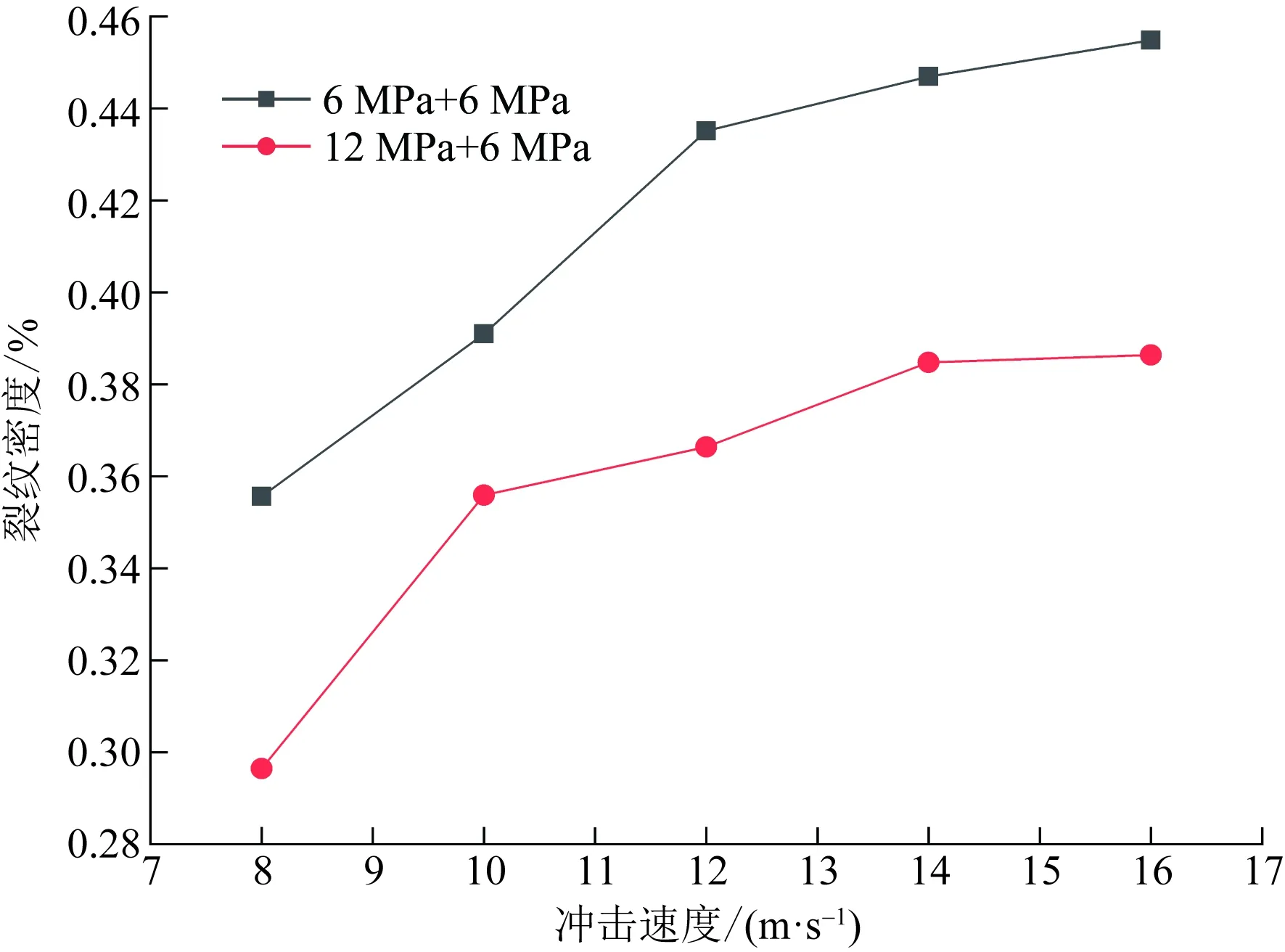
图7 相同围压不同轴压与裂纹密度关系Fig.7 Relationship between crack density and different axial compression under the same confining pressure

图8 不同围压与裂纹密度关系Fig.8 Relationship between crack density and confining pressure
4 结论
采用LS-DYNA软件进行不同加载方式下砂岩冲击实验数值模拟,并结合损伤模型计算岩石损伤,通过岩石损伤演化规律进行分析,得出以下结论。
(1)波形整形器设置可以有效解决冲击实验模拟中波形图震荡问题;在轴压和围压加载模拟第一步中采用最为简单的面面自动接触,可以保证模拟的接触设置更有效,第二步设置为侵蚀接触,方便分析岩石的体积改变,进而研究砂岩的损伤。
(2)利用dyna文件法分两段对进行模拟,先进行应力初始化,再导入下一段模拟可以有效避免计算不收敛情况出现,只有轴压存在时,轴压固定砂岩损伤随冲击速度增加而上升,但初始增长速率缓慢,说明轴压对岩石的裂纹扩展具有抑制作用。
(3)在常规状态下砂岩损伤变量随着冲击速度增大而增大;围压和冲击速度不变时,轴压对岩石损伤的影响与单独轴压加载情况类似;轴压和冲击速度均不变时,围压增加损伤减小(围压值大于等于轴压值),说明围压可以有效控制岩石微裂纹的扩展。
