基于RBF 神经网络的固定时间控制器设计

张雯雯

（河南理工大学 河南省焦作市 454003）

反步法是一种递归形式的控制方法，在许多工程领域有广泛的应用。Hedrick 等人率先在反步法中引进低通滤波器解决反步法中因虚拟控制律多次求导引起的“计算爆炸”问题，这种引入低阶滤波器的方法称为动态面控制（DSC）。文献利用DSC 技术解决了“计算爆炸”问题，证明系统半全局稳定。文献将DSC 方法用于状态观测器的设计中，基于李雅普诺夫方法证明系统稳定性和信号有界性。文献构造李雅普诺夫函数时引入滤波器的估计误差，证明跟踪误差收敛到一定范围内。文献针对具有未知有界扰动的非线性系统，提出了自适应动态面控制。

RBF 神经网络因网络结构简单、能以任意精度逼近任何单值连续函数等优点，在机器人、无人机等控制系统设计中得到广泛应用。文献将动态面与RBF 网络自适应控制相结合，保证不确定严格反馈非线性系统的闭环系统误差收敛到一个小邻域内，但上述文献均为指数稳定或者渐近稳定。在系统稳定的前提下，有限时间控制由于具有收敛速度快、跟踪精度高等优点被广泛应用，但有限时间收敛时间上界过于依赖系统初始状态，一旦远离平衡点，收敛时间将趋于无穷。

针对上述问题，本文针对一类不确定的严格反馈非线性系统，提出一种固定时间收敛动态面控制器设计方法，有效解决了反步法中因虚拟控制反复求导引起的“计算爆炸”问题。

1 问题描述及预备知识

1.1 问题描述

1.2 预备知识

对于如下系统：

2 基于RBF神经网络的控制器设计及稳定性分析

2.1 滤波器设计

2.2 自适应律设计

2.3 控制器设计

图1： 跟踪误差z1

2.4 稳定性分析

3 仿真实例

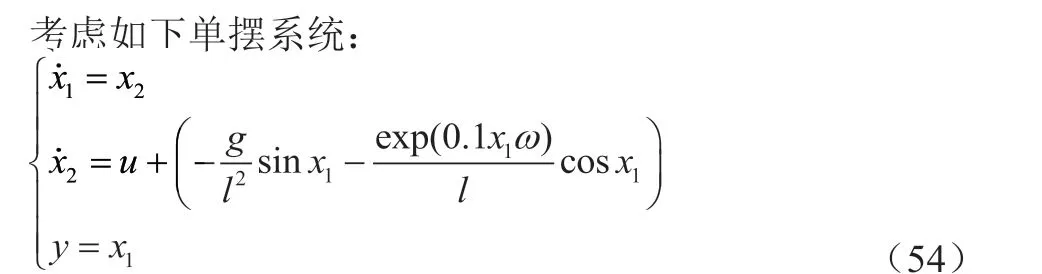
其中x,x分别为单摆偏离平衡位置的角度和速度，y 是输出，u 是控制量，g 为重力加速度，l 为单摆摆长，ω 为未知参数， ，ω=1，初始状态 ，控制目标是使单摆偏离平衡位置的角度跟踪参考信号，设参考信号为 ，RBF 神经网络高斯基函数中心点的坐标矢量c=[-2 -1 0 1 2]，高斯基函数的宽度为b=3，神经网络初始权值设为θ(0)=[0 0 0 0 0]，仿真总时长为30 秒（s），控制器相关参数选取如下：g=9.8m/s，l=5m，k=1，k=0.1，k=8，k=0.1，φ=0.3，φ=0.2，l=0.05，η=0.0025，l=1，v=0.02，ξ=ξ=30。

仿真结果如图所示，图2 为系统的跟踪误差z轨迹，由图可以看出，采用RBF 神经网络，系统输出能快速的跟踪参考信号，且收敛时间更快跟踪误差更小，速度更快。

图2： 神经网络权值的欧几里得范数

仿真验证中一阶滤波器为： ，，w为 经过滤波时间v得到。图2 和图3 分别为在初值为x(0)=[0.2 0.1]，x(0)=[0.5 -0.5]，x(0)=[1 0]下神经网络权值的欧几里得范数变化图和滤波误差e图像。在不同初值情况下，由图2 可看出权值的欧几里得范数在固定时间内收敛到一个紧集内。由图3 可看出本文所提出的固定时间滤波器比传统的低阶滤波器精度更高。综上，本文所提的方案可有效用于单摆等严格反馈非线性系统，满足快速性和高精度的任务需求。

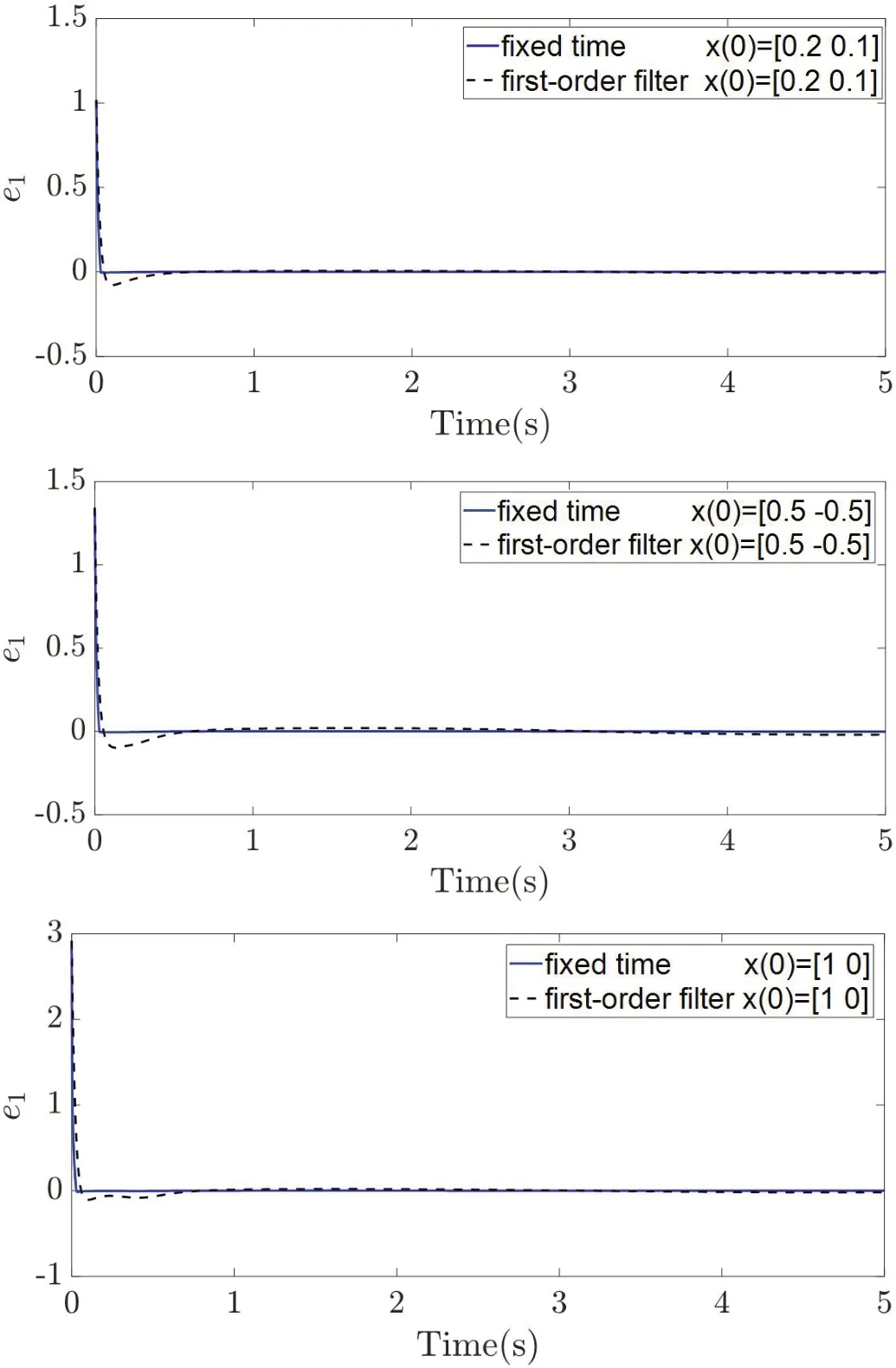
图3： 滤波误差

4 结论

本文针对一类具有不确定的严格反馈非线性系统，提出了基于RBF 神经网络的固定时间控制器设计方案。通过定义合适的李雅普诺夫函数证明了系统的稳定性，采用固定时间滤波器解决了反步法中“参数爆炸”的问题，简化计算减小了计算量。仿真结果表明，本文所提方案在相同增益下具有收敛速度快、跟踪精度高、易于工程实现的优点。